Квадратные корни. Арифметический квадратный корень
Конспект урока по алгебре
в 8 классе
«Квадратные корни.
Арифметический квадратный корень»
Тема: «Квадратные корни. Арифметический квадратный корень».
Цели: ввести понятия квадратного корня и арифметического квадратного корня; сформировать умение извлекать квадратные корни; развивать логическое мышление, смекалку.
Оборудование: тучи (2 шт.), звезды(2 шт.), ленто (2 шт.), флаг(2 шт.), прямоугольники (2 шт.)
Тип урока: Урок изучения нового материала
План урока:
I – Организационный момент
II – Актуализация знаний
III – Изучение нового материала
IV – Первичное закрепление знаний
V – Подведение итогов занятия. Рефлексия
VI – Домашнее задание
.
Ход урока:
- Организационный момент.
- Здравствуйте, дети! Проверьте, все ли, что нужно к уроку лежит у вас на партах? (тетрадь, ручка, дневник, сборник задач)
- Садитесь!
- Актуализация знаний
- Дети, сейчас вам нужно будет решить примеры, ответы к которым являются ключом к оглашению темы нашего урока. Данил выходит к доске и будет складывать части ответов-слов, которые остальные учащиеся будут решать на местах и нам говорить ответ.
Например, задание: 62
 Ответ: 36. Ищем этот ответ среди всех ответов, написанных на листках и складываем по-порядку – получим первый слог с названия нашей темы.
Ответ: 36. Ищем этот ответ среди всех ответов, написанных на листках и складываем по-порядку – получим первый слог с названия нашей темы.
- Когда решим все примеры, мы узнаем тему нашего сегодняшнего урока.





Задания:
-
 62 (36)
62 (36)
-
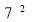 (49);
(49);
- 22 (4)
-
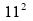 (121);
(121);
-

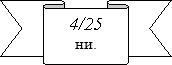
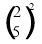 (4/25);
(4/25);
-
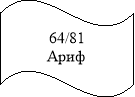
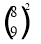 (64/81);
(64/81);
-
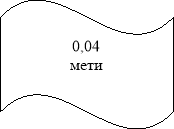
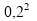 (0,04);
(0,04);
-
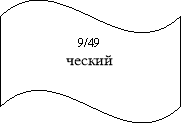
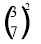 (9/49);
(9/49);
-
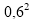 (0,36).
(0,36).
- 42 (16)
- 82 (64)
- 52 (25)
-Правильно! Тема нашего урока звучит именно так: «Квадратные корни. Арифметический квадратный корень».
I. Изучение нового материала
- Введение понятия квадратного корня.
- Рассмотрим задачу о нахождении стороны квадрата по его площади.
Пусть площадь квадрата равна 64 см2. Чему равна длина стороны этого квадрата? (8 см)
- А если площадь квадрата равна 49 см2? 81 см2 ? 121 см2 ?(7 см, 9см, 11 см)
- Теперь давайте попробуем решить задачу по-другому. Обозначим длину стороны квадрата (в сантиметрах) буквой х.
- Тогда как запишется площадь квадрата через х? (х2 см2)
- Правильно, будет х2 см2. По условию площадь равна 64 см², значит, что мы имеем из этого?(х²=64).
-Какие числа являются корнями уравнения х²=64? (число 8)
- И только? ( и число -8)
- Действительно, 8²=64 и (-8)²=64. Так как длина не может выражаться отрицательным числом, то условию задачи удовлетворяет только один из корней, какой? (число 8).
- Итак, длина стороны квадрата равна 8 см.
Корни уравнения х²=64, т.е. числа, квадраты которых равны 64, называют квадратными корнями из числа 64.
Задание. Вместо пустых клеточек поставьте числа так, чтобы равенства были верными:
2 =16 (4,-4) ²=1/9 (1/3,-1/3) ²=100 (10,-10)
- Теперь попробуйте сами сформулировать определение квадратного корня.
- Правильно! Квадратным корнем из числа а называют число, квадрат которого равен а.
- Открыли все тетради, записали число, классная работа. Тема урока: Квадратные корни. Арифметический квадратный корень. Записываем и выделяем определение.
Определение. Квадратным корнем из числа а называют число, квадрат которого равен а.
Задание: скажите, является ли число n квадратным корнем из числа m, и как это проверить, если:
а) n=5, m=25; (52=25) в) n=0,3, m=0,9;
б) n= - 7, m=49; г) n=6, m= - 36.
- Введение понятия арифметического квадратного корня.
- Ребята, в свою очередь арифметический квадратный корень из числа а называют неотрицательное число, квадрат которого равен а.
Арифметический квадратный корень из числа а означают √а. Знак √ называют знаком квадратного корня или радикалом.
- С этого следует, что равенство ![]() означает одновременно выполнение двух условий: b²=a и b≥0.
означает одновременно выполнение двух условий: b²=a и b≥0.
- Рассмотрим на выше приведенном примере. Какое число является неотрицательным корнем уравнения х²=64?
- То есть, что называют арифметическим квадратным корнем из 64? (Число 8 — неотрицательный корень уравнения х²=64 — называют арифметическим квадратным корнем из 64. )
- Иначе говоря, арифметический квадратный корень из 64 — это неотрицательное число, квадрат которого равен 64.
- Попробуйте сформулировать определение арифметического квадратного корня сами.
- Запишем определение в тетради.
Определение. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
- Запишите и выделите то, что если b²=a и b≥0, то √а=b.
Для какого-либо неотрицательного числа а справедливо, что √а≥0 и (√а)2=а. Например: (√4)2=4, (√2)2=2
- Обратите внимание, что выражение, которое стоит под знаком радикала, называют подкоренным выражением.
Действие нахождения арифметического квадратного корня из числа называют извлечения квадратного корня.
Задание: определите, является ли число n арифметическим квадратным корнем из числа m, если:
а) n=8, m=64; в) n=0,2, m=0,4;
б) n= - 3, m=9; г) n=0,4, m=0,16.
Физкультминутка. Гимнастика для глаз: быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5 (повторить 4–5 раз).
3.Основное свойство арифметического квадратного корня.
Вычислите значения следующих выражений:
![]() ,
, ![]() ,
, 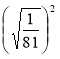 .
.
- Какой вывод из этого можно сделать?
![]() , если а≥0
, если а≥0
IV . Первичное закрепление знаний
-Найдите значение арифметического квадратного корня:
а) ![]() (7); б)
(7); б) ![]() (1/4); в)
(1/4); в) ![]() (90); г)
(90); г) ![]() (1/5); д)
(1/5); д) ![]() (0,3); е)
(0,3); е) ![]() (2/3√5).
(2/3√5).
- Найдите значение выражения:
а) ![]() (2/5); б)
(2/5); б) ![]() (); в)
(); в) 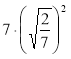 ; г)
; г) ![]() .
.
3. “Найди ошибку”

4.Укажите натуральные значения n, при которых является натуральным числом значение выражения ![]()
(Решение: чтобы значение выражения ![]() являлось натуральным числом, подкоренное выражение должно быть равно 1, 4 или 9. Получаем 3 случая:
являлось натуральным числом, подкоренное выражение должно быть равно 1, 4 или 9. Получаем 3 случая:
11 — n=1 11 — n=4 11 — n=9
n=10 n=7 n=2
Эти же значения можно было найти подбором.
Ответ: 2, 7, 10.)
- Очень хорошо
V Подведение итогов занятия.
Что называется квадратным корнем из числа а?
- Сколько квадратных корней может быть из числа а?
- Что такое арифметический квадратный корень из числа а?
-
Имеет ли смысл запись
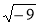 ? Почему?
? Почему?
- Молодцы ребята! Сегодня вы очень хорошо поработали. Поэтому получаете такие оценки…
VI Домашнее задание
Найдите значение выражения:
а) ![]() ; б)
; б) 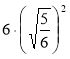 ; в)
; в) ![]() .
.
Из сборников ст.47, номера 68, 69, 70,71


про публікацію авторської розробки
Додати розробку
