Конспект урока по алгебре в 8 классе «Свойства корня»
Конспект урока по алгебре
в 8 классе
«Свойства корня»
Цели: Изучить свойства квадратных корней, научиться применять данные свойства в вычислениях, способствовать развитию устной речи учащихся (умение владеть предметным языком) , способствовать формированию толерантного отношения к себе, одноклассникам, учителю, поддерживать интерес к изучаемому предмету.
Оборудование: примеры на доске (на А4), девиз урока.
Тип урока: урок изучения новой темы
Ход урока
I этап. Организационный.
Здравствуйте, дети! Проверьте, все ли, что нужно к уроку лежит у вас на партах? (тетрадь, ручка, дневник, сборник задач)
- Садитесь!
-Сегодня нам предстоит изучить свойства квадратного корня. Какие знания и умения будут сегодня нам необходимы? (знание определения арифметического квадратного корня, умение извлекать квадратный корень, умение работать с таблицей квадратов двузначных чисел)
- Давайте повторим материал, который нам сегодня будет необходим.
II этап. Актуализация опорных знаний.
- Дайте определение арифметического квадратного корня.
- Ребята, сейчас вам нужно будет решить примеры, которые написаны на доске. Ваше задание молча выйти и выбрать себе пример, ответ к которому ты знаешь. После чего, передаете эстафету следующему ученику класса на выбор. Только главное условие: НИКТО НЕ ГОВОРИТ!!!
А.
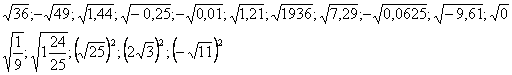
В. ![]()
III этап. Изучение новой темы. Метод проблемного обучения
Ребята, сей час вам нужно самостоятельно решить два примера различными способами и из них выбрать оптимальный вариант решений, обосновать свой выбор. (Один ученик возле доски)
1) Вычислите: ![]()
Выбор оптимального способа решения
1 вариант вычисления: ![]()
2 вариант вычисления: ![]()
- Какой способ удобней и быстрее?
- Таким образом, мы с вами вывели и доказали 1 свойство квадратных корней, который называется свойство квадратного корня из произведения.
В конспект
|
Свойства квадратного корня:
Пример:
|
- Для понимания, усвоения и закрепления данного свойства устно выполним следующее упражнение.
Первичное закрепление. Вычислите: 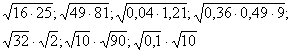
- Обратите внимание, что данное свойство можно применять как слева направо, так и справа налево.
2) Вычислите: ![]()
1 вариант вычисления: ![]()
2 вариант вычисления: ![]()
- Какой способ удобней и быстрее?
- Это второе свойство квадратных корней и называется оно свойство квадратного корня из дроби.
В конспект
|
Свойства квадратного корня:
1)
Пример:
Пример:
|
- С помощью данного свойства вычислите:
Первичное закрепление. Вычислите 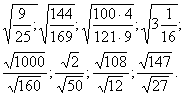
- Здесь также обратите внимание на то, что данное свойство можно применять как слева направо, так и справа налево
- Как вынести множитель из-под корня?
- Разложить подкоренное выражение на множители и извлечь корни, которые извлекаются. Смотрим:
![]() =
= ![]() = 6
= 6![]()
- Как видим, всё получилось. Это, кстати, не самый быстрый, но самый надёжный способ. Раскладывать число на самые маленькие множители, а затем собирать в кучки одинаковые. Способ успешно применяется и при перемножении неудобных корней.
|
Свойства квадратного корня:
1)
Пример:
Пример:
Пример: |
- Например, надо вычислить: ![]() *
*![]() *
*![]() =
= ![]() =
= ![]() =2*3*3*6 = 108
=2*3*3*6 = 108
- Вот и всё. Конечно, раскладывать до упора не обязательно. Всё определяется вашими личными способностями. Довели пример до состояния, когда вам всё ясно, значит, можно уже считать. Главное - не ошибаться. Не человек для математики, а математика для человека!
- Как внести число под корень, как вы думаете?
Предположим, что у нас есть вот такое выражение: 2![]()
- Можно ли спрятать двойку внутрь корня?
- Хорошо! Если из двойки сделать корень, сработает формула умножения корней. А как из двойки корень сделать?
- Правильно! Двойка - это корень квадратный из четырёх!
Вот и пишем: 2![]() =
= ![]() *
*![]() =
=![]()
- Какой вывод можно сделать?
-Любое неотрицательное число, умноженное на корень, можно внести под корень. Но - не забывайте! - под корнем это число станет квадратом самого себя. Это действие - внесение числа под корень - можно ещё назвать умножением числа на корень.
В конспект
|
Свойства квадратного корня:
1)
Пример:
Пример:
Пример:
Пример: 4 |
IV этап. Закрепление изученного материала.
-
Вычислите
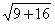
- Можно ли в данном случае применить свойство квадратного корня из произведения. Проверить практически.
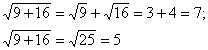
Вывод о том, что свойства квадратных корней существуют только для произведения и деления квадратных корней (возведения в степень квадратных корней), должны сформулировать учащиеся
2)Вычислите: ![]() (возле доски)
(возле доски)
- Среди всех возможных способов решения выберите подходящие и правильные.
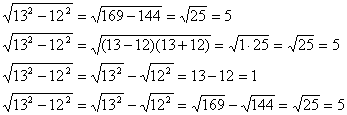
Вывод: свойства квадратных корней имеются только для умножения и деления
- Вычислите, используя свойство квадратного корня из произведения:

- Молодцы!
V этап. Домашнее задание:
Страница 21 из сборников №№80, 81,82, 83

про публікацію авторської розробки
Додати розробку
