Урок алгебры в 8 классе по теме «Уравнение х2 = а»

Конспект урока по алгебре
в 8 классе
«Квадратные корни.

Арифметический квадратный корень»

Урок алгебры в 8 классе по теме «Уравнение х² = а»

Цели:

рассмотреть решение простейшего квадратного уравнения х²=а; формировать навык решения такого вида уравнений; содействовать развитию у школьников логического мышления, культуры  математической речи, памяти; содействовать формированию у учащихся чувства ответственности за собственную и коллективную деятельность, содействовать осознанию учащимися ценности изучаемого предмета.

Оборудование: карточки с примерами, кроткий конспект, листочки для опроса.

Тип урока. Урок изучения новых знаний и способов действий.

Ход урока

1. Организационный момент.

- Здравствуйте, дети! Проверьте, все ли, что нужно к уроку лежит у вас на партах? (тетрадь, ручка, дневник, сборник задач)

- Садитесь!

II. Постановка цели урока. Мотивация.

•                   Ребята, восточная мудрость гласит: «Можно коня привести к воде, но нельзя заставить его пить». И человека невозможно заставить учиться хорошо, если он сам не старается узнать больше, не имеет желания работать над своим умственным развитием. Ведь знания только тогда знания, когда они приобретены усилиями своей мысли, а не одной памятью.

Сегодня у нас урок по теме «Уравнение х² = а». Мы познакомимся с простейшим квадратным уравнением х² = а. Научимся решать такого вида уравнения.

III. Актуализация субъектного опыта.

1. Проверка домашнего задания.

№68, №69- устно

№ 70(1-3) –  1 ученик пишет на доске;

№ 70 (4 - 6) – 2 -й ученик на доске;

№ 71(4 - 6) – 3- й ученик на доске;

№ 71(1-3) – комментирование с места.

2) Чтобы успешно работать практически, нужно знать теоретический материал. Проверим ваши знания.

•                   Дайте определение квадратного корня.
•                   Определение арифметического квадратного корня.
•                   При каких условиях 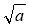= b?
•                   Хорошо! 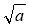= b: а≥0, b≥0 и  b²=а (Написать на доске)
•                   Для каких значений а выражение 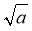имеет смысл?
•                   Правильно, для а≥0. А почему?
•                   Да потому, что число во второй и парной степени вообще, не может быть отрицательным. Поскольку, b²=а, то следует, что: а≥0.
•                   Открыли тетради, записали число, классная работа. Тема нашего урока - Уравнение х² = а.  Запишите себе  с доски:

В конспект

3) Имеет ли смысл выражение: (Пишу на доске, дети в тетрадях)

  (Да)

 (Да)

  (нет)

           (Да)

 4) – Ребята, обратите внимание, если ()²=а, а≥0, то чему равно =?  

В конспект

- Запишите себе такую табличку.

5) На обратной стороне доски будут написаны примеры.

- Ребята, сейчас вам нужно будет решить примеры, которые написаны на доске. Ваше задание молча выйти и выбрать себе пример, ответ к которому ты знаешь. После чего, передаете эстафету следующему ученику класса на выбор. Только главное условие: НИКТО НЕ ГОВОРИТ!!!

Вычислите:     .

IV.  Изучение нового материала (Организация восприятия, осмысления и пер­вичного запоминания нового учебного материала)

- Рассмотрим х² = а где а – произвольное число) - это уравнение квадратное. В зависимости от числа а при решении этого уравнения возможен один из трех случаев.

1. Если 0, то данное уравнение корней не имеет. Действительно, для любого числа х левая часть уравнения х² 0, а правая часть – число

а 0. Получаем противоречие: неотрицательная величина не может равняться отрицательному числу.

2. Если а = 0, то уравнение имеет единственный корень, равный нулю (т. е. х = 0). Только для числа х = 0 уравнение х² = 0 обращается в верное равенство.

3. Если 0, то уравнение имеет два корня х₁ = и х₂ = . Действительно, при подстановке в данное уравнение числа  получаем: ² = (-1)² ∙ = 1 ∙ а = а (верное равенство), при подстановке значения

имеем: (также верное равенство).

 В конспект

- х²=5:  х₁=   и   х₂= - – Эти корни являются иррациональными числами, т. к. не существует рационального числа, квадрат которого равен 5.

- Посчитайте на калькуляторе, чему равен ; ;

- Какую особенность вы видите?

- Иррациональное число представлено в виде бесконечной непериодической десятичной дроби. Поэтому, какое определение иррациональных чисел можно сформулировать?

 Правильно! Иррациональное число – это число представлено в виде бесконечной непериодической десятичной дроби.

- Запишите себе в тетради.

В конспект

6) Решим уравнение (х -2)² = 6,25.

Обозначим буквой  z величину х – 2 (т. е.  z = х – 2) и получим простейшее квадратное уравнение z² = 6,25. Это уравнение имеет два корня:

z ₁ = = - 2,5 и z₂ = = 2,5. Теперь вернемся к старой неизвестной х и получим два линейных уравнения: х – 2 = - 2,5 (его корень х₁ = - 0,5) и х – 2 = 2,5 (его корень х₂ = 4,5). Итак, данное уравнение имеет два корня х₁ = - 0,5 и х₂ = 4,5.

  V. Первичная проверка правильности понимания нового учебного материала. Организация первичного закрепления н.у.м.

Контрольный вопрос. Каковы возможные случаи решения уравнения х² = а?

№ 73(устно).

№№ 74, 75. Резерв. №76

VIII. Итоги урока

•                   Что нового вы узнали сегодня на уроке?

Надеюсь, что этот материал вы не забудете, он обязательно пригодится вам при дальнейшем изучении математики. Помните слова французского инженера-физика М. Лауэ: «Образование есть то, что остается, когда все выученное уже забыто».

•                   Оцените степень усвоения материала:
  • Усвоил полностью, могу применять;
  • Усвоил, но затрудняюсь в применении;
  • Усвоил частично;
  • Не усвоил.

IX. Информация о домашнем задании.

Выполнить задания на карточке (решить 10 уравнений).

Приложение

---------------------------------------------------------------------------------------------------------------------

Самостоятельная работа по теме «Уравнение х² = а»            Вариант 1

1) х² = 4;   2)  х² = 0,09;   3)  х² = -9;   4)  х² = 17;   5) 2х² = 0,08;   6) х² – 9 = 0;  

7) - 1 = 0;    8) (2х – 5)(2х + 5) = 75;     9) (х – 9)² = 49;      10) (х + 5)² = 2.

--------------------------------------------------------------------------------------------------------------------

Самостоятельная работа по теме «Уравнение х² = а»           Вариант 2

1) х² = 100;   2)  х² = 0,25;   3)  х² = -16;   4)  х² = 13;   5) 3х² = 0,48;   6) х² – 49 = 0;  

7) - 1 = 0;    8) (3х – 2)(3х + 2) = 5;     9) (х + 1)² = 64;      10) (х - 3)² = 3.

--------------------------------------------------------------------------------------------------------------------