Лекція по темі "Основні поняття статики"
![]()
ВСП «Немішаївський фаховий коледж НУБіП України»
Лекція
з дисципліни
«Технічної механіки»
Тема: «Основні поняття та аксіоми статики»
Для студентів спеціальності
208 «Агроінженерія» ІІ курсу денної форми навчання
Викладач: Лоїк О.А.
Немішаєве 2021
Основні поняття та аксіоми статики
План заняття
- Предмет статики.
- Матеріальна точка, абсолютне тверде тіло.
- Сила, система сил. Рівнодійна сила.
- Аксіоми статики.
- Вільне і невільне тіло.
- В'язь, реакція в'язі.
Механіка – це наука про механічний рух та механічні взаємодії. Механічний рух – це зміна взаємного розташування тіл або їхніх частин у просторі з часом. Механічні взаємодії – це матеріальні зв'язки між тілами, які ведуть до зміни механічного руху тіл або до їх деформації.
У теоретичній механіці розгляд задач ґрунтується на застосуванні математичних методів до розв'язування рівнянь, складених на основі законів і принципів механіки. Об'єктами вивчення теоретичної механіки є не самі реальні тіла, а їхні моделі, які називають матеріальною точкою (називають будь-яке макроскопічне тіло, розмірами якого за умовою даної задачі можна нехтувати), системою матеріальних точок (називають сукупність матеріальних точок, які взаємодіють між собою), абсолютно твердим тілом або твердим тілом (називають макроскопічне тіло, деформацією якого за умовами даної задачі можна нехтувати).Застосування цих моделей дають можливість зосередити дослідження на з'ясуванні основних законів механічного руху та механічних взаємодій матеріальних тіл.
У теоретичній механіці простір і час вважаються абсолютними. Простір є однорідним, ізотропним й тривимірним. Час протікає рівномірно завжди і всюди, тобто він є неперервно зростаючою скалярною величиною, що виконує роль незалежної змінної.

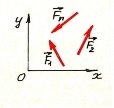
Рівновагою твердого тіла називають стан його спокою або рівномірного прямолінійного руху відносно умовно нерухомої системи відліку. Стан рівноваги твердого тіла залежить від характеру взаємодії цього тіла з іншими тілами. Величина, яка є кількісною мірою механічної взаємодії матеріальних тіл, називається силою. Сила є векторною величиною. Вона характеризується напрямом або лінією дії (під напрямом сили розуміють напрям руху, який дістало б вільне тіло, що перебуває у спокої, якби на нього подіяла ця сила), числовим значенням або модулем і точкою прикладання (матеріальна частина тіла, на яку діє сила). Графічно сила зображується відрізком прямої, довжина якого в певному масштабі дорівнює модулю сили (рис. 1.1). Числове значення (модуль) или вимірюється в ньютонах.
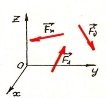
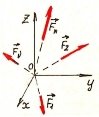
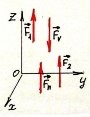
Силу, як векторну величину, можна подати через її складові або проекції на координатні осі (рис. 1.2).
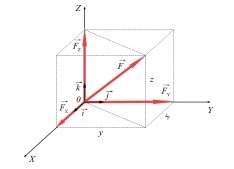
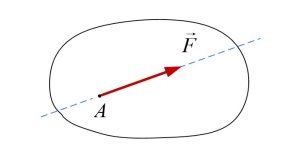
Рис. 1.1. Сила F⃗, що
прикладена до тіла в точці А Рис. 1.2. Просторове зображення
вектора сили F⃗
|
Сукупність сил, які діють на дане тверде тіло, називають системою сил (F1,F2,..., Fn ) |
|
Система сил, лінії дії яких лежать в одній площині, називається плоскою |
|
Якщо лінії дії сил лежать у різних площинах, то таку систему називають просторовою |
|
Система сил, лінії дії яких перетинаються в одній точці, називається збіжною |
|
Якщо лінії дії сил паралельні між собою, то таку систему називають системою паралельних сил
|
Якщо під час дії системи сил вільне тверде тіло не змінює свого руху або залишається в стані спокою, то така система сил називається зрівноваженою (F1,…,Fn0). Зрівноважена сила дорівнює за модулем і протилежна за напрямком до рівнодійної сили R. Сили такої системи взаємно компенсують одна одну.
Якщо, не порушуючи стану тіла, одну систему сил можна замінити іншою системою сил й навпаки, то таки системи сил називаються еквівалентними. Позначається ” ”. (F1,F2,..., Fn)(Q1,Q2,...,Qn).
У випадку, коли дія системи сил еквівалентна дії однієї силі, то таку силу називають рівнодійною (R) даної системи сил. (F1....Fn) R. Виявляється, що не всяка система сил має рівнодійну.
Сили, які діють на дане тіло з боку інших тіл, називаються зовнішніми.
Сили взаємодії між частинками даного тіла називаються внутрішніми.
Таким чином, тверде тіло перебуває в стані рівноваги тоді, коли діюча на нього зрівноважена система сил еквівалентна нулю.
За характером прикладання сили поділяють на зосереджені та розподілені. Зосереджені сили – це сили, що передаються на тіло через нескінченно малі елементи площі тобто вважається, що вони прикладені до тіла в певній точці. Зосереджена сила є абстракцією, тому що будь-яка реальна взаємодія тіл відбувається вздовж певної лінії або через поверхню з певною площею або всередині деякого об'єму. Розподіленими називають таки сили, що діють вздовж лінії, розподілені за поверхнею, за об'ємом. Таки сили характеризуються інтенсивністю, яка являє собою векторну величину, модуль якої чисельно
дорівнює силі, що припадає на одиницю довжини ( ⃗g ), одиницю площі ( ⃗р ),
одиницю об'єму ( γ⃗ ).
За характером розподілу сили можуть бути рівномірно розподіленими та
нерівномірно розподіленими.
Розглянемо рівномірно розподілені сили за довжиною. Дію цих сил можна
замінити рівнодійною зосередженою силою Q⃗ , що чисельно дорівнює площі
фігури, яку називають епюрою: Q = g⋅l , де l – довжина лінії (рис. 1.3). Ця
рівнодійна сила Q⃗ прикладена до центра тяжіння епюри.
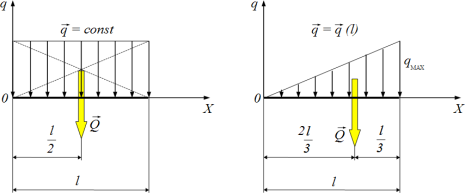
Рис. 1.3. Рівномірно та нерівномірно розподілені сили вздовж лінії
Нехай інтенсивність нерівномірно розподілених сил змінюється за
лінійним законом (рис. 1.3). Модуль рівнодійної розподілених сил Q⃗ чисельно
дорівнює площі епюри у вигляді трикутника ![]() , а точка її
, а точка її
прикладання збігається з центром тяжіння епюри, що знаходиться в точці перетину його медіан.
Інтенсивність сил, що розподілені за поверхнею, називають тиском. У найпростішому випадку рівномірного розподілу сил за поверхнею дію цих сил
можна замінити рівнодійною зосередженою силою
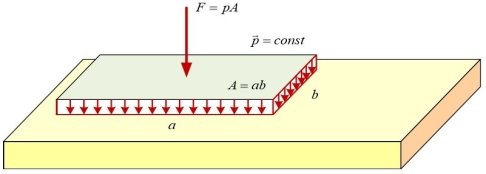
поверхні, на який діють розподілені сили. Точка сили збігається з центром тяжіння поверхні, де F⃗ = ⃗p ⋅A , де А — площа прикладання рівнодійної діють розподілені сили(рис. 1.4).
Рис.1.4 Сили, що розподілені за поверхнею
Аксіомами статики називають положення досвідного характеру, які приймаються без доведення. Вони встановлені багатьма безпосередніми спостереженнями, а також дослідною перевіркою наслідків, які логічно випливають з цих аксіом.
|
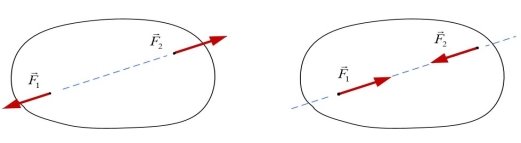
Аксіома 1: якщо на вільне тверде тіло діють дві сили, то це тіло перебуває в стані рівноваги тоді й лише тоді, коли ці сили однакові за модулем й напрямлені вздовж однієї прямої в протилежних напрямках |
|
|
|
Ця аксіома визначає найпростішу зрівноважену систему сил, оскільки досвід показує, що вільне тіло, на яке діє тільки одна сила, в рівновазі знаходитися не може.
|
|
Аксіома 2: дія даної системи сил на тверде тіло не зміниться, якщо до цієї системи сил приєднати або відкинути зрівноважену систему сил. |
|
|
|
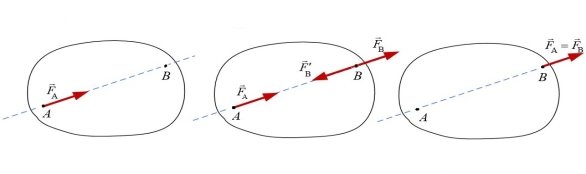
дія даної сили на тверде тіло не зміниться, якщо перенести точку прикладання цієї сили вздовж лінії її дії в будь-яку іншу точку тіла |
Для доведення наслідку розглянемо силу
F⃗A , що прикладена до тіла в
точці А. На лінії дії сили
F⃗A до довільної точки В прикладемо зрівноважену
систему сил (F⃗B,F⃗'B)~0, де ∣F⃗B∣=∣F⃗'B∣=∣F⃗A∣=F, ⃗F'B=−F⃗A. Згідно
аксіоми 1 сили
F⃗A і
F⃗ ' B утворюють зрівноважену систему сил
(F⃗А , F⃗ ' B) ~ 0, а згідно з аксіомою 2 цю зрівноважену систему сил можна
відкинути. Тоді на тіло діятиме тільки одна сила точки В.
F⃗В , яка прикладена до
Таким чином, дія сили на тіло не змінюється, оскільки F⃗B=F⃗A, але
змінюється її точка прикладання вздовж лінії дії сили F⃗A . Отже, наслідок
|
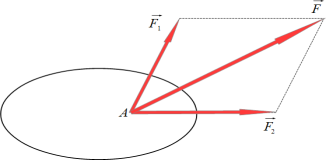
Аксіома 3: система з двох сил, що прикладені до тіла в одній точці під деяким кутом одна до одній, має рівнодійну, що прикладена до цієї самої точки тіла й за своїм модулем та напрямом визначається діагоналлю паралелограма, побудованого на цих силах, як на сторонах |
|
|
|
Паралелограм, побудований на даних силах називається паралелограмом сил, а сам спосіб знаходження рівнодійної шляхом побудови паралелограма називається правилом паралелограма.
|
доведено.
|
Аксіома 4: сили взаємодії двох твердих тіл завжди рівні за модулем й діють по одній прямій в протилежних напрямках |
|
|
|
Ця аксіома являє собою третій закон Ньютона, який показує на те, що коли одне тіло діє на друге з певною силою, то одночасно друге тіло діє на перше з такою самою силою. Слід зазначити, що сили взаємодії не утворюють зрівноваженої системи сил, тому що вони прикладені до різних тіл.
|
Розрізняють вільні та невільні тверді тіла. Тіло, переміщення якого в просторі ні чим не обмежено і яке може рухатися в будь-якому напрямку, називається вільним.
Тіло, переміщення якого в просторі в будь-якому напрямку обмежене деякими наперед заданими умовами, називається невільним. Тіло або сукупність тіл, які обмежують рух даного тіла, називають в'яззю. Отже, невільним тілом називають таке тіло, на яке накладені в'язі. Невільне тіло в просторі матиме можливість здійснювати стільки переміщень, скільки дозволено в'язнями.
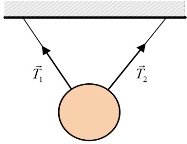
Сила, з якою в'язь діє на дане тіло, обмежуючи його рух, називається реакцією в'язі. Наприклад, нитка, на який підвішена куля, є в'яззю для цієї кулі, а сила натягу нитки є реакцією в'язі. Згідно аксіоми про сили взаємодії двох тіл сила, з якою дане тіло тисне на в'язь та реакція цієї в'язі завжди рівні за модулем й протилежні за напрямом та не утворюють зрівноваженої системи сил.
Поряд з розподілом сил на зовнішні та внутрішні їх поділяють на активні та пасивні. Особливістю активних сил є те, що їх модуль і напрям не залежать від інших сил, що діють на тіло. Прикладом активної сили є сила тяжіння. До пасивних сил відносять реакції в'язей, які залежать як від діючих на тіло інших сил, так й від характеру руху тіл та типу накладених на нього в'язей. Вони існують тільки тоді, коли тіло під дією активної сили тисне на в'язь. Якщо нема дії активної сили на в'язь, то й нема реакції в'язі.
Модуль та напрям реакції в'язі заздалегідь можна визначити лише тоді, коли в'язь перешкоджає рухові тіла тільки в одному напрямку. Якщо в'язі перешкоджають рухові тіла одночасно в кількох напрямках, то модуль й напрям реакцій в'язей заздалегідь визначити неможливо. Вони визначаються лише під час розв'язку відповідної задачі.
Розв'язок задач статики на рівновагу невільних тіл ґрунтується на аксіомі про звільнення від в'язей: будь-яке невільне тіло можна розглядати як вільне, якщо подумки звільнити його від в'язей та замінити їх дію на тіло реакціями цих в'язей.
Використовуючи цю аксіому, можна застосовувати до невільних тіл умови рівноваги вільних тіл. При цьому в рівняннях рівноваги до активних сил слід додати реакції відкинутих в'язей. Більшість задач статики зводяться до пошуку модулів та напрямів реакцій в'язей. Це дозволяє одержати дані, які необхідні для розрахунку міцності відповідних конструкцій.
Основні типи в'язей та покажемо напрям дії їх реакцій.
|
Ідеально гладенька поверхня |
|
така поверхня, коли між рухомим тілом й гладенькою поверхнею відсутні сили тертя |
|
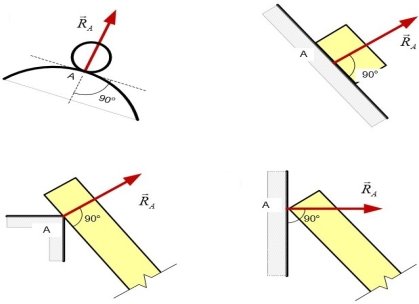
Оскільки гладенька поверхня не перешкоджає рухові тіла, то її реакція завжди напрямлена перпендикулярно до поверхонь взаємодіючих тіл у точці їх дотику. Коли одна з двох поверхонь, що дотикаються, має вістря, то реакція напрямлена вздовж нормалі до поверхні в'язі або тіла залежно від того, до якої з них можна провести нормаль |
|
|
|
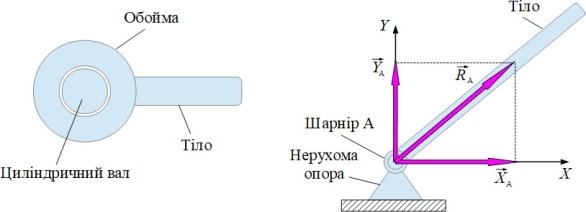
Шарнір – це з'єднання двох тіл, яке дає змогу одному тілу повертатися відносно іншого тіла. Шарніри поділяють на циліндричні й сферичні |
|
|
Циліндричний шарнір складається з обойми й циліндричного вала |
|
|
Тіло, яке жорстко скріплене з обоймою або валом шарніра, може тільки обертатися навколо осі шарніра. Напрям реакції циліндричного шарніра, виходячи тільки з конструкції шарніра, вказати неможливо. У більшості випадків реакцію шарніра можна подати у вигляді двох взаємно перпендикулярних складових |
|
|
|
|
|
Використовують – дверна завіса, ланцюг
|
|
|
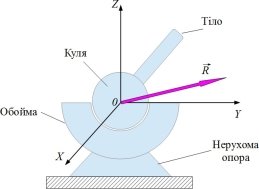
Сферичний шарнір дає можливість обертатися тілу навколо центра шарніра в будь-якому напрямку |
|
|
Напрям реакції шарніра також вказати неможливо Він залежить від характеру прикладених до тіла сил, але проходить центром шарніра. Якщо до тіла прикладена просторову систему сил, то реакцію шарніра виражають трьома взаємно перпендикулярними складовими |
|
|
|
|
|
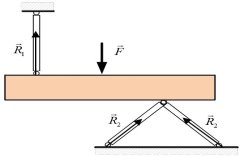
Ідеальний стержень – це невагомий тонкий стержень, який закріплений між двома шарнірами |
|
Реакція ідеального стержня напрямлена вздовж осі стержня протилежно до напряму дії активної сили |
|
|
|
Гнучка в'язь – це нитка, канат, ланцюг тощо |
|
Її реакція напрямлена вздовж в'язі протилежно до напряму дії активної сили |
|
|
- Павловський М.А. Теоретична механіка: підручник. Київ: Техніка, 2002. 511с.
- Бондаренко А.А., Дубінін О.О., Переяславцев О.М. Теоретична механіка. Ч. 1. Статика. Кінематика: підручник. Київ: Знання, 2004. 599 с.
- Путята Т.В., Фрадлін Б.Н. Методика розв’язування задач з теоретичної механіки: навч. посібник. Київ: Радянська школа, 1952. 365 с.
- ІвановБ.О., Максюта М.В. Конспект лекцій із теоретичної механіки: навч. посібник. Київ: Видав. центр “Київський університет”, 2012. 207с.
- Теоретична механіка. Ч. 1. Статика. Кінематика: навч. посібник / Литвинов О.І., Михайлович Я.М., Бойко А.В., Березовий М.Г. Київ: Агроосвіта, 2013. 576 с.
- Теоретична механіка: підручник / Булгаков В.М., Яременко В,В., Черниш О.М., Березовий М.Г. Київ: ЦУЛ, 2017. 640 с.


про публікацію авторської розробки
Додати розробку