Лекція з «Технічної механіки» Тема: «ЗГИН»

ВП НУБіП «Немішаївський агротехнічний коледж»

 

 

 

 

 

 

 

Лекція

 з «Технічної механіки»

 Тема: «ЗГИН»

 

Для студентів спеціальності

208 «Агроінженерія» ІІ курсу денної форми навчання

 

 

 

Викладач:  Лоїк О.А.

 

 

 

 

Немішаєве 2019

 

Згин

План заняття

1.Основні поняття та визначення. Класифікація видів згину.

2.Внутрішні силові фактори при прямому згині. Диференціальні залежності між згинаючим моментом, поперечною силою та інтенсивністю розподіленого навантаження.

3.Побудова епюр поперечних сил та згинаючих моментів.

4. Розрахунки на міцність при згині. Розрахунки на жорсткість при згині.

Згин - вид деформації, коли під дією зовнішніх сил в поперечному перерізі стержня (бруса) виникають згинальні моменти.

Якщо згинальний момент в перерізі є єдиним силовим фактором, а поперечні і нормальні сили відсутні, називається чистим. Якщо в поперечних перетинах стрижня поряд з згинаючими моментами діють і поперечні сили, вигин називається поперечним.

Іноді в поперечному стрижні виникає кілька силових факторів. Це складне опір. Розрахунки стержнів грунтуються на принципі незалежності дії сил.

Переміщення будь-якої точки осі балки, котра працює на згин, виражається вектором, початок якого суміщено з початковим положенням точки, а кінець — з положенням цієї самої точки у деформованій балці. У прямих балках переміщення точок які спрямовані перпендикулярно до початкового положення осі, називають прогинами і позначається  w(x). При згинанні відбувається також поворот перерізів стержня навколо осей, що лежать у площинах перерізів і позначається θ (x).

Умовна назва кривої лінії, що її форми набуває вісь балки (бруса) при згині у межах пружної деформації носить назву пружна лінія.

Стосовно до бруса розрізняють згин плоский, або простий, та складний. При плоскому (простому) згині зовнішні сили діють в одній з головних площин бруса (вони проходять через вісь бруса і головні осі інерції поперечного перерізу, див. Моменти інерції плоских перерізів), при складному згині — в різних площинах. Різновидом складного є косий згин, коли навантаження діють у площині, що не збігається з будь-якою з головних площин.

Залежно від сил, що діють у поперечному перерізі бруса, згин буває чистим (при наявності лише згинальних моментів), поперечним (діють поперечні сили), поздовжнім (випинання під впливом стискувальних сил, спрямованих вздовж осі) і поперечно-поздовжнім.

згин двотавра

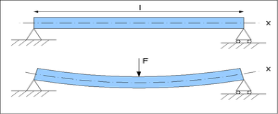
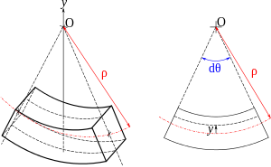
Схематичне зображення деформації згину навантаженої балки

 

 

Елемент балки, вирізаний двома суміжними поперечними перерізами, у здеформованому стані

Усі існуючі опори балок можна звести до наступних типів:

1. Шарнірно - рухома опора.

Характерна тим, що в ній виникає реакція, нормальна до опори.

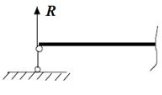Шарнірно-рухома опора

2. Шарнірно-нерухома опора .

Характерна тим, що на ній виникає реакція, яка може бути розкладена на дві складові: одна – нормальна до опори, а друга – вздовж балки.

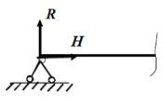Шарнірно-нерухома опора

3. Жорстке защемлення .

Характерне тим, що на ній, крім двох складових реакцій, може виникати ще й реактивний момент М_R.

 

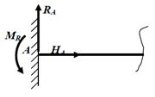Жорстке защемлення

4. Проміжні шарніри .

Проміжні шарніри – це елементи, які гасять і не передають згині моменти. Слід зауважити, що сума моментів відносно центра шарніра від сил, взятих із одного боку від шарніра, дорівнює 0.

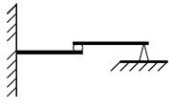Проміжні шарніри

Внутрішні силові фактори при згині.

Розглядаючи згин, введемо на додаток до основних гіпотез опору матеріалів ще деякі гіпотези, характерні для згину:

- будемо розглядати перерізи, що мають хоча б одну вісь симетрії, причому навантаження будемо проводити саме в площині симетрії;

- перерізи, нормальні до осі балки, залишаються плоскими в процесі деформації (гіпотеза плоских перерізів);

- сусідні волокна балки (уявимо її волокнистою структурою) не тиснуть одне на одне.

Розглянемо довільно навантажену в напрямі, нормальному до осі, балку . Користуючись методом перерізів, розріжемо цю балку в довільному перерізі – „І-І” на відстані x від лівої опори та відкинемо праву, наприклад, частину .

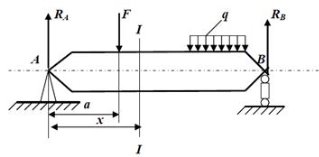Довільно навантажена балка

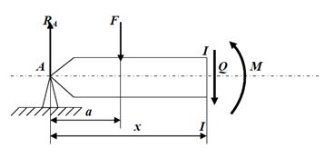Внутрішні силові фактори при згині

 

Частина, що залишається, повинна знаходитися в рівновазі. Тоді сума сил і моментів, що діють відносно перерізу „І-І”, повинні дорівнювати 0. Це можливо тільки у випадку, коли замість дії відрізаної частини у перерізі прикласти зосереджену силу Q та момент M , які будуть дорівнювати алгебраїчній сумі всіх сил і моментів відповідно, взятих зліва від перерізу. Тобто, з точки зору рівноваги можна записати

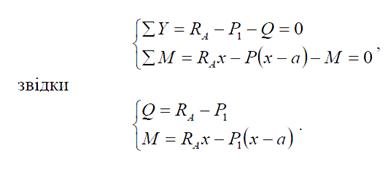
У даному випадку розглядаємо вже 2 внутрішніх силових фактори – перерізаючу силу Q (яку ще називають «поперечною силою») та згинаючий момент M.

Згідно з методом перерізів, перерізаючу силу Q та згинаючий момент М підраховують як алгебраїчні суми відповідних величин, взятих із одного боку від перерізу.

Встановимо правила вибору знаків. Якщо підрахунок сил проводиться зліва, то сила направлена догори – додатна. Якщо справа – навпаки, достатньою буде сила, направлена вниз. Для моментів правило знаків вибирають так: якщо момент вигинає балку опуклістю вниз – він додатний, якщо навпаки – від’ємний.

За рахунок наявності в перерізі, нормальному до осі балки, зразу двох силових факторів Q та M , у ньому в загальному випадку виникають як нормальні, так і дотичні напруження.

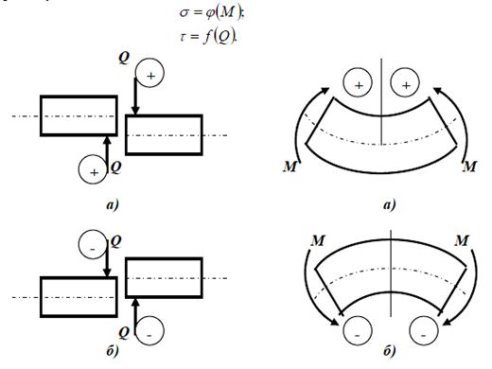
Очевидно, чим більшими у перерізі будуть Q та М, тим більшими будуть і відповідні напруження (за умов, що балка має один і той же переріз по всій довжині). Тому визначення небезпечного перерізу (тобто перерізу, в якому виникають найбільші напруження) пов’язано з визначенням функцій розподілу перерізаючої сили Q та згинаючого моменту M . Це можна робити як аналітичним шляхом, так і шляхом побудови епюр розподілу цих величин. На практиці застосовують обидва шляхи. Користуючись аналітичними залежностями, проводять розрахунки, а епюри використовують для якісного оцінювання факторів згину (характер розподілу величин, орієнтація розтягнутих волокон тощо).

Між згинаючим моментом, поперечною силою і інтенсивністю розподі­леного навантаження існують диференціальні залежності, в основі яких лежить теорема Журавського, названа так за ім'ям визначного російсько­го інженера-мостобудівника Д. І. Журавського (1821-1891). Цю тео­рему формулюють так: поперечна сила дорівнює першій похідній від згинаючого моменту по абсцисі пе­рерізу балки

 

Якщо рівняння згинаючих моментів (для ділянок з рівномірно розподіленим навантаженням) про диференціювати вдруге, то матимемо

 

Друга похідна від згинаючого моменту або перша похідна від поперечної сили за абсцисою перерізу балки дорівнює інтенсивності розподіленого навантаження.

При побудові епюр поперечних сил і згинаючих моментів рекомендується дотримуватись такої послідовності:

1) Визначити реакції опор (для консолі їх можна не знаходити).

2) Розбити брус на ділянки, границями яких є перетини в яких прикладені зосереджені сили і пари або розпочинається чи закінчується розподільне навантаження. Такі перетини називаються характерними.

3) Користуючись методом перетинів, будуємо епюру поперечних сил. Якщо поперечна сила, змінюючись неприривно, проходить через нульове значення, то необхідно визначити абсцису перерізу, де Q стає нульовим.

4) Визначити в характерних перетинах значення згинаючих моментів і по знайденим ординатам побудувати епюру М_х.

 Взаємозв’язок між видами епюр і навантаженням.

Для епюри поперечних сил.

1) На ділянках, де прикладено рівномірно розподільне навантаження, епюра - похила пряма, нахил прямої до осі балки залежить від інтенсивності навантаження.

2) На ділянках, вільних від  рівномірно розподільного навантаження, епюра – пряма паралельна осі балки.

3) В перетинах  де прикладено зосереджену силу, значення поперечної сили змінюється стрибкоподібно, причому стрибок дорівнює модулю цієї сили.

4) В перетинах де прикладено пару сил, значення поперечної сили не змінюється.

5) В кінцевих перетинах балки поперечна сила чисельно дорівнює зосередженим силам, які прикладені у цьому перерізі. Якщо в кінцевому перерізі не прикладені зосереджені сили, поперечна сила в них рівна нулю.

Для епюри згинаючих моментів.

  1) На ділянках, де прикладено рівномірно розподільне навантаження, епюра моментів є параболою. Опуклість параболи направлена в сторону протилежну дії навантаження (на зустріч навантаженню).

2) На ділянках, вільних від  рівномірно розподільного навантаження, епюра моментів похила пряма. Під зосередженими силами на епюрі получаються згини, тобто для декількох ділянок епюра - ломана лінія.

3) В перерізі де прикладено пару сил, значення згинаючого моменту змінюється стрибкоподібно, причому стрибок дорівнює моменту пари.

4) На кінці балки згинаючий момент дорівнює нулю, якщо там не прикладено пару сил. Якщо в кінцевому перерізі прикладено зовнішню пару сил то згинаючий момент дорівнює моменту пари.

5) На ділянках де Q = 0, балка відчуває чистий згин і епюра згинаючих моментів – пряма паралельна осі балки.

6) Згинаючий момент має екстремальне значення (max або min) в перетинах де змінюється знак поперечної сили.

При поперечному згинанні балки її матеріал перебуває в плоскому напруженому стані. При цьому умова міцності може бути записана для трьох небезпечних точок поперечного перерізу балки:

а) точка, де нормальне напруження досягає найбільшого значення;

б) точка, де дотичне напруження досягає найбільшого значення;

в) точка, де σ і τ хоч і не набувають найбільших значень, але в своїй сукупності створюють найвигіднішу комбінацію, тобто найбільше еквівалентне напруження за прийнятою для розрахунку теорією міцності.

Якщо орієнтуватися на першу небезпечну точку, умову міцності можна записати у вигляді

Друга небезпечна точка лежить на нейтральній лінії, умова міцності виглядає так:

 

В третій небезпечній точці завжди буде плоский напружений стан. Тому застосовуючи третю теорію міцності, будемо мати таку формулу для еквівалентних напружень:

Ця теорія рекомендується для розрахунку балок з пластичних матеріалів.

На практиці здебільш небезпечною є крайня точка поперечного перерізу балки, де М = М_max,, тому перевірний розрахунок балок виконується в такій послідовності:

-знаходять небезпечний переріз балки, тобто той переріз, в якому діє найбільший за абсолютним значенням згинальний момент;

-за таблицею чи розрахунками визначають момент опору W поперечного перерізу відносно нейтральної лінії;

-визначають максимальні напруження та зрівнюють їх з допустимими, застосовуючи тільки одну умову міцності по формулі, яку називають основною.

За цією схемою для більшості профілів можна легко виконати також проектувальний розрахунок. Тоді умова міцності записується у вигляді: 

Визначивши потрібний момент опору балки та вибравши певний профіль поперечного перерізу, добирають його розміри.

Література:{\displaystyle Q_{y}={\frac {GF}{\alpha }}\left(\theta (x)-{\frac {\,dw(x)}{\,dx}}\right)}

1.Опір матеріалів. Підручник /Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. — К.: В. школа,1993. 

2.Опір матеріалів: Навч. посіб. для студентів ВНЗ. Рекомендовано МОН / Шваб'юк В. І. — К., 2009. 

3.Опір матеріалів. Конспект лекцій /Олександр Володимирович Мильніков. — Т.: Видавництво ТНТУ, 2010.