Лекційні матеріали до теми "Практичні розрахунки на зріз та зминання"

Лекція з дисципліни «Технічна механіка»

Галузь знань: 20 «Аграрні науки та продовольство»

Розробила викладач Лоїк О.А.

Практичні розрахунки на зріз і зминання

1. Чистий зсув.
2. Закон Гука для зсуву. Модуль зсуву. Залежність між трьома пружними постійними для ізотропного тіла (без виведення).
3. Зріз. Основні припущення та розрахункові формули.
4. Зминання, умовності розрахунку, розрахункові формули.

Деформа́ція зсу́ву — вид деформації, при якому величина зміщення кожної точки тіла зростає в напрямку, перпендикулярному до напрямку зміщення.

Деформація зсуву виникає, якщо закріпити тіло в основі й прикласти силу (F) до бічної грані.

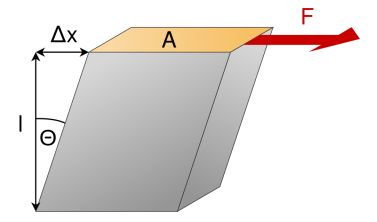
Відносна деформація зсуву визначається за формулою:

{\displaystyle \mathrm {tg} \,\theta ={\frac {\triangle X}{l}}},

де ΔX — абсолютний зсув паралельних шарів тіла один відносно одного; l — відстань між шарами.

У практичних випадках деформація зсуву у чистому вигляді (чистий зсув) трапляється нечасто. Частіше виникає деформація згину, яка є комбінацією зсуву із розтягом та стисканням або деформація кручення, котра є особливим випадком деформації зсуву. Проте при математичному описі деформації загального вигляду деформація зсуву є базовою.

Деформація зсуву може бути отримана у першому наближенні, коли на стрижень діють дві рівні по величині і протилежно спрямовані сили, перпендикулярні до осі стержня. Прикладом такої дії сил на брус може бути різання ножицями металевих прутків.

При розрахунках на зсув умовно приймається рівномірний закон розподілу дотичних напружень τ по перерізу, тобто τ = const. Тоді:

{\displaystyle \tau ={\frac {F}{A}},}

тут A — площа зрізу.

Як і при будь-якому розрахунку опору матеріалів напруження в матеріалі повинні зіставлятися з напруженням, що допускається (допустиме напруження), тобто умова міцності на зріз має вигляд:

{\displaystyle \tau ={\frac {F}{A}}\leq [\tau ],}{\displaystyle \tau ={\frac {F}{A}},}

Допустиме напруження при зсуві приймається рівним: {\displaystyle [\tau ]\approx 0,5...0,6[\sigma ]}.

Дослідне вивчення зсуву в матеріалах проводиться на спеціальних тонкостінних трубках, що навантажуються крутним моментом до руйнування. У результаті цього одержують діаграму зсуву, що для пластичного матеріалу має вигляд подібний до діаграми деформування при розтягу. По діаграмі можна визначити характеристики міцності матеріалу при зсуві (зрізі).

Границя пропорційності {\displaystyle \tau }τ_пц матеріалу при зсуві — це найбільше напруження, до якого виконується закон Гука.

Границя текучості τ{\displaystyle \tau }_т — це найменше напруження, при якому відносний зсув зростає при практично постійному навантаженні.

Границя міцності τ{\displaystyle \tau }_в при зсуві — це максимальне напруження в матеріалі, при якому не настає руйнування

Закон Гука для зсуву

Як показують експерименти у певному діапазоні деформацій, існує лінійна залежність між дотичним напруженням {\displaystyle \tau }τ, відносним зсувом {\displaystyle \gamma }γ та модулем зсуву G, тобто закон Гука при зсуві:

{\displaystyle \tau =G\cdot \gamma }

Зв'язок трьох пружних сталих для ізотропного матеріалу (модуля Юнга E, модуля зсуву G і коефіцієнта Пуассона ν) визначається залежністю:

{\displaystyle G={\frac {E}{2(1+\nu )}}}

Отже, модуль Юнга, модуль зсуву і коефіцієнт Пуассона є характеристиками пружних властивостей матеріалу.

Деталі, які служать для з’єднання окремих елементів машин чи будівельних конструкцій (штифти, заклепки, болти, шпонки тощо), у багатьох випадках сприймають навантаження, перпендикулярні до їх поздовжньої осі. Руйнування з’єднуючих деталей (у випадку недостатньої міцності) відбувається в результаті їх перерізання по площині, яка співпадає з поверхнею дотикання з’єднуваних деталей.

На практиці багато деталей конструкцій зазнають деформацій, близьких до деформації зсуву, і в таких випадках їх розміри визначають з розрахунку на зсув (зріз). Розглянемо, наприклад, роботу заклепки, що скріплює два стальних листи.

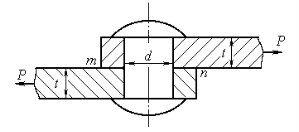
Нехай на листи діють сили P, що намагаються зсунути їх один відносно одного. Цьому зміщенню перешкоджатиме стержень заклепки. На стержень заклепки передаються зусилля Р, які намагаються зрізати заклепку по площині mn.

Дотичні напруження розподіляються по перерізу заклепки рівномірно (згином заклепки нехтуємо). Тоді їх величина

де  площа поперечного перерізу заклепки.

Заклепкові з'єднання відносяться до нероз'ємних з'єднань, так як для їх розбирання необхідно зруйнувати сполучні елементи - заклепки.

Умова міцності при розрахунку заклепок на зріз враховує їх кількість для з’єднання, тому вона має вигляд:

n – кількість заклепок, штифтів, болтів (гвинтів) або шпонок, що знаходяться в площині зрізу.

Позначимо через [] допустиме напруження матеріалу заклепки на зріз. Тоді умова міцності матиме вигляд

У машинобудуванні під час розрахунків штифтів, болтів, шпонок тощо приймають

,

де  , – границя текучості та допустима напруга розтягу відповідно для матеріалу деталі.

Зминанням називається місцева деформація стиснення по майданчиках передачі тиску. Для простоти розрахунків вважають, що при контакті по площині виникають нормальні напруження зминання, рівномірно розподілені по площі контакту. Розрахункове рівняння на зминання має вигляд:

де F – стискаюча сила, Н;

А_зм – площа контакту деталей, мм² ;

_зм– допустимі напруження на зминання, МПа.

Якщо деталі, що контактують виготовлені з різних матеріалів, то на зминання перевіряють деталь з більш м'якого матеріалу, тобто матеріал, що має меншу допустиме напруження. При контакті двох деталей по циліндричній поверхні (наприклад, заклепкове або різьбове з'єднання) закон розподілу напружень зминання по поверхні контакту досить складний .

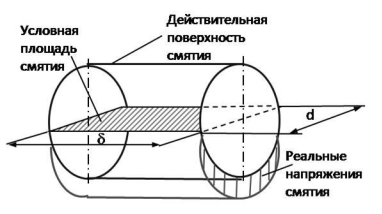
Тому при розрахунку на зминання циліндричних отворів, в розрахункову формулу підставляють не площу бічної поверхні циліндра, а площу діаметрального перетину отвору (умовна площа зминання):

де δ – товщина деталі, що з'єднується (висота циліндра), мм

 d – діаметр отвору, мм.

При різній товщині деталей, що з'єднуються в формулу підставляють меншу товщину.

У машинобудуванні до­пустимі напруги на зми­нання для болтових, штиф­тових і шпонкових з'єднань з маловуглецевої сталі бе­руть у межах МПа,

для заклепоч­них з'єднань МПа,

для деревини (сосна, дуб)  МПа залежно від сорту деревини і напрямку стискальної сили відносно напрямку волокон.

Крім напружень зрізу виникають і напруження зминання з урахуванням кількості деталей, що знаходяться в з'єднанні і особливостей визначення площі зминання для кожного з'єднання. Даний рисунок  ілюструє наявність поверхні зрізу і зминання для деталей кріплення на прикладі болтового з’єднання.

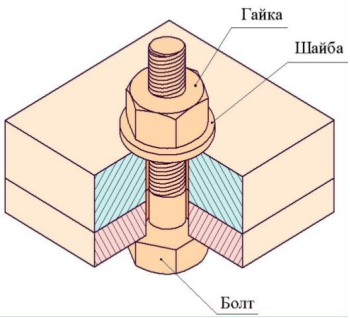
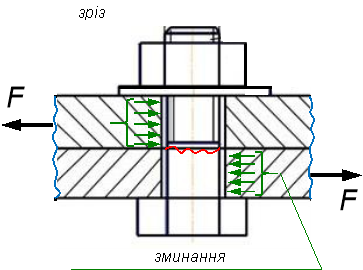
Рисунок– Болтове з’єднання (а) та деформації, що в ньому виникають (б).

Шпонкові з’єднання також розраховують на зріз та зминання. Враховуючи те, що колові зусилля діють на шпонку у різних напрямках, приймаємо їх дію на половині висоти (t₁ = h/2) у кожному напрямку.

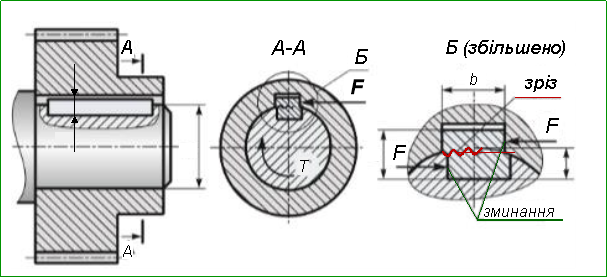
Для шпонок площу зрізу ,

де ширина шпонки, мм,

ℓ – довжина шпонки, мм.

Площа зминання

де 0,5·h – глибина врізання шпонки у вал, мм,

ℓ_р – розрахункова довжина шпонки, величина якої залежить від виду шпонки, мм.

Практичні розрахунки на зріз і зминання носять умовний характер і базуються на наступних припущеннях:

• Передбачається, що в поперечних перерізах стержня виникає тільки один внутрішній силовий фактор - поперечна сила Q;
• Передбачається, що дотичні напруження, що виникають в поперечному перерізі, розподілені по його площі рівномірно.
• Передбачається, що якщо з'єднання здійснено декількома однаковими деталями (заклепками), то всі вони навантажені однаково.

Література:

1. Опір матеріалів. Підручник /Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993 . 
2. Мильніков О. В. Опір матеріалів. Конспект лекцій. − Тернопіль: Видавництво ТНТУ, 2010.
3. Цурпал І.А. Механіка матеріалів і конструкцій: навч. посібник / І.А. Цурпал – К.: Аграрна освіта, 2005.