Лінійне рівняння з однією змінною

Тема. Лінійне рівняння з однією змінною

Мета: систематизувати знання учнів про види й. способи розв'язання рівнянь з однією змінною, що зводяться до лінійних; відпрацювати навич­ки застосовувати ці знання на практиці.

Тип уроку: засвоєння навичок, діагностика засвоєння.

Хід уроку

І. Перевірка домашнього завдання

 Оскільки № 1 (1, 2, 3, 5, 6) домашнього завдання є вправою на закріплення вмінь, набутих на попередньому уроці, достатньо пере­вірити відповіді до вправ (у слабких учнів вибірково беремо зошити на перевірку).

Розв'язання і відповіді до № 1 (1, 2, 3, 5, 6) домашнього завдання

1) |2x – 3| = 5; 2х – 3 = 5 або 2x – 3 = -5. Відповідь. 4; -1.

2) |2х – 1| + 7 = 8; |2x – 1| = 1; 2x – 1 = 1 або 2x – 1 = -1. Відповідь. 1; 0.

3) |5x – 4(2х + 3)| = 6; |-3х – 12| = 6; |3x + 12| = 6; 3x + 12 = 6 або 3x + 12 = -6. Відповідь. -2; -6.

5) 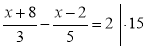; 5(х + 8) – 3(х – 2) = 30; 2x + 46 = 30; 2х = -16; x = -8. Відповідь. -8.

6) 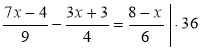; 4(7х – 4) – 9(3х + 3) = 6(8 – х);

28х – 16 – 27х – 27 = 48 – 6х; х – 43 = 48 – 6х; 7х = 91; х = 13. Відповідь. 13.

II. Робота з випереджальним домашнім завданням

1. На дошці записано умову рівняння № 4 і 1 – 3.

Пропонуємо учням виконати роботу з порівняння цих рівнянь (див. алгоритм).

Після виконання роботи робимо висновки щодо способу розв'язання:

1. Оскільки рівняння містить змінну під знаком модуля, його треба зве­сти до вигляду |х| = а.
2. Щоб виконати п. 1), необхідно здійснити рівносильні перетворення
   відносно |х|.

Тільки тоді можна зробити відповідні записи:

2(|х| - 3) – 4(2|х| + 9) = -48;

2|х| - 6 – 8|х| - 36 = -48;

-6|х| - 42 = -48;

-6|х| = -6;

|х| = 1;

х = 1 або х = -1.

Відповідь. 1; -1.

2. На дошці записано рівняння ах = 42.

Перш ніж перевіряти відповіді, проведемо бесіду.

• Яке число будемо називати коренем рівняння?
• Якого виду рівняння?
• Які випадки розв'язування лінійного рівняння ах = b з однією змінною (залежно від значень а і b) ви знаєте?
• Який з випадків (див. вище) неможливий?

По закінченні бесіди:

1. корінь х = 7, отже, а · (+7) = 42, а = 42 : 7, а = 6;
2. коренів немає, отже, а = 0;
3. цей випадок неможливий (такого а для даного рівняння не існує).

III. Систематизація знань

Бесіда

1. Що називається коренем рівняння з однією змінною?
2. Що означає розв'язати рівняння?
3. Які два рівняння називаються рівносильними?
4. Які властивості рівносильних рівнянь ви знаєте?
5. Яке рівняння називається лінійним рівнянням з однією змінною?
6. В якому випадку рівняння ах = b має один корінь; не має коренів? В якому випадку будь-яке число є коренем цього рівняння?
7. Наведіть приклад лінійного рівняння, що:

а) має один корінь; б) не має коренів.

8. Установіть логічний зв'язок між поняттями 1 – 7.

Висновки. Більшість рівнянь з однією змінною, які ми розв'язували останнім часом шляхом рівносильних перетворень, зводили до лінійних рівнянь з однією змінною, які потім розв'язували відповідно до схеми (див. конспект 2).

IV. Засвоєння навичок

 Оскільки на цей момент базові вміння щодо класифікації і розв'я­зання рівнянь з однією змінною, що зводяться до лінійних рівнянь виду ах = b, повинні бути сформовані, для розв'язання на уроці про­понуємо учням завдання достатнього та високого рівня.

1. Розв'яжіть рівняння:

1) 1,8(1 – 2х) = -2(1,8х + 3) + 7,8;

2) 0,5(8х – 3) = -0,4(2,5 – 2х);

3) |3х – 2| + 5 = 7;

4) 3 – 2(1 – 2|х|) = 11 – |х|;

5) .

2. Дано рівняння (а – 2)х = 6. Знайдіть значення а, при якому:
   1) рівняння не має коренів;

2) рівняння має корінь 1;

3) коренем є число, що є і коренем рівняння 4х – 7 = 5.

V. Діагностика засвоєння вмінь Самостійна робота

VI. Рефлексія

Способи дій під час розв'язування рівнянь були опрацьовані в попе­редній частині уроку, тому після виконання самостійної роботи достатньо лише звірити відповіді.

Розв'язання та відповіді до завдань самостійної роботи

Варіант 1

1) 6х – 12 = 4х – 8; 2х = 4; х = 2. Відповідь. 2.

2) 4(х – 0,5) – 2(х + 0,3) = -2,6; 4х – 2 – 2х – 0,6 = -2,6; 2х = 0; х = 0. Відповідь. 0.

3) ; 3(х – 1) – 2(х + 1) = 6; 3х – 3 – 2х – 2 = 6; х = 11.  Відповідь. 11.

4) 3|2х + 1| - 7 = 2; 3|2х + 1| = 9; |2х + 1| = 3; 2х + 1 = 3 або 2х + 1 = -3;

х = 1 або х = -2. Відповідь. 1; -2.

Варіант 2

1) 5у – 8 = 2y – 5; 3у = 3; у = 1. Відповідь. 1.

2) 0,2(3х – 5) – 0,3(х – 1) = -0,7; 0,6х – 1 – 0,3х + 0,3 = -0,7; 0,3х = 0; х = 0. Відповідь. 0.

3) ; 2·3х – 5(х + 1) = 10; 6х – 5х – 5 = 10; х = 15. Відповідь. 15.

4) 2|3х – 1| - 5 = 3; 2|3х – 1| = 8; |3х – 1| = 4; 3х – 1= 4 або 3х – 1 = -4;

х = 1 або х = -1. Відповідь. 1або -1.

VII. Домашнє завдання

№ 1. Творче завдання^[*]. Скласти три рівняння, що зводяться до ліній­них (з модулем, з дробами і таке, що зводиться до лінійного шляхом рів­носильних перетворень і не має коренів).

№ 2. Випереджальне завдання (учні отримують ксерокопії завдання або працюють із відповідним текстом підручника).

Розгляньте умову і розв'язання задачі.

У двох цистернах зберігається 66 т бензину, причому в першій бензину в 1,2 раза більше, ніж у другій. Скільки бензину в кожній цистерні?

Розв'язання. Нехай у другій цистерні х т бензину, тоді в першій — 1,2х т. У двох цистернах разом є (х + 1,2х) т бензину, що за умовою дорівнює 66 т. Маємо рівняння: х + 1,2х = 66; 2,2х = 66; х = 66 : 2,2; х = 30.

Отже, у другій цистерні було 30 т бензину, а в першій — 1,2 · 30 = 36 (т).

Відповідь. 36 т; 30 т.

Розбийте розв'язання на змістові частини (виділіть у тексті кожну ок­рему частину різними кольорами).

Складіть за поданим розв'язанням план. Чи можна було розв'язати цю задачу іншим способом? Яке розв'язання краще?

^[*] Замість творчого завдання можна запропонувати домашню самостійну роботу на розв'язування рівнянь, що зводяться до лінійних та на перевірку матеріалу, вивченого в темі «Рівняння з однією змінною».