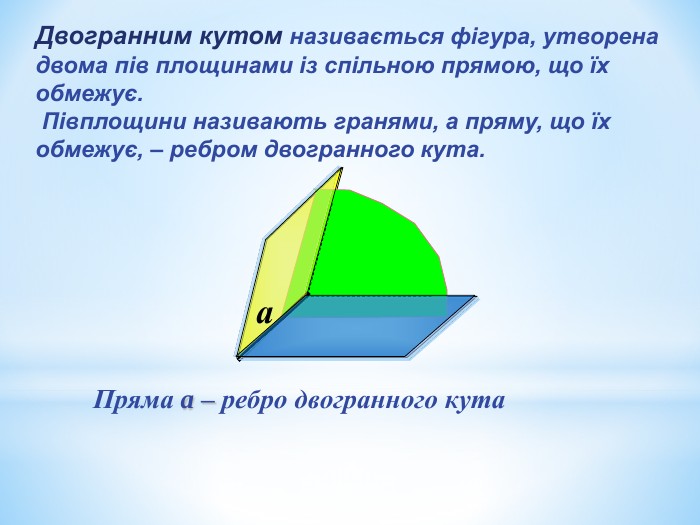
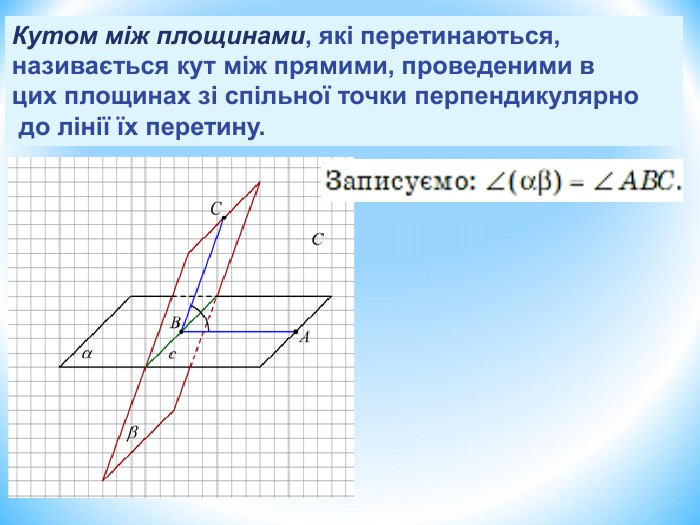
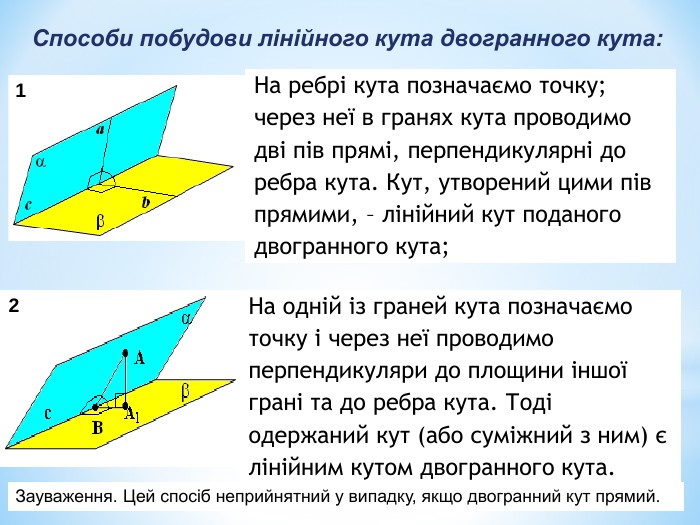
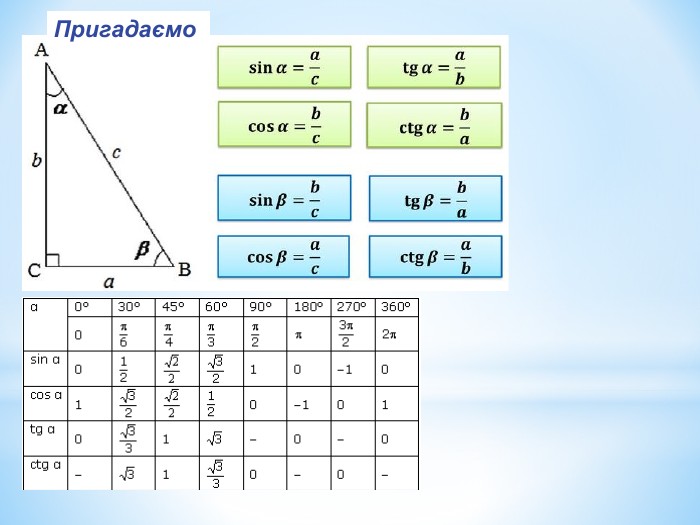
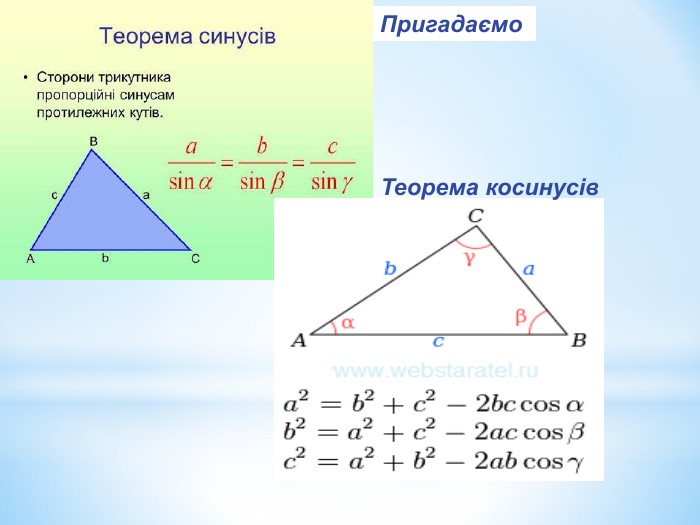
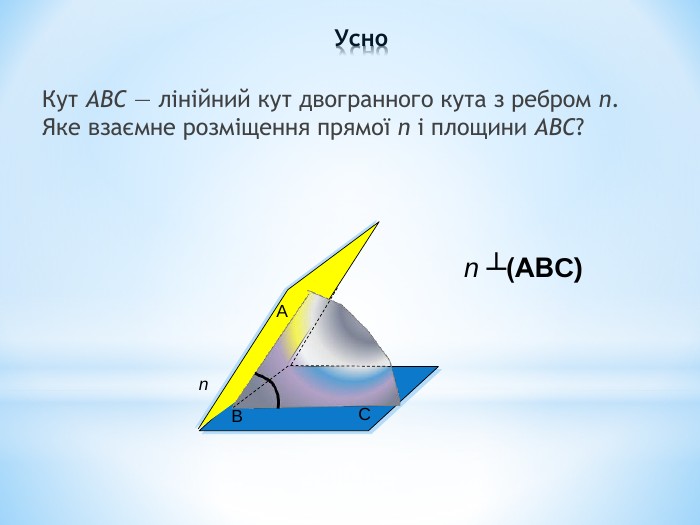
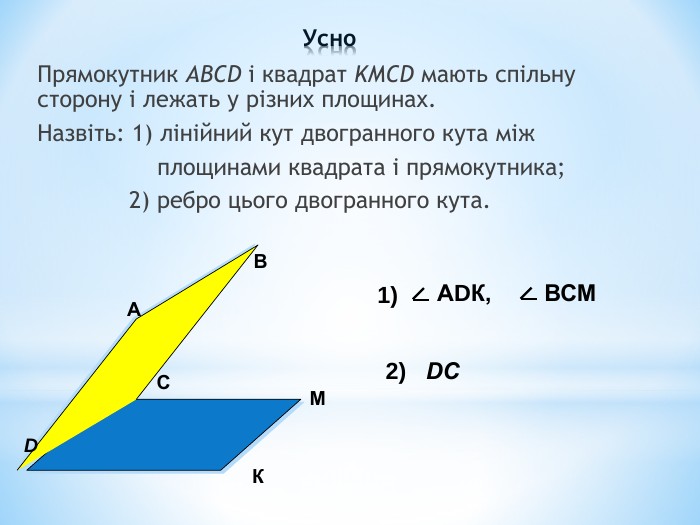
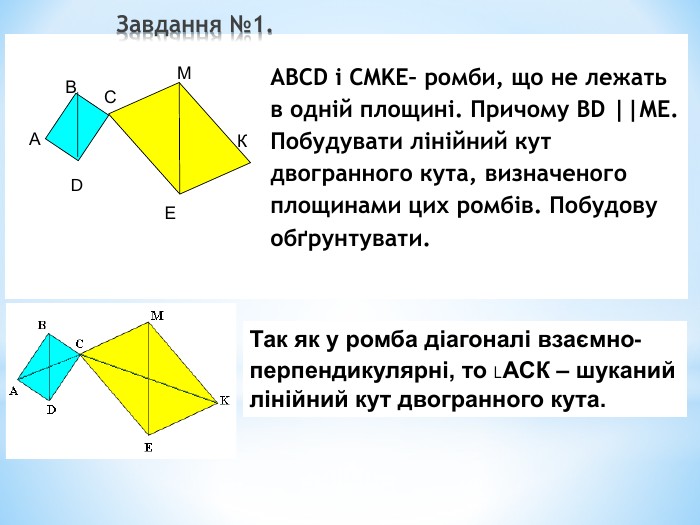
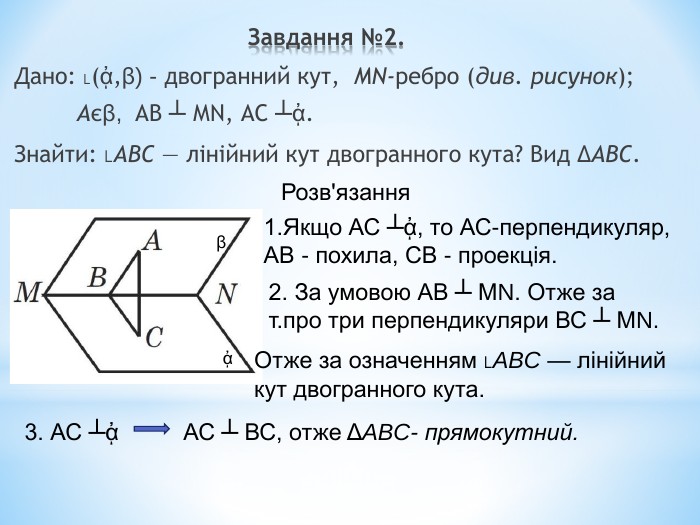
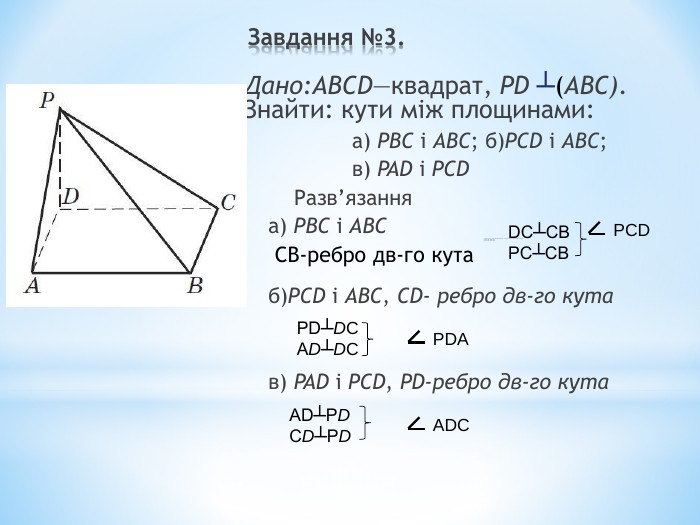
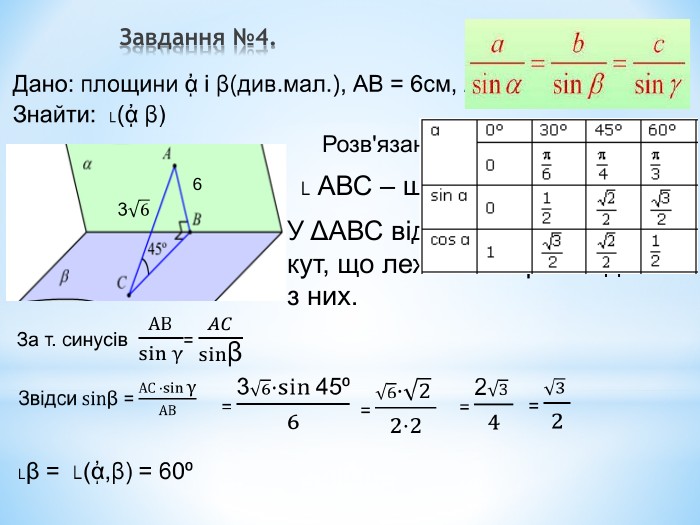
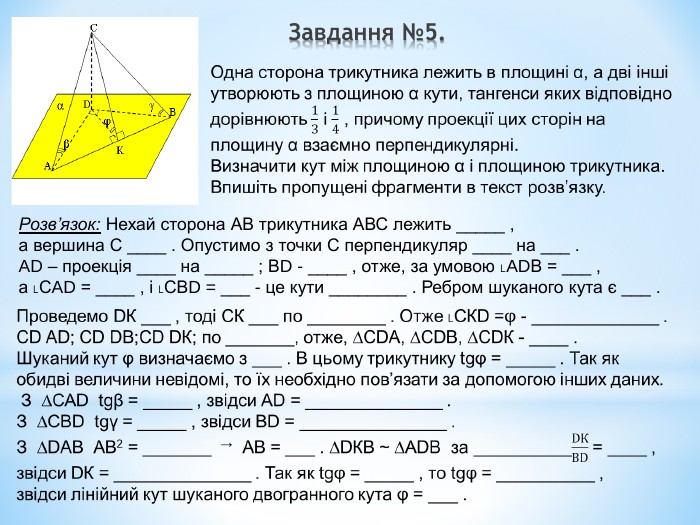
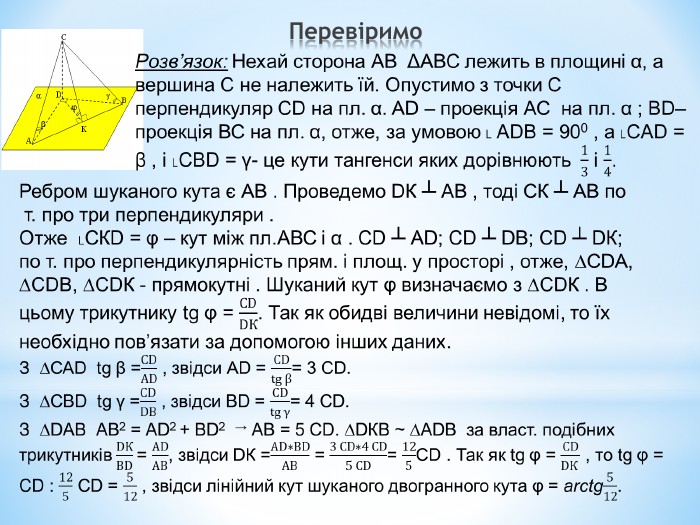
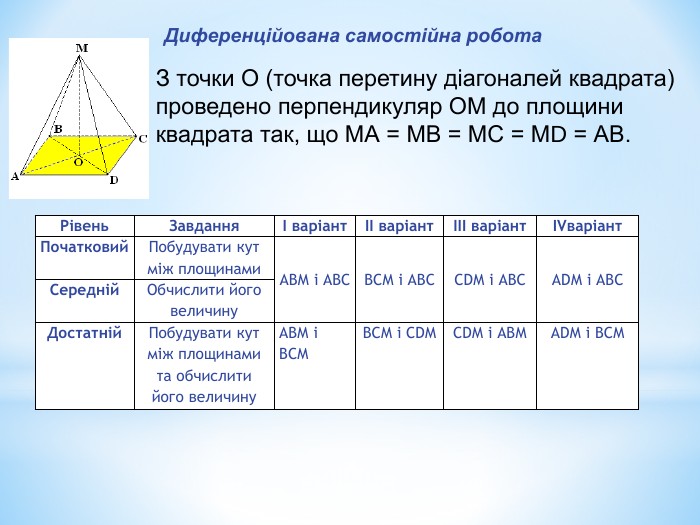
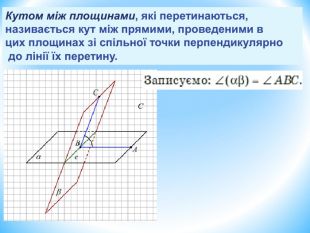
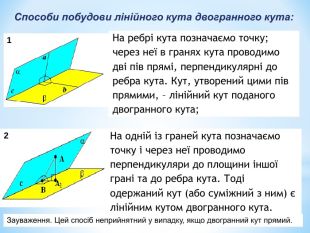
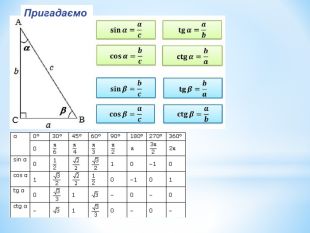
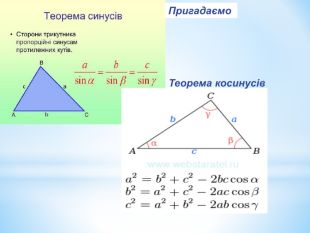
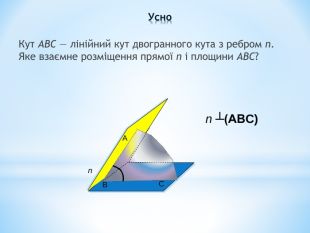
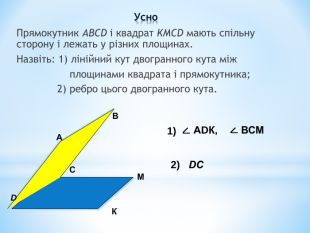
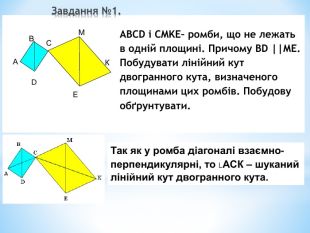
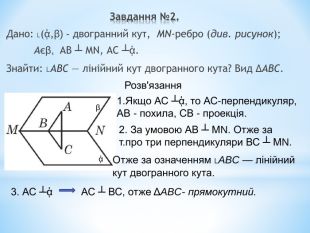
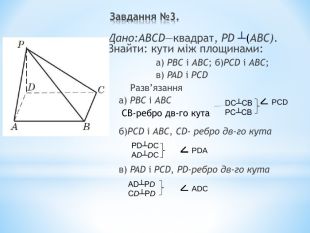
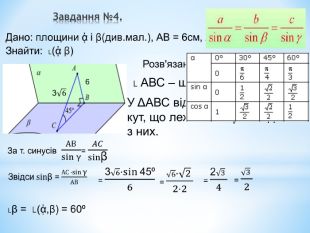
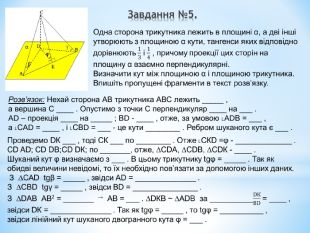
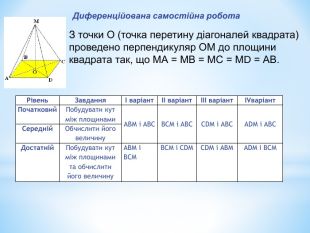
Лінійний кут двогранного кута. Кут між площинами.
Про матеріал
Дана презентація створена для проведення спарених уроків геометрії за темою "Лінійний кут двогранного кута. Кут між площинами." під час дистанційного навчання. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку