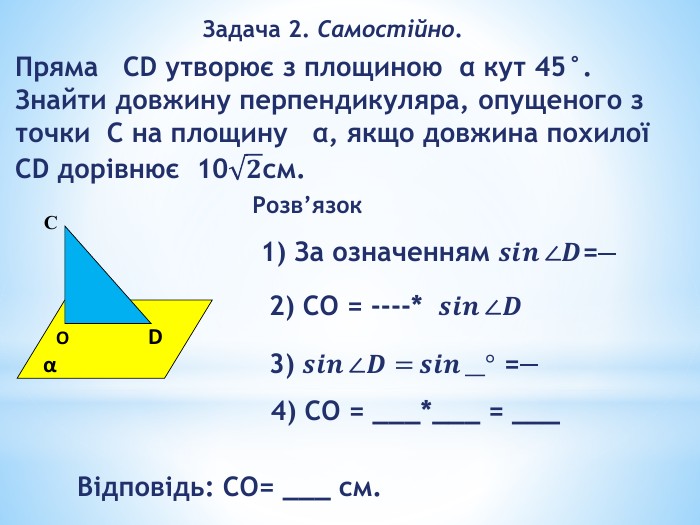
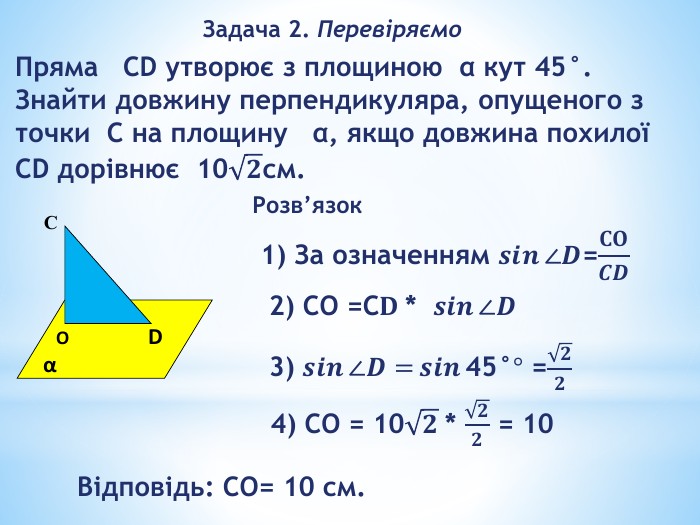
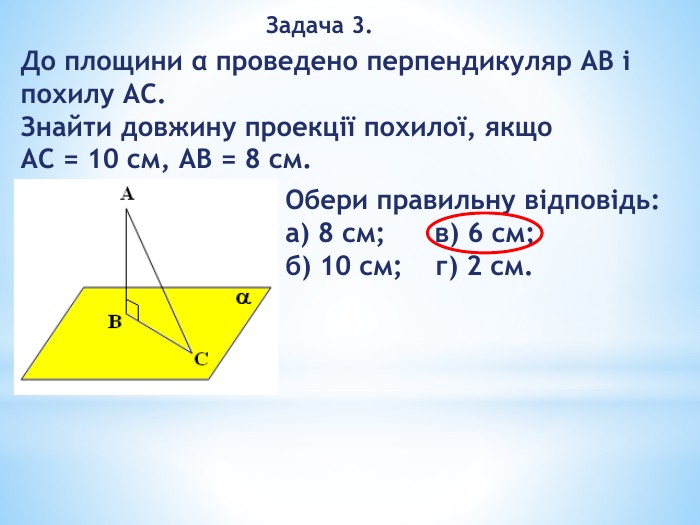
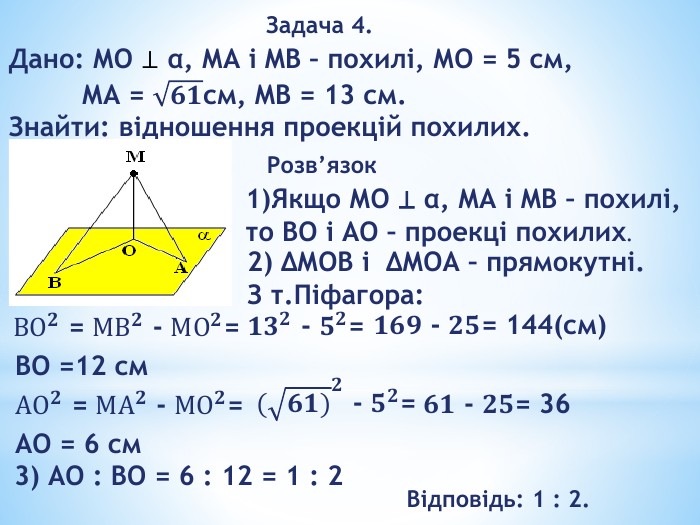
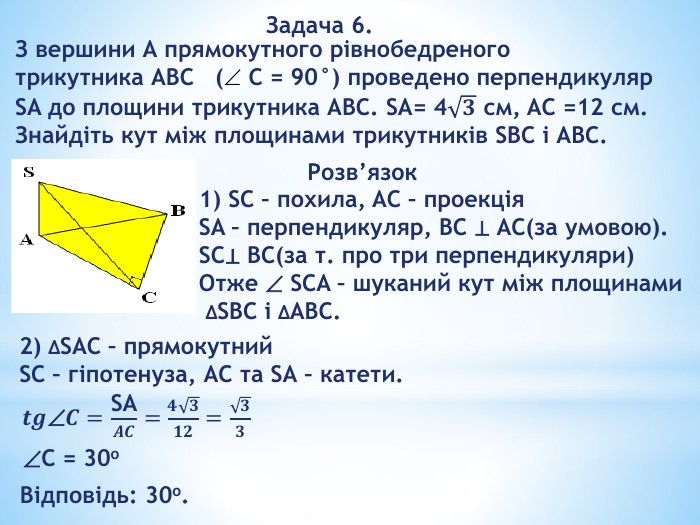
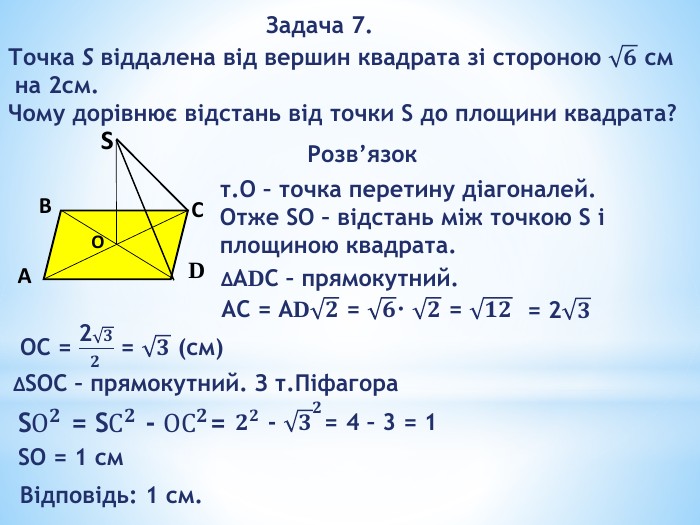
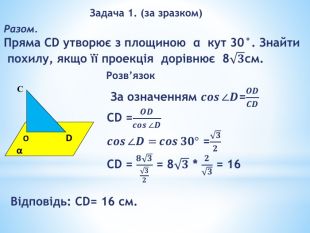
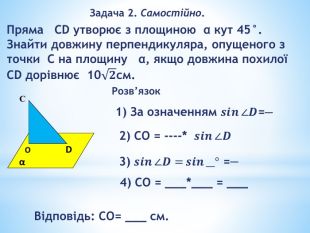
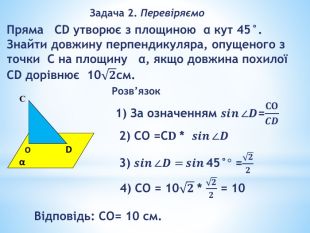
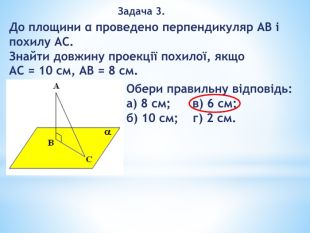
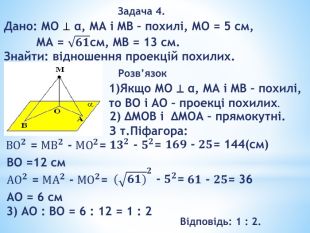
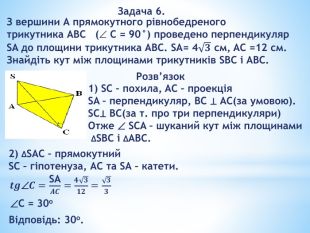
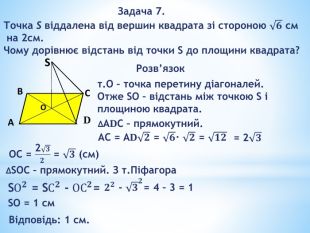
«Перпендикулярність прямих і площин у просторі»
Про матеріал
Дана презентація створена до уроку систематизації і узагальнення знань з теми «Перпендикулярність прямих і площин у просторі». Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку