МЕТОДИКА ВИВЧЕННЯ КООРДИНАТ І ВЕКТОРІВ У ПРОСТОРІ

1.                 Означення вектора. 

2.                 Координати вектора, його абсолютна величина. 

3.                 Рівність векторів. 

4.                 Правило трикутника для додавання векторів. 

5.                 Сума векторів через координати. 

6.                 Задачі на знаходження координат вектора, його абсолютної величини. 

7.                 Додавання і віднімання векторів.  Поняття вектора з'явилося в роботах німецького математика XIX ст. Г. Грассмана та ірландського математика У. Гамільтона. Згодом воно було охоче сприйняте багатьма математиками і фізиками. В сучасній математиці це поняття відіграє дуже важливу роль.

Абсолютна величина вектора

                         AB = xAB2 + yAB2 +zAB2        величина вектораАбсолютна

Напрямленість векторів

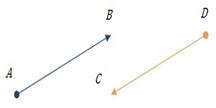•Вектори          називають протилежно напрямленими, якщо протилежно напрямлені півпрямі AB і CD .

                                                                                               •Вектори         і

називають співнапрямленими,  

якщо співнапрямлені півпрямі AB і CD.

Рівні вектори

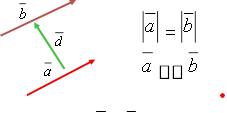• Рівні вектори – це вектори, що мають рівні абсолютні величини  та однаковий напрям.

Рівні вектори – це

                                                                a=b,                    вектори, що мають .

рівні координати

xa = xb, ya = yb, za = zb

Дії над  векторами

•За правилом

                        •Додавання              трикутника обидва

(правило вектора переносяться паралельно самим собі трикутника) так, щоб початок

одного з них збігався з кінцем іншого.

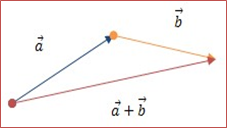•Вектор суми задається третьою стороною трикутника, що утворився, причому його початок збігається з початком першого вектора.

Дії над  векторами

•Додавання a(x_a; y_a;z_a)+b(x_b; y_b;z_b)=

= (xa +xb; ya + yb;za +zb)

•Закони додавання:

                                          •1) переставний                           ^a+b=b+a

                                         •2) _{сполучний}                  (a+b)+с=a+(b+c)

Дії над  векторами