«Логічні вирази та логічні операції. Таблиця істинності»

ПЛАН- КОНСПЕКТ УРОКУ

Учитель: Марина Порушник

Клас: 10 (профільний рівень)

Предмет: інформатика

Розділ «Основи алгоритмізації та об’єктно-орієнтованого програмування»

Тема 7. Алгоритми з розгалуженнями.

Урок № 32

Тема уроку:  «Логічні вирази та логічні операції. Таблиця істинності»

Мета уроку:

 Навчальна. Ознайомити учнів з логічними виразами та логічними операціями; навчити учнів записувати логічні вирази та знаходити їх значення за допомогою таблиць істинності.

Розвиваюча. Розвивати логічне  та алгоритмічне мислення,  самостійність, вміння застосовувати набуті знання до практичних завдань. Розвинути навички використання логічних виразів та логічних операторів.

Виховна. Виховувати наполегливість, естетичність у оформленні, грамотно висловлювати свої думки.

 

 

 

Обладнання уроку: персональні комп’ютери, мультимедійний проектор, зошити, схеми, підручники.

Тип уроку:  Комбінований

 Компетенції учнів на уроці:

Основні поняття	Основні знання	Основні уміння
Логічні операції. Прості та складені. Дії над логічними операціями. Таблиця істинності.	Знання з попередніх уроків. Що таке прості логічні операції. Які дії здійснюються над простими логічними операціями.	Уміти здійснювати логічні операції. Уміти будувати таблиці істинності. Використовувати логічні операції при розв’язуванні поставлених задач.

 

Основні етапи уроку:

№	Етап	К-сть хв.
I.	Організаційна частина	1 хв.
II.	Повідомлення  теми і мети уроку.	1 хв.
III.	Перевірка знань і умінь учнів з пройденного матеріалу (у вигляді тестів для всіх)	3 хв.
IV.	Актуалізація та корекція опорних знань.	10 хв.
V.	Ознайомлення з новим  матеріалом.	17 хв.
VI.	Засвоєння нових знань і вмінь.	10хв.
VII.	Підбиття підсумків уроку.	2 хв.
VIII.	Домашнє завдання.	1 хв.

Хід уроку:

 Етап I. Організаційний етап.

Що робить учитель	Що роблять учні
Вітається  з учнями.	Вітаються з вчителем.
Відмічає відсутніх.	Готуються до уроку.

Пам’ятка для учня!

1. Пригадайте правила техніки безпеки при роботі з ПК.
2. Через кожні 15 хв. виконуйте вправи для очей та для зняття м’язової втоми.

Форми навчання на цьому етапі: колективна.

Методи навчання на цьому етапі: словесний.

Засоби навчання на цьому етапі: учительський журнал.

 Етап II . Повідомлення  теми,  плану і мети уроку.

Що робить учитель	Що роблять учні
Учитель повідомляє тему уроку: «Логічні операції. Таблиця істинності». Метаю є навчитися здійснювати дії над логічними операціями та використовувати таблиці істинності. Повідомлення плану уроку.	Учні записують тему уроку і слухають учителя про подальший план уроку.

 

Форми навчання на цьому етапі: фронтальне навчання.

Методи навчання на цьому етапі: пояснювальний.

Засоби навчання на цьому етапі: в учнів зошит і ручка, в учителя- крейда і дошка.

Етап ІІI. Перевірка знань і умінь учнів з пройденого матеріалу.

Що робить учитель

Що роблять учні

Перевірка знань і умінь учнів буде здійснена за допомогою тестових завдань.  Учням буде запропоновано два види тестів для двох різних рівнів: Середній рівень (6 балів) Для цього рівня будуть надані тести в Microsoft Word з максимальною кількістю в 6 балів. Достатній рівень (9 балів) Для цього рівня будуть надані 10 тестів, спеціально розроблених в тестовому середовищі. Вибір рівня тестів із двох запропонованих учень буде здійснювати самостійно.

Кожен учень повинен вибрати рівень тестів із двох запропонованих, який на його думку найкраще йому підійде. Кожен окремо сідає за свій персональне комп’ютер і проходить тести.

 

Форми навчання на даному етапі: індивідуальна.

Методи навчання на даному етапі: традиційні (тестування).

Засоби навчання на даному етапі: персональні комп*ютери.

 

    Тести для повторення пройденого матеріалу з теми “ Логічні вирази та логічні операції.”

1. Логічним виразом називається такий вираз, внаслідок обчислення якого одержується логічне значення        або  

 

2. Складеним логічним виразом називається вираз, в якому використовуються логічні операції
3. До логічних операцій не належить:

     NOT

        AND

         OR

     ТOR

 

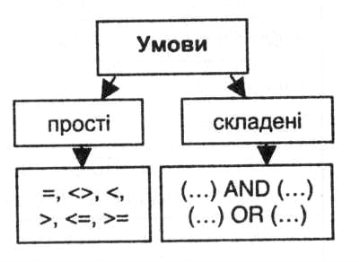
4. Логічні вирази в поділяються на 

     прості і складні;

     прості і складені;

     прості, складні і складені;

     лише прості.

5. Проста умова — це висловлювання, в якому

два вирази з’єднані знаком операції відношення;

дві або більше простих умов з’єднані знаками логічних операцій;

де не має логічних операцій.

 

6. Логічна операція or дає результат true тоді і тільки тоді, коли хоча б один операнд має значення  коли обидва операнди мають значення trueколи обидва операнди мають значення falseхоча б один операнд має значення trueхоча б один операнд має значення false
7.  3.1416 <= 3.1416 має значення TrueFalse

 

 

 

 

ВІДПОВІДІ

 

1. Логічним виразом називається такий вираз, внаслідок обчислення якого одержується логічне значення true або false («істина» або «хиба» ).
2. Простим логічним виразом називається вираз, який запи­суються за допомогою знаків співвідношень: <, >, <=, >=, = та <>..
3. До логічних операцій не належить ТOR
4. Логічні вирази в поділяються на   прості і складені.
5. Проста умова — це висловлювання, в якому

два вирази з’єднані знаком операції відношення;

6. Логічна операція or дає результат true тоді і тільки тоді, коли хоча б один операнд має значення true.
7. 3.1416 <= 3.1416 має значення True;

 

 

Для учнів які вирішили проходити середній рівень будуть надані тести в розробнику тестів.

 

 

Етап ІV.  Актуалізація та корекція набутих знань.

Що робить учитель

Що роблять учні

Даний етап призначений для корекції набутих знань за допомогою самих же учнів. Тобто задаються питання на які відповідь даватимуть не вчителі, а учні.    Вчитель запитує чи є питання в учнів по пройденій темі. Якщо є, то тоді відповісти на них учитель запропонує комусь із учнів, які претендують на оцінку від 9 до 12 балів. Якщо питань не має, то вчитель сам задає питання найвищої складності, відповідь на яке повинна бути максимально розгорнутою і повною.

Учні за бажанням виходить біля  дошки по черзі і отримують питання на 2 бали ( максимальна кількість питань – 2). Учень намагається якомога ширше і повніше дати відповідь на питання. Якщо потрібно, то і продемонструвати на ПК.

 

Форми навчання на даному етапі: індивідуальна.

Методи навчання на даному етапі: частково-пошуковий (або дослідницький).

Засоби навчання на даному етапі: комп’ютери, дошка, крейда.

 

 Питання, які задає учитель, якщо не має питань від учнів

1. Що таке логічні вирази? На які види вони поділяються? Наведіть приклади простих логічних виразів.

Варіант відповіді:

Крім арифметичних виразів, в алгоритмізації розглядається ще один тип виразів.

Він називається логічним. Логічними виразами називаються такі вирази, внаслідок обчислення яких одержуються логічні значення «true» або «false» («так» або «ні»).

Результатом виконання логічного виразу є логічне значення True(Істина) або False(Хибність). Операндами є дані тільки булевого типу.

Приклад:

3=4,

8>6.

Логічні вирази поділяються на прості та складені.

 

2. За допомогою чого записуються прості логічні вирази?  Виписати всі знаки співвідношення, що використовуються  у логічних виразах і навести приклади.

Простими логічнішії виразами називаються такі які записуються за допомогою знаків співвідношень «<», «>», «<=», «>=», «=» та «<>».

Операція	Опис операції
>	Більше ніж
> =	Більше або дорівнює
<	Менше ніж
<=	Менше або дорівнює
=	Дорівнює
<>	Не дорівнює

 

 

      3. Нехай змінна х має значення 0, а у - значен­ня 2. Визначити, які значення мають такі прості логічні вирази:

а) х < 5;

б) 5 > 7;

в) у = 2;

г) х + у >= 2 * х;  

д) х <> у.

Відповідь: логічні вирази а, в, г, д мають значення true, а вираз б — false.

 

4.Визначити, які значення виразів а)-д), якщо х = 2, а у — значення 0?

Відповідь: a) true, б) false, в) false, г) false, д) true.

          5. Усно. Чи істинний простий логічний вираз х > 10, якщо:

а) х=0 (відповідь: ні);

б) х=2; (ні) 

в) х=9; (ні)

г) х=5; (Ні)

д) х=15? (так)

 

 

Етап V. Ознайомлення з новим матеріалом.

Що робить учитель	Що роблять учні
Учитель ще раз повторює тему і починає ясно, доступно пояснювати новий матеріал. Акцентує увагу на важливому і надає можливість учням записати важливу інформацію. Для кращого сприйняття учнями матеріалу використовувати приклади і ілюстрації, таблиці і схеми.	Учні уважно слухають і записують найважливіше, що акцентує вчитель. Якщо щось не зрозуміло, то задають питання.

Форми навчання на даному етапі: колективна.

Методи навчання на даному етапі: пояснення.

Засоби навчання на даному етапі:ПК, зошити, дошка, учнівські предмети, підручники, схеми, ілюстрації .

ПОЯСНЕННЯ МАТЕРІАЛУ

Оскільки на минулому занятті було введено поняття логічної операції та ознайомлено учнів з визначенням простої логічної операції та символів за допомогою, яких вони записуються, то сьогодні основна увага буде приділена складеним логічним виразам  та таблицям істинності.

     Складеними логічними виразами називаються такі, які складаються з простих виразів, об’єднаних логічними операціями «and», «or», «not».

AND - логічне І, логічним множенням або кон'юнкцією, а результат операції - логічним добутком.

OR - логічне АБО, логічним додаванням або диз'юнкцією, а одержане складне висловлення - логічною сумою.

NOT - логічне за­перечення, НЕ.

При записуванні складених логічних виразів прості логічні вирази обов'язково беруться у круглі дужки!

Приклади.

1.Складена умова:

Not (А <= 3) - рівнозначне виразу А > 3.

З математики відомі такі записи:

 

2. х[а,b]

Спробуємо записати їх у вигляді логічних виразів

(х>=а) and (x<=b).

 

3. х[а,b]

(х<а) or (x>b)     або      not((x>=a) and (x<=b)).

 

Проілюструємо риклад

Складний логічний вираз

               (X>0) and (y=2*z) or (z+2=x+y) xor not(x>y)

Зверніть також увагу на те, що спочатку виконуються арифме­тичні дії, а вже потім порівняння одержаних результатів.

 

                         Пріоритет виконання операцій у логічних виразах:

 

Пріоритет операції	Операція
1	у дужках
2	/ , *
3	+, –
4	=, > , < , >= , <=, <>
5	Not
6	And
7	or, xor

У вказаному прикладі, спочатку обчислюються математичні вирази: у дужках виконаються операції „+” та „*”, потім обчислюються прості умови (виконуються операції “>”, “=” ), потім виконується логічна операція not, потім логічна операція and, потім логічні операції or та xor  у тому порядку, в якому вони записані.

Визначимо правила, за якими обчислюються значення складе­них логічних виразів.

Логічну функцію прийнято за­давати у вигляді таблиці істинності, вхідними значеннями якої є аргумен­ти функції (значення змінних для логічного виразу), а вихідними - відповідні значення логічної фун­кції.

0 -  False (Хибність)

1 - True (Істина)

Логічна операція AND (і, та, кожне, обидва)

Складена умова (проста умова 1) and ( проста умова 2) вірна, якщо вірні обидві простих умови. У інших випадках така складена умова невірна.

Таблиця істинності логічної операції and

Значення умови 1	Значення умови 2	Значення результату
TRUE	TRUE	TRUE
FALSE	FALSE	FALSE
FALSE	TRUE	FALSE
TRUE	FALSE	FALSE

Обчислюючи складену умову з логічною операцією and, можна не перевіряти значення другої умови, якщо одна з умов має значення FALSE . Весь вираз буде мати значення FALSE.

Операцію and називають логічним множенням.

Логічна операція OR (або, хоча б одне)

Складена умова (проста умова 1) or (проста умова 2) не вірна, якщо не вірні обидві простих умови.

У інших випадках така складена умова вірна.

Таблиця істинності логічної операції or

Значення умови 1	Значення умови 2	Значення результату
FALSE	FALSE	FALSE
TRUE	TRUE	TRUE
FALSE	TRUE	TRUE
TRUE	FALSE	TRUE

Обчислюючи складену умову з логічною операцією or, можна не перевіряти значення другої умови, якщо одна з умов має значення TRUE . Весь вираз буде мати значення TRUE.

 

 

Проілюструємо виконання логічних операцій AND і OR за до­помогою електричних схем:

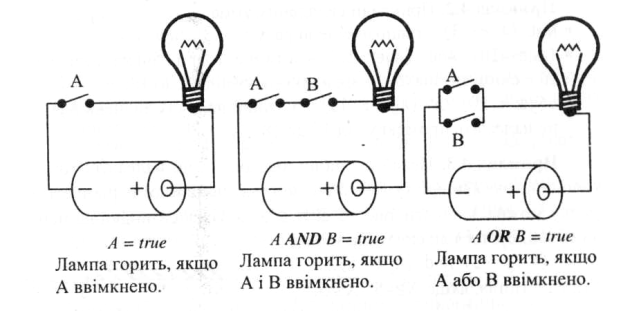
Ми вели розмову про обчислення значень логічних виразів.

Зрозумілим є запитання: «А де їх можна використовувати?»

По-перше, використання логічних виразів так, як і арифмети­чних, можливе в операторі присвоювання.

 

Наприклад:

logica_1:=a>b;

logica_2:=(N<=x) and (х<=М).

        

Умовою безпомилкового виконання таких операторів є співпадання типів, тобто змінні в лівій частині цих операторів повинні бути описані типом boolean.

По-друге, результат обчислення логічних виразів «true» та «false» можна ще трактувати як «так» та «ні». Це наводить на думку про використання логічних виразів для визначення оцінки деякої ситуації, що склалася, і прийняття рішення про те, що робити далі.

Приклад:

var X,Y:Integer;

         A:Boolean;

    Begin

         X := 5 ;

         Y := 2;

А:= X > Y;                 {Умова X>Y виконується, тому А отримує значення True}

А:= X < Y;                          {А = False}

А:= X - 4.5 < Y * 2;          {А = True }

 

VI . Засвоєння нових знань і вмінь.

Що робить учитель	Що роблять учні
Для кращого сприйняття учнями матеріалу потрібно використовувати приклади, ілюстрації, таблиці і схеми.  Учитель крім наведення своїх прикладів ставить перед учнями задачі або завдання, які їм потрібно самостійно розв’язати.	Учні за потребою повинні виходити до дошки для розв*язування завдань, або виконувати їх самостійно за наказом учителя.

Форми навчання на даному етапі: колективна.

Методи навчання на даному етапі: практична робота.

Засоби навчання на даному етапі:ПК, зошити, дошка, учнівські предмети, підручники.

Тепер розглянемо різні приклади застосування логічних виразів і логічних операцій. Продемонстуємо

Завдання 1.   Обчислимо значення виразу:

1. (2.9994 < 2.9995) And (3.1416 <= 3.1416)

Відповідь: має значення True;

2. Обчислимо  значення такої програми:

Const x=1; y=1;
 Var Z:Boolean;
Begin
 Z:=(x*x+y*y<4)or(x>=2)and(x<=4)and(y>=2)and(y<=4);
 writeln(z);
end.

Хід розв’язання:

Спочатку обчислюється значення виразу (x>=2)and(x<=4)and(y>=2)and(y<=4), будемо оператися на ті знання, які ми вже здобули на попередніх уроках, а потім значення виразу x*x+y*y<4. Але значення останнього виразу TRUE, тому незалежно від значення першого виразу весь вираз вірний.

Відповідь: TRUE

Завдання 2. Складемо таблицю істинності для логічної операції not

Значення умови 1	Значення результату

 

Відповідь:

Значення умови 1	Значення результату
FALSE	TRUE
TRUE	FALSE

Завдання 3. 

Заповнимо таблицю істинності, якщо А:=х>у, В:=х>0:

x	У	А	В	Not А	A Or В	A And В	Not (A And В)	Not А ОгВ
-3	4
3	5
-3	-5
5	3

 

Завдання 3

Запишіть умови з логічною операцією OR (відповідь записана у правому стовпчику таблиці.

Твердження	Умова
Хоча б одне з чисел X та Y додатне	(x>0)or(y>0)
Натуральне число X закінчується цифрою 2 або 3	(x mod 10=2)or(x mod 10=3)
Точка з координатами X та Y належить I або IIІ чверті координатної площини	(X>0)and(y>0)or(x<0)and(y<0)

Завдання 4.  Поясніть приклади обчислення логічних виразів з логічною операцією AND і знайдіть результат ( ВІДПОВІДІ вже дані в таблиці)

Приклади обчислення логічних виразів з логічною операцією OR

Програма	Пояснення	Результат роботи
Const X=10;  Var Z:Boolean; Begin  Z:=(x>2)and(x<5);  writeln(z); end.	X=10, тому x>2 вірно, а x<5 невірно, тому і весь вираз невірний.	FALSE
Const a=2; b=2;c=3;  Var Z:Boolean; Begin  Z:=(a>0)and(b>0)and(c>0);  writeln(z); end.	a=2; b=2; c=3, тому a>0 вірно, b>0 вірно, c>0 вірно, тому і весь вираз вірний.	TRUE

 

 Завдання 6. Завдання 1. Нехай змінна х має значення 0, а у - значен­ня 2. Визначимо, які значення мають такі прості логічні вирази:

а) х < 4;

б) 4> 7;

в) у = 2;

г) х + у >= 2 * х;  

д) х <> у.

Відповідь: логічні вирази а, в, г, д мають значення true, а вираз б — false.

Завдання 7. Визначимо, які значення виразів а)-д), якщо х = 2, а у — значення 0?

Відповідь: a) true, б) false, в) false, г) false, д) true.

 

VII. Підбиття підсумків уроку.

Отже сьогодні на уроці ми вияснили такі питання.

1. Для чого використовують логічні вирази?

2. Що таке простий логічний вираз?

3. Що таке складений логічний вираз.

4. Які є операції порівняння між величинами?

5. Для чого використовуються таблиці істинності.

І також навчилися розв*язувати певні задачі з логічними виразами.

Домашнє завдання.

1. Повторити все пройдене на сьогоднішньому уроці.
2. Вивчити і усвідомити основні поняття.
3.  Чи буде хибним вираз х >= 10, якщо:

х=1 (відповідь: так); б) х=3; в) х=10; г) х=12; д) х=25?

4) Встановити чи є істинними такі твердження:

• 5665 >555 (False);
• Вкажіть приорітет виконання дій у виразі (X>0) and (y=2*z) or (z+2=x+y) xor not(x>y)