Математична статистика

Математична статистика. Підготуваластудентка 1 курсу СО з.ф. Ткач Оксана

СТАТИСТИКА-ЦЕ НАУКА , ЯКА ВИВЧАЄ, ОБРОБЛЯЄ Й АНАЛІЗУЄ КІЛЬКІСНІ ДАНІ ПРО НАЙРІЗНОМАНІТНІШІ МАСОВІ ЯВИЩА В ЖИТТІ. Друга ріка- Математика

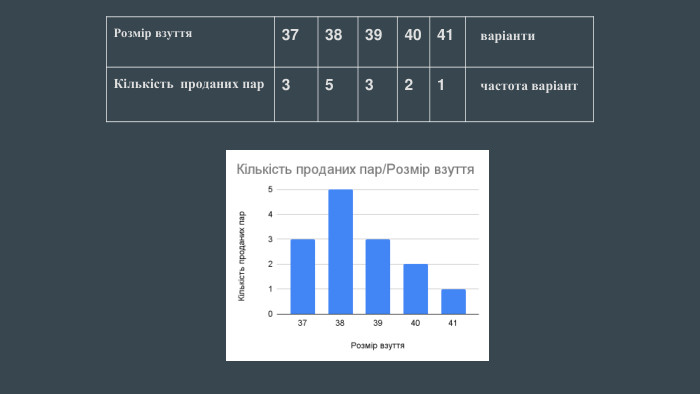
МАТЕМАТИЧНА СТАТИСТИКА-ЦЕ РОЗДІЛ МАТЕМАТИКИ, ЯКИЙ ВИВЧАЄ МАТЕМАТИЧНІ МЕТОДИ ОБРОБКИ Й ВИКОРИСТАННЯ СТАТИСТИЧНИХ ДАНИХ ДЛЯ НАУКОВИХ І ПРАКТИЧНИХ ВИСНОВКІВ.

Основні поняття математичної статистики. Сукупність – це множина об'єктів (елементів сукупності), які мають загальну властивість. Об'єм сукупності – це число елементів сукупності. Генеральна сукупність – найбільша сукупність, яка об’єднує всі елементи, що мають хоча б одну загальну властивість. Вибіркова сукупність (вибірка) – це частина генеральної сукупності, яка обрана для вивчення. Варіанта – це значення величини Х для окремого елемента вибірки.

Оцінки (вибіркові оцінки) статистичних характеристик – це значення досліджуваної випадкової величини, що отримані при вивченні вибіркової сукупності і які використовують замість істинних значень статистичних характеристик генеральної сукупності.

ВИДИ ОЦІНОК: Точкова оцінка статистичної характеристики – це чисельне значення оптимальної оцінки. Надійна оцінка, або інтервальна оцінка – це визначення надійного інтервалу, у який істинне значення статистичної характеристики генеральної сукупності попадає з деякою імовірністю α. Її зазвичай називають надійною ймовірністю або коефіцієнтом довіри. Величину p=1-α називають рівнем значущості відхилення оцінки або просто рівнем значущості.

Точкові оцінки1. Оптимальна вибіркова оцінка математичного сподівання величини X (середнє вибіркове)

2. Оптимальна вибіркова оцінка дисперсії величини X

3. Вибіркова оцінка середнього квадратичного відхилення величини XПохибка середнього

Методика надійного (інтервального) оцінювання математичного сподівання випадкової величини за вибіркою. Надійний інтервал для статистичної характеристики - це випадковий інтервал, границі якого повністю визначаються значеннями досліджуваної величини у вибірці, що вивчається, та який із заданою ймовірністю накриває істинне значення цієї статистичної характеристики.

Для обчислення границь надійного інтервалу для математичного сподівання нормально розподіленої випадкової величини Х можуть використовуватися різні формули залежно від того, відомим або невідомим є значення дисперсії D(X). При n≥30 вибіркову оцінку дисперсії можна приймати як істинне значення дисперсії, тобто вважати величину D(X) відомою. У цьому випадку надійний інтервал для М(Х) обчислюється за такою формулоювеличину t(α) знаходять за таблицею значень функції Лапласа, виходячи з умови

Якщо дисперсія невідома та n<30, то при визначенні надійного інтервалу для М(Х) використовують таку формулу k - число ступенів свободи (k = n – 1) t(, k) - коефіцієнт Стьюдента

{CD54 C138-C5 C2-41 EC-ACAE-B94 C3 C5 F6 E5 E}Розмір взуття3738394041 варіанти. Кількість проданих пар 35321 частота варіант

Застосування математичної статистики. Математична статистика має широкий спектр застосувань, включаючи:• Наукові дослідження: Аналіз експериментальних даних, виявлення закономірностей і формулювання висновків.• Економіка: Прогнозування економічних тенденцій, аналіз ринкових даних та оцінювання економічної політики.• Бізнес: Ухвалення рішень на основі даних, маркетинг, управління ризиками та прогнозування попиту.• Медицина: Оцінка ефективності лікування, діагностика захворювань та прогнозування ризиків для здоров'я.• Інженерія: Аналіз даних сенсорів, надійності систем і управління процесами.

ВИСНОВОКМатематична статистика є потужним інструментом для аналізу та інтерпретації даних. Вона надає ряд методів для отримання значущої інформації з вибірок та узагальнення висновків на популяції. Математична статистика відіграє важливу роль у багатьох сферах людської діяльності, допомагаючи приймати обґрунтовані рішення та покращувати наше розуміння світу.

ДЯКУЮ ЗА ВАШУ УВАГУ!