Презентація : „Застосування визначеного інтеграла“. 11 клас.
Про матеріал
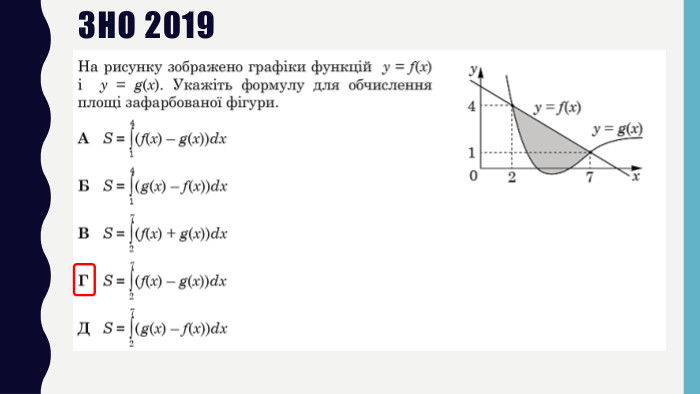
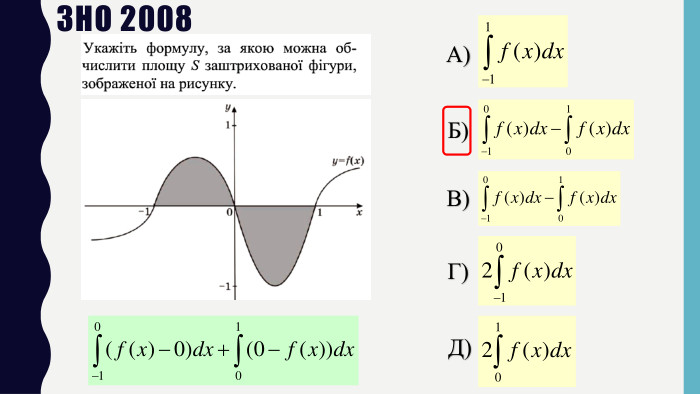
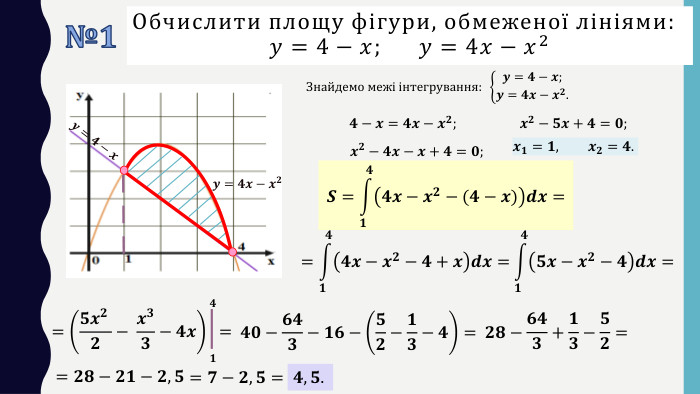
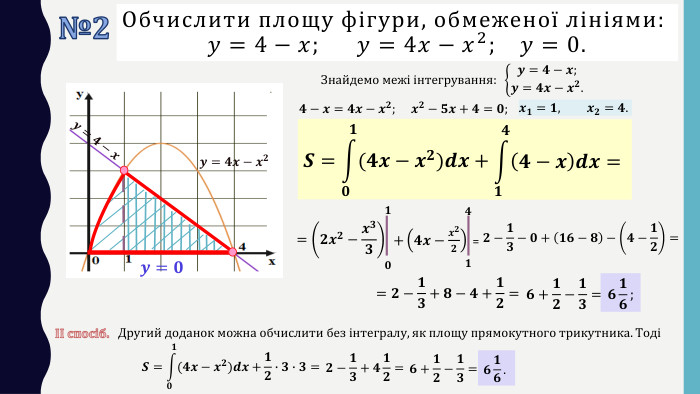
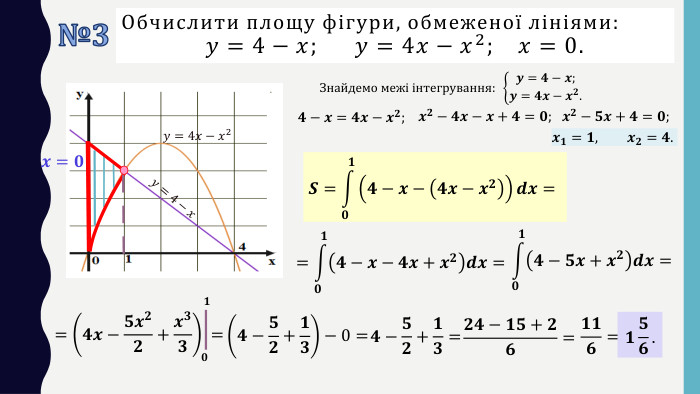
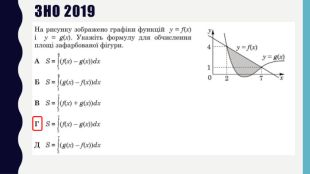
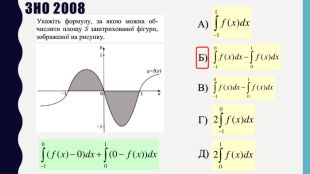
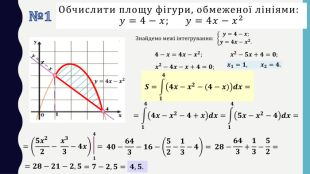
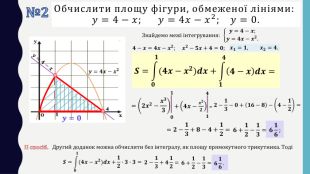
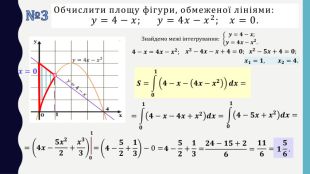
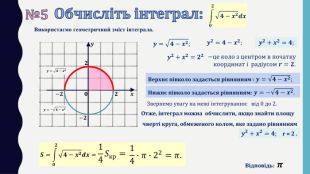
Презентація до уроку в 11 класі: „ Застосування визначеного інтеграла“. На уроці формуємо вміння обчислювати площі плоских фігур за допомогою визначеного інтегралу. На прикладі одного завдання, трохи змінюючи умову, показуємо учням, що фігура значно змінюється і спосіб обчислення також. Отже, треба бути уважними до умові завдання. Розв’язуємо також завдання на застосування геометричного змісту інтеграла і завдання ЗНО (НМТ) з даної теми. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
-
Дякую за роботу!


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку