Математична статистика.Генеральна сукупність і вибірка.

Генеральна сукупність і вибірка. Вибірковий метод“Методи математичної статистики” ДФКСКопиленко Л. М.м. Дніпро2023

Вибірковий метод у статистиці

Предмет і задачі математичної статистики.Імовірнісні характеристики більшості випадкових явищ (подій, величин, процесів), які зустрічаються на практиці, невідомі. Оцінити їх можна дослідним шляхом.

Математична статистика. Математична статистика - це прикладна математична дисципліна, яка досліджує масові випадкові явища і встановлює закономірності, яким вони підпорядковані, на базі вивчення методами теорії Ймовірностей статистичних даних - результатів спостережень або дослідів.

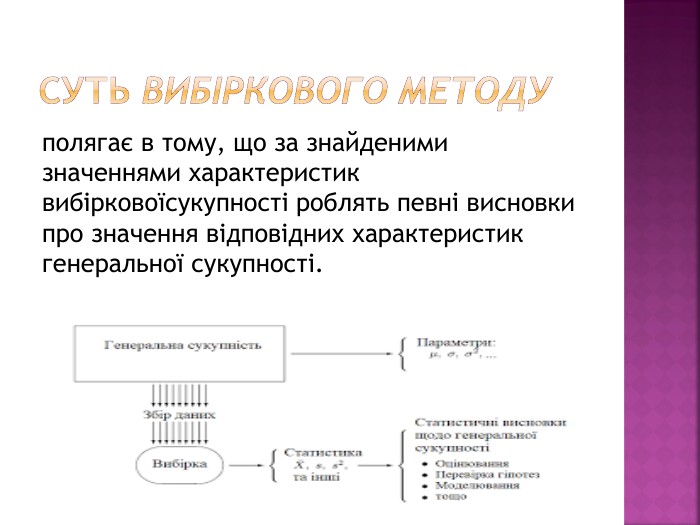
Основними задачами математичної статистики є1) розробка методів збору і систематизації статистичних даних, одержаних в результаті спостережень або спеціально поставлених експериментів;2) розробка методів аналізу статистичних даних залежно від мети досліджень. Сюди входять: оцінка ймовірності події; знаходжен-ня функції розподілу випадкової величини; оцінка параметрів розподілу;перевірка правдоподібності припущень про закон розподілу випадкової величини, про форму зв'язку міжвипадковими величинами або про значення параметра, який оцінюють.

Поняття генеральної сукупності та вибірки. Сукупність (множину) однорідних об'єктів, що об'єднані якою-небудь загальною кількісною або якісною ознакою, називають статистичноюсукупністю. Об'єкти, що утворюють, статистичну сукупність, називають її одиницями або елементами.

Якщо кількість елементів сукупності, яку вивчають, досить велика і обстежити їх усіх важко або неможливо, то вибирають яким-небудь способом із усієї сукупності обмежене число об'єктів і обстежують тільки їх.

Вибірковою сукупністю (вибіркою)називають сукупність випадково взятих об'єктів.

Генеральною називають сукупність об'єктів, з якої зроблено вибірку. Об'ємом сукупності (вибіркової абогенеральної) називають кількість її об'єктів.

Суть вибіркового методуполягає в тому, що за знайденими значеннями характеристик вибірковоїсукупності роблять певні висновки про значення відповідних характеристик генеральної сукупності.

Репрезентативніть вибірки. Щоб за даними вибірки можна було робити правильні висновки про генеральну сукупність,необхідно, щоб елементи вибірки правильно її представляли, тобто щоб вибірка була репрезентативною(представницькою). Вибірка буде репрезентативною, якщо вона випадкова.

Випадкова вибірка. Вибірка називається випадковою, якщо із генеральної сукупності елементи відбираються навмання,тобто будь-який її елемент з однаковою ймовірністю може потрапити у вибіркову сукупність.

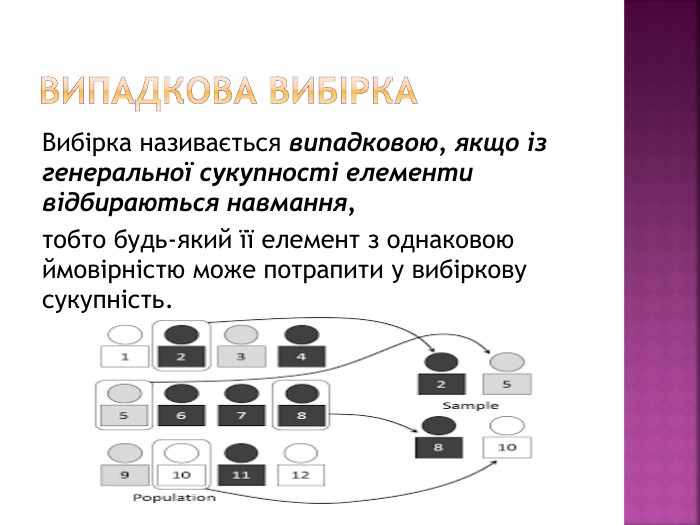
Розрізняють два типи випадкових вибірок: Вибірка називається повторною,якщо з генеральної сукупності відбирають будь-який елемент, фіксують значення ознаки, яку вивчають, а потім повертають цей елемент назад, у генеральну сукупність, і відбирають наступний елемент. Отже, при повторному відборі один і той самий елемент може потрапити у вибірку декілька разів. Вибіркат називається безповторною, якщо відібрані елементи назад у генеральну сукупність не повертаються.

Випадкова величина XЯкщо досліджується випадкова величина X, яка спостерігається в деякому досліді, то генеральною сукупністю називають множину всіх її можливих значень, а вибіркою - результат скінченої кількості спостережень цієї величини.

Об'єм вибірки. Набір значень ξ1, ξ2 ,…, ξn випадкової величини X, одержаних на практиці в результаті п незалежних послідовних дослідів,проведених в однакових умовах, називають вибіркою об'єму п. Вибірку ξ1, ξ2 ,…, ξn можна розглядати як послідовність незалежних в сукупності випадкових величин, розподіл кожної з яких збігається з розподілом досліджуваної випадкової величини X.

Статистичні методи опису результатів спостережень. Нехай із генеральної сукупності випадкової величини X взята вибірка об'єму п: ξ(1), ξ(2) ,…, ξ(n). Спосіб запису вибірки, за яким її елементи впорядковуються за величиною, тобто записуються у вигляді послідовності ξ(1), ξ(2) ,…, ξ(n), де ξ(1)≤ξ(2)≤…≤ξ(n), називається варіаційним рядом. Різниця між найбільшим і найменшим елементами вибірки ξ(n)-ξ(1)=ω називається розмахом вибірки.

Нехай варіаційний ряд містить k різних елементів х1, х2, …, хк, причому х1 повторюється n1 разів, х2 -п2 разів, ..., xk - пк разів. Тоді, елемент хi називається варіантою, число пi - його частотою, а відношення пi /п = wi - відносною частотою (і = 1..к).

Статистичний розподіл частот. За значеннями варіант, частот і відносних частот можна побудувати таблиці , які називають відповідно статистичними розподілами (рядами) частот і відносних частот або статистичними розподілами вибірки.

Якщо досліджувана випадкова величина X дискретна, то для графічного зображення статистичного розподілу вибірки використовують полігон частот (або відносних частот). Полігоном частот називають ламану, відрізки якої сполучають точки (хi;пi) на координатній площині Охп. Полігоном відносних частот називають ламану, відрізки якої сполучають точки (xi,wi) на координатній площині Ox. W.

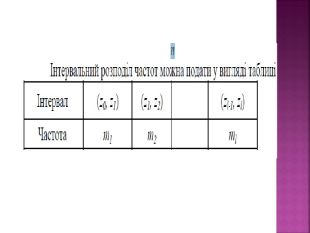
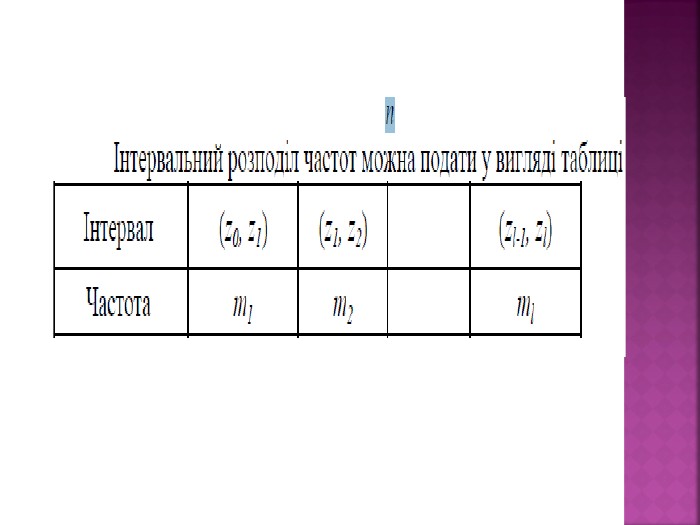
Для вибірки з неперервного розподілу або для вибірки великого об'єму з дискретного розподілу використовують представлення її у вигляді інтервального {групованого) статистичного ряду. Для його побудови потрібно інтервал, який містить всі елементи вибірки розбити на декілька часткових інтервалів довжиною h і знайти для кожного інтервалу його частоту ті - суму частот варіант, які потрапили в і-й інтервал (варіанта, яка збіглася з верхньою межею інтервалу відноситься до наступного інтервалу), або відносну частоту - wi =N mi

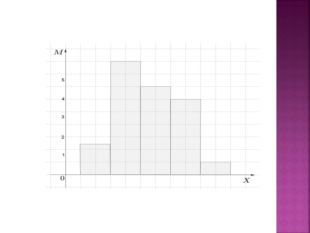
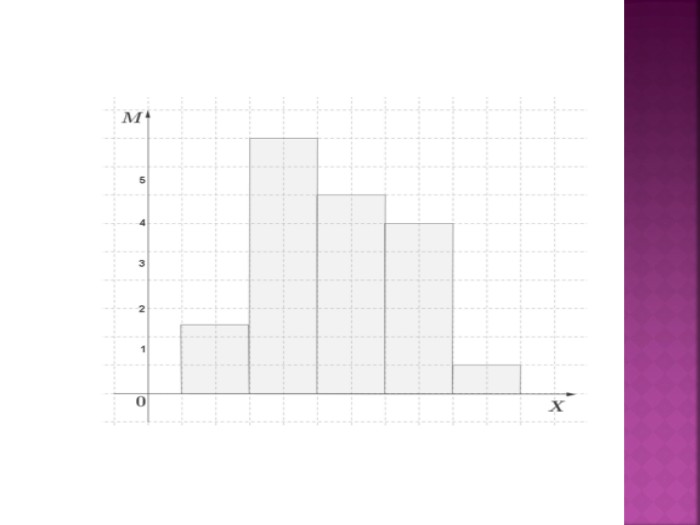
Для графічного зображення інтервального статистичного ряду будують гістограму частот (відносних частот) - східчасту фігуру, яка складається з прямокутників, основами яких є часткові інтервали довжиною h, а висоти дорівнюють mi/h. Величину mi/h називають щільністю частоти. Аналогічно будується гістограма відносних частот. Висоти прямокутників у цьому випадку дорівнюють wi/h. Величину wi/h називають щільністю відносної частоти.

Числові характеристики вибіркового розподілу. Розглянемо закон розподілу ДВВ X ,побудований за вибіркою із генеральної сукупності ВВ X:

Числові характеристики. Числові характеристики цього вибіркового розподілу називаються вибірковими {емпіричними) числовими характеристиками. Вибіркові числові характеристики є характеристиками даної вибірки і не є характеристиками генеральної сукупності. До числових характеристик вибірки відносяться: вибіркова середня, вибіркова дисперсія, вибіркове середнє квадратичне відхилення та ряд інших значень.

Вибірковою середньою. Вибірковою середньою хв називають середнє арифметичне елементів вибірки:

Вибіркова дисперсія. Вибірковою дисперсією Dв називають середнє арифметичне квадратів відхилень елементів вибірки від їх середнього значення хв :

Середнє квадратичне відхилення. Вибірковим середнім квадратичним відхиленням називають корінь квадратний з вибіркової дисперсії:

Мода і медіана. Вибірковою модою М*о називають варіанту, яка має найбільшу частоту. Вибірковою медіаною Ме називають число, яке ділить статистичний ряд на дві частини, рівні за кількістю варіант. Якщо число варіант непарне, тобто k = 2т + 1, то Ме =хт +1. При парному k = 2т медіана Ме =½ (хт +хт +1).

Середнє абсолютне відхилення. Середнім абсолютним відхиленням Q називають середнє арифметичне абсолютних величин відхилень елементів вибірки від вибіркової середньої:

Коефіцієнт варіаціїКоефіцієнтом варіації V1 (за середнім абсолютним відхиленням) називають визначене в процентах відношення середнього абсолютного відхилення до вибіркової середньої:

Зауваження. При обчисленні числових характеристик вибірки, заданої інтервальним статистичним рядом, в якості варіант беруть середини часткових інтервалів (усереднені варіанти).

Приклад Записати у вигляді варіаційного і статистичного рядів вибірку 7, 2, 8, 5, 5, 8, 7, 5, 8, 5. Визначити розмах вибірки та обчислити її вибіркову середню, вибіркову дисперсію і вибіркове середнє квадратичне відхилення так як на малюнку.

Розв'язання Об'єм вибірки n = 10. Впорядкувавши елементи вибірки за величиною, одержимо варіаційний ряд: 2, 5, 5, 5, 5, 7,7, 8, 8, 8. Різними в даній в даній вибірці є елементи х1 =2, х2= 5, х3 = 7, х4 =8. Отже, статистичний ряд вибірки такий:

Розмах вибірки ω = 8-2=6. Вибіркова середня x. B = 0,1 • (2 • 1 + 5 • 4 + 7 • 2 + 8 • 3) = 6 ; вибіркова дисперсія DB = 0,1• (4•1 + 25•4 + 49•2 + 64•3)-36 = 3,4; вибіркове середнє квадратичне відхилення σв = 3,4 =1,84.

Висновки Смислове значення середнього квадратичного відхилення таке саме, як і лінійного відхилення: воно показує, на скільки в середньому відхиляються індивідуальні значення ознаки від їх середнього значення.  Чим більший коефіцієнт варіації, тим менш однорідна сукупність і тим менш типова середня для даної сукупності. Встановлено, що сукупність кількісно однорідна, якщо коефіцієнт варіації не перевищує 33%.