Презентація "Найбільше і найменше значення функції на відрізку. Задачі на максимум і мінімум"
Про матеріал
В презентації описано теоретичний матеріал з теми "Найбільше і найменше значення функції на відрізку", вказано алгоритм дослідження функції на знаходження найбільшого і найменшого значень функції на даному відрізку. Запропоновано практичні завдання. Наведено приклади текстових задач на максимум і мінімум. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


![Рис. 1 Рис. 2 Розглянемо рисунки 1 і 2, на яких зображено графіки функції у = f(x) і у = g(x), заданих на відрізку [а; b]. Функція у = f(x) зростає, а функція у = g(x) спадає. На відрізку [а; b] найменше значення функції у = f(х) дорівнює f(a), а найменше значення функції у = g(x) дорівнює g(b). Відповідно найбільші значення цих функцій на даному відрізку дорівнюють f(b) та g(a). Отже, якщо функція неперервна і зростає (спадає) на деякому відрізку, то найбільше і найменше значення функція набуває на кінцях цього відрізка Рис. 1 Рис. 2 Розглянемо рисунки 1 і 2, на яких зображено графіки функції у = f(x) і у = g(x), заданих на відрізку [а; b]. Функція у = f(x) зростає, а функція у = g(x) спадає. На відрізку [а; b] найменше значення функції у = f(х) дорівнює f(a), а найменше значення функції у = g(x) дорівнює g(b). Відповідно найбільші значення цих функцій на даному відрізку дорівнюють f(b) та g(a). Отже, якщо функція неперервна і зростає (спадає) на деякому відрізку, то найбільше і найменше значення функція набуває на кінцях цього відрізка](/uploads/files/2624350/353080/406789_images/2.jpg)
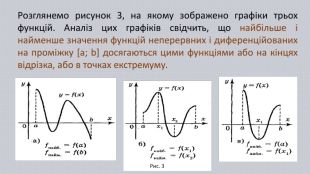
![Рис. 3 Розглянемо рисунок 3, на якому зображено графіки трьох функцій. Аналіз цих графіків свідчить, що найбільше і найменше значення функцій неперервних і диференційованих на проміжку [а; b] досягаються цими функціями або на кінцях відрізка, або в точках екстремуму. Рис. 3 Розглянемо рисунок 3, на якому зображено графіки трьох функцій. Аналіз цих графіків свідчить, що найбільше і найменше значення функцій неперервних і диференційованих на проміжку [а; b] досягаються цими функціями або на кінцях відрізка, або в точках екстремуму.](/uploads/files/2624350/353080/406789_images/3.jpg)

![Якщо функція у = f(x) неперервна на відрізку [а; b] і має похідну в кожній внутрішній точці цього відрізку, то для знаходження найбільшого і найменшого значень функції на відрізку [а; b] потрібно:1) знайти похідну функції,знайти критичні точки функції,вибрати критичні точки, які належать даному відрізку,4) обчислити значення функції у вибраних критичних точках і на кінцях відрізка,5) із знайдених значень вибрати найбільше і найменше. Якщо функція у = f(x) неперервна на відрізку [а; b] і має похідну в кожній внутрішній точці цього відрізку, то для знаходження найбільшого і найменшого значень функції на відрізку [а; b] потрібно:1) знайти похідну функції,знайти критичні точки функції,вибрати критичні точки, які належать даному відрізку,4) обчислити значення функції у вибраних критичних точках і на кінцях відрізка,5) із знайдених значень вибрати найбільше і найменше.](/uploads/files/2624350/353080/406789_images/5.jpg)
![fнайб. = f(-2)=-4; fнайм. = f(0) = -8.2) Знайдіть найбільше і найменше значення функції f(x) = х2+8х−1 на відрізку [-3; 0]. fнайб. = f(2) = f(-1)=5; fнайм. = f(1) = 1.1) Знайдіть найбільше і найменше значення функції f(x)=х3-3х+3 на відрізку [-1; 2]. fнайб. = f(-2)=-4; fнайм. = f(0) = -8.2) Знайдіть найбільше і найменше значення функції f(x) = х2+8х−1 на відрізку [-3; 0]. fнайб. = f(2) = f(-1)=5; fнайм. = f(1) = 1.1) Знайдіть найбільше і найменше значення функції f(x)=х3-3х+3 на відрізку [-1; 2].](/uploads/files/2624350/353080/406789_images/6.jpg)