"Математичні диктанти"

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

МАТЕМАТИЧНІ ДИКТАНТИ

АЛГЕБРА 7 КЛАС

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Підготувала вчитель математики

                                                   Низівської ЗОШ І-ІІІ ст.

                                                       Назаренко Ольга Іванівна

 

 

 

 

Математичні диктанти – добре  відома  форма  контролю знань , яка дає можливість одночасно і за короткий термін перевірити знання учнів усього класу. Завданням  математичного диктанту є повторення та засвоєння попереднього матеріалу, актуалізація  й оцінювання рівня  вивченого матеріалу.

Диктант триває, як правило, 10 – 15 хв. Перевага диктантів перед іншими видами навчальної діяльності полягає в тому, що всі учні класу виконують його одночасно, а тому у них формується зосередженість, розвивається увага та швидкість обчислювальних на­вичок.

  Важливо правильно провести диктант і організувати  його  перевірку. Результати математичних диктантів дають надійну інформацію про рівень засвоєння учнями нового матеріалу та попередньо вивченого. За результатами учитель має можливість своєчасно заповнити прогалини в знаннях учнів

 Варіанти  проведення математичних диктантів можуть бути такі:

1) учитель диктує приклади (рівняння, за­дачі...), а учні записують лише відповіді. Така форма роботи дає змогу навчати дітей працювати в загаль­ному ритмі, однаковому для всього класу;

2) хтось із учнів диктує завдання, а решта записують відповіді. Така форма роботи також учить працювати в загальному темпі (але темп більш уповільнений). Диктувати завдання доцільніше обирати учня, котрий має середній темп роботи;

3) на дошці записані завдання (на картці, у зошиті...) або у вигляді презентації , а діти фіксують лише відповіді. Така фор­ма роботи допомагає продуктивно дібрати оптимальне індивідуальне навантаження для кожного учня. До­вантажити тих, у кого темп роботи вище середнього, і дозволити працювати в уповільненому темпі учням з низьким темпом роботи.

Для учнів 7 класу я розробила  диктанти з алгебри,які використовую в своїй практиці. Їх можна також  використовувати при повторенні вивченого матеріалу.

Математичний диктант на тему

«Лінійне рівняння з однією змінною»

 

1. Яке рівняння називають рівнянням з однією змінною ?

2. Що означає розв’язати рівняння ?

3. Що називають коренем рівняння ?

4. Скільки  коренів може мати рівняння з однією змінною ?

5. Від чого залежить кількість коренів в лінійному рівнянні з однією

змінною ?

6. Сформулюйте основні властивості рівнянь.

Завдання по варіантах

7. Розв’яжіть рівняння  2х+5=18.         [ 3х-5=22    ].

 

8. Розв’яжіть рівняння 2(5х-1) =6,5.     [ 5(4х-2)=0,92 ].

 

9. Розв’яжіть рівняння  а²-5= -17.          [ х²- 8= -17   ].

 

10. Розв’яжіть рівняння  (5х-8)(3х+27)=0.    [ (4х-1,6)(8+х)=0    ].

 

11. Розв’яжіть рівняння  (18х-15)-(9+11х)= -3х.       [  26-4х=3х-7(х-3)   ].

 

12. Розв’яжіть рівняння  -.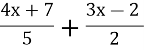

 

                                    [    ].

 

 

 

 

 

 

Математичний диктант на тему

« Тотожно рівні вирази. Тотожності » -7 клас

1. Записати , який вираз називають виразом зі змінними ?
2. Від чого залежить значення виразу зі змінними ?

3. Які вирази називають тотожно рівними ?

4. Що називають тотожністю ?
5. Які тотожні перетворення виразів вам відомі ?
6. Які прийоми використовують для доведення тотожностей ?

Завдання по варіантах

7. Знайдіть значення виразу х+3, 2, якщо  х= -6; 8; 8,2;  -3;  1,9.

 [ х = -5,4; 6,4;  -3,2;  1 ].

 

8. Виконайте тотожні перетворення виразу    2х+3х+4у-5у .  

         [ 3а + 5в - 2а-7в ].

 

9. Спростіть вираз    2(х- у)+3(х+ у).      [3(х + у) -2(х - у) ].

 

10.  При яких значеннях а вираз 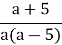    втрачає  зміст ? [  ] ?

 

 

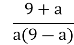11.  Доведіть тотожність  5в-(6в + а) - ( а - 6в) = 5в - 2а.

 

                                       [ 3а = 1,2 (а - 7) - 1,8( 3-а) + 13,8] .

 

 

 

 

 

 

 

 

 

Математичний диктант на тему

« Одночлени »

1. Які вирази називають одночленами ?
2. Запишіть приклад одночлена в стандартному вигляді.
3. Що називають коефіцієнтом одночлена ?
4. Які одночлени називають подібними ?
5. Що називають степенем одночлена ?
6. Який степінь одночлена, який є числом відмінним від нуля?

Завдання по варіантах

7. Зведіть одночлен до стандартного вигляду, укажіть його коефіцієнт і степінь 0,15 х³у⁴ *4х²у⁵ .     [  0,04х²у⁵ * 18х³у⁴   ] .

 

8. Знайдіть значення виразу: (3т⁴п)² *тп³ ,якщо  т = , п = 9. 

                                            [  (5х²у)³  * х³у² , якщо х =0,3; у = 0,2] .

 

9. Спрости вираз : 20х⁸ * (9х)².       [  12у⁶  * (-у⁵)⁴  ] .

 

10.   Замініть зірочки такими одночленами, щоб виконувалася рівність :

(*)²   (*)³ = 9х²у³с⁵.       [  (*)²   (*)³ =  -72х⁸у¹¹].

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математичний диктант на тему

«Многочлени»

1. Що називають многочленом ?
2. Який многочлен називають двочленом ?
3. Який  многочлен називають тричленом ?
4. Що називають подібними членами многочлена ?
5. Який многочлен називають многочленом стандартного вигляду ?
6. Що називають степенем многочлена стандартного вигляду ?

Завдання по варіантах

 

7. Знайди значення многочлена: 2х² + х +3 при х = 0,5.  

                                             [ у³ +5ху при х = 3, у = - 2  ] .

 

8. Зведи у многочленів подібні члени : 7х²у – 3ху² –х²у +2х²у – 4ху².

[ 5ху³ + 8х²у² – 2ху³ -4х²у² + 6 х²у² - 9+12].

 

9. Запиши  многочлен у стандартному вигляді:  2х²у² – ху³ – х⁴ – х²у² +ху³ +2х⁴+х⁵.    [ 5х * 2у² – 5х * 3ху –х²у + 6ху²] .

 

10.  Спростіть вираз: (2х + у) – (у -2х).  [ (3х - 4) + (3 -5х) ].

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математичний диктант на тему

«Додавання і віднімання многочленів»

1. Як розкрити дужки перед якими стоїть знак « + » ?
2. Як розкрити дужки перед якими стоїть знак « - » ?
3. Які доданки називаються подібними ?
4. Коли тотожність вважається доведена ?
5. Як додати многочлен ?
6. Як відняти многочлен ?

 

Завдання по варіантах

7. Знайди суму і різницю многочленів:  7х² – 5х + 3 і 7х² – 5.

                                                                    [3у² +7у -5 і 3у² +1 ].

 

8. Спростіть вираз:  (3х +10у) – (6х +3у) + (6у – 8х).                                 [ ( 2х – 11у)   - (12у +5х)+ (3х -17 у)].

 

9.Знайдіть :   1) А+В, якщо А =3х + 5; В = 5х – 16;

                                 2)А, якщо  В = х³ + 3х²у + у³; А+В = х³ + 6х²у – 2у³.

 

[ 1) А  - В, якщо  А =5х+1, В = 4х-4;

         2) В, якщо А = 2х² +х +3, А+В =2х+3 ].

 

          10.  Запишіть замість * такий  одночлен, щоб виконувалася рівність :

                      * . (х у - у²) = х³у – х²у².         [(х- у) . *  = х³у –х²у² ].

 

 

 

 

 

 

 

 

 

Математичний диктант на тему

« Множення многочлена на многочлен»

 

 

1. Запиши розподільний  закон множення.
2. Як помножити многочлен на многочлен ?
3. Запиши схему множення многочлена на многочлен.

 

Завдання по варіантах

 

4. Виконай множення: 1) (т + п) (а - 2); 2) (4т – п + 1) (х- у).    

 

                                    [ 1)  (3 - а) (в +с - 5);  2) (7а – 3в) (2а -5с) ].

 

 

5. Спрости вираз     1) 4 (х - 3) – 3 ( х + 4);    2)2х (х +2) – 5х (1 + х); 

                                          3) ( 5а²- 4в) *2в – (3а² – 2в)* 3в.

 

                            [  1)5(х + 2) – 6 (х - 2);    2) 3а (а - 1) – 4а (1 + а);

                                        3) (3х² – 4у) * 5у – (2х² -3у) * 3у].

 

         6.  За якого значення  х  значення даних виразів рівні :

                                         (х + 1)(10х - 3)  і  (5х + 1)(2х - 3)?   

                                       [ ( 5 + 3х) (4х -1)  і (2х + 7) (6х - 3)]?

 

 

7. Доведіть  тотожність : ( у - 1)(2 +у) – у² = у (3 – 2у) – 2 -2у +2у².

 

                     [ (а² - 7)(а + 2) – (2а - 1)(а - 14)+28 = а (а² + 22) ].

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математичний диктант на тему

« Розкладання многочлена на множники»

1. Що означає розкласти многочлен на множники ?
2.  Які відомі способи розкладання многочлена на множники ?
3. Яку властивість множення використовують при винесенні спільного множника за дужки ?
4. Як розкласти многочлен на множники способом групування ?

Завдання по варіантах

 

5. Розкладіть многочлен на множники: 9ав + 6а²в³; х + у +т (х + у).

[ 7т + тп + 7 + п;  3ву – 3в + 4ау -4а].

 

6. Спростіть і знайдіть значення виразу: 10,28х – х², якщо = 9,28. ).            [ х у + у² – 12х – 12у, якщо х = 10,8, у = - 8,8].

 

7. Винесіть спільний множник за дужки ?

 

1. 12а²в⁶ -24ав⁵ +6а³в⁴; 2) 2Х(а - в) + у (в-а).

 

        [ 1)15т²в⁷ -30 тв⁶ + 6т²в; 2) 3в (т - п) + а(п - т) ].

 

 

8. Розкладіть многочлен на множники способом групування:

1)5а – 5в + (а -в)т; 2) 6у + 42 + 7х + ху;                                             3)32ху² – 16ту² – 10у³ -24 тz ²- 15уz² + 48хz².  ).

 

     [ 1) 7х – 7у + (х -у)а ; 2) 7а + 49 + 14в + 2ав;                                                         

       3) 16ав² – 10с³ + 32ас² – 5в²с +кв² + 2кс²].

 

 

9. Розв’яжи рівняння: 1) 8у²  - 48у = 0;   2)18х – 4х²  = 0).

 

[ 9х² -72х = 0;   2) 15х – 4х² = 0].

 

 

 

 

 

Математичний диктант на тему

« Формули скороченого множення»

1. Запиши  формулу різниці квадратів двох виразів.
2. Чому дорівнює квадрат суми та квадрат різниці двох виразів ?
3. Чому дорівнює куб суми та куб різниці двох виразів ?
4. Який тричлен називають неповним квадратом суми виразів а і в ?
5. Який тричлен називають неповним квадратом різниці виразів а і в ?
6. Які відомі тобі способи розкладання многочлена на множники ?

Завдання по варіантах

 

7. Розкласти на множники:     4-х².         [у²  - 16х²].

 

8. Обчисли : 47²  - 37² .      [ 63² -23²].

 

9. Розв’яжи рівняння: (2п - 1)² – 25 = 0.        [  (3х +2)² – 16 = 0].

 

 

10.  Знайди значення виразу:  (63² - 27²) : (78² - 30²).

                                        [  ( 51,3² – 11,3²) : (113,9² – 73,9²)].

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математичний диктант на тему

«Системи рівнянь з двома змінними»

1. Яке рівняння називають лінійним рівнянням із двома змінними ?
2.  Що називають розв’язком рівняння із двома змінними ?
3.  Коли лінійні рівняння з двома змінними утворюють систему рівнянь ?
4.  Що називають розв’язком  системи рівнянь із двома змінними ?
5.  Що означає розв’язати систему рівнянь ?
6.  Які відомі тобі способи розв’язування систем рівнянь ?

Завдання по варіантах

7.  Чи є пара чисел  (5;2) розв’язком системи:

 

                  [ ].

 

8. Розв’яжи систему рівнянь способом підстановки:

          [ ].

 

 

9. Розв’яжи систему рівнянь способом додавання:

 

          [ ].