Конспект уроку "Різні способ розвязування квадратних рівнянь"
Міністерство освіти і науки, молоді та спорту України
Методична розробка уроку алгебри в 8 класі
Нестандартні способи
розв'язування квадратних рівнянь
Робота вчителя математики
Тарасівської ЗОШ І-ІІІступенів
Тодорової Надії Василіни.
с.Тарасівка. 2017
Нестандартні способи
розв'язування квадратних рівнянь
Мета уроку:
- Закріпити знання, вміння, навички учнів при розв'язуванні квадратних рівнянь;
- Розвивати логічне мислення, увагу, пам’ять, вміння спостерігати, порівнювати, узагальнювати та аналізувати математичні ситуації;
- Виховувати пізнавальну активність, самостійність, наполегливість в досягненні мети, інтерес до математики.
Графічний диктант
-
1. Квадратне рівняння – це рівняння виду
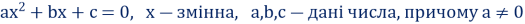 ;
;
-
2. Квадратне рівняння
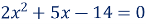 є зведеним;
є зведеним;
- 3. Якщо дискримінант квадратного рівняння дорівнює нулю, то рівняння має один безліч коренів;
-
4. Сума коренів рівняння
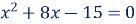 є число (-8);
є число (-8);
-
5. Корені рівняння

-
6. Рівняння 6

-
7. Значення виразу
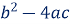 , де
, де 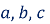 - коефіцієнти квадратного рівняння називається дискримінантом;
- коефіцієнти квадратного рівняння називається дискримінантом;
- 8. Квадратне рівняння, у якого принаймні б один з коефіцієнтів (b) або (с) дорівнюють нулю, називають неповним квадратним рівнянням;
-
9. Другим коефіцієнтом в квадратному рівнянні 3
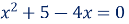 є число 5;
є число 5;
-
10. Пара чисел 2 і 4 є коренями рівняння
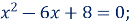
-
11. Коренями рівняння
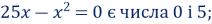
-
12. Формули розв'язування для квадратних рівнянь мають вигляд
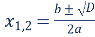
Наступний етап уроку розпочнемо словами У. У. Сойєра
„…людині, яка вивчає алгебру, часто корисно розв’язати одну й ту саму задачу трьома різними способами, ніж розв’язати три-чотири різні задачі. Розв’язуючи одну задачу різними способами, можна за допомогою порівнянь з’ясувати, який з них коротший і ефективніший. Так виробляється досвід.
Розвязування квадратних рівнянь в давнину
Необхідність розв'язувати рівняння не тільки першого, але і другого степеня ще в давнину була викликана потребою розв'язувати задачі, пов'язані із знаходженням площ земельних ділянок та земляними роботами військового характеру, а також з розвитком астрономії і самої математики. Квадратні рівняння вміли розв'язувати близько 2000 років до нашої ери. Правило розв'язування цих рівнянь, викладене у папірусах та клинописних текстах вавілонян та єгиптян, збігається з сучасним, проте невідомо, яким чином вони дійшли до цього. Незважаючи на високий рівень розвитку математики у давнину відсутні поняття від'ємного числа і загальні методи розв'язання квадратних рівнянь.
В одному з папірусів міститься завдання: «Знайти довжину сторін поля, що має форму прямокутника, якщо його площа 12, а ¾ довжини рівні ширині.»
Розв’язок:
Нехай довжина поля дорівнює х, тоді його ширина дорівнює ¾х, а площа дорівнює ¾х². Отримуємо квадратне рівняння
¾х² = 12.
У папірусі описано правило його вирішення. Треба розділити 12 на ¾.
Отримаємо х² = 16.
«Довжина поля дорівнює 4», - йдеться в папірусі.
Інший спосіб вирішення квадратних рівнянь описав аль-Хорезмі.
Він заснований на методі виділення повного квадрата.
Наприклад, в разі рівняння х² + 10х = 39
треба знайти число, додавши яке до лівої частини, отримаємо повний квадрат. Це число 25.
х² + 10х + 25 = 39 + 25;
(х + 5) ² = 64;
х + 5 = 8;
х = 3.
Аль-Хорезмі працював з позитивними числами, тому вказав тільки один корінь. Другий корінь знайдемо з рівняння х + 5 = - 8. Він дорівнює -13.
Властивості коефіцієнтів квадратного рівняння
Нехай дано квадратне рівняння ах2 + bх + с = 0, де
а ≠ 0. Якщо, а+ b + с = 0 (тобто сума коефіцієнтів дорівнює нулю), то х1 = 1, х2 = ![]() .
.
Доведення. Розділимо обидві частини рівняння на
а ≠ 0, отримаємо зведене квадратне рівняння
x2 + ![]() • x +
• x +![]() = 0.
= 0.
Згідно з теоремою Вієта x1 + x2 = - ![]() , x1x2 =
, x1x2 = ![]() .
.
За умовою а + b + с = 0, звідки b = -а - с. Таким чином,
x1 + x2 = ![]() = 1 +
= 1 + ![]() , x1x2 = 1•
, x1x2 = 1•![]() , тобто. х1 = 1 і х2 =
, тобто. х1 = 1 і х2 = ![]() .
.
Якщо в квадратному рівнянні a+c=b, то один з коренів дорівнює (-1),другий (- ![]() )
)
Приклад 1 : 5х2 - 8х + 3 = 0.
a = 5; b = - 8 c = 3.
а + b + c = 5 – 8 + 3 = 0, то х1 = 1; х2 = ![]()
Приклад 2: 5х2-6х-11=0.
а= 5; b =-6; с = -11.
а – b + c = 5 + 6 – 11=0, то х1 = - 1; х2 = - ![]()
Розв’язування рівнянь способом «перекидання» старшого коефіцієнта
Розглянемо квадратне рівняння ах2+ bх +с = 0, де а ≠ 0. Домножуючи обидві його частини на а, отримуємо рівняння а2х2 +аbх+ ас = 0. Нехай ах = у, звідки х = ![]() ; тоді приходимо до рівняння у2 + by + ас = 0, рівносильне даному. Його корені у1 і у2 знайдемо за допомогою теореми Вієта. Остаточно отримуємо х1 =
; тоді приходимо до рівняння у2 + by + ас = 0, рівносильне даному. Його корені у1 і у2 знайдемо за допомогою теореми Вієта. Остаточно отримуємо х1 = ![]() і х2 =
і х2 = ![]() . При цьому способі коефіцієнт а множиться на вільний член, як би «перекидається» до нього, тому його називають способом «перекидання». Цей спосіб застосовують, коли можна легко знайти корені рівняння, використовуючи теорему Вієта і, що найважливіше, коли дискримінант є точний квадрат.
. При цьому способі коефіцієнт а множиться на вільний член, як би «перекидається» до нього, тому його називають способом «перекидання». Цей спосіб застосовують, коли можна легко знайти корені рівняння, використовуючи теорему Вієта і, що найважливіше, коли дискримінант є точний квадрат.
Приклад: Розв’яжіть рівняння : 2х 2 - 11х +15 = 0.
Перекинемо коефіцієнт 2 до вільного члена
у 2 - 11у +30= 0.
то, за оберненою теоремою Вієта, отримуємо корені: 5; 6,
далі повертаємось до коренів даного рівняння: 2,5; 3.
Відповідь: 2,5; 3.
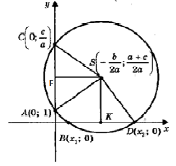 Розв’язання квадратних рівнянь за допомогою циркуля і лінійки
Розв’язання квадратних рівнянь за допомогою циркуля і лінійки
Розв’яжемо квадратне рівняння ![]() за допомогою циркуля лінійки
за допомогою циркуля лінійки
Припустимо, що шукане коло перетинає вісь абсцис в точках В(х1,0) і D(х2,0), де х1 і х2 - корені рівняння ах 2 + b х + с = 0, і проходить через точки ![]() на осі ординат. Тоді за властивістю січних маємо OB · OD = OA · OC, звідси
на осі ординат. Тоді за властивістю січних маємо OB · OD = OA · OC, звідси ![]()
Центр кола знаходиться в точці перетину перпендикулярів SF і SK, проведених в серединах хорд AC і BD, тому
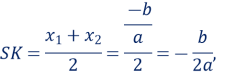
![]()
![]()
Отже, щоб розвязати рівняння за допомогою циркуля і лінійки:
1) побудуємо точки ( центр кола ) і А(0, 1);
2 ) проведемо коло з радіусом SA ;
3 ) абсциси точок перетину цього кола з віссю Ох є коренями початкового квадратного рівняння.
При цьому можливі три випадки .
-
1) Радіус кола більше ординати центра (AS > SВ , або R >
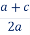 ), коло перетинає вісь Ох у двох точках У(х1,0) і D(х2, 0) , де х1 і х2 - корені квадратного рівняння ах 2 + b х + с = 0.
), коло перетинає вісь Ох у двох точках У(х1,0) і D(х2, 0) , де х1 і х2 - корені квадратного рівняння ах 2 + b х + с = 0.
-
2 ) Радіус кола дорівнює ординаті центра (AS = SB , або R =
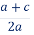 ), коло дотикається до осі Ох в точці В(х1,0), де х1 - корінь квадратного рівняння.
), коло дотикається до осі Ох в точці В(х1,0), де х1 - корінь квадратного рівняння.
- 3 ) Радіус кола менший ординати центра, коло не має спільних точок з віссю абсцис , у цьому випадку рівняння не має розв’язку.
![]()
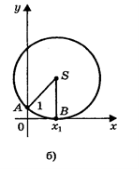
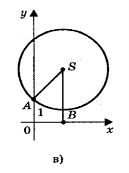
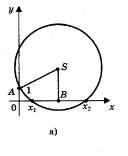
 Приклад: Розв’яжемо рівняння х2 - 2х - 3 = 0 Розв’язання. Визначимо координати центра кола за формулами:
Приклад: Розв’яжемо рівняння х2 - 2х - 3 = 0 Розв’язання. Визначимо координати центра кола за формулами:![]()
![]() =1;
=1;![]()
Проведемо коло радіуса SA , де А (0, 1).
Відповідь: х1 = - 1; х2 = 3.
Розв’язування квадратних рівнянь за допомогою номограми
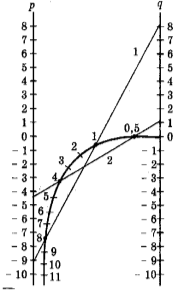 Це старий і незаслужено забутий спосіб розв'язання квадратних рівнянь, поміщений на с.83 «чотиризначний таблиць Брадіса»
Це старий і незаслужено забутий спосіб розв'язання квадратних рівнянь, поміщений на с.83 «чотиризначний таблиць Брадіса»
Приклади.
1. Для рівняння z2 - 9z + 8 = 0. Номограма дає корені z1 = 8,0 і z2 = 1,0
2. Розв’яжемо за допомогою номограми рівняння 2z2 - 9z + 2 = 0. Розділимо коефіцієнти цього рівняння на 2, отримаємо рівняння
z2 - 4,5z + 1 = 0.
Номограма дає корені z1 = 4 і z2 = 0,5.
Висновок:
дані прийоми розв’язання заслуговують на увагу, тому що їх не вивчають в шкільних підручниках математики;
оволодіння даними прийомами допоможе економити час і ефективно розв’язувати рівняння;
потреба у швидкому розв’язуванні обумовлена застосуваннями тестової системи вступних іспитів.
Закінчити речення
Сьогодні я дізнався(лась)…
Було цікаво…
Я поняв(ла), що…
Тепер я можу…
Я навчився(лась)…
У меня получилось…
Я попробую….
Мене здивувало…
Мені захотілось…
Домашнє завдання:
Який із відомих вам способів ви обрали б для розв’язання даних рівнянь. Розвяжіть рівняння різними способами (не повторюючись).
137х 2 + 20х – 157 = 0;
х2+6х+8=0;
0,5х²-2,5х-7=0;
3х²-14х+16=0;
4х2+9х+2=0.


про публікацію авторської розробки
Додати розробку
