Математичний маятник.Період коливань математичного маятника " 11 клас

Тема  Математичний маятник.Період коливань математичного маятника     11 клас

 Навчальна:  ввести поняття математичний маятник ; вивести рівняння коливального руху  та формулу періоду коливань математичного маятника; навчити застосовувати вивчене в знайомих і нових ситуаціях; формувати вміння застосувати одержані теоретичні знання під час розв’язування конкретних завдань.

 Розвивальна:  розвивати вміння систематизувати відомі фізичні факти, розвивати спостережливість, уміння встановлювати причинні зв'язки; формувати в учнів самостійну, творчу активність, ініціативу як стійкі якості особистості; виробляти вміння самостійно вчитися, поглиблювати або поповнювати знання; формувати  позитивні мотиви учбової діяльності, пізнавальний інтерес, бажання вчитися, позитивне ставлення до навчання.

Виховна: розвивати уявне й логічне мислення, інтерес до експерименту; виховувати навички індивідуальної і колективної роботи; виховувати інформаційну культуру .

Тип уроку: урок вивчення нового матеріалу.

Обладнання: мультимедійний проектор , комп'ютер, комп'ютерна презентація,

нитяний маятник, ,секундомір.

Структура уроку:

1. Актуалізація опорних знань

Тест – контроль (3 хв.)

2. Мотивація навчальних знань (1 хв.)
3. Пояснення нового матеріалу (17 хв.)
4. Закріплення нового матеріалу.

1. Лабораторний експеримент(5хв)
2. Розв’язування задач (9 хв.)

5.  Підсумок уроку (0,5 хв.)
6. Домашнє завдання (0,5 хв.)

Хід уроку:

1.Актуалізація опорних знань  Тест – контроль (3 хв.)

1. Мотивація навчальних знань (1 хв.)
2. Пояснення нового матеріалу (17 хв.)

5. Математичний маятник
Узагальнення та систематизація знань (розв’язування задач):

Щоб обчислити період коливань вантажу, що висить на нитці, необхідно трохи «ідеалізувати» задачу. По-перше, вважатимемо, що розміри вантажу набагато менші за довжину нитки, а нитка — нерозтяжна й невагома. По-друге, вважатимемо кут відхилення маятника досить малим (не більшим за 10—15°).

- Математичним маятником називається ідеалізована коли­вальна система без тертя, що складається з невагомої та не­розтяжної нитки, на якій підвішена матеріальна точка.

Розглянемо коливання математичного маятника. Для цього ві­зьмемо невелику, але досить важку, кульку й підвісимо її на довгу нерозтяжну нитку.

Розглядаючи коливання математичного маятника, ми дійдемо висновку, що причини, які зумовлюють вільні коливання, такі ж, як і у випадку пружинного маятника (див. рис. а — д):

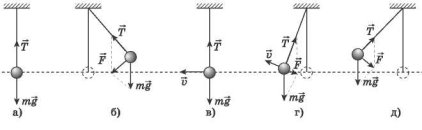
1)   дія на кульку сил, рівнодійна яких завжди спрямована в бік по­ложення рівноваги;

2)   інертність коливної кульки, завдяки якій вона не зупиняється в положенні рівноваги.

5.   Період коливань математичного маятника

Доведемо, що математичний маятник здійснює гармонічні ко­ливання.

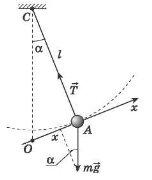
Запишемо рівняння другого закону Ньютона в проекції на вісь ОХ (див. рис): . Оскільки , то і ми дістаємо рівняння: , або . Значення можна розрахувати з трикутника ОАС — воно дорівнює від­ношенню катета ОА до гіпотенузи ОС. Якщо кути малі, , де — довжина нитки, а , де  x — відхилення кульки від положення рівноваги. Тому . Остаточно отримуємо: . Позначивши , маємо рівняння для вільних коливань математичного маятника: . Циклічна частота коливань математичного маятника: . Скориставшись співвідношенням , знайдемо формулу

для періоду коливань математичного маятника:

.

Період вільних коливань математичного маятника не залежить від його маси, а визначається лише довжиною нитки та прискорен­ням вільного падіння в тому місці, де знаходиться маятник.

Відомо, що в різних точках земної кулі прискорення вільного падіння різне. Воно залежить не лише від форми Землі, але й від наявності в її надрах важких (метали) або легких (газ, нафта) речо­вин. А отже, і період коливань маятника в різних точках буде різ­ним. Ця властивість використовується, зокрема, під час пошуків покладів корисних копалин.

2Запишіть рівняння коливань математичного маятника довжиною l =0,1 м, амплітуда коливань якого становить A = 11 см. Коливання починаються з амплітудної точки.

1. Як змінився: хід маятникових годин, привезених з Києва на наукову станцію в Антарктиді?
2. Яка з кульок, зображених на малюнку, може здійснювати коливання?
3. Коливання: вантажу на пружині описують рівнинним: х = 0,1sin0,51t. Визначте амплітуду, період, колову частоту й частоту коливань.
4. Яке відношення довжин двох математичних маятників, якщо один з них робить 31 коливання за той самий час, за який другий виконує 20 коливань? (Відповідь: довжина другого маятника більше у 2,4 раза.)

4 Підведення підсумків і повідомлення домашнього завдання. (Слайд 19)

Висновок: Сьогодні на занятті ми з вами розібрали основні поняття та закони з теми « Математичний маятник Період коливань .»; навчились застосувати одержані теоретичні знання під час розв’язування конкретних завдань.

Домашнє завдання: Вивчити конспект. Розібрати матеріал § 42-44 (Фізика 11 Коршак О.І)

1. Як зміниться період коливань маятника, якщо його перенести з повітря у воду?
2.  Написати рівняння гармонічного коливального руху за такими його характеристиками:
   
   а) амплітуда 5,5 см, період 1 хв, початкова фаза 30º;
   
   б) амплітуда 0,1 м, частота 10 коливань за 1 с, початкова фаза дорівнює нулю.