розв9язування задач з лойчним наванпненням

CaM6ip 2018

, вчитель вищот категорг•• навчально-виховного комплексу ”Середня школа l - l l - дошкльнии навчальнии заклад'

У цьому noci6HHkY' 3i6paH0 pek0MeHAalJii щодо роботи нал розв'язуванням задач з ,norit1HllM навантаженням, наведено зразки 3Micvy складання плану розв'язування i розв'язок а також конспектн Y'P0kiB з математики для YMHiB 1-4

Для використання вчителям початкових kJ1aciB, вихователям гпд

BCTY ll до програми MiHicTepcTBa науки i Укра\ни 2006 року з логјчним навагтгаженням починають вивчати з I класу.

Розвиток лог\чного мислення у молодшому шкјльному        —

передумова людини, бо, як показали та педагог'в, саме цей Bik сприятливий для навчання виконувати      для розвитку творчо\

М В Богданович включив до чинних з математики

P13Hl види задач i пропонуе розв'язувати 1х з учнями на етапах уроку:        час усно\  та

узагальнення знань, хвилин      математики початкових      недостатню увагу розв' язуванню цих задач, тому у    i старших k-naciB виникають     час розв'язування задач з лопчним навантаженням розв'язувати задачу передбача€ знання тих загальних правил,      сприяють  до розв'язання. В широкому p03YMiHHi розв'язування розпочинаеться i3 збирання   Вивчають запитання       згадують або знаходять з певних джерел Ti ознаки i       величин, про     йдеться в задам.

У    BMiHb розв'язувати велике значення мають i      заходи навчального i виховного характеру.     треба opieHTYBaTH на таку настанову: над розв'язуванням      треба думати, ockiJlbkll ПРИЙОМИ знаходження не      ix noTpi6H0 знайти. Тому при умови не   вонтт N0BllHHi

мати час на

Метою даного с сприяння розвитку творчих ,       ix до навчання в старшпх класах,

i на уроках i    час проведення математичннх змагань,

i для                                                                 домагнньо\ роботи

1. МЕТОДИКА РОЗВ'ЯЗУВАННЯ ЗАДАЧ З ЛОПЧНИМ НАВАНТАЖЕННЯМ

Використання задач з       навантаженням в початкових класах зумовлене   особливостями молодших шести, семи P0kiB дитина здатна користуватися схематичними зображеннями  У сво\х вона вже менше залежить вт наочних ознак речей. Мислення учня      якщо перед ним виникають запитання, на

BiH одразу      не може. Саме в таких умовах знаходяться що розв'язують     з лоАчним навантаженням математичними задачами з       навантаженням для молодших       Taki, розв'язування яких потребуе    врахування взаемозв'язкав     даними 1 шуканими величинами; правильно\    кожного окремого компонента    властивостей арифметичних та величин, безпосередньо не Bka3aHi в YMOBi, але випливають з певних причинних чи залежностей. Задачами з   навантаженням можна назвати i розв'язання яких вимагаеться щось    узагальнити тощо.

        Використання задач з                     навантаженням , якщо

А) для роботи над ними 7-10 Хвилин уроку дватри рази на тиждены,

Б) розкривати умови задач  i образно спираючись на

В) учням дати змогу  думками,

висловити pi3Hi                подумати над розв' язанням вдома.

При колективному  засвоення умови i деяких p03MipkYBaHb вчитель пропонуе бажаючим уголос про до розв'язування задачу, , про що в    можна одразу  чого не вистачае для розв'язування тощо. Критично  Taki

3' ясовують едино можливий шлях розв'язання або знаходять    з к\лькох.

Записувати в зошит розв'язування з навантаженням не обов'язково. Але розв' язку мае

проведено так, [1106 BCi учн' класу усвйдомили i процес розвлзання. i oc06J1llBic1b

Пермим       кро ком лопчним

навантаженням с '[х вид1лити групи J]or-iLlHi задач( i [liIJBII[IleH0i трудностт

е для розв'язання яких не вимагаеться виконання арифметичних або (

розкласти на 5 було непарне?).

в яких треба враховувати просторове розмпцення (Хлопчик пройшов BiH повернув назад i пройшов ще 40 м. На       дерева знаходився хлопчик?) при  яких треба враховувати обставину, яка явно не вказана в TekcTi (У токарному цеху виточують з металевих заготовою З       заготовки виходить одна деталь час обробки стружки      у     З них при 6 деталей можна виплавити одну заготовку. деталей вийде i3 36 заготовок?), на визначення BCix можливих BapiaHTiB (У ящику було З червоних i З зелених палички. Хлопчик узяв 4 палички. Якого кольору вони могли бути ?       паличок кожного кольору?) на     та з'ясування причин ix порушення (На рисунку       карась, щука, окунь. i акула. Хто туг зайвий?) можна розв' язати способом випробування (На     i ходили У них всього 6    а     16. було овець 2)

    — висловлення (Чи завжди              Taki твердження:

день коротший  мае 30 березень мае 31 день?) на доведення (У навчаеться 400 Довести, що хоча б 2 з них народилися в один i той самий день;)

 на cnoci6  вилучення (Три

Береза, Верба i Тополя — посадили 3 дерева. березу, вербу i тополю. Жодна з них не посадила дерева, якого

         Яке дерево посадила кожна учениця, якщо      що

Береза посадила не тополю0)

Серед арифметичних задач  можна Taki ВИДИ:

в       розв'язування яких,   треба розглядати у зворотному порядку (На двох

Коли один горобець    з     на другу, то на обох     стало по три на спочатку?) з понятгям «частина» (Коли     пройшов половину шляху i ще 4 км. йому залишилося пройти ще чверть весь шлях.) числовими даними в початкових класах не входять до програмного MiHiMYMY.

Серед типових задач в початкових класах для роботи i3 учнями можна використати Taki: знаходження величин, знаходження числа за сумою i на суму i кратне  двох чисел, на припущення, на 3aMiHY i даних.

Розв'язки типових задач молодших шукають не за  алгоритмами а шляхом розмјрковування, практично-наочного виконання.

Н. ОДИК•Л роьолм ТИНОВИМ“ ЗАДАЧАМИ Рези „лянемо методику роботи над такими задачами

на знаходження  за сумою i

2                                                        3aaatli на знаходження HeBiL!0Ml1x за сумою (чи )  кратним втношенням.

3                                                        '3anaqi на 3aMiHY

4                                                        “3адачА на припущення.

5                                                        на       даних.

Bci    можна розв'язати способом складання       чи системи      у     та сгарших класах, а        менш способом складання      HaBiTb у початкових класах. Але для молодших   такий      розв'язання важкий. бо вони не вивчають i      час розв'язування на одну,       користуються лише зв'язками мгж компонентами i результатами дйћ. Тому вважаю, що розглянути Taki   саме у TpeTix — четвертих класах, використовуючи понжггя «частина» 3aMicTb х, або умови задач за допомогою  Добре, коли    знаходять  у багатьох з наведених    задач шляхом

Це потребу€  швидко оперувати числовими виразами, знаходити ix значення. бувае так, що учень на запитання, як довести, що твоя правильна, пояснити як ти знайшов, не може BiH не встиг глибоко швидко виконав його мозок, Завдання вчителя — допомогги довести чому саме його правильна.

час       учень навчаеться доводити CB0i твердження i глибше    3MiCT задач[ мають способи розв'язання типових задач ,       не входять до обов' язкового програмового MiHiMYMY, i   користуватися для кожного виду задач.

такими  залежить

правильно обрано\ вчителем мегодики роботи над задачами,   до   систематичного використання задач з навантаженням на уроках та позакласних заходах з математики

l. BAAAIII HA引ー、\ ()は木日Ⅲ日トBいいMい、ハ(、Mいロ

3出いーー

2      с о с 1 6 розв•язання

ДАО 4 О 3aMiHHTH на 32-12= 20 (шт )-  качок

3      c n o c i б розв'язання,

гусок на

1)       32+8 = 40

2)       40 2 = 20 (шт ) —качок, З) 20- 8      (шт.) —гусок,

розв'язання задач на уроках та позакласних заняттях показати учням, як самим Тх складати. Продемонструемо на складання задач на знаходження за сумою i

В ч и т е л ь: Вам взяти два числа. що позначають якихось тварин, дерев, тощо.

Н а п р и к л а д: Взяли два числа 9 i 15. Це будуть в YMOBi будуть сума чисел 9 + 15 = 24 i 15 6 , тобто на одне число чи менше, друге. Залишилось скласти умову за обраним сюжетом„ Наприклад.

Задача 1.2.

На    стояло 24 голубих i рожевих Голубих на 6       рожевих,      окремо голубих i рожевих     стояло на такого типу з двома  числами е у М В „Богдановича 3-4 класах. Для проведення математичних змагань у     чи   паралельними класами, для математичних       рекомендують    на знаходження трьох     чисел за ix сумою та     Таких задач у та        для дуже мало. тому

важливо вчителю складати i розв'язувати з «сильними» та учнями». «Слабким» учням буде корисно вислухати пояснення cB0ix Наприклад:

Задача 1.3.

У трьох  була 41 цукерка. Коли перший 7 цукерок, другий 3 цукерки, ато у кожного залишилась однакова  цукерок. цукерок було у кожного хлопчика спочатку9

Роз в 'я з а н ня

Якщо позначити kiJ1bkicTb цукерок , що залишились в кожного хлопчика, одною частиною або  , то спочатку у першого хлопчика була (1 ч. + 7 ) цукерок, у другого — (l ч . + З ) цукерки i в третього — (1 ч +4) цукерки.

I.

41ц

1) 7 +3 +4 = 14 (ц.) — 3 хлопчикуг, 2) 41 — 14 = 27 (ц.) — припадае на 3 ч. З) 27 : З = 9 (ц.) —припадас на 1 ч.

4) 9+7 = 16 (ц.) —було у 1 хлопчика 5) 9+3 = 12 (ц.) — було у 2 хлопчика. 6) 9+4 = 13 (ц.) — було у З хлопчика.

TI e p e B i p k a: 16+ 12+ 13 = 41 (ц.)

В п о B i д ь: 16 цукерок, 12 цукерок , 13 цукерок.

Для навчання      корисно розглянути з ними 7 cnoc06iB розв'язування наведено\ матимуть нагоду caMi знайти       за    час. роботи глибше i cnoc06iB розв'язання

7) 1 6 -3 - I З (ц.) - було У З хлончика,

З с н о c i 6

Цсй спос'б вецЫзнясться в'д 2 способу лиј]1С останнЈми 7) 12 -Ј- 16 — 28 було у I i B 2 хлопчик;в, 8) 4 1 — 28 — 13 (ц.) - було у З хлончика.

4 c n o c i 6 цуксрок, I.T(0 бујш в i З xJ10HtIP1kiB 3 Tioo kiJlbkicT0 цукерок, ;пса була спочатку у 2 хлопчика.

7  на cTiJlbk14 треба зменшити kiJIbkic3A) цукерок, ака була у першого хлопчика•, на    треба зменшити цукерок у З хлопчика

3)           4 А- I— 5 (ц) — наслјльки треба зменшити цукерок, що була спочатку у першого i трегьотх» щоб у BCix  було спочатку цукерок nopiBHY, як у

другого;

4)           41 - 5 - 36 (ц) - noTpi6Ha  цукерок, щоб була у другого хлопчика спочатку•,

5)           36 / З = 12 (ц) — було у другого хлопчика•,

6)           12 + 16(ц) — було у першого хлопчика•,

7)           12 + I = 1 З(ц) — було у трегьошх) хлопчика.

5 c n o c i 6

Цей c[10ci6 четвертого лише 7) 12 + 28(ц) — було у першого i другого хлопчикйз•, 8) 41 - 28— 13 (ц) — було у трегього хлопчика.

6 cnoci6 цукерок, що були у першого та другого  цукерок, яка була у

третього хлопчика,

— треба дати другому хлопчику;

2)          7 —4 = З (ц) — noTpi6H0 забрати у першого хлопчика•,

3)           — на менша була б загальна цукерок спочатку, якби у першого та другого цукерок було  у трегього хлопчика.

4)          41 — 2 = 39 (ц) — було б у трьох хлопчикЈв, якби у BCix цукерок було б nopiBHY, як у третього хлопчика.

5)          39 / 3 = 13 (ц) — було спочатку у третього хлопчика;

6)          13 + З =16 (ц) — було спочатку у першого хлопчика, 7) 13 = 12 (ц) — було спочатку у другого хлопчика.

7 c noci6

BiH шостого способу

7) 13+16= 29 (ц) — було в трегього i першого спочатку; 8) 41 — 29 = 12 (ц) — було в другого хлопчика.

2. ЗАДАЧЈ НА ЗНАХОДЖЕННЯ НЕШДОМИХ ЗА СУМОЮ (РВНИЦЕЮ) КРАТНИМ ВЩНОШЕННЯМ.

Taki с в  lx можна почати вводити з третього класу, послупово ускладнюючи в четвертому  i навички,  час розв'язування задач попереднього виду, будуть 3acTocoBaHi в нових умовах, якщо робота над задачами проводитиметься в при

ДО        iM скороченого запису умови задач, Наприклад:

Зада ча 2.1.

Максимко 3i6paB 2 кошики капусти. У першому кошику капусти у другому,  капусти в кожному кошику, якщо всьогоп 8 кг?

Р оз в я з а н н я

Виконаемо скорочений запис умови зобразивши масу капусти в кошиках з допомогою або позначивши в частинах. У другому кошику — ч., у першому кошику — З ч. капусти

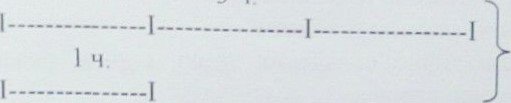 8 кг

1)         3 + I = 4 (ч) — капусти в двох кошиках;

2)         8 / 4 = 2 (кг) — припада€ на I ч. в другому кошику; З) 2 х 3= 6 (кг) — в першому кошику к а: 2+ 6= 8 (кг).

В i д п о в i д ь: 6 кг. капусти в першому кошику, 2 кг — у другому кошику.

Щоб      навчилися    складати звернуги \хню увагу на те, що в    2. I шуканими е два числа, kpaTHi     собою, тобто одне з них в      pa3iB

(менше),                                            сума цих чисел i ix кратне

Наприклад, за I число Bi3bMeM0 16 , за друге число 64, ix сума

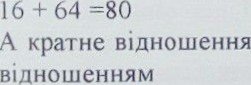 64 16 = 4. А         за сумою 80 i кратним

4: I можна скласти умову               обравши pi3Hi сюжети.

Задача 2.2.

В ящик поклали 80 яблук i груш при чому яблук в 4 рази  груш. окремо яблук i груш в кошику?

         Якщо для складання умови          взяти чисел

64 : 16 = 4 та ix  64 — 16 = 48, то можна скласти задачу

2.3. на знаходження  за ix  i кратним

Задача 2.3.

В ящик поклали i яблука, при чому, яблук в 4 рази  HiA< груш. окремо поклали груш i яблук в ящик, якщо яблук на 48 штук груш ?

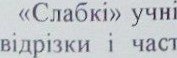
Р о з в 'я з а н н я можуть розв'язати цю задачу, використовуючи i i частини для позначення груш та яблук.

«Сильним» учням достатньо ввести позначення в частинах : ч —     яблук.

Розв' язання складених задач, сприяе розвитку навичок самоконтролю в

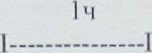Ябл. 1---------------1-----------------1---------------48 шт. гр

= 3 (ч.) — на  яблук, це складае 48 шт.;

2)           48 : 3 = 16 (шт.) — припадае на I ч. , груш,

3)           16 х 4 = 64 (шт.) —  Яблук ; або З) 16 + 48 = 64

(шт.. )

Яблук — 64, груш — 16, що складання за обраними числами.

Задача 2.4

Для      заготували крупи. В використали 100 кг kpyniB, а за   i лютий разом — в 4 рази       за грудень. цього залишилось 80 кг kpyniB. kpyniB було заготовлено?

Р о з в ' яз а н н я.

Складаемо вираз та обчислюемо його.

100+ 100 х 4 + 80 = 580 ( кг)

Знайшли суму — 580 кг, а кратне — в 4 рази — було в YMOBi. Тепер можемо скласти до обернену на знаходження за сумою i кратним (2.5)

Задача 2.5.

Для заготували 58() кг крупйз, За грудень використали в 4 рази менте kpyniB, за ciqeHb i лютий разом. цього залишилось 80 кг kpyniB. CkiJ1bkH  використали за i за лютий разом?

Р о з в ' я з а н н я

Позначаемо масу kpyniB використану в грудн' - i в лютому разом — 4 ч.

1)          4 + I = 5 ( ч.) - всього використали

2)          580 — 80 500 (кг) —припада€ на 5 ч

3)          500 5 = (кг) припадае на 1 ч спльки kpyniB використали в грудн(

4)          100 х 4 = 400 (кг) — припадае на 4 ч.; використали в i лютому разом.

400 кг.

Одержали Taki числа були в YMOBi прямо\ тому обернена задача розв'язана правильно.

викликае в розв'язання та складання задач, в яких шуканими е 3 числа, кратним ыдношенням, а B1!10Mi за умовою та загальна сума чи числами як у 2.5.

Залежно особливостей класу вчитель може спочатку пояснити в евристичној розв'язання задач даного виду, а навчити ix складати, або спочатку скласти разом з ними задачу даного виду, як обернену до виконувати яку входить в програмовий MiHiMYM знань а noTiM навчити 1х розв'язувати. Наприклад.

Задача 26

840  працюють у трьох цехах заводу. В першому цеху працюе в 4 рази людей, в 2, а в З цеху — менше, у 1. p06iTH14kiB працюе в кожному цеху?

Р о з в'я з ан н я

          Вчитель проводить            з учнями:

 В якому цеху найменша  ?( у

 у 2 цеху I ч . або коротким

позначити kiJ1bkicTl) p06iTH\1kiB исху9 Чому ч. в 4 рази бшьше, у 2 цеху).

; Чи можна визначити, CkiJ1bkV1 частин складае: ктльюсть p06iTHHkiB 3 цеху? Чому9 (2 ч „ менше , у цеху) довжини будуть шо позначають I i 3 , з 2 цехом?  Яким буде запис умови задан'?

840 р

III

 Що треба знати, щоб розв' язати задачу? припадас на ч V)

               Яким буде план розв'язання             7

 Про що спочатку, про що потјм ?

1)             + 2 + 4= 7(ч.) — всього складають 840

2)             840 7 = 120 ( р. ) припадае на ч . пращоють в 2 цеху;

З) 120 х 2 = 240 (р ) —працюють у З цеху; 4) 120 х 4 = 480 (р.) — працюють у цеху

р к а:

120 + 240 + 480 = 840 (р.)

В i д п о в i д ь : 480  120  , 240

Щоб скласти умову  можна взяти З числа — частини, i ввести таке значення для першо1 частини, яке можливе за обраним до сюжетом. треба знайти значення невщомих чисел та тх суму чи якусь i3 Наприклад ,

ч; 3 ч; 5 ч — це 3 у частинах. На одну частину, припустимо, припадае 50 штук першого виду 50 другого 50 х 3 = 150 i третього виду

50х 5 = 250

     50 = 250 = 250 = 450 —              усього

За числовими даними ч. , 3 ч i 5 ч, , 450 Складемо задачу 2.7

З адача 2.7.

У      продаються 450 3-х другого виду ,    першого виду, а     3 виду — у 5 pa3iB   першого виду.    у MakBl414i кожного виду окремо?

З. З АДА Ч 1 НА ЗАМЈНУ.

Задач такого виду дуже мало в  З — 4

Учням найважче      нову форму запису умови      та поняття       на  така 3aMiHa , як нею скористатися для розв'язання задач[ Тому спочатку краще ознайомити  з такими задачами , в яких i запис умови i розв'язання можуть бути      до задач на знаходження        за сумою i кратним розв'язання задач    способом учитель знайомить 3i способом Наприклад:

З адач а 3.1.

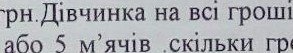Лялька та м'ячик коштують 12 . що в були . могла купити ляльку або 5 грошей було в

Роз в'язанн я

Позначмо м'яча ч. або маленьким , а ляльки -5 ч. , або , який у 5 pa3iB довший , перший.

л---------I---------I---------I

12 грн.

м

1)                  + 5 = 6 ( ч.) — становлять 12 грн.

2)                  12 : 6=2 (грн,.) — припадае на I ч „ коштус м'яч /

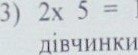= 10 (грн.) — коштуе лялька. або 10 грн. було у

Цю задачу можна розв'язати   способом, який називаеться способом  при цьому частини вводити не будемо.

Скорочений запис умови  може буги такий Л. (М. - 12 грн. (1) л(2)

      Ск(льки грошей було в                   ?

3aMiHHM0       ляльки   5     у  (1). тобто   1 м'яча — це як 1 ч. в попередньому розв'язання

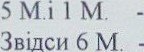12 грн - 12 грн.

1)   12: 6 = 2 (грн) — коштуе м'яч;

2)   2 х 5 = 10 (грн.) — було у  ляльки.

Пе p e B i p к а: 10+ 2 = 12 грн — коштують лялька та м'ячик.

на 3aMiHY можна розв'язувати з учнями 4 класу на позакласних заходах чи       року        час проведення математичних змагань У таких задач нема. Зразок розвязання       з таких задач. Задача 3.2.

важать   ciM легший за на 40 кг. Яка

Розв'язання:

        Умову                                         можна коротко записати у двох

2м.к. -7 м,ц. (1)

1 м.ц. +40 кг - lM.k.(2)

1 MilllOk з картонлею на MiJ]0k з пибулею                                                                                                                 кг у

Так як

I) \ 2 = 80 (кг) , то будемо мати

2 м ц + 80 кг - 7 м ц, (3)

    Зменшимо     i праву частини у  (3) на 2 м ц.

5м ц - 80 кг,

2) 80 5 = 16 (кг) -маса м шка U e p e B i p k a.

1)      16 + 40 = 56 (кг) — масса   картопл(

2)      56 x 2 = 1 12 (кг) — масса двох   картоплй

3)      16 х 7 = 112 (кг) — масса семи 1 12 = 1 12  маса  16 кг

4.               на припущення.

 час розв'язування задач такого виду учням 3-4 важко зробити припущення      такого закону. Якщо числа в YMOBi задачг намагаються розв'язати задачу способом До такого способу корисно заохочувати особливо в 3 проводячи, наприклад, конкурс на кращого обчислювача. Але noTpi6H0 продемонструвати, що таким способом не завжди можна скористатися, а     припущення допомагае розв язати задачу за будь-яких числових даних. Розв'язання задач на припущення викликае в  також тому, що вона включае, як складову частину, розв'язання задач на знаходження за двома  а це досить  за програмою для 4 класу.

Задача 4. I

В 20()      Школа замовила для них 22 намети. В      е намети на 10 i на 6 для школи HaMeTiB кожного виду9

Р о з в' я з а н н я

Припустимо. що BCi намети на 6 Micub_

1)                       б С 22 = 132  б;

2)                       200- 132 = 68 (м.) — не вистачало б,

3)                       - 6 = 4 (м.) — на Micub в 1 намет\ на

      М'СЦЬ,             В 1 HaMeTi на 6

4)                       68 '     17    на 10

5)                       22- 17 = 5 (н.) - на 6 м'сць noTpi6H0.

170+30=200

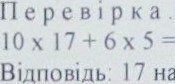17 HaMeriB на 10 MiCL!b; 5 HaMeTiB на 6

Задача 4.2 купив на ринку 7 кг Яблук та моркви. Яблука коштували по 2 грн. за один кг, а морква по 60 к. за кг.

окремо Яблук та моркви купив  , якщо витратив на них кл.)

Розв яз анн я

          Припустимо, що                 купив 7 кг Яблук

1)                      2 х 7= 14(грн.) - було б витрачено ,

2)                      14 грн. - 11 грн. 20 к. = 2 грн.80 к - на  було б витрачено грошей;

3)                      2 грн - 60 к. = 1 грн. 40 к — на Яблук        за ну моркви ,

4)                      2 грн.8О к. : грн.4О к. = 280 к.: 140 к. = 2 ( кг) - моркви

купив

5)                      7 -2 = 5 (кг) - Яблук купив

1)  2х 5 -¯ 10 ( грн) - коштували яблука,

2)  60 х 2 = 120 = грн.2О к. - коштувала морква; З) l() грн. + грн.20 к. = ]1грн.2О к.- витратив

 5 кг Яблук , 2 кг моркви.

Найлегше скласти задачу на припущення, як обернену до npocroi задач1 на знаходження суми двох  Наприклад, Задача 4 3

Купили 20 блокнотЈв по 4 грн. i 50  по 2 грн. CkiJlbk[l грошей заплатили за BCi блокноти ?

Розв 'язання математичним виразом 4 х 20 + 2 х 180 грн.

Складемо обернену задачу 4.4. на припущення.

Задача 4.4

За 70  заплатили 180 грн. Серед них е блокноти по 4 грн. i по 2 грн. Склльки  кожного виду купили?

Роз в ' я з а н н я.

Припустимо, що купили 70  по 2 грн.

1)   2 х 7() = 140 грн. - заплатили б за блокноти ,

2)   180 - 140 40 грн. - на  коштували блокноти тому , що серед них були блокноти по 4 грн.

3)   4 - 2 = 2 грн. - рызниця в

4)   40 : 2 = 20 (б.) - по 4 грн. купили , 5) 70 - 20 = 50 (б) -по 2 грн.купили.

: 20  по 4 грн., 50  по 2 грн.

5. ЗАДАЧ! НА ЗРТВНЮВАННЯ ДАНИХ.

на  даних у старших класах розв язуються складанням системи з двох  YHHi початкових будуть краще  до навчання в старших класах, якщо  що piBHicTb залишаеться правильною, коли    ii частини помножать чи на одне й те саме число, або коли    другу Саме таких властивостей     сприяе розв язання задач на  даних. Наприклад.

Задача 5.1.

Три альбоми i чотири коробки коштують 18 грн„ П ять таких  i коробки коштують 16 грн, коштуе одна коробка

Р о з в ' я з а н н я

Запишемо скорочену умову задагп

(1)    3 альб. i 4 кор.- 18 груз, /

(2)    5 альб. i 2 кор.- 16 грн. [2

Помножимо (2) на 2 шоб 3piBH51TH юльюсть коробок в (1) i (2).

3 альб i 4 кор - 18 альб i 4 кор.- 32 грн.(З)

(1) i (З), [3apTicTb у

(3) 6iJ1bwa,            в (1) тому , що                 aJlb60MiB.

1)     10 - 3 = 7 (альб.)-на ;

2) 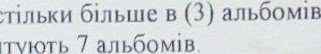    32 - 18 = 14 грн„-кошлують 7

3)     14 7 = 2 (грн.) -       альбому ,

4)     2 х З = 6 (грн.) - кош•тують З альбоми ;

5)     18 - 6 = 12 (грн.) - коштують 4 коробки 6) 12 : 4 = З (грн) - коштуе коробка

2 х 5 + 3 х 2 = 16 грн.

: З грн. коштуе коробка

111. СИСТЕМА ЗАДАЧ З ЛОПЧНИМ НАВАНТАЖЕННЯМ.

 на знаходження                         за сумою i

1.        У двох качок 24 каченяти. У на 4 каченят у качки. (14 к., lOk.)

2.        назбирали два кошики яблук. У першому кошику на 6 Яблук менше, у  Яблук у кожному кошику, якщо всього 3i6paH0 30 Яблук ? ( 12 яблл 18 ябл )

З. Спортивний костюм коштуе 36 грн. коштують штани, якщо куртка на 24 грн дорожча ? (106 грн.)

4. Хлопчик i  виготовили 15 кружечкйз.

виготовив кожен з них, якщо що хлопчик виготовив на 5 ? (10 к; 5 к.)

госпо.'ШНЬ 67 кг яблук. У - на 5 кг яблук у nepruoi. У TpeTb0i - на 12 кг яблук б'льше, у кг яблук у  ( 20 кг ; 15 кг 32 кг)

ЗАДАЧ1 НА ЗНАХОДЖЕННЯ НЕШДОМИХ ЗА СУМОЮ (РВНИЦЕЮ) I КРАТНИМ ШДНОШЕННЯМ.

1. Хлопчик за 2        прочитав книжку, в 147 cTopiH0k. Першого дня BiH cTopiH0k, другого дня.       cTopiH0k прочитав хлопчик кожного дня окремо.(98 с „ 49 с,)

2 i Микола купили однакових на 6 грн. Причому витратила на них у 5 pa3iB грошей , Микола. CkiJlbk14 заплатили за зошити i Микола.? (5 грн.1 грн).

3.Син з батьком збирали л ikapcbki рослини. Син 3i6paB ix на 10 кг менше, батько. рослин 3i6paB батько, якщо BiH збирав ix у 3 рази син ? (15 кг.)

4.У три гуртки записали 90 перший гурток а у другий -   у записалося у кожний гурток? ( 45 уч.; 30 уч,; 15

5.Дерева садили три бригади       в 4 рази        - в 5 pa3iB менше,        у     якщо всього 150 oci6 ? (60 р.} 15 р.;

ЗАДАЧ] НА ЗАМШУ.

1.          Висота 6 6epi30k разом така, як у З тополь разом . Одна тополя виша, бер[зка на 4 мегри. Яка висота (8 м.)

2.          Фарби i пензлик коштують 30 грн. студент на сво\ купити фарби або 5  грошей мав грн.)

3.          з борошном важать ж, 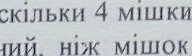з картоплею.       з картоплею на 15 кг важчий,     з борошном. Яка маса       з картоплею ? (45 кг)

4.          BapTicTb двох BapTocTi 8 дешевша,    грн.5О к. Яка       ? (2 грн.; 50 к.)

5.          На пошиття двох  тканини, як на 6 сорочок. На пошиття плаття i сорочки витрачаеться 8 м тканини. MeTPiB тканини noTpi6H0 на 2 плаття ? (12 м)

ЗАДАЧ НА ПРИПУЩЕННЯ.

томатного соку законсервували у 40 банках використали

31 банка по I

2.     У Micbk0MY парку гуляють  3i собаками .За минулий день у парку побувало 140 oci6 i собак . Усього - 440 та лап. собак побувало в парку минулого дня ? (80 собак)

3.     У    30   i 800

30       а в по 25 у кожному i по 25 по 25

салка кт.лили 50 irparuok. зап:ив кошт.та.ли 230 грн За машинки Платили по 4 трн . за зай:нв - по S грн Ск\льки КУПИЛИ машинок i ск'льки зайи•вт (20

5 H0Tpi6H0 перевезти на 22 човнах 64 особи С човни на 2-х та

4-х oci6 кожного виду о ( 10 на 4 особи , 1 2   -на 2 особи)

ЗАДАЧ] ЗЛОПЧНИМ НАВАНТАЖЕННЯМ ГПДВИЩЕНО1 СКЛАДНОСТ1

I 64 роки, його синов i 40 P0kiB, а 0HYk0Bi 12. Через P0kiB Bik  CYMi P0kiB сина та онука?

(12 P0kiB).

2. У двох - 140 кг борошна. Якщо з першого пересипати у другий 10 кг борошна, то в обох стане борошна стане nopiBHY. борошна в кожному (80 кг, 60 кг)

З.У двох разом ll Якби в з них стало на 5 то вона мала б у три рази друга у (7 ол., 4 ол.).

4. 53 роки, а 0HYk0Bi - З Через  P0kiB буде в 6 pa3iB старший за онука ? (через 7 P0kiB).

пшеницею 160 га, а кукурудзою -140 га З га одержали кукурудзи на т Загальний 36ip зернових склав 740 т. (320 т).

IV. АНАЛВ ТА РОЗВ'ЯЗУВАННЯ ЗАДАЧ З ЛОПЧНИМ НАВАНТАЖЕННЯМ У КЛАСТ

Математика: Богданович М.В К: 0cBiTa. 2007

N25 стор . 26

 Що таке ширма 9

('к'льки слон'в -гримають гнирму ? (2) l_llo запилусться в задачР (Ск\льки слон'в за ширмою0) CkiJ1bkll 'јрсба додатн до 2 одержати (5 9 (4) 2 +4 =6 (с)

В'дпов'дьј за изирм0)0 4 слонн.

Тиме мова в було частинок шоколаду ? мишки з     ? ; CkiJ1bkh заЛИШИЛОСЯ ?

г Якою розв язусться задача ?

9- 6 = 3 (ч)

: з З частини шоколаду.

Ne4 стор, 74

Хлопчик— 5 ок.

- ? на 2 ок менше 9 г 0kYHiB п'ймав хлопчик ? (5)

            ;                                       0kYHiB ? (на 2 0kYHi менше)

                ; Якою             можна

5-2= 3 (ок.) г -Чи можна тепер  0kYHiB вони разом ?

5+ 3 =8 (ок.)

: разом  8 0kYHiB

6 стор 78

Хто зображений на малюнку ?

                 Хто сидить         на            Tepe3iB ? (кенгуру).

Хто сидить справа ? ( лисиця) kpiM , що ще сто'ть на Tepe3iB ? ( масою 2 кг)

                 Про що запитусгься в               ?

 Чому  маса кенгуру 9 ( Maci лисеняти + 4 кг )

        Отже , кенгуру на 4 кг важчий,          лисеня

 5 стор 82

                                                        4                          6

- - -------I----------I----------I

                             P0kiB                    ? ( 6)

                                  P0kiB BiH старший в1д         ? (2)

> Що питаеться в

Поглянь на числовий                                                      на

Чому повернена на ? Адже Миколка старший на 2 роки Якщо Миколка на 2 роки старший, То Оля на 2 роки молодша. Отже, що знайти P0kiB

Треба 6 зменшити на 2 ).

5-2=4 ( р.)

4 роки

N9 З сгор. 90

        Кого ми бачимо на              Tepe3iB?

         Хто сидить               хто сидить справа? Що питаеться в

 Що можемо сказати про масу собачки? (Його маса Maci двох      ?)

М 5 стор. 91

Було 5                                         Стало 9

Подарували -

           Що             в             ?(перший доданок , сума )

Що n0H)i6H0 знайти '? ( другий доданок доданок ?

 7 стор . 110 ckiJ1bkWT яець у  ( 10)  Скальки яець зварили ?

яець залишилося ?

        Якою           ми  ?

Було — 10 яець Зварили — 4

Залишилося - ?

10—4 = 6 ( яець) залишилося 6 яець.

N26 стор , 1 1

— 10 р; на 4 роки молодший CecTPi -?

            Як ви вважаете                    P0kiB cecTPi ? (14)

 Як ви д(зналися ? ( 10+4 = 14 )

 А чому ви додавали, адже там сказано, що на 4 роки молодший? (Це Сашко на 4 роки молодший сестри, значить сестра на 4 роки старша )

14 P0kiB.

N2 6 стор. 113  козенят живе в будиночку ? ( 7) козенят на прогулянку ? ( З) ск1льки козенят залишилося ?

4 козенят.

N2 6 стор 14 кульок було в TaHi ? (8 круглих i 6 довгих )

 Хто забрав кульки '? ( песик )

лова кульки, 60 в Hiii

паличок гусей було спочатку Чи можемо ми показати на ставок. (Hi, це не

          А чи можемо показати                 залишилося

         6 паличок) Що означають палички,                                    залишилися

HepyxoMi (Гуси,     на ставок     ix (8) Як про це можна    (14 — 6 )

8 гусей.

N2 6 стор 122

Качок

Гусок

[ндичок

Що треба зробити , щоб  два числа ? (

менше )

Чого було ? ( ) Чого було менше 9 (гусок )

        ; Яку          треба виконати ?

= 4 ( тнд.)

     :                було на 4

N2 6 стор 124

            СкЈльки книжок на               '? ( 7 )

          ; А на               ? (4)

       ;                  всього книжок '? ( 1 1)

: l l книжок книжок на [10J11Fll4i? (7)

    ; А на     ? ( 4 )

        ; На                             книжок на

7 -4 = 3 (к.)

: на З книжки

5 стор 125

-Яку парту ми називаемо ;       таких парт ?

, нВк на CTOJ1i '?

?

запишемо приклад, у якому порахуемо BCix  сядуляэ за 4 парти

     ЛА), чи можемо ми посадити за них 7 yqHiB ? 10           9

слор 130

 Куди бабуся i Микита ? [Цо купила бабуся ?

 0BOHi може нести Микита ?

 може нести цибулю i моркву, або капусту.

IV. АНАЛIЗ ТА РОЗВ'ЯЗУВАННЯ ЗАДАЧ З ЛОПЧНИМ НАВАНТАЖЕННЯМ У 2 КЛАС!

Математика  Богданович М.В К: 0cBiTa. 2005.

ЈУ2 14 стор 5

- 6

              - на 4

- на 2 менше

Що сказано про каштани ? (що ix посадили на 4

                     Якщо на 4  то яку                       треба виконати?

(додавання)

 Що сказано про ? ( що тх на 2 менше ,

     Яку        треба виконати ?

1)    6 + 4 = 10 (д.) — посадили

2)    6 - 2 = 4 (д.) — посадили посадили 10

Хе 23 стор 6 дерева поливав Олег?

; Ha3BiTb  дерсва ( яблунп, СкАльки полив яблунь? (4) полив груш? (3) всього фруктових дерев'?

4 + 3 =7 (д)

7 фруктових дерев,

 39 стор. 9

> Кого ми бачимо на терезах ?

           Хто            ? (песик , гиря [кг)

> Що справа ? ( гиря 2 кг , 5 кг)

        > CkiJ1bk13 разом кг справа ? (5 +       7 кг)

         > Що означае гиря            ( що один кг треба забрати )

          > То як ми                     , яка маса песика? ( 7 — I = 6 кг)

1)              5     7 кг — маса гир

2)              7 — 1 = 6 кг — маса песика  маса песика 6 кг

 1 В стор .23

          > Що сказано про масу              ? ( 8 кг)

; Яка маса енота ? (5 кг)

> Як д1знатися масу лисеняти ? ( 8 — 5 = З кг )

Знаючи масу лисеняти , як nopiBH51T11 ix масу ? ( менше )

1) 8 — 5 = 3 (кг)

2) 5 - 3 = 2 (кг)

: маса снота маси лисеняти на 2 кг.

 128 стор. 25

 CkiJ1bk[t  В 1вася ?

; Що зробив хлопчик ? ( p03pi3aB на 4 трикутники ) Отже, з одного чотирикутника, ckiJ1bkIJ вийде ? (4)

А з двох ? ( 8)

4 +4 = 8 ( т.)

 8 трикутник(в.

16 1 стор.З2

Коли нам юдомо суму i хоч один i3 як знайти доданок? (треба   суми     доданок )

19- 12 = 7

N9206 стор. 42

Ha3BiTb числа другого десятка (1 1, 12, 13, 14, 15, 16, 17, 18, 19

20)

 А тепер cka)kiTb, у якого числа другого десятка одиниць на 5  його ) : число 16.

 227 стор 46

 — 12 манд. — взяли 5 манд.

2- l5 манд.- взяли 7 манд.

 Як  мандарин стало на

12 -5 = 7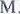

На

15 - 7 = 8 (м)

             На  залишилося              ?

8 - 7= 1  залишилося на мандарину

337 стор 64 деталей виготовляе за одну годину ( 30 д)

CkiJ3bkl! став lAicj1$l вдосконалення ? ( на lO б\льше, тобто 30 + 40 д) знагочи тепер CkiJ1bkll BiH виготовляе за одну годину  як д\знатися ckiJ1bkll за дю годинИ

40 + 40 — 80 (д) за 2 години виготовнть 80 деталей N2436 стор 78

Зобразимо схематично.

24 М

       >                 всього MeTPiB шовку в суво( ?(24)

        > Як                                                 протягом 2         ?

6 + 6 = 12 (м)

> коли ми знаемо       було i   як заЛИШИЛОСЯ ?

l) 6 + 6 = 12 (м)

2) 24 - 12 = 12 (м) залишилося 12 м. тканини.

 474 стор,84

>  каталися на санчатах ? (27)

> А на лижах ? (на 12 менше)

>

>    (6) > Як        ?

15 - 6= 9 (х.)

N2 558 стор.96

Запишемо скорочений запис

п                    - 36

                     - на 12 менше

                  - на 20 менше

       ;             можна  CkiJJbk[l                     треба пофарбувати9

                     36 - Е = 24 (с) Як можна можна пофарбувати ?

2)    24 - 20= 4 ( п.)

          А тепер назвемо                          парт - 36,— 24

 Яку     треба виконати, щоб  разом всього треба пофарбувати?

3)    36 + 24 + 4=64 9м) полЫбно разом пофарбувати 64 парти.

М2 580 стор.99 води у   (80л) стало, коли долили 20 л? (80 + 20) у 2      ? (70 л) взяли води з друго\ бочки ? (ЗОл)

? (70 - 30 = 40 л)

     I бочка                80 +           100 л

     2 бочка                70 - зо = 40 л

М2 598 стор. 103

Хто старший? (брат )

          На              BiH старщиЙ      сестри?

 Як про це д{знаемось? ( 12 - 9=3 р.)

А тепер, коли сестра мае 9 P0kiB а брат 12 р.

12 + l + l + l = 15p. 6paT0Bi буде 15 P0kiB.

V. АНАЛВ ТА РОЗВ'ЯЗУВАННЯ ЗАДАЧ ЗЛОПЧНИМ НАВАНТАЖЕННЯМ У З КЛАСТ

Математика:  Богданович М.В. К.: 0cBiTa .2004.

-М2 19 стор.б хл

                      -7 рибин

15 рибин

- ? рибин

       Чи можемо зразу               на запитання

        Чому ? ( Ми не знасмо                                           рибин )

Знаючи суму i перший доданок, як знайти другий доданок

 94 стор 17

       Що в YMOBi       9 ( всього качок на 2 ставках )

 Що говориться про перший ставок ?

                                    Було                    9

            1 ставок           Плавало -           7

                                    Залишилося       25

 Якою I!i€k) качок в першому ставку ?

25 + 7 = 32 (к. ) —у першому ставку

 Чи можемо ми тепер  качок на 2 ставку

?(Можна)

56 — 32 = 24 (К.)- плавало у 2 ставку  на 2 ставку плавало 24 качки.

N2298 стор 47

Що ми можемо сказати про     банки ? Якщо розлити 18     в банки ,      буде банок9 (18 : 2 = 9)

Яку  розлили в  банки ? (таку саму тобто 18)

Як ми запишемо це виразом ? (18 : З = 6 банок) Ск1льки вийшло банок з соком (9 + 6 = 15 банок) 18        (6.) i3 соком вийшло 15 банок.

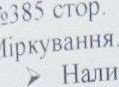Наливаемо в зај1ИШИТЬСЯ т{льки п ять

Ne384 стор. 58

Тарас            

Д 2 трикутники

Юрко              О  у 8 pa3iB

1) 8 х 2 +8 = 24 — 2) 2+ 2 х 8 18 3) 24-18 = 6

N2422 стор.63

6paTOBi  у TaHi i брата можна зобразити так

25-х

У TaHi

У брата

Разом у них 25 але у TaHi на 9 6iJlb[11e. Що буде, коли ми заберемо цих 9 гор\хнзо (У TaHi i брата стане ropixiB [10piBHY). Правильно, обидва стануть довжини. Чи можна vopixiB залишиться в обох разом, коли ми заберемо 9 (разом було 2.5 topi.xiB, якщо забрати 9, залишиться 16) Тепер масмо у двох nopiBHY, а разом 16 Про можна тепер (по у кожного 16 2 = Насправ:м, це у брата стало 8 а TaHi ще лэеба повернути тих 9 ми забрали. То v-opixiB Hacnpats:li змишилося у TaHi ? (8 +9= 17)

Отож. коли Таня передала частину ropi.xiB 6paT0Bi, у нього стало 8. а в неч -

Псреюрка

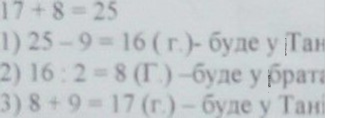i брали nopiBHY

В\.аповпь Твни братом мае 8 mpi\iB

у.4 стог 04

                                       Зд„лишп.лося                        мл:кьли

спочатку

( l ч + 3)

слор 67

План г CkiJ1bk[l всього CTOPiH у трикутника i шестикутника? г Яка довжина одно• сторони? 1) 3 +6=9 ( СТ, Э— ВСЬОГО CTOPiH

2) 54 ' 6 (см) — довжина сторони довжина одној сторони 6 caHT11MvrpiB. N2523 стор 79

чи менше, ?

1)

2) 8 2 —4 (ДОР.)

З) 8 + 4 — 12 (люд.)

12 людей розчищали

N2 561 стор.85

                  Ср        700 г

На ?

 000 г           м.           решта

Знаючи масу металевого зливку i масу  як знайти решту

ООО 700 ЗОО (г)- маса

Щоб        чого    зробити? в{дняти менше).

700 - зоо = 400 (г) на 400 грам NQ650 стор 99

План.

;                                            було ящикйз привезли в другий ki0Ck ?

1)         72 : 8 = 9 ( ящ.) було

2)         9       5 ( ящ.) — до 2 кбоску

5 ящик;в  ДО 2 ki0CkY.

 660 стор. lO() план

CkiJlbk[l коштують цукерки по 9 грн, за кг? Ск\льки коштують цукерки по 6 грн. за кг9 Скћльки всього кг цукерок ?

              Яка        BCix цукерок ?

Ск1льки коштуе кг

1) 9 х 2 = 18 (грн )

2) 6х4= 24 (грн.)

(грн.)

5) 42 6 = 7 (грн.Э

7 грн. коштус I кг cyrv1i111i цукерок.

три  тобто у  е       сестри i ж 6paTiB — 2 брати. Маемо, що у ciM два брати i три сестри, тобто 5

5 у ciM i. N2 776 стор.

1)         63 • 7 = 9 (грн..) — коштуе м тканини

2)         4 х 9 = 36 ( грн..)— CYkHi З) З х 9 = 27 (грн..) — 2 CYkHi тканина для першо\ CYkHi коштувала 36 грн., а для — 27 грн. N2 837 стор. 124 к-----------1------------1------------1

Т----------1-----------1-------------

60 коп.

кг купила господиня кавуна ?(5 —З )

коштуе I кг     ,      заплатила на 2 кг).Знаючи масу кавуна i      I кг коштуе кавун9 ( 5 х 30 ) 1) 5 купила господарка 2) 60 2 =30 ( к.) — коштуе 1 кг.

3)         5 х 30 = 150 (к.) — коштуе кавун

: кавун коштуе 1 грн. 50 к.

N2863 стор.П7

План

> Сюльки Твась прочитав за 5

> Маринка прочитала за 5 ? > всього прочитала Маринка ?

l) 11x 5 = 55 (стор.)-прочитав Твась за 5 2) 7 х 5 = 35 (стор.) — Маринка прочитала за 5

3) 35 + 18 — 53 (стор.) —всього прочитала Маринка

55> 53 , тобто Твась прочитав Маринка

: [вась наздожене Маринку за 5

N9891 стор.1ЗО

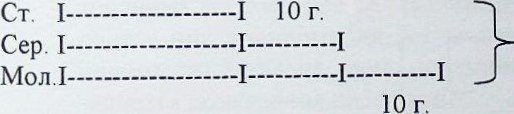      90 г.

Що видно на малюнку? (Якщо забрати 30 «зайвих       то в ycix стане взяла c06i найстарша, а разом - 9() — 30=60 (г)).        можна знайти, що старша взяла c06i (60 ' З = 20 (г); середня — 20 + 10 = 30 (г); наймолодша — 30 + = 40  

Перевђэка: 20 + ЗО + 40 = 90 (г)  найстарша взяла 20 середня 30 а наймолодша - 40

N2961 стор 139

> Що купити за 4 грн. хлопчик? (Лхтарик 3 батарейкою), Отже, чому  BapTicTb

чотирьох батарейок). То за 4 грн. BiH може купити 5 батарейок? (так)

        ; Як                                    коштуе одна батарейка?

           (4грн :        400 к : 5=80 к.)

За умовою купити батарейок хлопчик? (4) як грошей було у хлопчика9

; ( 80 320 (к.) - з грн, 20 к) у хлопчика було З грн. 20 к.

N2978 стор

Що таке квартал? (Квартал — четверта частина року - З  включають 1, 2, З, 4 квартали?

План - 726.

Здавали: 18 х 3 = 54 (б) за три квартали,

 за pik4

74 — 72 = 2 (б) перевиконали план на 2 будинки.

N2987 стор 143

— 40 кг.

Вода 1/8

1)        40 . 8 = 5 ( кг) - маса води, яку бере

2)        40 + 5 = 45(кг) — буде маса через деякий час маса буде 45 кг.

 1006 стор 145 якщо ciTkII цибулин у 2 рази менше, у то що можна сказати про цибулин у

1)          6х2 = 12 (ц) —у

2)          6 + 12 = 18 (ц) — всього  всього 18 цибулин.

АН.АЛВ ТА РОЗВ'ЖУВАННЯ ЗАДАЧ ЗЛОПЧНИМ НАВАНТАЖЕННЯМ У 4 КЛАС1

Математика.  Богданович М.В. К: 0cBiTa.2004

N224 стор 6

           Що можна сказати про будинки,      стоять на одному

                         (BCi номери цих                    або     або

; Давайте спробуемо визначити вони чи знаючи, що сума цих трьох H0MepiB       54.

Р Нехай Bi3bMeM0 3      числа 5+7+9=21 i 3   числа 2+4+6=12

 Яка сума чисел при  непарних чисел? (завжди непарна)

         А при                    парних чисел? (парна)

Давайте спробуемо                              3 числа так, щоб ix сума

54 (16, 18,20)

А чи не можемо знайти

 H0MepiB? Спробуйте 54:3. бачите, виЙшло середне число, Це не випадково. Чому? (бо воно на 2 першого i на 2 менше трегього) якби BCi три числа  18 , ix сума становила б 54. а якщо одне з них зменшити на 2 i додати до  то загальна сума не То як можна записати розв'язання

1)           54 3 = 18 (н)

2)           18 - 2 = 16(н)

 16, 18, 20.

cyxapiB 15 особ. На один тиждень?

cyxapiB на одну особу на тиждень

cyxapiB на один тиждень З кг.

N,'84 стор. l 3

План

Яка маса одного ящика?

2                 Яка маса двох ящикйз9

3                 Яка маса трьох ящикйз9

1)          405=8(кг) — маса одного ядика

2)          — маса другого ящика

3)          8x3= 24(кг) - маса трегього ящика

Ne96 стор. 14

> Як називаються

> Що

> Що не

 Як знайти

 Отже, як записати розв' язання задам.

347 - 129=218 (гр.) у саду росло 218 груш.

стор 15

 Яка довжина смужки? (490 см)

 Як  смужку? (6 см, 8 см,)

> Яка повинна бути ix  (однакова)  Якщо однакова, то що H0Tpi6H0 нам спочатку (довжину 2 смужок).

 Що за цими даними можемо  смужок)

1)        6+8=14 (см) — довжина двох смужок

2)        490 14 - 35(см) — кожного розм'ру

В! лном;ть отрнмаемо 35 смужок кожното розмбру.

менше за

юфажи друге повинна бути у чотирн

I6k4) двох чкел9

II. Повторення i  вивченого Mawepia."Y.

Математичний диктант.

Вчитечь. Даегься вам аж три хвилинки Для розумово\ розминки.

В халепу, щоб не потрапляти,

                        Таблицю         вам добре знати.

21 2 З Усний рахунок.

Два 3Mii великих Михайлику сняться

                  По ciM в них           а всього 14

I кожна зубаста кричить та волае

- Михайлик таблицю не вчить i не знае.

За те Михася годиться .

Бо ж сором який . BiH не знае Михайлик кричить та руками махае - Я знаю таблицю, я знаю. На п ять HaBiTb можу усю Ось 9 на 5 - буде нам 45!

А знав всю ще TOPik у BiBTopokЖ 8 помножить на 5 - буде 40! Ще 24 . от BiCTb коли перемножить 4 на 6 !

                             Не може згадати                      BiH .

Що 7 взяти Немае      у

АЗ на 4 - то буде 12.

-   Коли ще 12 ?- кричить голова, - 12? Як 6 перемножить на 2.

-   То згадуй швиденько i нам говори,

15-це 5 перемножить на З

В не  17.

3 рази по 6 , ясно BCiM -18

А ще , звичайно , бува.

Коли ми помножимо 9 на 2

56

 А що означатиме ця (Ми взнаемо kIJ]bkicTb дјтей у 2  вона не змАнювалася). Коли будемо мати у 2 обчислити ?      бујш у

1)        68 — 4 = 64 (учн,) було б у 2 класах якби у 1 було  ж  у 2 kJIaci

2)        64 6 2 = 32 (учн.)—у 2 uaci З) 32 + 4 = 36 (учн.)— у I

           . у 1 kJ1aci -36                       — 32 Y'HHi.

N2 277 стор.4З

1)    12 кг зоог= 12300г

12300: 5 820 (г) —маса л гасу,

2)    820 х 60 = 49200 (г) —маса 60 л гасу;

49200г = 49 кг 200г

           : 49 кг 200г маса 60           гасу

 287 стор 45

Уранц1

Увечер(25 л

Розв ' язання

1)         25-3 = 22 (л) —подвоене менше число,

2)         22 2 = 11 (л) —дае корова

З) 11+ 3 = 14 (л) —дас корова  корова дае 14 J1iTPiB молока, а -1 1

Запиши довжину колод у сантиметрах. 10 м- 1000 см

7 м- 700 см

1) 000 8 = 125 (см) — шматки колоди; 2) 700 5 - 140 (см) —шматки колоди.

125 см— 1 М 25 см

140 см— 1 м 40 см

I м 40 см > 1 м 25 см шматки        колоди У 335 огор . 53

250 м.

 Подив\ться на малюнок. Кожну частину дроту позначили  Коли забрати 10 м., BCi три  будуть мати однакову довжину.

 Чи можемо ми визначити яка довжина BCix цих

            (Можемо,                      ciei довжини дроту

 Про що цього? (Про довжину кожно: частини дроту)

 А що означае ця (Ми визначимо довжину трьох однакових частин дроту).

> Як визначити довжину частини?  на 3  Знаючи довжину однакових частин, як визначити довжину трдгьо1• частини? (Додати 10 MeTpiB).

1)  250-10 = 240 (м) —довжина 3 однакових частин;

2)  240 3 80 (м) — довжина 1 та 2 частини; З) 80 + 10 = 90 (м) —довжина З частини довжина частини дроту 90 MeTpiB.

 405 ст.63

Допомога

1)     4 м 9 дм + 9 м 8 дм = 13 м 17 дм — 14 м 7 дм — за 2 секунду

2)     14 м 7 дм + 9 м 8 дм = 22 м 25 дм — 24 м 05 дм — за З секунду

3)     4 м9дм + 14 м7 дм + 24м5 дм = 42м21 дм — 44Ml дм — за З сек. 44 м 1 дм  парашутист за З секунди.

416 ст 65

- Наливаемо в 10 л  по 3 л. У ньому залишасгься ще на I л води. Наберемо вчегверте повний поки BiH не наповниться доверху залишиться 2 л води Виллемо всю воду з i в порожню посудину переллемо 2 л води з

Наллемо в  ще по 3 л , разом це становитиме 8 л. По ходу MipkYBaHb вчитель заповнюе таблицю

ЛЬ 427 стор„ 69

Допомога для середнього учня

План розв'язування

Яка маса половини цукерок ?

 Яка маса BCix цукерок?

 Яка маса порожньо\ коробки?

Допомога для учня.

1)     550 — 300 = 250 (г) — маса половини цукерок

2)     250 х 2 = 500 ( г) —маса цукерок

3)     550 — 500= 50 (г) — маса порожньо\ коробки маса порожньо\ коробки 50

у 453 сто 71

Таблицю заповнюемо в  MipkYBaHb, Порядок заповнення показано номерами

 Якщо жодна з них не тримала , назв яких походить \м'я то в таблицю записусмо — «Hi».

Що говориться в З  (Що Маргарита тримала не

У стовпчику Маргарити вже е 2 «Hi» .отже вона тримала не маргаритки i не , а значить мальви — (5). У рядку «мальви» с «Hi» i «так», отже, у ставимо «Hi» (6) i т.д.

        Мальва тримала           Маргарита — мальви,

маргаритки.

N2 626 стор.96

Покажемо на двох   рух кожного велосипедиста. вони       дорогою, але  зобразити рух окремо

перший велосипедист за 2 години встиг про\хати

( на момент проколу шини)

10 х 2 20 км, а другий - 13 х 2 = 26 км

                  Отже, другий велосипедист на цей час    випередив

Першого на? (26 - 20 = 6 км). Тепер другий  з якою (4км/год,), а перший з початковою 10 км/

год. Очевидно, шо через деякий час перший велосипедист

наздожене другого?

Коли це  (Коли BiH надолужить 6 км, ix За кожну годину один наблизиться до другого на км. , яка рвниця iXHix швидкостей. Як це можна взнати? (10 - 4 = 6 км/год.). Отже,  першого велосипедиста на другого (6 км). Тобто за одну годину ними скорочуеться на 6 км. Значить через ckiJTbk11? (1 годину проколу шини). Нам треба взнати, на MiCTa це  Для цього достатньо мати час руху першого велосипедиста i його llIBl1LlkicTb його He3MiHHa, а час початку руху до становить 2 + = З год.

Отже за 3 години BiH про\хав 3() км.

Розв' язання.

         1) 13 - = 3 (км/год) - 2 велосипедиста,                                                       ] .

2) 3 х2=6 (км)

З) 10 - 4 = 6 (км/год) -  1 велосипедиста, 2. 4) 6 • 6 = (год.) — час, за який перший велосипедист наздожене другого     проколу камери.

5) 2 + 1 =3 (год.) - час руху першого велосипедиста до

6) 10х 3 = 30 (км.)

 BiH про\хав 30 км,

.М2 637 стор. 97

16 2 = 8 (P0kiB)

Семену тепер 8 P0kiB.

Конспект уроку з математики 1 клас

Тема. Таблиця  числа 6, задача на знаходження

формувати      навички розв'язувати зменшуваного, розвивати навички мислення, виховувати cTapaHHicTb.

Х Ы УРОКУ

1.  класу до уроку. сувора, й

Математика кра\на Праця тут завзята лиш спритно рахувати,

Додавати й збагнути все

Дати у нас немае?

Хто руки не

П. Контроль, та закртлення знань 1 . Усний рахунок.

Порахуйте до 20 ” ланцюжком”

20 до 1 ” ланцюжком' Ha3BiTb числа мВк 4 i 9

         Ha3BiTb BCi числа         за 5 , 8, 12.

на    Ha3BiTb найменше,

2. Робота в парах,

У  кожен учень записуе З одноцифрових i З двоцифрових (до 20) числа. Товариш у називае у свого

товариша:

числа; i найменше числа; вибраного числа.

У павука 8 очей, а у жука 2, на очей у павука, у жука. ?

3  за схемою таблицю додавання числа 6

1 234 5 6789+6 4 Вправа 'Дощик” Наприклад.

Я вважаю, що . . число 5 б'льше за 3, тому що в натуральному кожне наступне число за поперелнеЋ. Допоможи

1 + 6 = 7 2+6 = 8   4 + 6= 9 Ш. Вивчення нового MaTepia.r•y.

Вправа 1 (с. 17) YqHi усно пояснюють випадки числа 6 11 i 14

яких чисел ще можна число 6 i3 переходом через десяток? (12-6, 13-6, випадки на  Записують в зошит приклади по порядку:

13 - 6= 7

2 Первинне

               а) за вправою 2         називають

б) коментоване розв'язування

              в)                    розв' язування

Вправа Пояснюють правилькйсть виконання вправи.

4. Складання

 У

           Яку                                                        на це запитання

? На

Як

Яким прикладом запишемо розв'язання

IV Розвиток математичних знань.

Фронтальна робота над задачею 5,

Опрацювання 3MiCTY           i короткий запис на дошц1.

Було

Вийшло    -4 Залиш илося -9  на партах     паличок, вийшло з вертольота (4).      поруч     паличок, залишилося у     (9). З яких двох частин

складаеться число людей, були у вертольотЈ спочатку? (З тих, що вийшли, i з тих, що залишилися). це число на паличках.    об'еднують групи паличок).Що ви зробили з паличками? (Об еднали).То якою       розв'яжемо задачу? (додавання).

9+4 = 13 (л)

            То скЈльки                                 було у спочатку? (13).

Давайте чи правильно ми розв'язали задачу. (Було13, вийшло 4, залишилося 13 9 ). Задача розв'язана

- правильно.

V. уроку.

          Прочитати лише HOBi приклади                    числа 6.

Яка частина уроку вам була

            В чому ви              утруднення

Конспект уроку з математики 2 клас

Тема: Порядок виконання у виразах. Розв'язування задач на i зменшення числа в pa3iB.

 ознайомити i3 правилом про порядок виконання у виразах;  розв'язувати       на три складанням виразу; розвивати     мислення; виховувати почутгя взаемодопомоги, прагнень знань;

уроку

1. Мотиватя Вчитель.

У

Нам BCiM так хочеться тепла.

Давайте ж вирушим до моря,

Ну що,

Ви спитаете ”Чому до моря? ” Погляньте на карту. Ви бачите, що вода займае 71     земно\   А нашими помјчниками у   будуть   пам'ять, Мислення,   та взаемодопомога. Подорож починаеться.

давно уже людям yciM , Що 9 помножить на 3 - 27.

I кругом в Михася голова - 4 на 8. то це 32.

4 поиножить на 7 - 28

А 40 - це 5 помно)кигь на 8. - Ну, добре, не буду вже питати

Але пам'ятай, треба завжди все вчити.

Без знань в цьому CBiTi не можна прожити

Ш. Вивчення нового Вчитель.

• Усний рахунок нам стане в  буде легше нам справлятися з роботою, бо повторимо Ha6YTi знання. А зараз рушаймо

yci! Коник здалека.

що тут небезпека!

        Щось                 вам треба узнати,

Тож будьте з думками, Ось тема уроку. Вона перед вами.

 вирази i Тх на стовпчики. з дужкамиодного ступеня

35     - ( 40- 12) 40 - 12 + 8 20 +4 х 7 36 . ( в - 9) 12 : 3 х 8 24 - 8 : 4

Вчитель.

вирази на  обчислюються за певними правилами. Одне правило ми знаемо.

а) прочитайте правило М24

36     .

б) С й правила порядку виконання , але ми ними ще не користувалися.

Правила           , 2,

40 - 12 + 8 = 36

в) Правило N2 3

20+4х7 =48 24- 8 : 4=22

3. Первинне

Вчитель.

Книги морська глибина,

                          Хто в них          аж до дна,

Той, хоч i труду мав досить, перла виносить!

Так сказав про книги Т.Я Франко. Тож давайте i ми з вами за перлами.

а) лг2 899 - самост(йно б) Давайте  як  порядок

ЗАПАМ ЯТАй

36 0+3 х2= 15

36 (9 + 3)х7

Висновок:  порядок  - значення виразу.

IV. Розв'язування задач.

1. Задача 900

Розв'язуючи приклад чи задачу,

Т и, друже, не

Спочатку гарно подумай,

                А          вже пиши,

         Що ми можемо сказати про                                  банки?

взяли        а      п'     банок ?  Чи можемо ми одразу знайти,    всього соку розлили?

Чому ?

 А чи зможемо ми знайти, соку у BCix банках?

                         18       10

3 х 6 + 5 х2 =28

2,

Раз присядьте, два присядьте. I за перти тихо сядьте.

     З. Розв'язання          Уд 901,

Якою

Чому ?

виразом (1 ряд) по (2 ряд)

1) 5 х 4 = 20 (п.) 2) 5 + 20 = 25 (п.)

Вираз: 5+(5 х 4 ) = 25 (п.)

25

      4. Задача з                  навантаженням.

Восьминоги                         взутися у  чоботи.

водолаза, щупальця?

1) 4 х 8 = 32 (щ.) - всього роззути 16

       V.                  уроку.

-   Про що нове ви      на  

-   ЯКИХ    MOPiB

-   Що вам допомогло виконувати завдання правильно?

VI Домашне завдання.

N2 902 (1 ряд    2 ряд виразом). N2 903.

Конспект уроку математики у З

Тема. Додавання i  виду 230 + 70 , 200- 60.    3 числами.

розширити знання    про круглих чисел, формувати числами, розв'язувати       на третього доданка , розвивати       мислення.

I.                                                                                            класу до роботи.

II.                                                                                       спорних знань,

1. Вправи для усного рахунку(мегод проблемно-пошуковий().

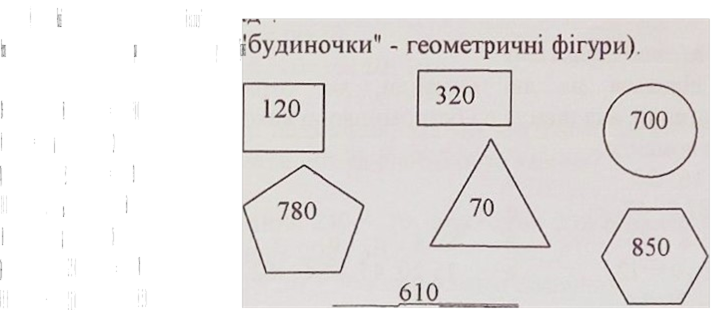
860- 250 =660.

по виходять до дошки, пояснюють розв'язання i ”поселяють” вираз у ”будиночок” - геометричну i дають визначення кожн{й з них. Вправа

Приклади

-            Перший вираз я поселю у круг, тому що його результат 700, а число 700 живе у kPY3i.

-            Другий вираз у квадрат, 60 його результат 120 , а в живе число 120,

-            Квадрат - це прямокутник, який мае 4  за довжиною сторони i      кути.

б) вправа (вивести 3ak0H0MipHicTb i знайти ”зайве” число, пояснити чому).

340, 547, 24, 825, 326

числа.

 У другому рядку - число 311, 60 воно непарне, а решта числа.

У третьому рядку-812, тому що воно не кругле, а решта числа.

Вправа  передають  пояснюють розв'язання кожного прикладу).

Метод пщиДенту.

      Клас  на             команди,      отримують завдання.

Перемагае та, яка швидше i безпомилково виконае завдання.

Перша команда.

9 х4 - д

8   х7 -

9   х (13-

   64 8+9х6=62       

Вчитель. Як пишеться це слово?

(Слово дев'ять пишеться з апострофом). - Коли ставиться апостроф?

     повторюють правила написання       з апострофом).

Друга команда.

   8х4- 12=20             д

с ь я д с т е я 88 81 20 1749 33

   63 : 9+9х9=88          Ь

         б)       записують рядок цифри 9, пояснюючи з яких

вона складаеться.

в) записати BCi цифри першо\ COTHi, мають в  цифру 9.

IV. Оголошення теми i мети уроку.

 ми будемо додавати числа виду 230 + 70, 200 — 60, виконувати числами.

(Пояснення  проходить у

” Учитель-учень” у межах проблемно-пошукового 23() + 7() = ?

Вчитель,

Як можна виконати додавання?

1                     уч.

Можна додавати по 10 230 -4Вчитель.

Можна i так виконати додавання, але ми затратимо багато часу. Хто може запропонувати розв'язання?

2                     уч.

Щоб виконати додавання 230 + 70,  230 розкласти на суму розрядних 200 i 30.

Отримасмо вираз 200 + 30 + 70 i застосуемо сполучну додавання.

200 + (30 зоо отже, 230 +70 = 200+(30 +70) = 200 + 300.

Вчи тель.

                        яким способом   виконати додавання?

(еЦруги.м способом).

Розглянемо другий приклад. 200 - 60 = ?

Вчите.ть.

Як можна розв'язати цей приклад?

        Можна  по 10.Але цей           займае багато часу.

Для цього noTpi6H0 200 розкласти на суму чисел 100+100, отримаемо 100 + 100 — 60. Застосуемо сполучну

Отже: 200 - 60 = 100 + (100 - 60) = 140

Вчитель. Яким способом  виконати додавання i  круглих трицифрових чисел виду 230 + 70, 200 — 60

 Звичайно, другим способом ,розкладаючи числа на суму розрядних

V.

способом розв'язання таких

знання.

а       час - у 5 вдихне людина за 2 хв.   час

                   Ходьба -      9л

?

час ходьби?

час

(Hi, 60 не знаемо, Як за 1хв?

План розв'язування

1     , Знаходимо   людина вдихае  за 1хв.       час застосовуочи дне множення

Знаходимо склльки людина вднха€ повттря за 2 хв       час 6iry. застосовуочи   додавання.

Розв'язання

(C11,1bHi розв'язують задачу складанням числового виразу, а

- по              з поясненням

1)    9 х5=45 (л) - вдиха€ за хв. час 6iry

2)    45 +45= 90 (л) - за 2 хв

Вираз. 9х5 + 9 х 5 = 90 (л) людина вдихае 90 л       за 2 хв час

УЛ.  робота.

5м-20 см = 480 см = 4м 80 см

З кг - ЗОО г = 2700 г-=2кг 700г

2     год 20 хв + 40 хв = 180 хв = З год

ив. 1 кг - ЗО г= 97О г  м 20 см +80 см = 200 см = 2 м

3     год- год 20 хв = 100 хв = 1год 4() хв.

Вправа

У                   геометрй“

-    це     . яка мае початок.

-    це частина прямо\ , обмежена з двох CTOPiH.

-    це     , якою

-це частина прямо1 , обмежена з двох CTOPiH.

Накресли вертикально.

; Накресли горизонтально.  Накресли      похило.

VI.                     уроку.

-                                                 знання нам допомогли виконати завдання?

-                                                 Знання     трицифрових чисел.

-                                                 виконувати додавання i круглих чисел виду 230 + 70 , 200 - 60.

-                                                 перетворювати iMeH0BaHi числа i виконувати ;'lii з ними.

-                                                 Застосування знань з час виконання завдань з математики

VII. Домашне завлання.

Скласти задачу , обернену до задач\ 617 на с.95 п\дручника, Скласти три приклади на з числами.

Конспект уроку з математики 4 клас

Тема Знакодження i3 CTOPiH прямокутника за його площею i другою стороною.

       задачам на сп{льну роботу              iMeH0BaHHx чисел.

Систематизувати знання      про знаходження прямокутника;  формувати      знаходити одну i3 CTOPiH прямокутника;  формувати     навички       та розв'язувати    задачам на   роботу,  розвивати навички YCH0i      мислення;  Виховувати cTapaHHicTb,

План уроку. момент.

Математика - наука точна i серйозна.

прожить без       нам HaBiTb дня не можна.

11. Контроль, та знань.

1. Усне обчислення.

1)       Гра ”День та

На слово                       кладуть голови на парту i заплющують

 Вчитель                       диктуе ”Ланцюжок”

знаходять 1х значення.

Коли вчитель промовляе слово ”День” голови i  руки. Один учень називае остаточну Так

2)       48 . 3 х 4 (64) 48: 4 х 5(60)

      48 : 2 хз (72)                    48: 6х 9 (72)

3) а) Довжина прямокутној• форми 5 м, ширина - 4м. Знайги площу (20 м кв.)

б) Довжина прямокутника 1 Ом , ширина - на 2 м менша. Знайти площу прямокутника (80м кв)

в) Довжина прямокутника ТОм              ширина становить 1/2

довжини. Яка площа прямокугника? (50 м кв)

г) Площа квадрата 49 м кв Знайти сторону квадрата (7 м) 4) Завдання для опитування (групами)

Картка (для                i3 високим piBHeM знань)

1. Прямокутник i квадрат мають однакову площу. Довжина прямокугника 12 м, а ширина - у 4 рази менша. Знайти сторону квадрата. (7 м)

Bka3iBka. час знаходження сторони квадрата подумай , яке число при само на себе лае число, що виражае площу квадрата (6 м).

2, 24 Т + 9 ц . З ( 8 т 3 ц)

    Картка 2 (для          i3                piBHeM знань)

1)        Площа    72 арн 1/6      займае сад, а 1/3 -город.

Яку плошу займають сад i город разом? (36 apiB)

2)        4 [тн 20 К 7 (60 к)

   Картка З ( для     i3 cepeAHiM та початковим piBHeM знань)

ПокЯдуй прямокугник 3i сторонами З см 5 мм i 8см 5 мм

Обчнслн йото периметр площу (24 см. 2975 мм кв)

2)                    15 к м 5 (25          7 S к)

Н. 0' олошення теми i метн уроку.

- Сього,лн' ми бу.асмо знахо:ипи одну i3 сторт прямокутника за по: о площею тломо дрыхмо стороною

1ll. Внвчення ново! о Marepia-ay.

Тл ерам инна вирава “ Мо 'ковий

Ареол внатн на вашу 4',мку. [1106 знайгги площу

iaet     Жоана з них не в р.ввнватн [10ttepeat31

прямоку•тника досить знань про периметр ловжину ВСХ сторш знатл' ловжину дво\ сгор'н перетворення менованих чисел

г  знати таблицю Mip дов)кннн yqHi aHaJ1i3Yt0Tb записи i роблять висновок.

2       Ознайомлення з правилами знаходження i3 прямокутника за йото площею i Bi!l0M0to друого стороною, (за вправою 508 (1)

 Чому лорнинос прямоку\мнка'? (лобугку двох чисел). [Цо позначают•ь числа (ловжнну i ширину)

 Тодж можна знати илоту (лобуток) i одну i3 стор'н” (Можна 3Haii1M другу ii010 сторону).

3       Закрнтлення вивчснсмхз MaTepiaJIY

Учвям лають прямокытннки pi3H01 величины

Вавлавнч I   и ловжнну ширину прямокугника . Знайти площу.

,

(з лопчним наважтаженням)

прямокугника ?

ми обчислили

24 дм 72

на дм менша

ширини? (Так,

разом 0 (24 ' 2 = вона була такою як

— 8 см). А

> Що тепер можна визначити ? (Довжину 4 + 4 — тепер обчислимо площу 8 х 4 = 32 дм кв.

IV. Розвиток математичних знань.

Задача,                                 на              роботу. (N2507)

1.        Повторення 3MiCTY    i заповнення таблит

2.        Складання плану розв' язування План.

1.                                                  ciHa дають 3e6pi на 1 день?

2.                                                  ciHa дають   на I день.? З.         ciHa дають 3e6pi i       на 1 день?

     4. На                         вистачить yciM тваринам 450 кг ciHa?

    Завдання:                 розв язання з поясненням.

Учням з високим piBHeM знань можна запропонувати записати розв язок  виразом. спробуйте скласти обернену задачу .

2. чисел. Вправа 510.

Вчитель звертае увагу на те, що при 36 т 9 ц на З ц ми pa3iB З ц у числј 36 т 9 ц.

Запис. Збт9ц : З ц= 123

4 ц 8 кг : 8 кг = 408 кг : 8 кг = 51

                  15 км 250 м : 5        3050

6 м 24 см : 4 см = 156 V. Пјдсумок уроку

-   Чи сподобався вам урок?

-   Що яталося?

-   Вправа речення:” Цей урок мене навчив

70

Список

 Ьегданович м В , Козах М.. Коваль Я Методика викладання математики в початкових класах- К А С К , 1998

Богданович М В Математика  З клас, 4 клас,-К: 0cBiTa. 2004

3             Богданович МВ Математика (п{дручник), 1 клас, „ клас,-К. 0cBiTa. 2005

4             Початкова ocBiTa. Методичний порадник. Випуск 1.2006 -572 4.

5             Початкова школа.-2004 У212

6             Початкова школа.-2005 JY2N2 2.5.9.

7             Програма для  школи, 3-4 клас.-Кх Початкова школа 2006.

S Богданович. Методика розв'язування задач в — К. ' АСК. 1990.

9. Корчевська О., Козак М Робота над математичними задачами в 4 класг  «Астон». 2002 р.

змтст

Встут

I. Методика розв'язування задач з                 навантаженням.         4

IV.                                              та розв язування задач з навантаженням

25

V.                                                  та розв язування задач з навантаженням

31

VI.                                              та розв язування задач з навантаженням

35

VII.                                          та розв язування задач з        навантаженням

43

VIII.                                      Конспекти YP0kiB математики

1.                   Конспекти YP0kiB математики у        51

2.                   Конспекти YP0kiB математики у 2     54 З. Конспекти YP0kiB математики 60

              4. Конспекти yp0kiB математики у 4                                      66

72