Геометричні нерівності

Зміст

       Вступ ____________________________________________________________         3

     Розділ І. Застосування нерівності трикутника до розв'язування         змістовних задач __________________________________________________           4

     Розділ ІІ. Використання числових нерівностей при доведенні             геометричних нерівностей _________________________________________      6

        Розділ ІІІ. Геометричні нерівності на математичних олімпіадах _______           9

3.1. Нерівності між основними елементами трикутника і чотирикутника ___            9

3.2 Нерівність Герона ____________________________-______________________       10

3.3 Нерівність Ейлера __________________________________________________        11

3.4 Нерівність Птоломея _______________________________________________          11

Список використаних джерел ___________________________________________        13

Вступ

Серед наук, які мають вирішальний вплив на зростання технічної озброєності, безперечно, важливе місце належить математиці. Ця наука має численний арсенал засобів, які дають можливість розв'язувати різноманітні задачі. Одним з них є нерівності. За допомогою нерівностей формулюється багато задач, виражається більшість результатів математичних досліджень.

З нерівностями, як правило, пов'язують задачі двох типів: 

1) знаходження умов, за якими дана нерівність перетворюється в істинне висловлення (розв'язання нерівності); 2) доведення того, що за певних наперед заданих умов дана нерівність перетворюється в істинне висловлення. Такі задачі виражають суть багатьох проблем наукового і практичного характеру.

Теорія нерівностей відіграє в математиці велику роль, а деякі її сучасні галузі, зокрема лінійне та нелінійне програмування, теорія ігор, дослідження операцій тощо, повністю грунтуються на цій теорії.

Розглянемо досить широкий клас цікавих і важливих для застосувань нерівностей, доведення яких пов'язане з геометричними міркуваннями і які на цій підставі називатимемо геометричними.

Розділ І. Застосування нерівності трикутника до розв'язування змістовних задач

Задача 1. У трикутнику довжини двох сторін відповідно дорівнюють 3,14 та 0,67. Знайти довжину третьої сторони, якщо відомо, що вона виражається цілим числом.

Розв'язання. Якщо ця довжина дорівнює а, то a<3,14+0,67 та  а>3,14-0,67. А отже, а=3.

Задача 2. У площині взяли довільний трикутник ABC і коло радіуса 1. Довести, що на колі знайдеться точка, сума відстаней від якої до вершин трикутника не менша 3.

Розв'язання. Нехай М та N - дві діаметрально протилежні точки на колі.

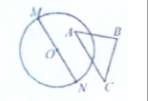Тоді MN=2. А отже, MA+AN2, MB+BN2,

MC+CN2. Додавши ці нерівності, одержимо (MA+MB+MC)+(AN+BN+CN)6.

А тому, принаймні в одних дужках сума не менша від 3.

Задача 3. Доведіть, що медіана трикутника менша півсуми прилеглих до неї сторін.

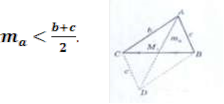
Доведення. Згідно рисунка, доведемо, що

Продовживши медіану вдвічі, отримаємо паралелограм АВDС,  і b + с > 2т_а (за нерівністю трикутника для АСD), звідки, 

що й потрібно було довести.

Задача  4. Доведіть, що для суми медіан будь-якого трикутника справедлива наступна подвійна нерівність: р < т_а + т_ь + т_с < 2р.

Доведення. Згідно із попередьою задачею, 

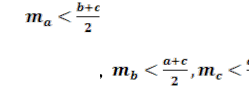
Додавши ліві і праві частини нерівності, отримаємо:

т_а + т_ь + т_с < 2р. Далі для АМВ: т_а + т_ь >c. 

Далі для CМВ:  т_с + т_ь > а, СМA: т_a + т_c >b.

Додавши ліві і праві частини нерівностей, отримаємо:

 (т_а + т_ь + т_с) > 2р або p< т_а + т_ь + т_с.

Що й потрібно було довести.

Задача 5. Доведіть, що відрізок між вершиною і протилежною стороною трикутника менший найбільшої з двох інших сторін.

Доведення. Нехай в АВС b>с і АЕ ― даний відрізок.

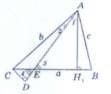Доведемо, що АЕ<b. Проведемо висоту АН₁,.

1+С=90° (з АН₁С). Тоді 2+С<90° і 3<90°, оскільки

3=2+С (зовнішній для АСЕ). Значить, і вертикальний з ним 4<90°. Отже, висота в АСЕ потрапить на продовження. АЕ. У прямокутному АСD АC>АD (гіпотенуза більше катета) і тим більше АC>АЕ, тобто АЕ< b, що і потрібно було довести.

Розділ ІІ. Використання числових нерівностей при доведенні геометричних нерівностей

Наведемо числові нерівності, які використовуватимемо далі при доведенні геометричних нерівностей:

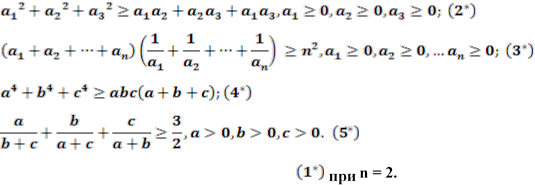Проілюструємо застосування нерівності

Задача 1. Довести, що в трикутнику ABC

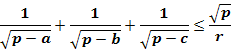
(a. b, с — сторони трикутника ABC, р — півпериметр; r — радіус вписаного кола).

Доведення. Перетворимо ліву частину нерівності

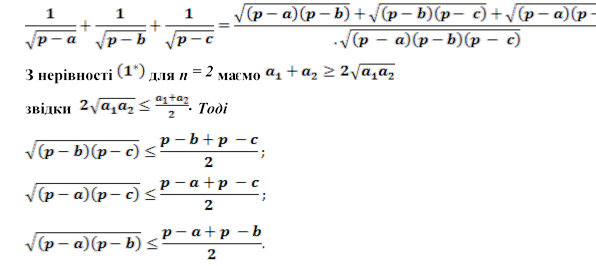
Додавши три останні нерівності, дістанемо

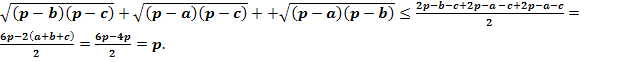
 Позначимо S площу трикутника ABC. Тоді

Задача 2. Довести, що в трикутнику ABC a⁴ + b⁴ + с⁴  16S². 

Доведення. З нерівності , маємо а4 + b⁴ + с⁴  abc(a + b + c) = , бо  R2r.

Задача 3. У трикутнику ABC — висоти; 

 — відстані від основ

бісектриси кутів трикутника до його сторін. Довести, що:

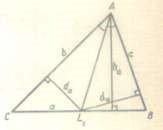
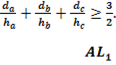                Доведення.        — бісектриса кута ВАС трикутника                             Рис. 1

ABC (рис. 1). Позначимо

S, S₁, S₂ площі трикутників ABC, AL₁B, AL₁C.  Тоді S = S₁ + S₂,

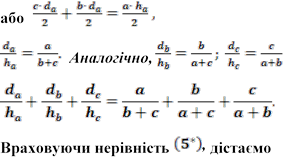  де a, b, c — довжини сторін трикутника ABC. Отже,

і

Задача 4. Довести, що в трикутнику  ABC 

Доведення.

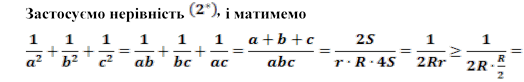
Задача 5. Довести, що в трикутнику ABC

Доведення.

З нерівності   

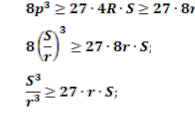
Задача 6. Довести, що y трикутнику ABC

1)                   

 Доведення.

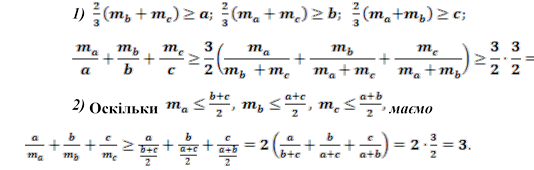
Розділ ІІІ. Геометричні нерівності на математичних олімпіадах

3.1. Нерівності між основними елементами трикутника і чотирикутника.

Основними елементами трикутника та чотирикутника є їхні сторони і кути. Спочатку розглянемо ті співвідношення (нерівності) між цими елементами, які вивчаються у шкільному курсі геометрії. А далі розглянемо класичні геометричні нерівності та ознайомимось із методами їх доведення.

•                     Якщо А, В і С — довільні точки площини, то

Рівність у цій нерівності досягається тоді і тільки тоді, коли точка В належить відрізку АС.

Це твердження називають нерівністю трикутника.

•                     У будь-якому трикутнику проти більшої сторони лежить більший кут, і навпаки.

Тобто якщо у трикутнику ABC має місце нерівність , то ВС > СА, і навпаки.

•                     1) Якщо а, b і с — додатні числа, для яких виконуються нерівності а < b + с, b < с + а і с < а +b, то існує трикутник, довжини сторін якого дорівнюють a, b і с.

2)                  Побудувати трикутник, довжини сторін якого а < b < с, можна лише тоді, коли виконується нерівність с < а +b.

3)                  Перетворення Раві.

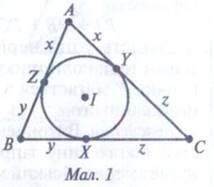 Побудувати трикутник, довжини сторін якого а, b, с, можна лише тоді і тільки тоді, коли існують такі додатні дійсні числа

x, y, z, щo  

a=y + z, b = z + х і с = х + у. Геометричну суть чисел х,  у і z видно з

мал. 1.

При цьому  

 — де півпериметр трикутника ABC;

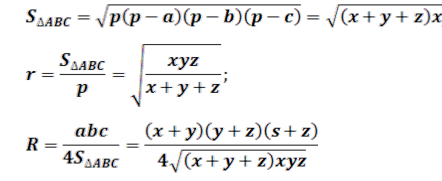
3.2 Нерівність Герона. Для довільного трикутника ABC виконується нерівність:

, де ВС=а, СА = b, АВ = с.

Доведення. Застосуємо перетворення Раві. Оскільки 

, то ліва частина матиме такий

вигляд:

, а

права частина буде такою:

abc = (х + у)(у + z)(z + х). Отже, нерівність, яку потрібно довести, еквівалентна такій нерівності:

.

Справедливість цієї нерівності випливає з нерівності між середніми арифметичними і середніми геометричними: 

 Перемноживши їх, одержимо нерівність, яку потрібно було довести.

3.3 Нерівність Ейлера. Для довільного трикутника ABC виконується нерівність:  де R — радіус описаного кола, а r — радіус вписаного кола в трикутник  ABC. Рівність у цій нерівності

досягається тоді і тільки тоді, коли трикутник ABC — рівносторонній.

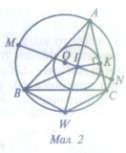
Доведення. Нехай W— середина дуги BС описаного кола навколо трикутника ABC, О — центр цього кола, I — центр вписаного кола в трикутник ABC,  К — точка

дотику цього кола зі стороною АС (мал. 2).

Оскільки W — середина дуги ВС, то AW— бісектриса кута ВАС, тобто точка I лежить на цій бісектрисі. При цьому WB= WI= WC. 

Проведемо діаметр MN описаного кола, який проходить через точку I. Тоді за теоремою про пропорційність відрізків у колі маємо:

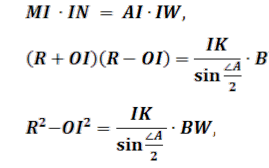
За теоремою синусів з трикутника ABW знаходимо:

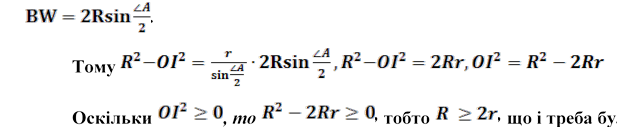
довести.

3.4 Нерівність Птоломея. Для довільного опуклого

чотирикутника ABCD виконується нерівність

.

Рівність у цій нерівності досягається тоді і тільки

Мал. 3

тоді, коли чотирикутник АВCD можна вписати в коло.

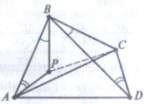
Доведення. Проведемо через вершини А і B чотирикутника АBСD

такі промені АР та ВР (мал. 3), щоб .

Тоді з подібності трикутників АВР і DВС (за двома кутами) маємо:

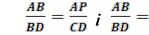. Звідcи випливає, що  

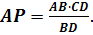
Далі, трикутники РВС та АВD — подібні (за двома сторонами  і кутом між ними ). 

З подібності цих трикутників знаходимо тобто  

За нерівністю трикутника маємо: .

Тому   

Звідки випливає, що , що і треба було

довести. Знак рівності досягається лише тоді, коли точка Р лежить на відрізку АС. Але тоді , тобто точки А, В, С, D лежать на одному колі.

Список використаних джерел

1. І. А. Кушнір Методи розв'язання задач з геометрії  //Київ АБРИС 1994. 2. Ш. Г. Горделадзе, М. М. Кухарчук, Ф. П. Яремчук //Збірник конкурсних задач з математики, Вища школа, Київ-1976.

3.   Вишенський В. А., Ядренко М. Й. Вибрані задачі з алгебри й геометрії //К., Вища школа, 1972.

4.   Яремчук М.Л., Попруженко М. Г. Збірник геометричних задач.

Планіметрія//К., Радянська школа, 1996.

5.   Федак І. В. Розв'язування рівнянь. Доведення нерівностей. Посібник для підготовки до математичних олімпіад у 9-10 класах //Тернопіль, 1998.