Урок на тему "Прикладні задачі. Розв’язування трикутників."

Про матеріал

Мета уроку: Формування вмінь та навичок розв’язування трикутників, застосовувати набуті знання для розв’язування прикладних задач. Закріпити основні алгоритми розв’язування трикутників, теорему синусів та косинусів. Виховувати наполегливість, інтерес до математики та позитивну мотивацію до навчання.

Перегляд файлу

Тема уроку: Прикладні задачі. Розв’язування трикутників.

Мета уроку:

Формування вмінь та навичок розв’язування трикутників, застосовувати набуті знання для розв’язування прикладних задач.

Закріпити основні алгоритми розв’язування трикутників, теорему синусів та косинусів. Виховувати наполегливість, інтерес до математики та позитивну мотивацію до навчання.

Тип уроку: Застосування здобутих знань.

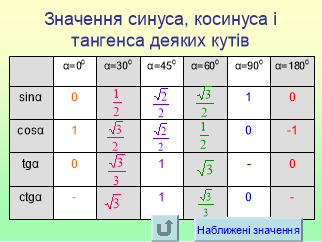
Обладнання: Презентація Microsoft PowerPoint. Таблиця синусів і косинусів, таблиця тангенсів.

Хід уроку:

І. Мотивація навчальної діяльності.

Організаційні питання, щодо початку уроку.

Вчитель повідомляє тему уроку, мету.

ІІ. Актуалізація опорних знань учнів.

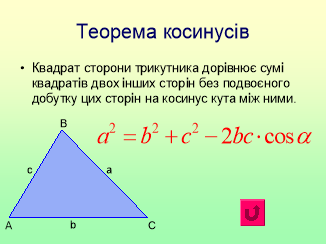
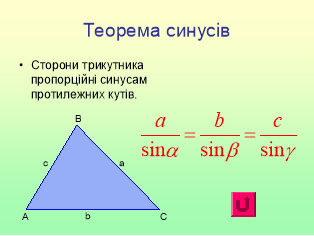
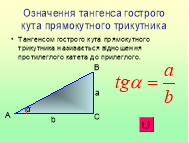
	Бігле повторення теорем синусів та косинусів, наслідків теорем. Якщо в трикутнику АВС відомі дві сторони та кут між ними, то третю сторону можна знайти за теоремою… Якщо в трикутнику відомі сторони, то кути можна знайти…
	Якщо в трикутнику АВС відомі два кута і одна сторона, то ще одну сторону можна знайти за теоремою… Якщо в трикутнику АВС відомі дві сторони і один кут, чи завжди можливо знайти інші кути?
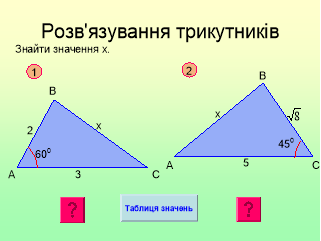
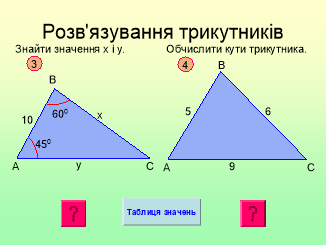
	Розв’язування задач за готовими рисунками. (Протягом всього уроку можливе використання довідки, щодо вибору теореми та значень синуса, косинуса, тангенса деяких кутів та фрагменту таблиці Брадиса – гіперпосилання презентації)

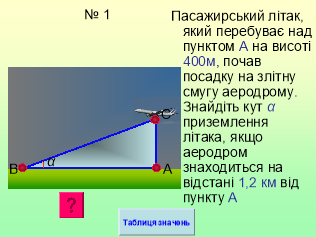
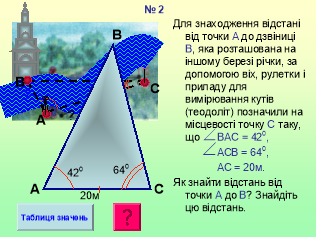
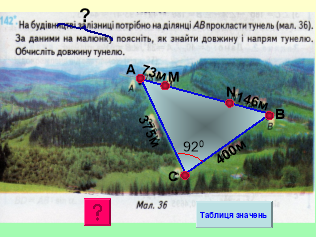
ІV. Розв’язування прикладних задач.

Які задачі називають прикладними?

Застосуй на практиці!

При розв’язувані задачі

№ 1 посилання на означення тангенса.

Де можна зустріти задачі на розв’язування трикутників та застосування теореми синусів та косинусів?

Наприклад, при знаходженні відстані до точки, яка знаходиться в недоступному місці.

При розв’язуванні задачі складається алгоритм розв’язування задачі та записується розв’язання на дошці.

В разі необхідності використовується посилання (для групи слабо підготовлених учнів)

Задача № 142 розв’язується усно, записати розв’язання та виконати обчислення задається додому.

Робота з підручником

Учні задають питання, що виникли під час розв’язування задачі.

Відповідні записи на дошці та в зошиті.

Резервна задача № 174 може бути запропонована групі підготовлених учнів для розв’язування в зошиті.

V. Підсумок уроку. Оцінювання учнів.

Висновки:

Щоб визначити відстань між доступною точкою і недоступною точкою, необхідно вибрати другу доступну точку…
Щоб знайти відстань між двома недоступними точками, необхідно вибрати дві доступні точки…
Щоб знайти висоту предмета, основа якого недоступна, необхідно вибрати дві доступні точки…

В підсумку уроку вчитель нагадує що саме на уроці було зроблено і повторено, пояснює домашнє завдання, дає оцінку всьому класу та називає оцінки конкретним учням.

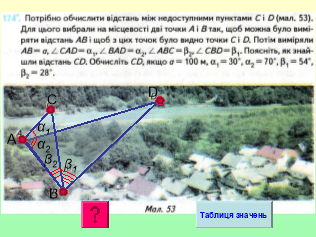
Домашнє завдання:

П. 5 – повторити розв’язування трикутників та прикладні задачі на знаходження відстаней . Записати розв’язання задачі №142, скласти дві прикладні задачі на знаходження відстані між двома доступними точками (якщо безпосереднє вимірювання неможливе) та відстані до недоступної точки.

Середня оцінка розробки

Структурованість

4.0

Оригінальність викладу

4.0

Відповідність темі

4.0

Загальна:

4.0

Всього відгуків: 1

Оцінки та відгуки