Матеріал для факультативу: "Монотонні послідовності і функції"
Монотонні послідовності
і функції
РОЗДІЛ I. МОНОТОННІ ПОСЛІДОВНОСТІ.................................................. 4
РОЗДІЛ II. ЕЛЕМЕНТАРНІ ВЛАСТИВОСТІ МОНОТОННИХ ФУНКЦІЙ. 12
2.1. Означення та найпростіші приклади................................... 12
2.2. Монотонність породжує монотонність............................... 14
2.3. Інші приклади монотонних функцій................................... 16
2.4. Елементарне дослідження функцій на монотонність...... 20
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ........................................................ 21
ВСТУП
Послідовність явище унікальне. Історія їх виникнення губиться в глибині віків.Вже у клинописних табличках вавилонян, у єгипетських папірусах датованих ІІ тисячоліттям до н. е. зустрічаються задачі на арифметичну та геометричну прогресії. В продовж століть людей приваблювала внутрішня гармонія і строга краса числових рядів. Числові послідовності зустрічаються часто і не лише в математиці а й в фізиці, біології, найчастіше-монотонні.
Монотонні послідовності відіграють важливу роль у математичному аналізі. Дослідження функції на монотонність є істотною частиною побудови її графіка-воно дає змогу знайти точки екстремуму і визначити характер зміни функції.
Монотонні функції широко використовуються у теорії міри і теорії ймовірностей, при доведенні нерівностей, їх розв’язуванні, розв’язуванні рівнянь.
В підручниках з математики базового рівня дана тема розкрита недостатньо, а в деяких носить лише допоміжний характер, хоча розв’язання більшості рівнянь та нерівностей можна обґрунтувати монотонністю функцій, які входять в них.
В роботі висвітлено теорію монотонності послідовностей та функцій, а також показано практичне застосування монотонності послідовності та функції.
РОЗДІЛ I. МОНОТОННІ ПОСЛІДОВНОСТІ1.
1.1. Приклади
Нагадаємо, що послідовністю є відображення, яке кожному натуральному числу п ставить у відповідність деяке дійсне
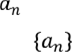
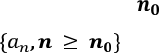 число
. Позначається послідовність так:
число
. Позначається послідовність так: ![]() ,
або коротше: Нумерація членів послідовності може починатися з
довільного номера ; такі нескінченні набори чисел позначають , .
,
або коротше: Нумерація членів послідовності може починатися з
довільного номера ; такі нескінченні набори чисел позначають , .
Будь-яку послідовність можна подати як нескінченний набір за-
нумерованих чисел ![]() …Якщо ці числа
…Якщо ці числа
упорядковані за величиною, тобто більшим номерам відповідають більші (менші) числа, то така послідовність називається монотонною. Дамо точні означення..
Означення 1. Послідовність ![]() називається
зростаючою,
називається
зростаючою,
якщо ![]() для
для
кожного п є
N, і називається спадною, якщо ![]() для кожного nєN.
для кожного nєN.
Означення 2. Послідовність
![]() називається неспадною, якщо
ап+1 ≥ ап для всіх п є N, називається
незростаючою, якщо
називається неспадною, якщо
ап+1 ≥ ап для всіх п є N, називається
незростаючою, якщо ![]() ап для
всіх п єN
ап для
всіх п єN
Означення 3. Послідовність
![]() називається монотонною, якщо
називається монотонною, якщо
вона належить одному із зазначених вище чотирьох типів. Послідовність називається строго монотонною, якщо є або зростаючою, або спадною.
Найпростішими прикладами монотонних послідовностей є арифметична прогресія, а також геометрична прогресія зі знаменником q >0.
Наведемо складніші приклади монотонних послідовностей.![]()
 Остання нерівність правильна, оскільки
Остання нерівність правильна, оскільки
Таким чином, послідовність {![]() }
спадна.
}
спадна.
Приклад 2. Задамо послідовність рекурентним
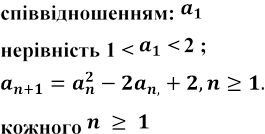 - довільне число, що задовольняє
- довільне число, що задовольняє
(1.1) Доведемо спочатку, що для
1 < ![]() < 2. (1.2)
< 2. (1.2)
Скористаємося методом математичної індукції. Якщо п = 1, то нерівність виконується за умовою. Нехай вона справедлива для
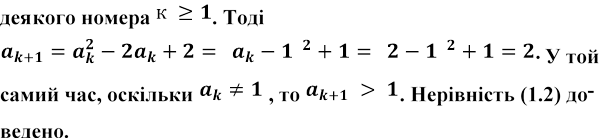
Перейдемо до дослідження монотонності заданої послідовності.
Утворимо різницю
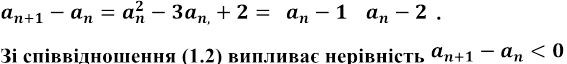 ,
,
![]() .
.![]()
Отже, спадання послідовності { } доведено.
![]() Означення 4. Послідовність
називається зростаючою
Означення 4. Послідовність
називається зростаючою
(спадною), починаючи з номера т, якщо послідовність
{![]() } зростає
(спадає).
} зростає
(спадає).
Іншими словами, послідовність ![]() зростає,
починаючи з
зростає,
починаючи з
номера т, якщо виконуються нерівності: ат < ат+1< ат+2 <...
Задача 1. Знайти найбільший член послідовності
![]()
Розв'язання
Як і в прикладі 1, складемо відношення двох сусідніх членів послідовності. Після очевидних спрощень маємо:
![]()
Звідси випливає, що
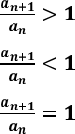
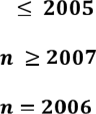 , коли n ,
, коли n ,
, коли ,
, коли ,
Таким чином,
послідовність ![]() зростає до номера 2006 і, починаючи з
наступного номера, спадає.
зростає до номера 2006 і, починаючи з
наступного номера, спадає.
Найбільшими є два члени послідовності:
![]() .
.
Можна запідозрити, що будь-яка послідовність є монотонною, починаючи з деякого номера. Наступний простий приклад показує, що це не так.
Приклад 3. Розглянемо геометричну прогресію
![]()
Оскільки в ній чергуються як додатні, так і від'ємні числа, то маємо при парному п
![]()
Тут п може
бути як завгодно великим. Тому, з якого б номера ми не починали, послідовність {![]() } не буде монотонною.
} не буде монотонною.
1.2. Монотонні підпослідовності
Повернемося до прикладу 3 в п. 1.1. Послідовність ![]()
![]()
не є монотонною, однак з неї можна здобути монотонні послідовності
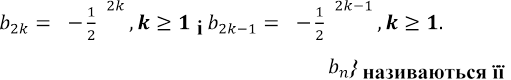 Подібні «частини» послідовності {
підлослідовностями.
Подібні «частини» послідовності {
підлослідовностями.
Означення 1. Нехай
{![]() } - послідовність дійсних чисел,
} - послідовність дійсних чисел,
{![]() }
— зростаюча послідовність натуральних чисел. Тоді послідовність називається
}
— зростаюча послідовність натуральних чисел. Тоді послідовність називається
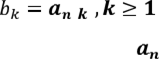 підпослідовністю послідовності
{ }
підпослідовністю послідовності
{ }
Так, у задачі 1 п. 1.1 послідовність {ап} містить монотонну
підпослідовність
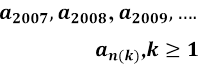 Її
можна подати у вигляді { } , де п(к) = к + 2006
.
Її
можна подати у вигляді { } , де п(к) = к + 2006
.
Усі розглянуті раніше послідовності або є монотонними, або містять монотонні підпослідовності. Простежимо цю закономірність на кількох прикладах. Приклад 1. Задамо послідовність рекурентним співвідношенням:
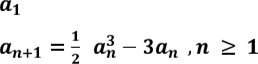 - довільне число з
інтервалу (-1; 0),
- довільне число з
інтервалу (-1; 0),
(2.1)
Зобразимо поведінку цієї послідовності графічно. Введемо
непарну функцію
![]() , х (-1; 1). Схематично
, х (-1; 1). Схематично
побудуємо її графік і на тому самому малюнку
проведемо пряму у = х, що дає змогу зобразити кілька членів даної
послідовності . Малюнок підказує, що підпослідовність ![]() зростає,
а
зростає,
а
 ,
,
> 0 ;
показати, що послідовність зростає.
Справді, оскільки члени ![]() мають
різні знаки і
мають
різні знаки і ![]() < 1, у
< 1, у
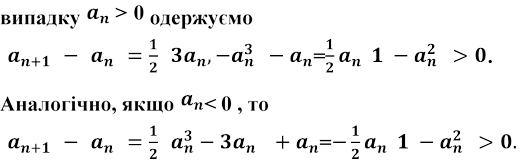
Отже, строгу монотонність обох підпослідовностей доведено.
Приклад 2. Покладемо
![]()
Очевидно, що ця послідовність не є монотонною.
Підпослідовності ![]() також не є монотонними.
також не є монотонними.
Більше того, виявляється, що для довільного рєN
підпослідовність ![]() (2.2) не є
монотонною.
(2.2) не є
монотонною.
Доведемо це
твердження методом від супротивного. Нехай для деякого ![]() підпослідовність
(2.2) монотонна. Візьмемо довільне непарне число l. Тоді якщо
підпослідовність
(2.2) монотонна. Візьмемо довільне непарне число l. Тоді якщо ![]()
![]() .
.
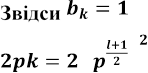 . У той самий час, при такому самому
. У той самий час, при такому самому ![]() число
число
не є повним квадратом, і отже, ![]() .
Послідовність
.
Послідовність ![]()
містить
нескінченно багато нулів і одиниць і не може бути монотонною. Одержали
суперечність з припущенням. Монотонну підпослідовність усе-таки виділити можна,
поклавши ![]() . Утім, не обов'язково для цього так
сильно
. Утім, не обов'язково для цього так
сильно
розріджувати
початкову послідовність. Відомо, що повні квадрати не можуть давати остачу 3
при діленні на 4. і тому підпослідовність ![]() також
монотонна.
також
монотонна.
Як бачимо, наші спроби сконструювати послідовність, що не містить монотонної підпослідовності, не увінчалися успіхом.
Причина в тому, що такої послідовності просто не існує. Теорема 1. Кожна послідовність містить монотонну підпослідовність.
Доведення
Нехай ![]() - довільна
послідовність. Починаючи з її першого
- довільна
послідовність. Починаючи з її першого
члена, будемо конструювати неспадну підпослідовність.
- найменший такий номер, що
-
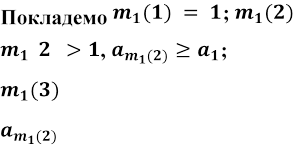 найменший
такий номер, що
найменший
такий номер, що ![]() і т.д. Якщо зазначена процедура не
обірветься, то так ми
і т.д. Якщо зазначена процедура не
обірветься, то так ми
побудуємо шукану
підпослідовність ![]() . Якщо ж процедура
обірветься, то
. Якщо ж процедура
обірветься, то
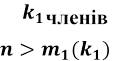
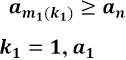 одержимо скінченну
неспадну послідовність із
одержимо скінченну
неспадну послідовність із ![]() причому при .
причому при .
(Зазначимо, що у випадку — найбільший член
початкової послідовності.)
Покладемо далі ![]() і, починаючи
з члена
і, починаючи
з члена
![]() , побудуємо
неспадну підпослідовність аналогічно до попереднього. Якщо процедура не
обривається, то отримано
, побудуємо
неспадну підпослідовність аналогічно до попереднього. Якщо процедура не
обривається, то отримано
шукану підпослідовність ![]() .
У протилежному
.
У протилежному
випадку маємо скінченну неспадну послідовність ![]() при
при ![]() .
Далі покладаємо
.
Далі покладаємо
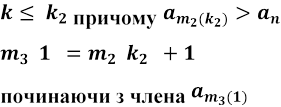 і знову
будуємо неспадну підпослідовність, і т.д. Є дві можливості:
і знову
будуємо неспадну підпослідовність, і т.д. Є дві можливості:
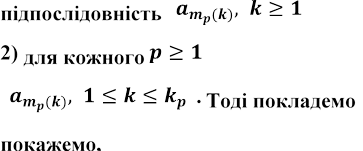 1) на деякому р-му кроці буде побудовано
нескінченну неспадну , яка і буде шуканою;
1) на деякому р-му кроці буде побудовано
нескінченну неспадну , яка і буде шуканою;
побудовано скінченну послідовність
![]() , і
, і
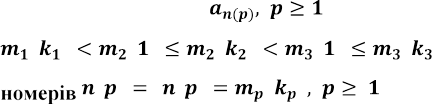 що
підпослідовність є шуканою. Справді,
що
підпослідовність є шуканою. Справді,
… і послідовність зростає. Отже, ![]() є
є
підпослідовністю. Крім того, за побудовою маємо
![]() … Таким чином,
… Таким чином, ![]() -
спадна
-
спадна
підпослідовність.
Теорема 1 є цікавим фактом, який можна покласти в основу теорії границь.
РОЗДІЛ II. ЕЛЕМЕНТАРНІ ВЛАСТИВОСТІ МОНОТОННИХ ФУНКЦІЙ
2.1. Означення та найпростіші приклади
У попередньому розділі розглядалися монотонні функції з дискретною областю визначення, а саме: вивчалися відображення, задані на скінченній множині або на множині всіх натуральних чисел. Перейдемо до функцій, визначених на довільній множині дійсних чисел.
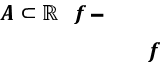
![]() Нехай , деяке
відображення з А в , В А .
Нехай , деяке
відображення з А в , В А .
Означення 1. Функція називається зростаючою (спадною) на множині В, якщо для кожної пари точок х1, х2 з В такої, що х1
< х2, справедлива нерівність
).
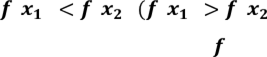 Означення 2. Функція
називається неспадною (незростаючою)
Означення 2. Функція
називається неспадною (незростаючою)
на В, якщо для кожної пари точок х1, х2 з В такої, що х1 < х2, справедлива нерівність
).
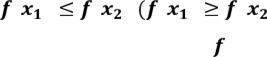 Означення 3. Функція
називається монотонною на В, якщо вона належить одному з перелічених вище
чотирьох типів.
Означення 3. Функція
називається монотонною на В, якщо вона належить одному з перелічених вище
чотирьох типів.
Функція ![]() називається строго монотонною на В,
якщо вона або зростає, або спадає на В.
називається строго монотонною на В,
якщо вона або зростає, або спадає на В.
Означення 4. Нехай
функція ![]() задовольняє одне з означень 1—3,
причому В = А. Тоді вона називається відповідно зростаючою (спадною
тощо) без вказування множини В.
задовольняє одне з означень 1—3,
причому В = А. Тоді вона називається відповідно зростаючою (спадною
тощо) без вказування множини В.
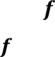 Означення
5. Нехай функція зростаюча (спадна), а функція g спадна (зростаюча),
то і g називаються строго монотонними різного типу. Якщо ж
Означення
5. Нехай функція зростаюча (спадна), а функція g спадна (зростаюча),
то і g називаються строго монотонними різного типу. Якщо ж ![]() зростаюча (спадна) і g зростаюча
(спадна), то
зростаюча (спадна) і g зростаюча
(спадна), то ![]() і g називаються
строго монотонними одного типу.
і g називаються
строго монотонними одного типу.
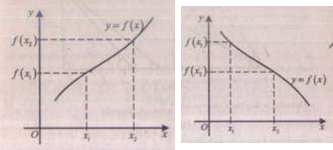
Геометрично
монотонність функції ![]() означає, що її графік
із збільшенням аргументу піднімається вгору (якщо
означає, що її графік
із збільшенням аргументу піднімається вгору (якщо ![]() зростаюча)
або опускається вниз (якщо
зростаюча)
або опускається вниз (якщо ![]() спадна). Типові
графіки наведені на малюнку.
спадна). Типові
графіки наведені на малюнку.
Приклад 1. Функція оберненої пропорційності
спадає на кожному з інтервалів 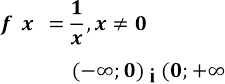 )
і не є монотонною на всій області визначення
)
і не є монотонною на всій області визначення ![]() ) .
) .
Розв'язання
Пояснимо тільки останнє твердження. Розглянемо три точки
![]()
Оскільки
![]() то не є неспадною на
то не є неспадною на ![]() \{0}.У той же
\{0}.У той же
час
![]() і не є незростаючою.
і не є незростаючою.
Цей приклад
застерігає від поширеної помилки. На перший погляд здається очевидним, що
монотонність функції ![]() на кожній з множин А
та В спричинює монотонність на їхньому об'єднанні. Однак це не завжди
правильно.
на кожній з множин А
та В спричинює монотонність на їхньому об'єднанні. Однак це не завжди
правильно.
Розглянемо складнішу функцію.
Приклад 2. Функція обчислення цілої частини дійсного числа
![]() є
неспадною і не є зростаючою. Розв'язання
є
неспадною і не є зростаючою. Розв'язання
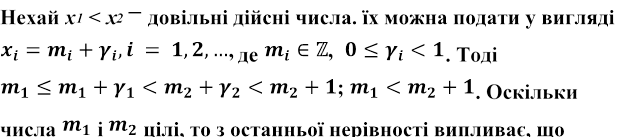
![]()
Отже, ![]() не
спадає.
не
спадає.
. Маємо:
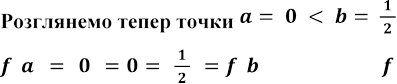 .
Виходить, не є зростаючою.
.
Виходить, не є зростаючою.
2.2. Монотонність породжує монотонність
Щоб розширити клас монотонних функцій, дослідимо, які операції зберігають цю властивість.
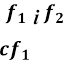 Теорема 1. Нехай
функції зростають (не спадають) на множині А. Тоді функції , де с
> 0,
Теорема 1. Нехай
функції зростають (не спадають) на множині А. Тоді функції , де с
> 0, ![]() зростають (не спадають) на А.
зростають (не спадають) на А.
Доведення
Обмежимося лише випадком строгої монотонності. Нехай х1![]() А,
А,
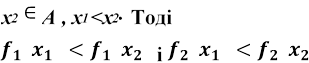 (1.1)
(1.1)
Помножимо першу нерівність на с > 0. Маємо ![]()
![]() , і функція
, і функція ![]() зростає на А. Додамо
нерівності (1.1), одержуємо:
зростає на А. Додамо
нерівності (1.1), одержуємо:
,
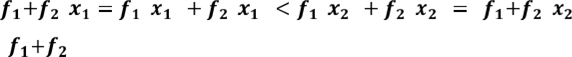 і
також зростає на А.
і
також зростає на А.
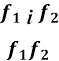 Теорема 2. Нехай
функції зростають і додатні на множині А. Тоді добуток також зростає
на А.
Теорема 2. Нехай
функції зростають і додатні на множині А. Тоді добуток також зростає
на А.
Доведення
Достатньо перемножити нерівності (1.1), утворені з додатних чисел.
Теорема 3. Нехай
функції ![]() додатні
на множині А,
додатні
на множині А, ![]() зростає на цій
множині, а
зростає на цій
множині, а ![]() спадає. Тоді частка
спадає. Тоді частка ![]() зростає на А.
зростає на А.
Доведення
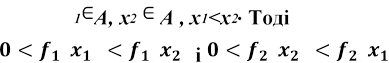 Нехай х
Нехай х
. З другої нерівності
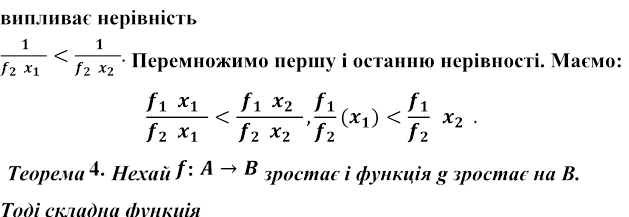
![]() також зростає.
також зростає.
Доведення
Нехай 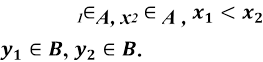 х . Тоді
х . Тоді ![]() ; Звідси
; Звідси
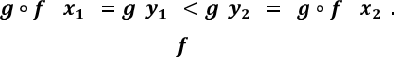 Теорема 5. Нехай
функція зростає (спадає). Тоді обернена функція
Теорема 5. Нехай
функція зростає (спадає). Тоді обернена функція ![]() існує і також зростає (спадає).
існує і також зростає (спадає).
Доведення
Обмежимося випадком зростання. Нехай - довільна фіксова-
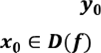 на точка з
на точка з ![]() . Існує така точка ,
що
. Існує така точка ,
що ![]() .
.
Жодна інша точка при відображенні ![]() у точку
у точку ![]() не
переходить, оскільки коли
не
переходить, оскільки коли
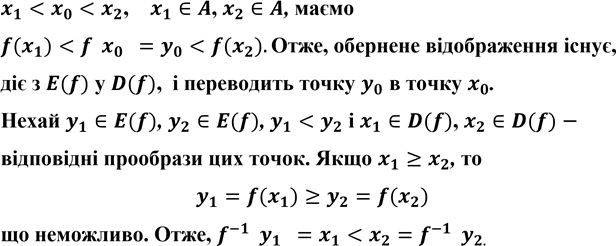
2.3. Інші приклади монотонних функцій
Застосуємо теореми 1-5 п. 2.2 для обгрунтування монотонності деяких елементарних функцій. Приклад 1. Лінійна функція
f(x) = kx + b, ![]() , де k, b — дійсні
параметри, зростає при к > 0 і спадає при к < 0.
, де k, b — дійсні
параметри, зростає при к > 0 і спадає при к < 0.
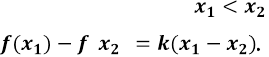 Доведемо це. Нехай .
Тоді
Доведемо це. Нехай .
Тоді
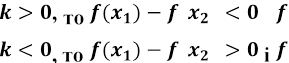 Якщо і
зростає.
Якщо і
зростає.
Якщо спадає.
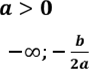 Приклад 2. Квадратична
функція f(x) = ax2 +bx + c,
Приклад 2. Квадратична
функція f(x) = ax2 +bx + c, ![]() ,
де a, b,c — дійсні параметри,
,
де a, b,c — дійсні параметри, ![]() ,
при спадає на
,
при спадає на
і зростає ![]() ; при
; при ![]() характер
характер
монотонності ![]() на
цих інтервалах змінюється на протилежний.
на
цих інтервалах змінюється на протилежний.
Обмежимося випадком ![]() . Виділяючи
повний квадрат,
. Виділяючи
повний квадрат,
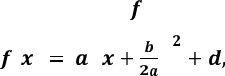 перетворимо до
вигляду
перетворимо до
вигляду
(3.1)
![]()
відповідно звуження на проміжки
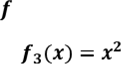
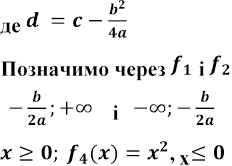
![]() .
Введемо також функції ,
.
Введемо також функції ,
З (3.1) випливають рівності
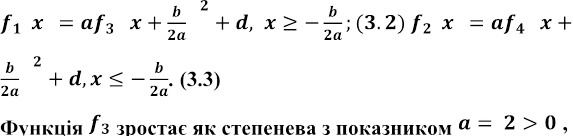
внутрішня лінійна
функція ![]() зростає , і за теоремою 4 п.2.2
складна функція
зростає , і за теоремою 4 п.2.2
складна функція
![]() також зростає. Згідно з теоремою 1 п.
також зростає. Згідно з теоремою 1 п.
2.2. остання
функція після множення на а > 0 залишається зростаючою. З рівності
(3.2) випливає тепер зростання ![]() .
.
Для функції ![]() міркування аналогічні й спираються на
(3.3). Варто врахувати тільки, що на відміну від
міркування аналогічні й спираються на
(3.3). Варто врахувати тільки, що на відміну від ![]() функція
функція
![]() спадає. Справді,
спадає. Справді,
, ,
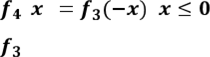
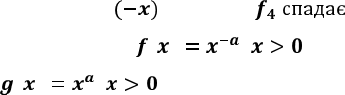 зростає, внутрішня лінійна функція спадає,
і . Приклад 3. При
зростає, внутрішня лінійна функція спадає,
і . Приклад 3. При ![]() степенева функція ,
, є
степенева функція ,
, є
спадною. Справді, функція , , додатна і зростає.
Функція ![]() і тому спадає.
і тому спадає.
Приклад 4. Зафіксуємо ![]() .
Функція
.
Функція ![]() зростає на
зростає на
проміжку
![]()
і спадає на проміжку
![]() .
.
Доведемо це.
Функція непарна і зростає на ![]()
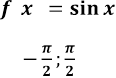 Вона зростає також на
Вона зростає також на
Функція ![]() періодична з періодом
періодична з періодом ![]() , і вона
, і вона
зростає на кожному проміжку виду
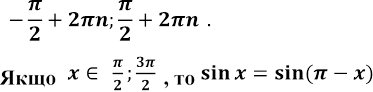 .
.
Тут внутрішня лінійна функція ![]() спадає,
спадає,
![]()
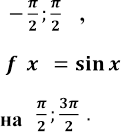 зростає на
зростає на ![]() і
спадає
і
спадає
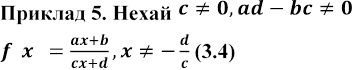 .
Дробово-лінійна функція
.
Дробово-лінійна функція
строго монотонна на кожному з інтервалів ![]() і
і
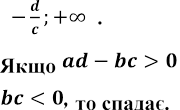 , то функція
, то функція ![]() на
них зростає, а коли
на
них зростає, а коли ![]()
Доведемо це. У чисельнику і знаменнику дробу (3.4) містяться многочлени. Поділивши їх у стовпчик, одержимо:
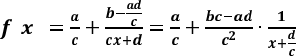 .
.
Введемо функцію оберненої пропорційності:
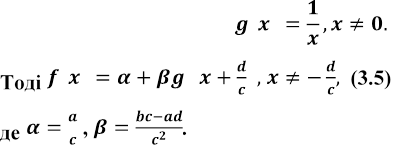
Внутрішня лінійна функція зростає, ![]() спадає
на кожному з
спадає
на кожному з
інтервалів ![]() .
Тому складна функція
.
Тому складна функція ![]() спадає на
спадає на
інтервалах ![]() З
рівності (3.5) робимо висновок,
З
рівності (3.5) робимо висновок,
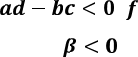 що при
що при ![]() ,
тобто коли , також спадає на кожному з цих інтервалів, а при ,
тобто коли
,
тобто коли , також спадає на кожному з цих інтервалів, а при ,
тобто коли ![]() ,
, ![]() на
них зростає.
на
них зростає.
2.4. Елементарне дослідження функцій на монотонність
Задача 1. Дослідити на монотонність функцію
![]() .
.
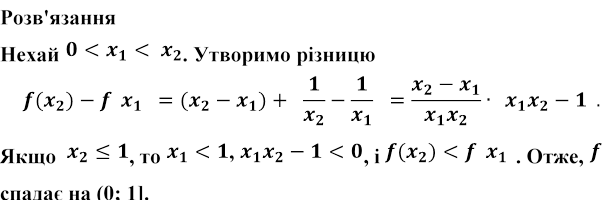
Якщо , то , , і , і зростає
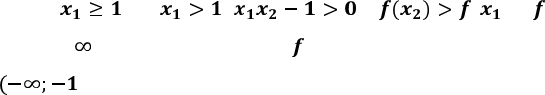 на [1; + ). Оскільки
функція непарна , вона зростає на
на [1; + ). Оскільки
функція непарна , вона зростає на
] і спадає на [—1; 0).
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір. Алгебра і початки аналізу. Профільний рівень. Підручник для 10 класу загальноосвітніх навчальних закладів. “Гімназія”, 2011. - С.70-72.
2. В. В. Зайцев, В. В. Рижков, М. І. Сканаві . Елементарна математика . Наука. Москва 1974. С. 228-238.
3. Р. А. Калнін. Алгебра і елементарні функції. Вища школа.
Київ 1969.С. 272-274.
4. Ф. П. Яремчук, П. А. Рудчєнко. Алгебра і елементарні функції. Наукова думка. Київ 1987.
3. П. І. Горнштейн, В. Б. Полонський, М. С. Якір. Задачі з параметрами. Тернопіль , “ Підручники і посібники ”, 2004. - С.187-189.
5. О. Кукуш. Монотонні послідовності і функції: Навчальний методичний посібник. г. “ Математика ”, №25-26, 2007. - С.4248, 82-83.
6. А. Єгоров, Ж. Раббот. Монотонні функції в конкурсних задачах [текст]: журнал “ Квант ”,2002. - №6. - С.34.
7. А. С. Истер. Решебник основных конкурсных задач по математике из сборника под редакцией М. И. Сканави. К. “ А. С. К. ”2002 - С.79.
8. Л. В. Лобанова, Л. П. Фінкельштейн. Вибрані задачі елементарної математики. Київ, “ Вища школа ”, 1989. - С.5.


про публікацію авторської розробки
Додати розробку
