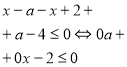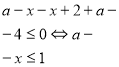Матеріал до проведення факультативних занять на тему "Графічне розв'язування рівнянь, нерівностей з двома змінними та їх систем"
Зміст
Вступ.................................................................................................................3-4.
І. Програма факультативного курсу з математики «Графічне розв’язування рівнянь, нерівностей з двома змінними та їх систем»
для учнів 10-11-х класів...................................................................................5-11.
ІІ. Графічне розв’язування рівнянь, нерівностей з двома змінними та їх систем...............................................................................................................12-47.
1. Лінійні рівняння та нерівності з двома змінними..........................12-15.
2. Системи лінійних рівнянь з двома невідомими............................16-20.
3. Системи лінійних нерівностей та рівнянь з двома невідомими...21-25.
4. Квадратні рівняння та нерівності з двома невідомими.................26-27.
5. Геометрична інтерпретація розв’язків нерівності з двома
невідомими............................................................................................28-33.
6. Взаємозв’язок теорії з практикою в процесі вивчення
математики...........................................................................................34-36.
7. Графічні методи розв’язування рівнянь та нерівностей з параметрами...................................................................................................37-44.
8. Математичне мистецтво Моріца Ешера.........................................45-47.
9.Висновки..............................................................................................48.
10. Список використаної літератури...................................................49-50
ВСТУП
«Глибоке вивчення природи є найплодотворнішим джерелом математичних відкриттів. Це вивчення, висуваючи певну мету дослідження, має не тільки ту перевагу, що виключає незрозумілі питання і непотрібні обчислення, але воно також є правильним засобом формування самого аналізу й розкриття в ньому тих елементів, знати які дуже важливо і які наука повинна завжди зберігати. Ці основні елементи є тими, що повторюються у всіх явищах природи».
Ж.Фур'є
Починаючи з сьомого класу в центрі уваги шкільної математики знаходиться поняття функції, її графіка. Але об'єм шкільного підручника не дозволяє показати різноманітність задач, їх красу ї глибину математичних знань, необхідних для їх розв'язання, а також прикладне застосування.
Навчально-методичний посібник складається з восьми розділів, які містять теоретичний і практичний матеріал по графічному розв'язуванні рівнянь, нерівностей та їх систем.
Високого рівня розвитку досягла сучасна математика. Таким чином в даній розробці показано розвиток ідеї від розв'язування нескладних рівнянь і нерівностей до задач прикладного характеру.
Математика виникла із задач. Основну роль, звичайно, відіграють задачі, поставлені життям. Вони змушують розробляти нові алгоритми, розкривати нові закономірності, створювати нові методи дослідження, тобто збагачувати математику новими відкриттями.
Особливо корисними є математичні задачі для виявлення творчої думки учнів. Саме із задач починається зацікавленість багатьох учнів математикою. Ось чому більша частина наукової роботи присвячена задачам.
Цей матеріал може використовуватися на факультативних заняттях, гуртковій роботі при поглибленому вивченні математики.
Програма
факультативного курсу з математики «Графічне розв’язування рівнянь, нерівностей з двома змінними та їх систем» для учнів 10-11-х класів.
Пояснювальна записка
Факультативне навчання математики має на меті поглиблювати знання учнів, здобуті при вивченні шкільного курсу математики.
Основна мета даного факультативного курсу- розширення й поглиблення відомостей окремих тем курсу алгебри, завдання яких пропонуються при вступі у вищі навчальні заклади. Розв’язання таких завдань без певної підготовки викликає труднощі в учнів, тому виникає потреба у створенні такої навчальної програми яка б дала можливість розглянути завдання підвищеної складності, де застосовуються нестандартні методи розв’язування рівнянь, нерівностей та їх систем.
Математика- один із опорних предметів середньої школи, який забезпечує успішне вивчення інших дисциплін, насамперед, предметів природничо-математичного циклу.
Основним завданням шкільного курсу математики є інтелектуальний розвиток учнів (розвиток логічного мислення, просторової уяви, алгоритмічної та графічної культури, пам’яті, уваги і тд.).
Факультативний курс математики має на меті сприяти досягненню учнями високого рівня математичної підготовки, розвитку стійких пізнавальних математичних інтересів.
Програму структуровано за темами загального курсу математики загальноосвітньої школи, для кожної теми визначено орієнтовну кількість навчальних годин,основну мету, основні вимоги до результатів навчання. Кожну тему підкріплено задачами, методи яких укладаються в традиційну програму шкільного курсу математики.
В програмі підвищено рівень вивчення рівнянь, нерівностей з двома невідомими та їх систем.
Вчитель може сам обирати оптимальну форму навчання. Це залежить від особливостей учнів та змісту навчального матеріалу.
Головна мета полягає у найповнішій реалізації можливостей учнів, розвитку їх творчого потенціалу та індивідуальних здібностей.
Програма розрахована на один рік навчання.
Теми, запропоновані в програмі, є орієнтовними. Вчитель може самостійно добирати додаткові теми та завдання залежно від їх актуальності, не порушуючи при цьому логічної побудови факультативного курсу.
Навчальні заняття по даній програмі передбачають застосування традиційних та нетрадиційних форм і методів навчання: лекцї, семінари, дискусії, конференції, ділові ігри тд,.
Заняття можуть бути відкритими для інших школярів. Це дасть змогу підвищити інтерес до вивчення математики. Певним внеском в оновлення форм навчання мають стати комп’ютерні засоби навчання.
Зміст
1. Лінійні рівняння та нерівності з двома невідомими (2 години)
Розв’язування рівнянь виду![]() .
.
Розв’язування нерівностей виду![]()
![]() ;
;
![]()
![]()
Основна мета:
- розширити знання про лінійні рівняння та нерівності, методи їх розвязування.
Основні вимоги:
- знати типи лінійних рівнянь і нерівностей;
- уміти розв’язувати дані рівняння та нерівності аналітично і графічно;
- розв’язувати окремі випадки таких рівнянь і нерівностей, коли в них одне з невідомих відсутнє.
2. Системи лінійних рівнянь з двома невідомими (4 години)
Розв’язування систем виду 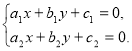
Системи алгебраїчних рівнянь, що розв’язуються методом підстановки, методом додавання. Розв’язування систем алгебраїчних рівнянь за допомогою визначників.
Основна мета:
- розширити знання про різні типи систем лінійних рівнянь з двома невідомими та методи їх розв’язування.
Основні вимоги:
- знати типи систем лінійних рівнянь з двома невідомими;
- уміти розв’язувати системи лінійних рівнянь з двома невідомими способом підстановки, способом додавання, за допомогою визначників;
- розв’язувати системи лінійних рівнянь аналітично і графічно;
- уміти розв’язувати системи лінійних рівнянь з двома невідомими, коли кількість рівнянь перевищує кількість невідомих.
3. Системи лінійних нерівностей та рівнянь з двома невідомими (6 годин)
Системи нерівностей типу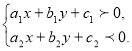 .
.
Нестандартні системи.
Основна мета:
-систематизувати відомості про системи нерівностей даного виду та методи їх розв’язуваня.
Основні вимоги:
- знати типи систем лінійних нерівностей;
-уміти розвязувати дані системи аналітично і графічно.
4. Квадратні рівняння та нерівності з двома невідомими (4 години)
Квадратні рівняння виду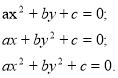
Квадратні нерівності типу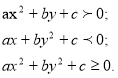
Методи розв’язування даних рівнянь та нерівностей.
Основна мета:
- систематизувати типи квадратних рівнянь та нерівностей з двома невідомими та методи їх розв’язування.
Основні вимоги:
- уміти знайти таку множину пар чисел, яка б задовольняла дане рівняння або нерівність;
- побудувати геометрично всю множину розв’язків таких рівнянь та нерівностей.
5. Геометрична інтерпретація розв’язків нерівності з двома невідомими (8 годин)
Криві другого порядку на площині, задані рівнянням ![]() . Множина точок, що задовольняють нерівність
. Множина точок, що задовольняють нерівність ![]() та
та ![]() .
.
Основна мета:
- узагальнити та ситематизувати знання по побудові графіків рівнянь та нерівностей з двома змінними.
Основні вимоги:
- уміти будувати графіки нерівностей з двома змінними різних типів;
- за графіками нерівностей записувати дані нерівності.
6. Взаємозв’язок теорії з практикою в процесі вивчення математики (4 години)
Задачі прикладного змісту, які розв’язуються за допомогою систем нерівностей з двома невідомими.
Основна мета:
- показати приклади розв’язування задач прикладного характеру за допомогою систем нерівностей з двома невідомими.
Основні вимоги:
- знати розв’язувати дані задачі аналітично;
- уміти подати геометричну інтерпретацію розв’язків задач прикладного змісту;
- подавати геометрично зображені множини за допомогою явних нерівностей з двома невідомими.
7. Графічні методи розв’язування рівнянь і нерівностей з параметрами
(5 годин)
Розв’язування рівнянь і нерівностей з двома невідомими, які містять параметри. Комбінування різних методів при розв’язуванні даних рівнянь і нерівностей. Нестандартні типи рівнянь і нерівностей з параметрами.
Основна мета:
- узагальнити та систематизувати весь матеріал по розвֹязуванні різних типів рівнянь, нерівностей та їх систем.
Основні вимоги:
- знати графічні методи розв’язування рівнянь та нерівностей з параметрами;
- вміти поєднувати різні методи при розв’язувані нестандартних систем рівнянь і нерівностей з параметрами.
8. Математичне мистецтво Моріца Ешера (2 години)
Взаємозв’язок творів Моріца Ешера з геометричною інтерпретацією розв’язків певного типу рівнянь і нерівностей та їх систем з декількома невідомими.
Основна мета:
- встановити, чи можна за допомогою геометричної інтерпритації розв’язків рівнянь, нерівностей та їх систем з декількома невідомими побудувати малюнок, який би мав не тільки математичний зміст.
Основні вимоги:
- зобразити на площині геометричну інтерпритацію розв’язків рівнянь чи нерівностей, які забезпечували б розвиток просторової уяви, логічного мислення, філософського тлумачення буття, нескінченість простору, невичерпні можливості людського розуму та фантазії, які засвідчують найвищу досконалість застосування вивченого.
ІІ. Графічне розв’язування рівнянь, нерівностей з двома змінними та їх систем
1. Лінійні рівняння та нерівності з двома невідомими
Розв’язати рівняння ax+by+c=0 або нерівність ax+by+c>0 означає знайти таку множину E={(x, y)} пар чисел (х, у), кожний елемент якої задовольняє рівняння або нерівність.
Приклади
Розв’язати рівняння.
1. 3х-2у-12=0.
Розв’яжемо це рівняння відносно у: ![]() .
.
Множина ![]() розв’язків даного рівняння описується умовами:
розв’язків даного рівняння описується умовами: ![]() ,
, ![]() .
.
Наприклад: х=0, ![]() ; х=1,
; х=1, ![]() ,… і т. д., тобто
,… і т. д., тобто ![]() і є нескінченною. Можна було б взяти:
і є нескінченною. Можна було б взяти: ![]() ,
, ![]() . Надаючи значень у та підставляючи їх у формулу
. Надаючи значень у та підставляючи їх у формулу ![]() , дістали б ту саму множину
, дістали б ту саму множину ![]() .
.
Геометрично ця множина зображується множиною точок графіка ![]() (рис. 1).
(рис. 1).
2. ![]() .
.
Розв’яжемо цю нерівність відносно у: ![]() . Взявши х=2, дістанемо
. Взявши х=2, дістанемо ![]() ; при
; при ![]() (що якраз менше за
(що якраз менше за ![]() ) матимемо пару (2,
) матимемо пару (2, ![]() ), яка задовольняє дану нерівність. Беручи інші х, таких пар, як видно, можна набрати безліч Е={(2,
), яка задовольняє дану нерівність. Беручи інші х, таких пар, як видно, можна набрати безліч Е={(2, ![]() ), (4,
), (4, ![]() ), …}.
), …}.
Для геометричного зображення множини Е розв’язків нерівності будуємо графік 3х-2у-12=0, тобто пряму лінію.
Оскільки ![]() , то множина Е розташована на півплощині, що знаходиться нижче прямої 3х-2у-12=0 ( або
, то множина Е розташована на півплощині, що знаходиться нижче прямої 3х-2у-12=0 ( або ![]() ).
).
Слід зауважити, що нерівність 3х-2у-12<0 або ![]() має множину Е розв’язків, яка розташована вище прямої 3х-2у=0 (або
має множину Е розв’язків, яка розташована вище прямої 3х-2у=0 (або ![]() ). Наприклад, (2, -2), (3, -1) належать цій множині.
). Наприклад, (2, -2), (3, -1) належать цій множині.
Розглянемо приклади окремих випадків таких рівнянь та нерівностей, коли в них одне з невідомих відсутнє.
3. Знайти кілька елементів множини Е розв’язків геометрично: а)![]() ; б)
; б)![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Розв’язання![]()
а) ![]() . Це означає, що множина
. Це означає, що множина ![]() складається з пар, у яких завжди
складається з пар, у яких завжди ![]() , а
, а ![]() - довільне дійсне число. Наприклад:
- довільне дійсне число. Наприклад: ![]()
![]()
![]() ,
, ![]() 0)
0) ![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() і т. д. Геометрично множина
і т. д. Геометрично множина ![]() є пряма, паралельна осі
є пряма, паралельна осі ![]() і розташована вліво від неї на відстані в
і розташована вліво від неї на відстані в ![]() масштабних одиниць (рис. 2).
масштабних одиниць (рис. 2).
б) ![]() . Множина
. Множина ![]() розв’язків цієї нерівності складається з пар, у яких
розв’язків цієї нерівності складається з пар, у яких ![]() , а
, а ![]() довільне дійсне число. Наприклад, (-2, 2), (-1, 3)
довільне дійсне число. Наприклад, (-2, 2), (-1, 3) ![]() . Геометрично множина
. Геометрично множина ![]() є півплощиною, яка розташована вправо від прямої
є півплощиною, яка розташована вправо від прямої ![]() (рис.. 2).
(рис.. 2).
в)![]() . Маємо:
. Маємо: ![]() ,
, ![]() - довільне:
- довільне: ![]() (рис. 3).
(рис. 3).
г) ![]() . Маємо:
. Маємо: ![]() ,
, ![]() - довільне: (2, 3)
- довільне: (2, 3) ![]() , (1, 0)
, (1, 0) ![]() і т. п. (рис. 3).
і т. п. (рис. 3).
Вправи
-
На площині побудувати множину точок
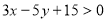 . Чи належать точки (1, -2), (0, 3), (-6, 0) цій множині?
. Чи належать точки (1, -2), (0, 3), (-6, 0) цій множині?
- Написати множину точок площини, які: а) віддалені від осі ОХ на віддаль, більшу трьох масштабних одиниць; б) від осі ОУ на віддаль, меншу двох масштабних одиниць. (рис. 3).
-
Якій із множин :
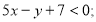
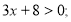
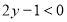 належить елемент (1, 15)? Установити це аналітично та графічно.
належить елемент (1, 15)? Установити це аналітично та графічно.
-
Серед пар чисел (-2, 1), (0, 3), (1, -3) знайти таку, яка належить : а) одній із множин; б) кожній із множин:
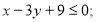
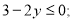
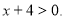
2. Системи лінійних рівнянь з двома невідомими
Розв’язком системи двох або більшого числа лінійних рівнянь з двома невідомими є така множина ![]() пар чисел ,які задовольняють одночасно кожне рівняння системи. Тому, коли
пар чисел ,які задовольняють одночасно кожне рівняння системи. Тому, коли ![]() і т. д. є множиною розв’язків системи.
і т. д. є множиною розв’язків системи.
Приклади
- Знайти множини розв’язків таких систем та подати геометричне зображення розв’язків:
а) ![]() б)
б) ![]() в)
в) 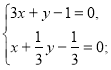 г)
г) 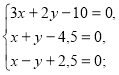 д)
д) 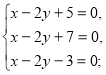 е)
е) 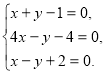
Розв’язання
а)Помноживши друге рівняння на -2 та додавши обидва рівняння, дістанемо:![]() далі
далі ![]()
![]() (рис. 4).
(рис. 4).
Маємо ![]() .
.
Геометрично це означає, що графіки (прямої лінії) відповідних рівнянь систем мають одну спільну точку, а саме: ![]() (рис. 4):
(рис. 4): ![]() .
.
б) Тут маємо вивідне рівняння ![]() , або
, або ![]() і
і ![]() (або
(або ![]() ) не існує. Множиною
) не існує. Множиною ![]() розв’язків системи є порожня множина
розв’язків системи є порожня множина ![]() . Геометрично це означає, що графіки (прямі лінії) відповідних рівнянь системи не мають жодної спільної точки (рис. 5):
. Геометрично це означає, що графіки (прямі лінії) відповідних рівнянь системи не мають жодної спільної точки (рис. 5): ![]() .
.
в) Вивідне рівняння має вигляд ![]() або
або ![]() . А це означає, що система задовольняється нескінченною множиною пар дійсних чисел
. А це означає, що система задовольняється нескінченною множиною пар дійсних чисел ![]() та
та ![]() , які задовольняють або перше, або друге рівняння; множина
, які задовольняють або перше, або друге рівняння; множина ![]() - нескінченна. Геометрично це означає, що графіки (прямі лінії) відповідних рівнянь системи мають безліч спільних точок, прямі зливаються (рис. 6):
- нескінченна. Геометрично це означає, що графіки (прямі лінії) відповідних рівнянь системи мають безліч спільних точок, прямі зливаються (рис. 6): ![]()
![]()
Тепер дістанемо розв’язки цих систем за допомогою визначників а) 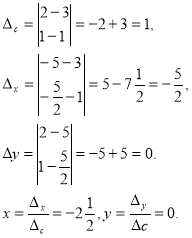
Відповідь: ![]() .
.
б)![]()
![]()
Відповідь:![]() .
.
![]() в)
в) 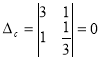 ,
, ![]() .
.
Відповідь. Система має нескінченну множину ![]() розв’язків, яка знаходиться з умови:
розв’язків, яка знаходиться з умови: ![]() ,
, ![]() .
. ![]()
(рис. 6).
г) Зводимо розв’язання цієї системи до розв’язання системи двох рівнянь з двома невідомими (адже тут кількість рівнянь перевищує кількість невідомих).
Множина ![]() розв’язків даної системи повинна задовольняти кожну систему:
розв’язків даної системи повинна задовольняти кожну систему:
![]()
![]()
![]()
Виберемо ту з них, визначник якої ![]() . Нехай візьмемо першу, з якої знаходимо
. Нехай візьмемо першу, з якої знаходимо ![]() ,
, ![]() , тобто
, тобто ![]() .
.
Перевіримо, чи буде множина ![]() розв’язком другої та третьої систем. Для цього досить перевірити рівняння
розв’язком другої та третьої систем. Для цього досить перевірити рівняння ![]() :
:
![]() ,
,![]() .
.
Відповідь: ![]() (рис. 7).
(рис. 7).
д) Маємо:
![]()
![]()
![]()
Тут визначник кожної системи ![]() Виберемо тоді ту систему, в якій
Виберемо тоді ту систему, в якій ![]() або
або ![]() . Візьмемо, наприклад, першу
. Візьмемо, наприклад, першу ![]() . Система розв’язків не має,
. Система розв’язків не має, ![]()
![]() . Геометрично: три прямі лінії, побудовані з рівнянь системи, різні і паралельні (рис. 8):
. Геометрично: три прямі лінії, побудовані з рівнянь системи, різні і паралельні (рис. 8): ![]() .
.
е) Маємо:
![]()
![]()
![]()
(рис. 8).
Розглядаємо першу систему:
![]()
![]()
![]()
![]()
![]()
Маємо: ![]() .
.
Перевіримо третє рівняння даної системи: ![]()
![]() .
.
Висновок та відповідь: дана система розв’язку не має, ![]() .
.
Геометрично: три прямі лінії, побудовані відповідно за рівняннями системи, різні і не мають жодної спільної точки (рис. 9): ![]() .
.
Вправи
- Для системи написати множини розв’язків та зобразити їх геометрично:
а) 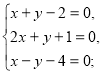 в)
в) 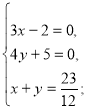 б)
б) 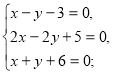 г)
г) 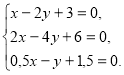
- Встановити аналітично та графічно, чи належить пара (1, 2) множині розв’язків системи:
а) 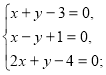 б)
б) 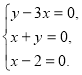
3. Скласти систему чотирьох лінійних рівнянь з двома невідомими, щоб пара (2, -3) належала до множини розв’язків цієї системи.
- Системи лінійних нерівностей та рівнянь з двома невідомими
Раніше мова йшла про розв’язування нерівностей з двома невідомими першого степеня. Розв’язати систему кількох лінійних нерівностей з двома невідомими означає знайти таку множину ![]() пар чисел, які задовольняють кожну нерівність. Якщо
пар чисел, які задовольняють кожну нерівність. Якщо![]() і т. д. множини розв’язків кожної нерівності, то
і т. д. множини розв’язків кожної нерівності, то ![]() і т.д. є множина розв’язків системи. Геометрично множина
і т.д. є множина розв’язків системи. Геометрично множина ![]() є спільною частиною (перетин) всіх тих півплощин, які визначають кожну нерівність системи.
є спільною частиною (перетин) всіх тих півплощин, які визначають кожну нерівність системи.
Приклади
Зобразити геометрично множину ![]() розв’язків системи та записати
розв’язків системи та записати ![]() в явному вигляді за допомогою нерівностей:
в явному вигляді за допомогою нерівностей:
а) ![]()
![]() б)
б) ![]() в)
в)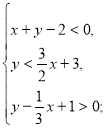 г)
г)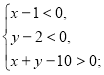 д)
д) 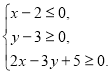
Розв’язання
а) І. Розв’яжемо обидві нерівності відносно ![]() :
:
![]()
![]() .
.
Будуємо графіки:
![]()
![]()
![]() .
.
Множиною ![]() є та частина площини, яка знаходиться одночасно вище прямої
є та частина площини, яка знаходиться одночасно вище прямої ![]() та нижче прямої
та нижче прямої ![]() (рис. 10).
(рис. 10).
ІІ. Знаходимо точку перетину прямих, для чого розв’яжемо систему 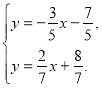 Маємо:
Маємо: ![]() . Множина
. Множина ![]() залишається системою:
залишається системою: 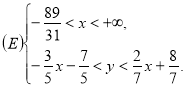
(рис. 10).
Покажемо, як цю систему можна одержати інакше. За умовою ![]()
![]() , звідси
, звідси ![]() . Із останньої нерівності випливає:
. Із останньої нерівності випливає: ![]() , або
, або ![]() . Тому шукана система, що явно описує множину
. Тому шукана система, що явно описує множину ![]() , має вигляд:
, має вигляд: 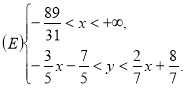
Конкретний приклад. Нехай ![]() , що становить більше
, що становить більше ![]() . Тоді
. Тоді ![]() . Це означає, що множина
. Це означає, що множина ![]() має в своєму складі пари (1, -1), (1, 0), (1, 1) і т. д., а пари (1, 2), (1, -2) і т. д. не належать до
має в своєму складі пари (1, -1), (1, 0), (1, 1) і т. д., а пари (1, 2), (1, -2) і т. д. не належать до ![]() .
.
Множину ![]() можна записати як
можна записати як ![]() , тобто
, тобто ![]() (див. рис. 10), де
(див. рис. 10), де 
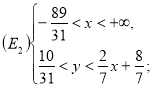
або 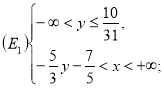
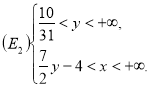
б) І. Розв’яжемо обидві нерівності відносно ![]() :
: ![]() ,
, ![]() . Будуємо графіки:
. Будуємо графіки: ![]() ,
, ![]() . Множина
. Множина ![]() ; півплощини, що відповідають кожній нерівності системи, не мають жодної спільної точки (рис. 11).
; півплощини, що відповідають кожній нерівності системи, не мають жодної спільної точки (рис. 11).
ІІ. Із того що ![]() та
та ![]() випливає:
випливає: ![]() , звідки
, звідки ![]() ,
, ![]() , що неможливо. Отже, дана система розв’язків не має,
, що неможливо. Отже, дана система розв’язків не має, ![]() .
.
в) І. Розв’яжемо кожну нерівність відносно ![]() :
: ![]() ,
, ![]() ,
, ![]() . Будуємо графіки:
. Будуємо графіки: ![]() ,
, ![]() ,
, ![]() . Знаходимо, що множина
. Знаходимо, що множина ![]() розв’язків даної системи зображується тими точками площини, які лежать всередині трикутника
розв’язків даної системи зображується тими точками площини, які лежать всередині трикутника ![]() , причому, точки сторін його не належать множині
, причому, точки сторін його не належать множині ![]() (рис. 12).
(рис. 12).
ІІ. Знаходимо координати точок ![]() перетину відповідних прямих:
перетину відповідних прямих:
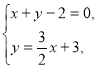
![]()
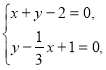
![]()
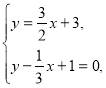
![]() .
.
Множина ![]() є об’єднанням множин
є об’єднанням множин ![]() та
та ![]() , які представлені внутрішніми точками
, які представлені внутрішніми точками ![]() і
і ![]()
![]() і записується:
і записується: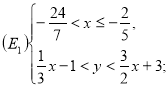
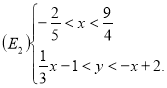
(рис. 12)
Якщо провести ![]() , то
, то ![]() , де
, де ![]() та
та ![]() є внутрішні точки відповідно
є внутрішні точки відповідно ![]() та
та ![]() :
:
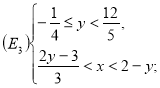
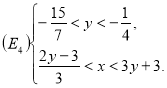
г) І. Тут маємо: ![]() ,
, ![]() ,
, ![]() . Будуємо графіки:
. Будуємо графіки: ![]() ,
, ![]() ,
, ![]() . Множина
. Множина ![]() повинна бути одночасно зліва від прямої
повинна бути одночасно зліва від прямої ![]() , нижче прямої
, нижче прямої ![]() та вище прямої
та вище прямої ![]() . Неважко помітити, що
. Неважко помітити, що ![]()
(рис. 13).
ІІ. За умовою ![]() , звідки
, звідки ![]() , або
, або ![]() . Але ж за тією самою умовою
. Але ж за тією самою умовою ![]() . Цього не може бути, система немає розв’язку, тобто
. Цього не може бути, система немає розв’язку, тобто ![]() .
.
д) Знаходимо :![]() ,
, ![]() ,
, ![]() .
.
Побудувавши графіки: ![]() ,
, ![]() ,
, ![]() , знайдемо, що множина
, знайдемо, що множина ![]() складається з одного елемента:
складається з одного елемента: ![]() . Підставивши
. Підставивши ![]() в третю нерівність, впевнюємось у тому, що
в третю нерівність, впевнюємось у тому, що ![]() є розв’язком даної системи (рис. 14).
є розв’язком даної системи (рис. 14).
- Квадратні рівняння та нерівності з двома невідомими
Розглянемо деякі випадки квадратних рівнянь та нерівностей з двома невідомими: ![]() ,
, ![]() , і т. п.,
, і т. п., ![]() ,
, ![]() тощо.
тощо.
Розв’язати таке рівняння або нерівність означає знайти таку множину ![]() пар чисел, яка б задовольняла це рівняння або нерівність.
пар чисел, яка б задовольняла це рівняння або нерівність.
Приклади
Знайти кілька розв’язків, якщо вони є, та побудувати геометрично всю множину розв’язків таких рівнянь та нерівностей:
а) ![]() ; б)
; б) ![]() ;
;
а`) ![]() ; б`)
; б`) ![]() ;
;
Розв’язання
а) Розв’яжемо рівняння відносно ![]() :
: ![]() . Надаючи
. Надаючи ![]() будь яких дійсних значень, будемо одержувати відповідні значення
будь яких дійсних значень, будемо одержувати відповідні значення ![]() . Так
. Так ![]() ,
, ![]() . Будуємо графік
. Будуємо графік ![]()
(рис. 15).
Геометрично вся множина ![]() розв’язків цього рівняння збігається з множиною точок параболи
розв’язків цього рівняння збігається з множиною точок параболи ![]() .
.
а`) Маємо ![]() . Надаючи
. Надаючи ![]() будь-яких значень, і беручи
будь-яких значень, і беручи ![]() більшим за
більшим за ![]() , дістанемо пари розв’язків цієї нерівності. Так,
, дістанемо пари розв’язків цієї нерівності. Так, ![]() ,
, ![]() .
.
Геометрично це та частина площини (див.рис. 15), яка розташована вище параболи ![]() . Друга частина площини (заштрихована горизонтальними лініями) виражає множину розв’язків нерівності
. Друга частина площини (заштрихована горизонтальними лініями) виражає множину розв’язків нерівності ![]() .
.
б) Маємо ![]() ,
, ![]() . Тут
. Тут ![]() можна надавати не будь-яких значень, а тільки ті, які задовольняють нерівність
можна надавати не будь-яких значень, а тільки ті, які задовольняють нерівність ![]() , або
, або ![]() , тобто
, тобто ![]() .
.
Наприклад, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(рис. 16).
Геометрично вся множина ![]() є множиною точок кола:
є множиною точок кола: ![]() ,
, ![]() (рис. 16).
(рис. 16).
б`) Тут маємо ![]() ,
, ![]() ,
, ![]() . Якщо надати
. Якщо надати ![]() значень із відрізка
значень із відрізка ![]() та брати
та брати ![]() таким, щоб
таким, щоб ![]() , то дістанемо пари розв’язків цієї нерівності:
, то дістанемо пари розв’язків цієї нерівності: ![]() ,
, ![]() тощо.
тощо.
Геометрично вся множина ![]() розв’язків цієї нерівності є множиною точок площини, розташованих в середині кола
розв’язків цієї нерівності є множиною точок площини, розташованих в середині кола ![]() . Множина точок, розташованих поза колом, геометрично виражає множину розв’язків нерівності
. Множина точок, розташованих поза колом, геометрично виражає множину розв’язків нерівності ![]() (рис. 16).
(рис. 16).
- Геометрична інтерпретація розв’язків нерівності
з двома невідомими
Для відповіді на запитання нагадаємо, що кожна крива другого порядку на площині, задана рівнянням ![]() , розбиває всі точки площини на три множини: а) точки що належать кривій, їх координати задовольняють рівняння
, розбиває всі точки площини на три множини: а) точки що належать кривій, їх координати задовольняють рівняння ![]() ; б) точки що знаходяться «над» кривою, їх координати задовольняють нерівність
; б) точки що знаходяться «над» кривою, їх координати задовольняють нерівність ![]() ; в) точки, що знаходяться «під» кривою, їх координати задовольняють нерівність
; в) точки, що знаходяться «під» кривою, їх координати задовольняють нерівність ![]() .
.
Приклади
-
Побудувати графік нерівності
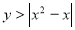 .
.
Розв’язання. Побудуємо спочатку графік функції ![]() , потім графік функції
, потім графік функції ![]() (рис. 17). Розв’язком нерівності, а отже, її графіком, є заштрихована частина площини (рис. 17).
(рис. 17). Розв’язком нерівності, а отже, її графіком, є заштрихована частина площини (рис. 17).
-
Побудувати графік нерівності
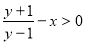 .
.
Розв’язання.
Якщо ![]() , то
, то ![]() ;
; ![]() .
.
Розглянемо три випадки:
а) ![]() , тоді
, тоді ![]() ;
;
б) ![]() , тоді
, тоді ![]() ;
;
в) ![]() , тоді
, тоді ![]() ;
;
Якщо ![]() , то
, то ![]() ;
; ![]() .
.
Знову розглянемо три випадки:
а) ![]() , тоді
, тоді ![]() ;
;
б) ![]() , тоді
, тоді ![]() ;
;
в) ![]() , тоді
, тоді ![]() ,
,
(рис. 17)
(рис. 18)
Будуємо графік функції ![]() (рис. 18). Заштрихована частина площини і буде графіком даної нерівності.
(рис. 18). Заштрихована частина площини і буде графіком даної нерівності.
Зведення нерівності до виду ![]() не завжди вдається.
не завжди вдається.
Наприклад.
-
Побудувати графік нерівності
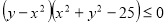 . Розв’язання. Розглянемо дві системи нерівностей:
. Розв’язання. Розглянемо дві системи нерівностей:
а) 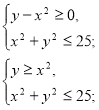 б)
б) 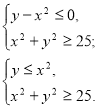
Зрозуміло, що графіком нерівності ![]() є точки площини, які лежать всередині або поза колом
є точки площини, які лежать всередині або поза колом ![]() . Враховуючи нерівності
. Враховуючи нерівності ![]() для першої і
для першої і ![]() для другої системи, будуємо графік вихідної нерівності (рис. 19).
для другої системи, будуємо графік вихідної нерівності (рис. 19).
Зауваження. Аналогічно можна було б розв’язати і приклад ![]()
![]() .
.
Зведемо до спільного знаменника в лівій частині: ![]() .
.
Розглянемо дві системи нерівностей:
а) ![]() б)
б) ![]() і т. д.
і т. д.
Розв’язуючи приклад ![]() першим способом, ми по суті застосовували метод інтервалів (для
першим способом, ми по суті застосовували метод інтервалів (для ![]() і
і ![]() ). Використаємо цей метод для розв’язування нерівностей, коли змінні знаходяться під знаком модуля.
). Використаємо цей метод для розв’язування нерівностей, коли змінні знаходяться під знаком модуля.
(рис. 19)
(рис. 20)
-
Побудувати графік нерівності
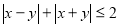 .
.
Розв’язання. Знайдемо нулі функції ![]() , або
, або ![]() ;
; ![]() , або
, або ![]() . Ці дві прямі розбивають площину на чотири області (які відіграють роль інтервалів). У кожній з цих областей беремо контрольну точку і визначаємо знаки підмодульних виразів.
. Ці дві прямі розбивають площину на чотири області (які відіграють роль інтервалів). У кожній з цих областей беремо контрольну точку і визначаємо знаки підмодульних виразів.
а) Для першої області ![]() ,
, ![]() , тоді
, тоді ![]()
![]()
![]() ;
;
б) для другої області ![]() ,
, ![]() , тоді
, тоді ![]() ;
; ![]() ;
; ![]() ;
;
в) для третьої області ![]() ,
, ![]() , тоді
, тоді ![]() ;
; ![]()
![]() ;
;
г) для четвертої області ![]() ,
, ![]() , тоді
, тоді ![]() ;
; ![]() ;
; ![]() .
.
Графіком нерівності є квадрат (рис. 20).
-
Побудувати графік нерівності
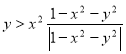 .
.
Розв’язання. Розглянемо два випадки:
а) ![]() , або
, або ![]() , тоді
, тоді ![]() ;
;
б) ![]() , або
, або ![]() , тоді
, тоді ![]() .
.
Графік нерівності зображено на рисунку 21. Бувають випадки, коли для розв’язування нерівностей з модулями не раціонально використовувати метод інтервалів.
-
Побудувати графік нерівності
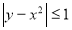 .
.
Розв’язання. Запишемо подвійну нерівність ![]() ;
; ![]() , звідки:
, звідки: 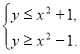 .
.
(рис. 22)
Розглянемо другий спосіб застосування методу інтервалів.
-
Побудувати графік нерівності
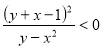 .
.
Розв’язання. Ліва частина нерівності є функція двох змінних: 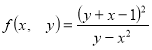 ;
; ![]() ,
, ![]() , якщо
, якщо ![]() .
.
Лінії ![]() і
і ![]() розбивають всю площину на дві області, у кожній з яких
розбивають всю площину на дві області, у кожній з яких ![]() зберігає знак. Щоб встановити цей знак, беремо контрольні точки (рис. 23).
зберігає знак. Щоб встановити цей знак, беремо контрольні точки (рис. 23).
-
Побудувати графік нерівності
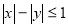 .
.
Розв’язання. Запишемо ![]() , тоді
, тоді ![]() . Функція
. Функція ![]() визначена для всіх
визначена для всіх ![]() і
і ![]() і дорівнює нулю, коли
і дорівнює нулю, коли ![]() . Легко встановити що при переході
. Легко встановити що при переході ![]() частини графіка функції, які відповідають від’ємним значенням
частини графіка функції, які відповідають від’ємним значенням ![]() , відкликаються, а ті, що лишилися , відображаються симетрично відносно осі
, відкликаються, а ті, що лишилися , відображаються симетрично відносно осі ![]() (чому?). Будуємо графік рівності
(чому?). Будуємо графік рівності ![]() . Записуємо ланцюжок: а)
. Записуємо ланцюжок: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() (рис. 24).
(рис. 24).
Розглянемо обернену задачу.
За виглядом графіків, зображених на рисунках 25, 26, 27, записати нерівності .
- За рисунком 25 записати нерівність.
Розв’язання. Аналізуючи рисунок 25, бачимо, що заштрихована частина площини обмежена графіком функції ![]() . Множину точок що розміщені над графіком функції
. Множину точок що розміщені над графіком функції ![]() , і точок, які належать цьому графіку, можна записати у вигляді нерівності
, і точок, які належать цьому графіку, можна записати у вигляді нерівності ![]() .
.
- За рисунком 26 записати нерівність.
Розв’язання. Спостерігаючи положення прямих, які обмежують заштрихований квадрат, записуємо їх рівняння: ![]() ;
; ![]() ;
; ![]() ;
; ![]() . У кожному координатному куті матимемо відповідну нерівність:
. У кожному координатному куті матимемо відповідну нерівність:
якщо ![]() і
і ![]() , то
, то ![]() , або
, або ![]() ,
,
якщо ![]() і
і ![]() , то
, то ![]() , або
, або ![]() ,
,
якщо ![]() і
і ![]() , то
, то ![]() , або
, або ![]() ,
,
якщо ![]() і
і ![]() , то
, то ![]() , або
, або ![]() .
.
Робимо висновок. Квадрат, обмежений прямими: ![]() ,
, ![]() ,
, ![]() ,
, ![]() є графіком нерівності
є графіком нерівності ![]() .
.
11. За рисунком 27 записати нерівність.
Розв’язання. Гіпербола, зображена на рисунку 27, записується рівнянням ![]() . Якщо
. Якщо ![]() , то
, то ![]() , що рівносильно нерівності
, що рівносильно нерівності ![]() . Крім того, нерівності
. Крім того, нерівності ![]() задовольняють також координати точок осі
задовольняють також координати точок осі ![]() . Отже, графік ,зображений на рисунку 27, записується нерівністю
. Отже, графік ,зображений на рисунку 27, записується нерівністю ![]() .
.
- Взаємозв’язок теорії з практикою в процесі
вивчення математики
Задача. Якою може бути власна швидкість моторного човна і швидкість течії річки, щоб 1,2км за течією човен проходив за час, не менший 1хв 48сек, а цю ж відстань проти течії – за час, не більший 2хв 24сек?
Розв’язання. Нехай власна швидкість човна і швидкість течії відповідно будуть: ![]() та
та ![]() (мал. 14).
(мал. 14).
Тоді ![]() і
і ![]() будуть швидкості, а
будуть швидкості, а ![]() і
і ![]() - час руху човна відповідно за течією та проти течії.
- час руху човна відповідно за течією та проти течії.
За умовою задачі маємо: 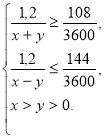
Після спрощення: 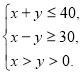
Далі: 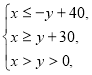 звідки
звідки ![]()
Із подвійної нерівності випливає: ![]() ,
, ![]() .
.
Беручи до уваги, що ![]() , матимемо:
, матимемо: ![]() .
.
Відповідь: ![]()
Наприклад, нехай швидкість течії буде 4км/год. Тоді ![]() , тобто швидкість човна може бути від 34км/год до 36км/год включно, і при цьому виконуються умови задачі, що видно із таких міркувань. Коли х= 35км/год, то швидкість човна за течією 39км/год, а проти – 31км/год і час його руху за течією
, тобто швидкість човна може бути від 34км/год до 36км/год включно, і при цьому виконуються умови задачі, що видно із таких міркувань. Коли х= 35км/год, то швидкість човна за течією 39км/год, а проти – 31км/год і час його руху за течією ![]() , що не менше 1хв 48сек, а проти течії
, що не менше 1хв 48сек, а проти течії ![]() , що не перебільшує 2хв 24сек.
, що не перебільшує 2хв 24сек.
Графічно цей розв’язок виражається множиною точок ![]() (мал. 28):
(мал. 28): 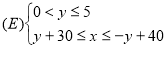
Якщо взяти будь-яку точку ![]() , включаючи точки бічних сторін, то її координати, відповідно взяті за власну швидкість човна й швидкість течії, задовольняють умову даної задачі.
, включаючи точки бічних сторін, то її координати, відповідно взяті за власну швидкість човна й швидкість течії, задовольняють умову даної задачі.
Вправи. 1. Зобразити геометрично та записати за допомогою явних нерівностей множину Е розв’язків систем:
а)![]() б)
б)![]() в)
в)![]()
2. Чи належать точки ![]() ,
, ![]() множинам розв’язків систем:
множинам розв’язків систем:
а) ![]() б)
б) ![]()
в) 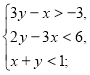 г)
г) 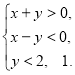
3. Задачі.
а) При проектуванні танкера береться до уваги, що його підіймальна сила повинна бути не меншою 11000![]() при питомій вазі води, що дорівнює 1,1
при питомій вазі води, що дорівнює 1,1![]() , і не меншою 9000
, і не меншою 9000![]() при питомій вазі води 0,96
при питомій вазі води 0,96![]() .
.
Визначити множину доступних значень ваги цього танкера та об’єму його підводної частини.
б) Маємо металевий брухт двох сортів: з 30 – процентним і 45 – процентним складом міді. Яку кількість брухту кожного сорту можна брати, щоб при змішуванні одержати сплав, який мав би в своєму складі не менше 35%, але не більше 40% міді?
в)Куплено двох сортів сукна по 8грн. та по 5грн, за 1м. Скільки сукна можна купити першого і другого сорту, щоб уся покупка коштувала не менше 50грн. і не більше 65грн.?
г) Куплено двох сортів сукна по 8грн. та по 5грн, за 1м. Скільки сукна другого сорту можна купити при умові, що першого сорту потрібно купити не менше 2м ы не більше 5м.?
4. Подано геометрично зображені деякі множини (на малюнках вони заштриховані). Записати їх за допомогою явних нерівностей, зваживши на те, що границі множин включаються до них (мал. 29, 30, 31, 32).
7. Графічні методи розв’язування рівнянь та нерівностей з параметрами
1.1 При яких ![]() система нерівностей
система нерівностей ![]() має розв’язок?
має розв’язок?
Розв’язання. Якщо межі півплощин, які задають нерівності системи, перетинаються, то дана система має розвֹязки.
Очевидно, що ![]() не підходить. Якщо
не підходить. Якщо ![]() , то рівняння меж півплощин перепишемо в такому вигляді:
, то рівняння меж півплощин перепишемо в такому вигляді: ![]() і
і ![]() . Ці прямі перетинаються, якщо
. Ці прямі перетинаються, якщо ![]() , тобто
, тобто ![]() і
і ![]() .
.
Зрозуміло, що розв’язуваня не завершене, адже паралельність меж ще не озхначає, що вихідна система не має розв’язків. Тому необхідно розглянути випадки ![]() і
і ![]() . Якщо
. Якщо ![]() , то межі збігаються, і, очевидно, що система розв’язків не має (нерівності системі задають різні півплощини).
, то межі збігаються, і, очевидно, що система розв’язків не має (нерівності системі задають різні півплощини).
Якщо ![]() , то маємо:
, то маємо: ![]() Ця система також розв’язків не має.
Ця система також розв’язків не має.
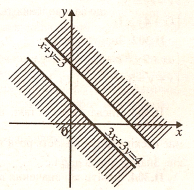 Отже,
Отже, ![]() не підходить.
не підходить.
Відповідь. ![]() і
і ![]() .
.
рис. 1.1
2.1
Знайти всі значення ![]() , при яких будь-який розв’язок нерівності
, при яких будь-який розв’язок нерівності ![]() за модулем не більший від 2.
за модулем не більший від 2.
Розв’язання. Перепишемо дану нерівність у такому вигляді: ![]() .
.
Графіки рівнянь ![]() й
й ![]() розбивають координатну площину
розбивають координатну площину ![]() на чотири області.(рис. 2.1).
на чотири області.(рис. 2.1).
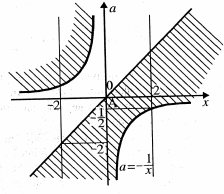 Тепер, якщо при деякому фіксованому значенні
Тепер, якщо при деякому фіксованому значенні ![]()
пряма ![]() в перетині з отриманою областю дає лише точки, абсциси яких задовольняють умову
в перетині з отриманою областю дає лише точки, абсциси яких задовольняють умову
рис 2.1
![]() , то
, то ![]() - одне із шуканих значень параметра. Тоді очевидно що всі
- одне із шуканих значень параметра. Тоді очевидно що всі ![]() з відрізка АВ складають
з відрізка АВ складають
Відповідь: ![]() .
.
3.1
Розв’язати нерівність ![]() .
.
Розв’язання. Наступна сукупність двох систем рівносильна заданій нерівності: ![]() або
або 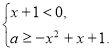
При об’єднанні графічних образів кожної із цих систем слід врахувати, що пряма ![]() дотика ється до параболи
дотика ється до параболи ![]() у точці (-1: 1).
у точці (-1: 1).
Отже на рис. 3.1 зображено всі розв’язки вихідної нерівності. Горизонтальні прямі, що перетинають цю множину, перетинають її по відрізку ( за винятком однієї прямої ![]() ).
).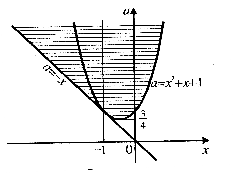 Очевидно, що абсциси всіх точок цього Рис 3.1 відрізка і будуть розв’язками даної нерівності. Для отримання відповіді залишилося виразити
Очевидно, що абсциси всіх точок цього Рис 3.1 відрізка і будуть розв’язками даної нерівності. Для отримання відповіді залишилося виразити ![]() через
через ![]() у рівнянні
у рівнянні ![]() . Якщо
. Якщо ![]() , то маємо
, то маємо ![]() .
.
4.1
Розв’язком нерівності з двома зміними ![]() та
та ![]() називають впорядковану пару змінних (
називають впорядковану пару змінних (![]() ;
; ![]() ), яка перетворює нерівність у правильну числову.
), яка перетворює нерівність у правильну числову.
Графіком нерівності з двома змінними називають множину точок координатної площини, координати яких є розв’язком нерівності.
Приклад: побудувати графік нерівності ![]() .
.
-
область визначення виразу
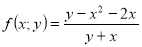
![]() .
.
-
нулі виразу
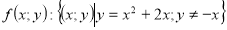 .
.
3)Зобразимо область визначення і нулі виразу ![]() на координатній площині. Визначимо знак виразу на кожній з отриманих областей.
на координатній площині. Визначимо знак виразу на кожній з отриманих областей.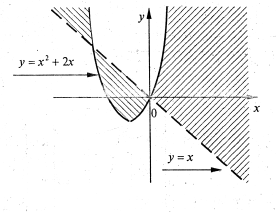 Виділимо штриховою лінією ті області, координати точок яких задовольняють дану нерівність
Виділимо штриховою лінією ті області, координати точок яких задовольняють дану нерівність
рис 4.1
5.1При яких значеннях параметра ![]() нерівність
нерівність ![]() виконується при всіх
виконується при всіх ![]() ?
?
Побудуємо графік нерівності в системі координат ![]()
![]() . Для цього визначимо:
. Для цього визначимо:
-
ОДЗ:
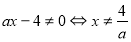 ;
;
-
нулі виразу
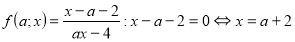 .
.
Таким чином , дістаємо графік:
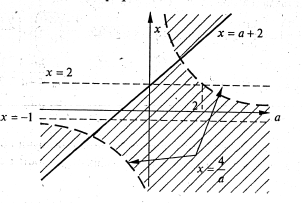
рис 5.1
З графіка нерівності знаходимо відповідь : ![]() .
.
6.1
При всіх значеннях пареметра ![]() розв’язати нерівність
розв’язати нерівність ![]() .
.
-
ОДЗ
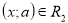 ;
;
-
Прямі
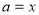 і
і 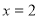 розбивають координатну площину
розбивають координатну площину  на 4 області. На кожній з них спростимо дану нерівність і побудуємо її графік.
на 4 області. На кожній з них спростимо дану нерівність і побудуємо її графік.
|
Область |
1 |
2 |
3 |
4 |
|
Нерівність |
|
|
|
|
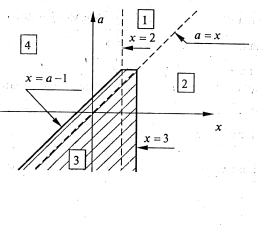
рис. 6.1
Відповідь. При ![]() ; при
; при ![]() .
.
7.1
На координатній площині зобразити множину пар ![]() , для кожної з яких рівняння
, для кожної з яких рівняння ![]() має чотири різних дійсних корені.
має чотири різних дійсних корені.
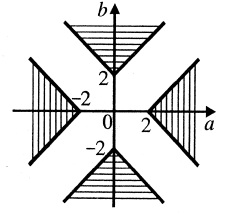 Розв’язання.
Розв’язання. ![]() і
і ![]() - дискримінанти квадратних тричленів, що розміщені відповідно в першій і другій дужках. Для виконання умови задачі необхідно
- дискримінанти квадратних тричленів, що розміщені відповідно в першій і другій дужках. Для виконання умови задачі необхідно 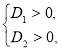 тобто
тобто 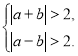
На координатній площині ![]() неважко зобразити розв’язок останьої системи (рис 7.1). рис. 7.1 Але помилково вважати отриману множину точок шуканою відповіддю. Ми не вказуватимемо відразу на помилку, хоча, ймовірно, читач сам може це зробити.
неважко зобразити розв’язок останьої системи (рис 7.1). рис. 7.1 Але помилково вважати отриману множину точок шуканою відповіддю. Ми не вказуватимемо відразу на помилку, хоча, ймовірно, читач сам може це зробити.
Розв’язування цьго прикладу проходить за такою схемою. Визначаємо сукупність рівносильну даному рівнянню (системі). Потім окремо знаходимо кількість розв’язків кожного рівняння (системи) сукупності. Імовірність появи помилки зростає на останьому етапі, коли визначається загальна кількість розв’язків вихідного рівняння (системи). Причина – «механічне» об’єднання раніше отриманих розв’язків. Так немає жодних гарантій, що при певних значеннях параметрів розв’язки не збігаються.
Оскільки добуток коренів квадратних тричленів дорівнює 1 (нагадаємо, що існування таких коренів визначено умовами ![]() і
і ![]() ), то якщо один із коренів першого тричлена збігається з яким-небуть коренем другого, тоді обов’язково збігатимуться й інші корені. Таким чином, збіг яких-небудь коренів призводить до необхідності виконання рівності
), то якщо один із коренів першого тричлена збігається з яким-небуть коренем другого, тоді обов’язково збігатимуться й інші корені. Таким чином, збіг яких-небудь коренів призводить до необхідності виконання рівності ![]() , тобто
, тобто ![]() . Отже, з отриманої множини точок (рис. 7.1) потрібно виключити промені
. Отже, з отриманої множини точок (рис. 7.1) потрібно виключити промені ![]() і
і ![]() осі абсцис.
осі абсцис.
8.1
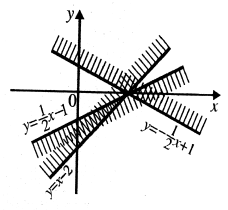
При яких ![]() система нерівностей
система нерівностей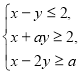 має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання. Кожна з нерівностей системи задає півплощину разом з границею на координатній площині ![]() . Якщо які-небуть дві із границь паралельні або збігаються, то очевидно, що система не може мати єдиного розв’язку. Тоді перетин розв’язків будь-яких двох нерівностей повинен задавати область, обмежену кутом (включати границю).Отже, якщо границя третьої півплощини не пройде через точку перетину двох інших границь, то система також не може мати єдиного розв’язку (розв’язків буде нескінченна кількість або жодного). Тоді всі три границі повинні проходити через одну точку. Щоправда, ця умова ще не гарантує єдиності розв’язку, а, отже, вона є необхідною.
. Якщо які-небуть дві із границь паралельні або збігаються, то очевидно, що система не може мати єдиного розв’язку. Тоді перетин розв’язків будь-яких двох нерівностей повинен задавати область, обмежену кутом (включати границю).Отже, якщо границя третьої півплощини не пройде через точку перетину двох інших границь, то система також не може мати єдиного розв’язку (розв’язків буде нескінченна кількість або жодного). Тоді всі три границі повинні проходити через одну точку. Щоправда, ця умова ще не гарантує єдиності розв’язку, а, отже, вона є необхідною.
Таким чином, система 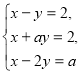 повинна мати розв’язки.
повинна мати розв’язки.
Із першого і третього рівнянь системи встановлюємо, що ![]() ,
, ![]() . Підставивши ці значення у друге рівняння, знайдемо умови, за яких система рівнянь має розв’язки. Отримуємо
. Підставивши ці значення у друге рівняння, знайдемо умови, за яких система рівнянь має розв’язки. Отримуємо ![]() . Звідси
. Звідси ![]() або
або ![]() . Серед цих значень і міститься відповідь.
. Серед цих значень і міститься відповідь.
Якщо ![]() , то
, то 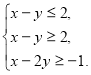
 Оскільки границі півплощин, які задають перші дві нерівності цієї системи, збігаються, то, як зазначалося вище, ця система не може мати єдиного розв’язку.
Оскільки границі півплощин, які задають перші дві нерівності цієї системи, збігаються, то, як зазначалося вище, ця система не може мати єдиного розв’язку.
Якщо ![]() , то запишемо
, то запишемо 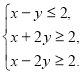
Зобразивши розв’язки кожної нерівності системи (рис. 8.1), встановлюємо, що вони мають тільки одну спільну точку.
рис. 8.1 Відповідь. ![]()
8. Математичне мистецтво Моріца Ешера
Серед сучасних художників в жанрі «математичного мистецтва» найбільш успішно виступає голандський художник Моріц Ешер.
«Я часто відчуваю більшу близькість до математики, ніж до колег – художників», - писав сам Ешер. Його літографіїї, гравюри на дереві можна побачити в кабінетах математиків та інших учених в різних куточках світу. Його роботи містять глибокі філосовські задуми та математичні спостереження.
Серед його творів найбільшою популярністю користуються орнаменти, які заповнюючи площину і переходячи в простір, оживають. Орнаменти складаються із періодичних повторень конгруентних фігур. Розбиваючи площину на хитроумні комбінаціїї контурів пахів, риб, людських фігур, Ешер вміло компонує із даних фігур незвичайні, наповнені певним змістом комбінації.
На літографії «Рептиліїї» маленькі чудовиська виповзають із шестикутної мозаїки, щоб почати короткий цикл трьохмірного буття. Досягаючи вищої точки, виповзаючи на додекаедр, рептилії знову повертаються в площину.
На гравюрі «День і ніч» права і ліва частина композиції не тільки дзеркально симетричні, а й служать своєрідними «негативами» одна одній. Квадрати полів перетворюються в білих птахів, які летять в ночі, і в чорних птахів, які летять на фоні світлого денного неба.
На круглій гравюрі «Рай і пекло» фігури ангелі і кажанів заповнюють всю площину.
«Коли я малюю, я перебуваю під владою істот, породжених моєю уявою. Вони ніби самі вибирають, в якому вигляді їм появитися... Лінія, яка розділяє дві суміжні фігури, виконує подвійну функцію: побудувати фігуру і передати зміст даної картини. Провести таку лінію дуже складно. По дві сторони від неї набуває видиму форму те, що раніше існувало тільки в уяві. Але ні людський зір, ні людський розум не можуть одночасно бачити і усвідомлювати дві речі, тому весь час відбувається швидке і неперервне переключення уваги з однієї сторони лінії на іншу. В цьому суть трудності, яка захована в моїх картинах»,- писав Ешер.
Якщо вам покажеться, що створення таких орнаментів- справа легка, ми рекомендуємо випробувати свої сили і придумати хоч би одну композицію!
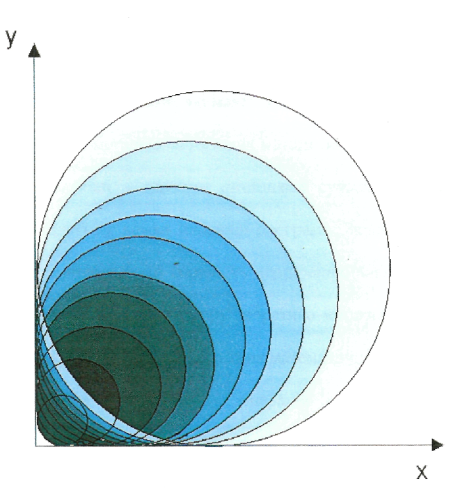
Наприклад: елемент побудови композиції задається формулою ![]() ,
,
![]()
![]()
9.Висновки
«Математичні відомості можуть застосовуватися вміло і корисно тільки в тому разі, якщо вони засвоєні творчо, так, що учень бачить сам, як можна було б прийти до них самостійно»
О.М.Колмогоров
Проведене нами дослідження дозволяє зробити такі висновки: специфіка нестандартних методів розв'язування рівнянь та нерівностей сприяють розвитку самостійного математичного мислення.Матеріал посібника корисний для учнів, які мають намір вивчати математику в майбутньому.
Основна мета навчання юних математиків - ознайомлення на доступному для учнів рівні з деякими питаннями сучасної математики та задачами, які виходять за рамки шкільної програми. Залишаючись в межах елементарної математики, вони сприяють поширенню знань по розв'язуванню рівнянь та нерівностей з точки зору теоретико-множинної інтерпретації, допомагають орієнтуватися в нестандартних математичних ситуаціях.
Поняттю про множину, операцій над множинами в шкільному курсі приділяється дуже мало уваги, хоч це має велике освітнє та пізнавальне значення.
Ознайомлення з даним матеріалом поглиблює і розширює фактичні знання учнів, сприяє підвищенню наукового рівня знань, умінь і навичок. В сучасний період теорія множин є базою наукового розвитку математики, фізики, біології, логіки і тд.
10.Список використаної літератури
-
Колесник Б.М.Алгебраїчні задачі на дослідження. Київ,
«Радянська школа», 1971. -
Лобанова Л.В., Фінкельштейн Л.П. Вибрані задачі елементарної
математики. Київ, «Вища школа», 1989. -
Конфорович А.Г. Колумби математики. Київ, «Радянська школа».
1982. -
Зоря А.С., Кіро С.М. Про математику І математиків. Київ,
«Радянська школа», 1981. -
Шунда Н.М. Функції та їх графіки. Київ, «Радянська школа»,
1976. - Бевз Г.П. Довідник з математики. Київ, «Радянська школа», 1981.
-
Віленкін Н.Я. Функції в природі і техніці. Москва, «Освіта»,
1978. -
Коваленко В.Г., Кривошеєв В.Я., Старосєльцева О.В, Алгебра, 9.
Експериментальний навчальний посібник для 9 класу шкіл з
поглибленим вивченням математики і спеціалізованих шкіл
фізико-математичного профілю. Допущено міністерством освіти
України. 2-ге видання. Київ, «Освіта», 1996. -
Бевз Г.П. Методика розв'язування алгебраїчних задач. Київ,
«Радянська школа», 1975.
Ю.Возняк Г.М., Маланюк М.П. Взаємоз'язок теорії з практикою в процесі вивчення математики. Київ, «Радянська школа», 1989.
И.Гайштут О.П., Литвиненко Г.М. Розв'язування алгебраїчних задач. Київ, «Радянська школа», 1999.
 Додатки
Додатки
М. Ешер
«Є буття: та іменем яким його назвати?
Не сон воно і не переконання;
Між них воно, в людині з ним із пізнанням межує розуміння.»



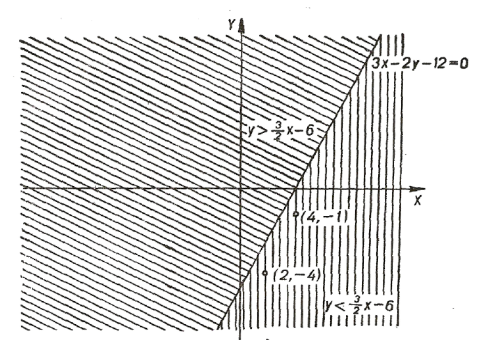 рис.1
рис.1
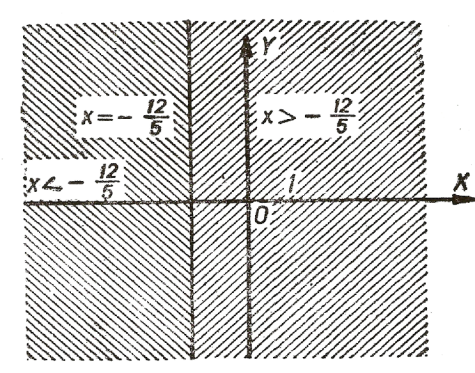
рис.2
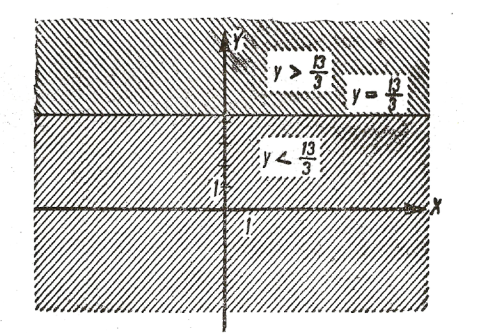 рис.3
рис.3
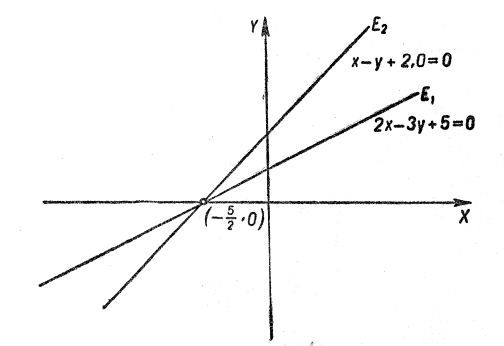
Рис.4
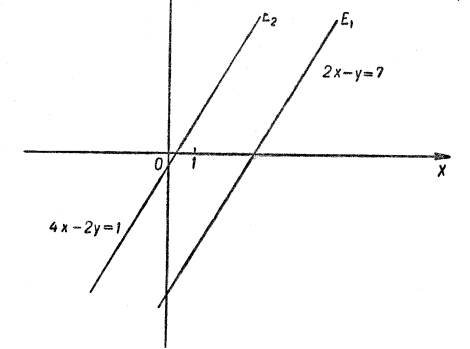
Рис.5
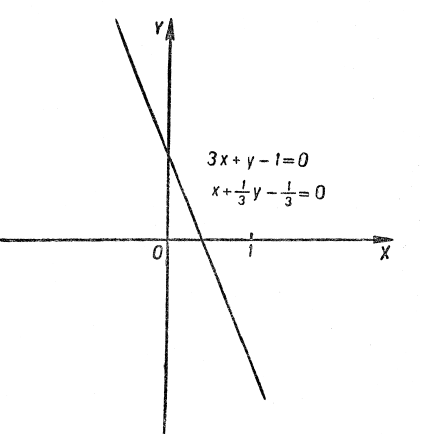
Рис.6
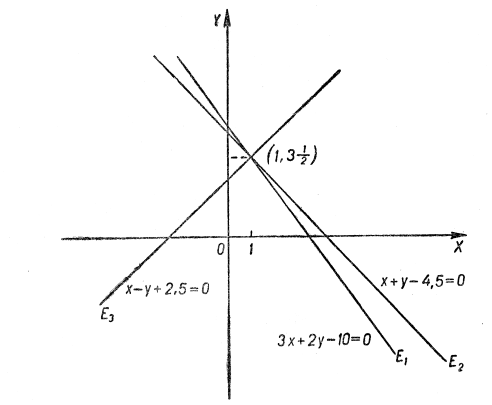
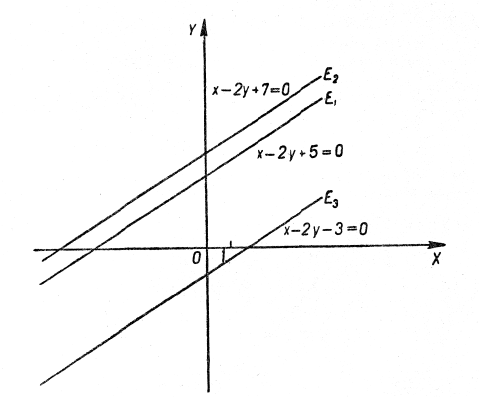 Рис.7
Рис.7
Рис.8
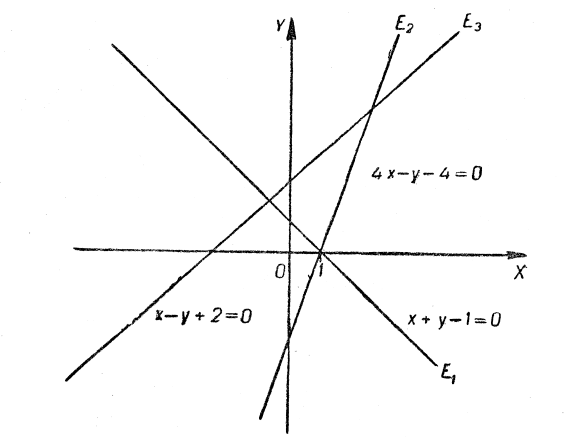
Рис.9
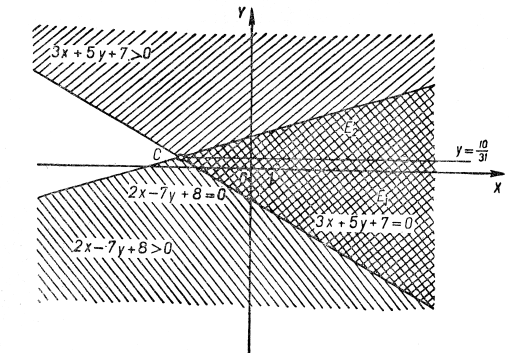
Рис.10
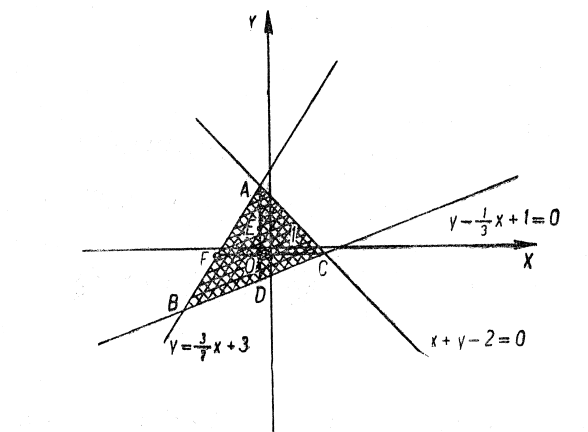
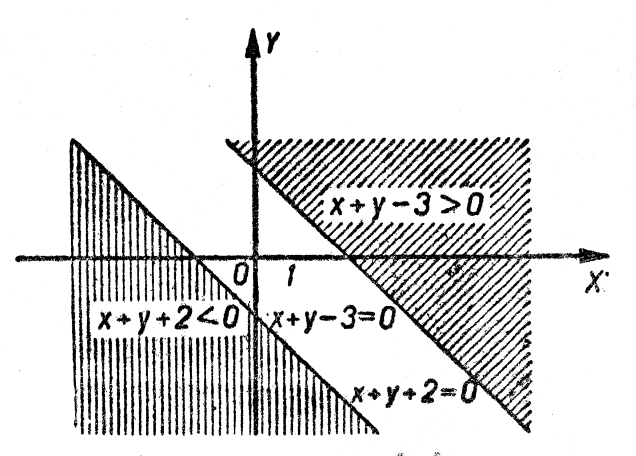 рис.11
рис.11
рис.12
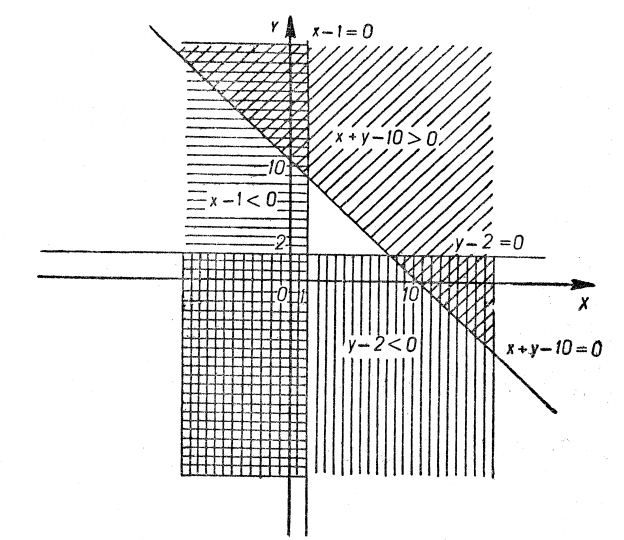 рис.13
рис.13
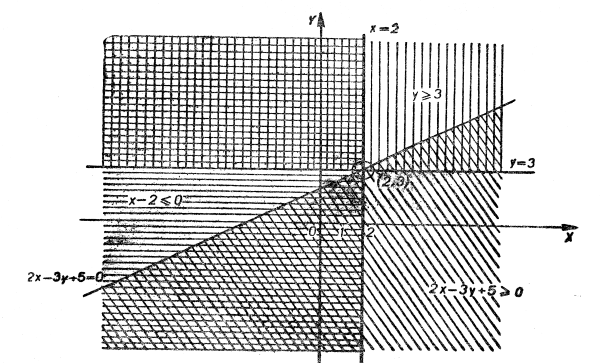 рис.14
рис.14
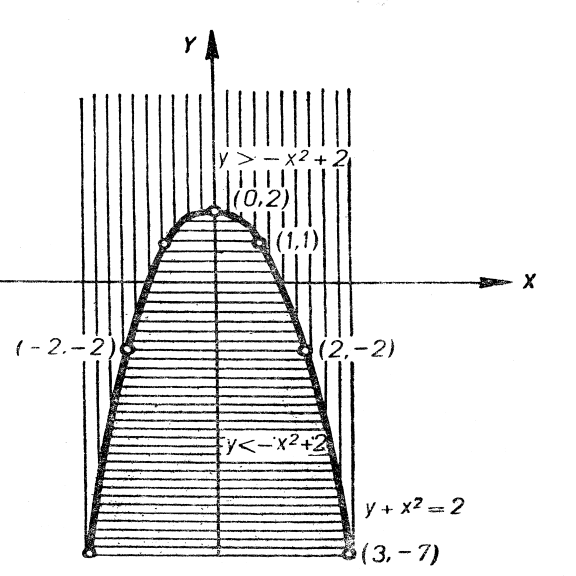 рис.15
рис.15
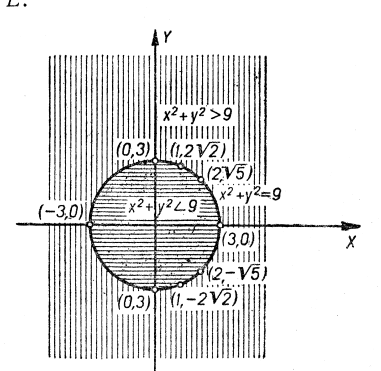
Рис.16
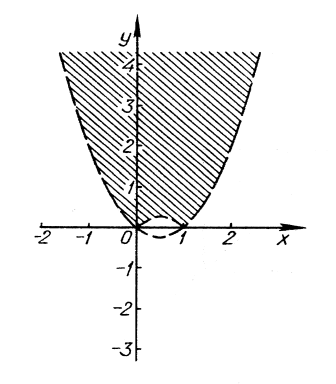
Рис.17
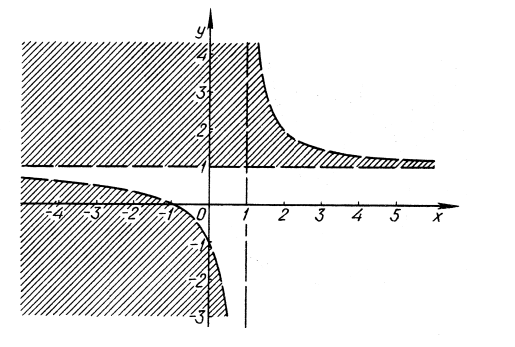 рис.18
рис.18
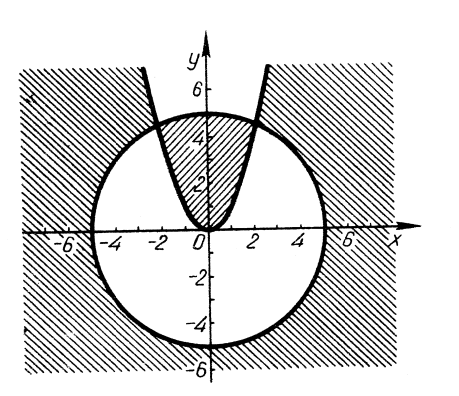
Рис.19
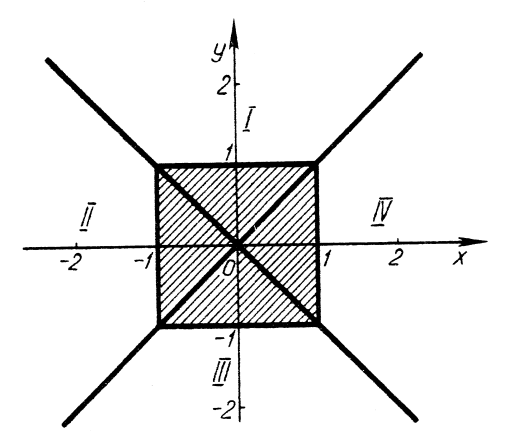 рис.20
рис.20
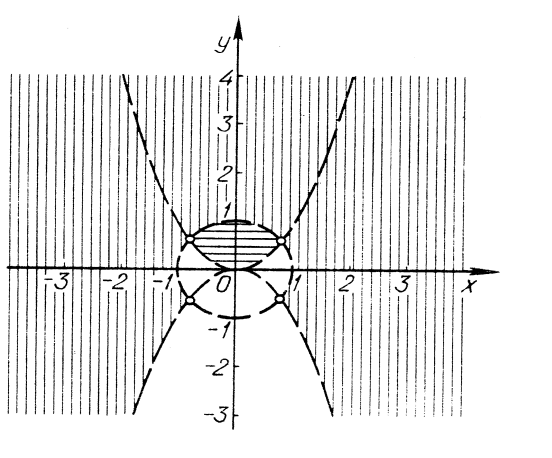 рис.21
рис.21
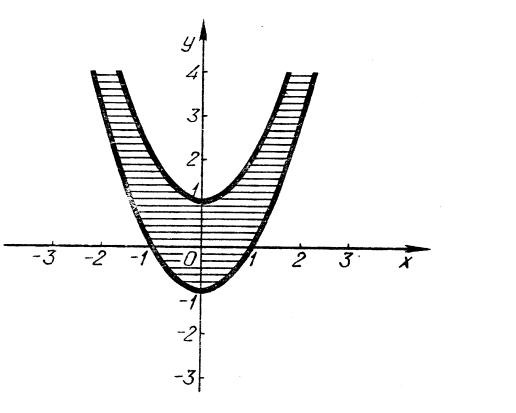 рис.22
рис.22
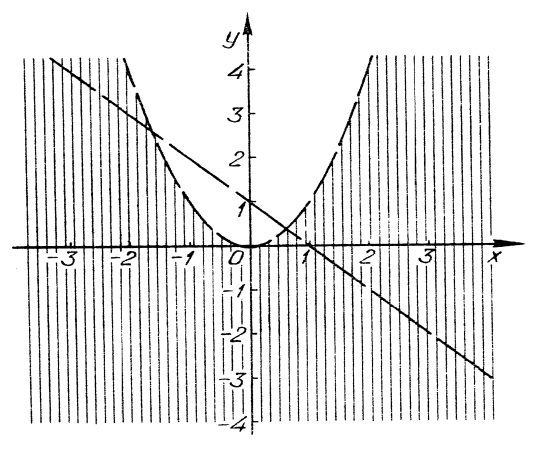 рис.23
рис.23
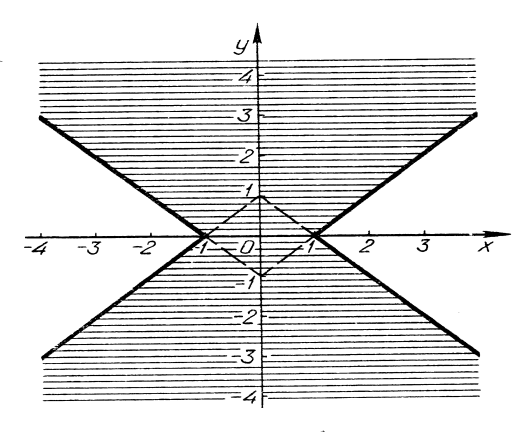 рис.24
рис.24
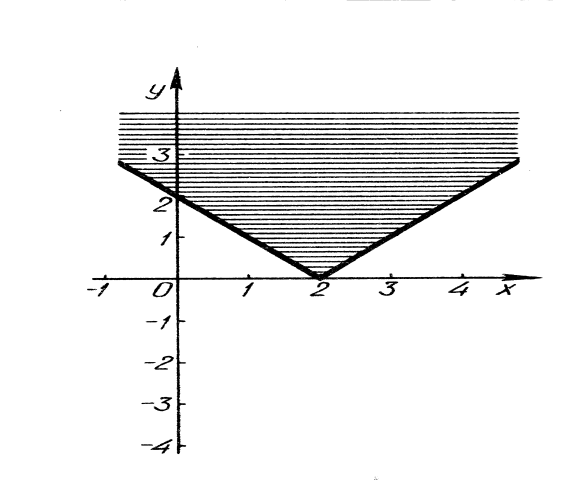 рис.25
рис.25
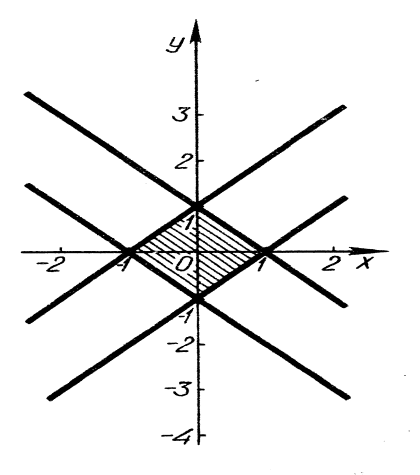 рис.26
рис.26
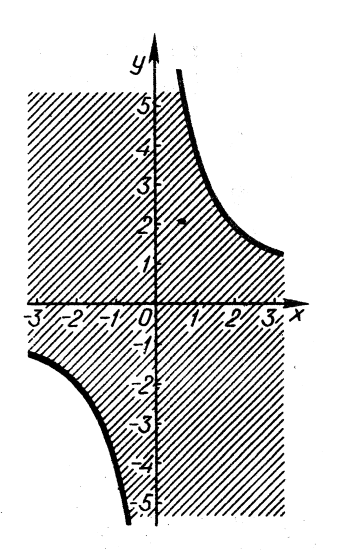 рис.27
рис.27
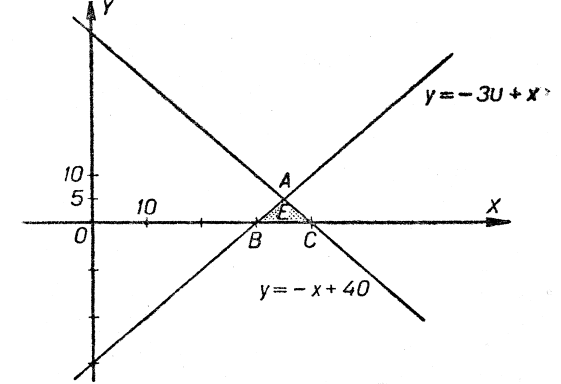
Рис.28
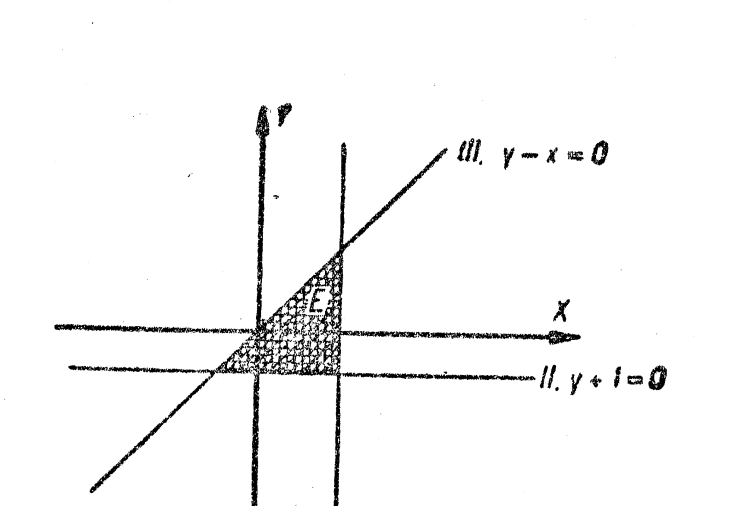 рис.29
рис.29
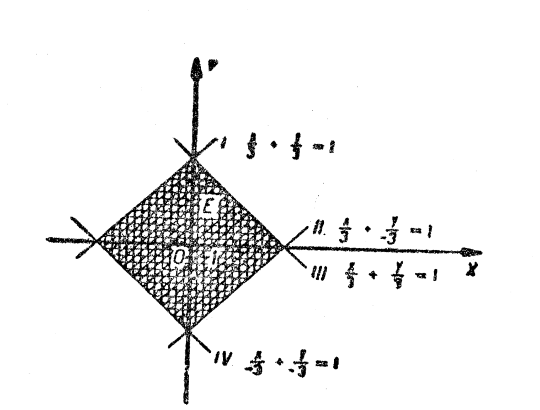 рис.30
рис.30

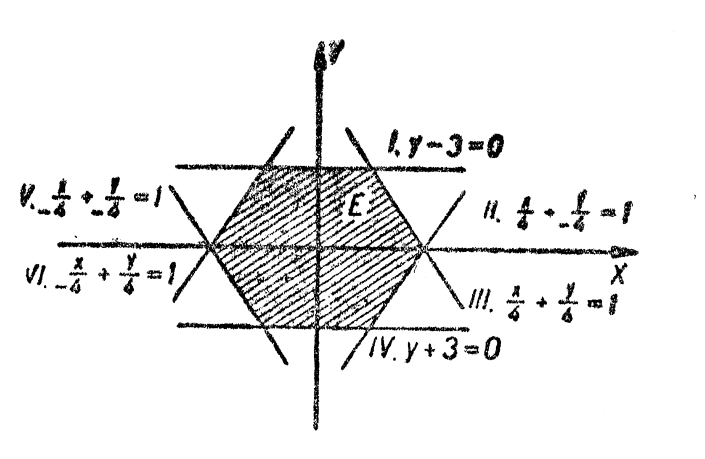 рис.31
рис.31
рис.32
1

про публікацію авторської розробки
Додати розробку