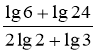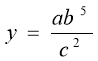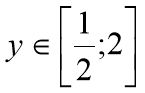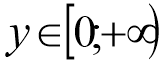Практичне заняття "Властивості логарифмів"
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ЛЬВІВСЬКИЙ ТЕХНІКО-ЕКОНОМІЧНИЙ КОЛЕДЖ
НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ «ЛЬВІВСЬКА ПОЛІТЕХНІКА»
Сценарій проведення заняття
з елементами гри “Математичне лото”
на тему:
“Застосування властивостей логарифмів”
ЛЬВІВ
Тема: Показникова функція. Властивості логарифмів.
Навчальна мета: Повторити основні поняття та властивості функцій, зокрема показникової; властивості логарифмів; формування вмінь та навичок у використанні основної логарифмічної тотожності, логарифмування та потенціювання виразів.
Виховна мета. Формувати наполегливість, увагу та зосередженість студентів.
Напис на дошці: Математика цікава тоді, коли
дає поживу нашій винахідливості
й здатності до міркувань.
Д.Пойа.
Обладнання: кодоскоп.
Організація групи до заняття: Повторити весь теоретичний матеріал та переглянути практичні завдання в конспектах, які вони виконували на попередньому занятті та вдома.
Організація гри:
Для кожної команди необхідно заздалегідь підготувати по два цупкі листи паперу, щоб на одному з них (з одного боку) був кольоровий малюнок. Ці листи потрібно розділити на 25 рівних частин. На одному листі (основа) кожна частинка нумерується, і у ній записуються завдання, а на другому листі (з малюнком) на чистій стороні – відповідно відповіді до завдань. Другий лист розрізається на прямокутники, фрагменти малюнка змішуються, формується п’ять пакетів по п’ять карток у кожному.
Крім цього, для кожної команди слід приготувати третій цупкий лист паперу, про роль якого буде сказано пізніше.
Важливо, щоб кожний пакет і картки у ньому мали свій порядковий номер.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
6 |
11 |
16 |
21 |
|
2 |
7 |
12 |
17 |
22 |
|
3 |
8 |
13 |
18 |
23 |
|
4 |
9 |
14 |
19 |
24 |
|
5 |
10 |
15 |
20 |
25 |
Це основа, у клітинках якої Це лист з малюнком, на чистій
записані завдання. стороні якого у клітинках вписані
відповіді до відповідних завдань.
Правила гри. Гра відбувається у два тури.
Перший тур – теоретичний (відбірковий).
У ньому беруть участь усі студенти групи. Викладач зачитує запитання. Студент, який першим відповідає на нього, стає учасником другого туру. Таким чином набираються 4 команди по 5 осіб у кожній. Решта студентів стають помічниками викладача, з них обирають 4 спостерігачів та 4 експертів по одному на кожну команду, а також двох ведучих гри. (Кількість учасників гри можна корегувати в залежності від загальної кількості осіб у групі.)
Другий тур – практичний (сама гра).
Ведучий читає одне з 25-ти завдань другого туру. Якщо є необхідність, тоді другий ведучий проектує це завдання на екран за допомогою кодоскопа (кодопозитиви підготовлені викладачем заздалегідь). Студенти – члени команд уважно слухають завдання, при потребі розв’язують його письмово в зошиті. Відповідь міститься на картці в одного з членів кожної команди. Тоді цю картку слід покласти на відповідну клітинку листа основи малюнком до нього, а відповіддю догори.
Якщо одночасно у декількох членів однієї команди знайшлася картка з правильною відповіддю (що є неможливо!), тоді вони мають право на обговорення. Коли один з учасників обговорення впевнений у своїй правоті, тоді він кладе свою картку на потрібну клітинку таблиці, а решта учасників відмічають свої “засвічені” картки у експертів.
Якщо ж під час обговорення студенти не прийшли до спільної думки, тоді вони усі за це отримують по одному штрафному балу.
Так ведучі зачитують усі 25 завдань, а таблиці кожної команди поступово покриваються картками з відповідями.
Тоді експерт кожної команди накриває таблицю третім листом і обережно перевертає все це на другий бік. Коли знімається верхня основа, тоді усі бачать чотири чудові кольорові картини (при умові, що всі учасники команд правильно розв’язали всі завдання).
Умови оцінювання. Експерти та спостерігачі разом оцінюють результати гри. Якщо картина вийшла правильною, тоді команда виграє, і усі її члени отримують оцінку “10”. Якщо ж є помилки, тоді це також виявиться по картині. Та картка, що псує зображення, вилучається. Картка пронумерована, а отже відомий учасник гри, який припустився помилки. За це його оцінка знижується на два бали, а його команда уже не може претендувати на перемогу у грі. Кожний учасник команди, яка програла, втрачає по одному балу за кожну допущену в команді помилку, а винуватець помилки – по два штрафних бали. Найбільш активні студенти у відбірковому турі додатково отримують один бал.
Хід заняття: Повідомляється тема і мета заняття, форма його проведення, а також правила гри та умови оцінювання.
Актуалізація опорних знань (І тур).
- Сформулювати означення функції. Що називають областю визначення функції? Що називають областю значень функції?
- Яка функція називається показниковою? Якою є область визначення та область значень показникової функції?
- У якому випадку область значень показникової функції буде лише від’ємною?
- Сформулювати означення функції, яка зростає на проміжку. Яка умова зростання показникової функції?
- Сформулювати означення функції, яка спадає на проміжку. Яка умова спадання показникової функції?
- Чи симетричний графік показникової функції відносно осі ОУ? Як називається властивість функції, що визначає таку симетрію графіка?
- Чи може графік показникової функції бути симетричним відносно осі ОУ? Відповідь пояснити.
- Чому основа показникової функції не може дорівнювати 1?
- Що є спільного для графіків усіх показникових функцій незалежно від основи а?
-
Які з вказаних функцій є показниковими: у=х2, у=(-3)х, у=
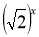 , у=(х-2)3, у=πх , у=5-х?
, у=(х-2)3, у=πх , у=5-х?
- Які з вказаних функцій є зростаючими і які спадними:
а)у=5х; б)у=(0,5)х; в)у=![]() ; г)у=πх; д) у=
; г)у=πх; д) у=![]() ; е)у=
; е)у=![]() ; є)у=(14cos
; є)у=(14cos![]() )-х?
)-х?
- Чи є серед значень функції у=3х найбільше та найменше значення?
- Що називається логарифмом числа за даною основою?
- За означенням логарифма вказати, яке з трьох вказаних тверджень є справедливим: а) логарифм – степінь; б) логарифм – показник степеня; в) логарифм – основа степеня?
- Дано рівність 27⅔=9. Що тут є логарифмом, якого числа і за якою основою?
-
Чи правильно, що
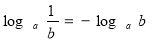 ?
?
-
Яку дію треба виконати, щоб з рівності lg x=
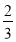 lg a отримати рівність
lg a отримати рівність 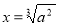 ?
?
- Назвіть дію, обернену до потенціювання.
- Довести, що loga2+loga0.5=0.
- Чи правильно, що logaab=1+logab?
Узагальнення та систематизація раніше здобутих знань (ІІ тур).
-
Знайти область визначення функції
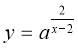 .
.
- Знайти область визначення функції y=atg x.
- Знайти область значень функції y=2cos x.
- Знайти область значень функції y=3 x.
- Знайти найбільше та найменше значення функції y=5sin x-1.
-
Знайти найбільше та найменше значення функції
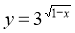 .
.
-
Знайти найбільше та найменше значення функції
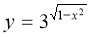 .
.
-
Знайти х, якщо
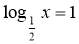 .
.
-
Знайти х, якщо
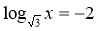 .
.
-
Знайти х, якщо
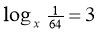 .
.
-
Знайти х, якщо
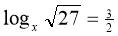 .
.
-
Знайти х, якщо
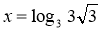 .
.
-
Знайти х, якщо
 .
.
-
Знайти х, якщо
 .
.
-
Обчислити:
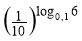 .
.
-
Обчислити:
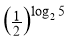 .
.
-
Обчислити:
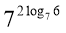 .
.
-
Обчислити:
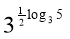 .
.
-
Обчислити:
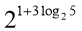 .
.
-
Обчислити:
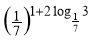 .
.
- Обчислити: log0,39-2∙log0,3100.
- Обчислити: 4∙log525-5∙log416.
-
Обчислити:
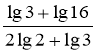 .
.
-
Прологарифмувати вираз за основою 10:
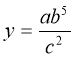 .
.
-
Прологарифмувати вираз за основою 10:
 .
.
Підсумок заняття: Як працювала група? Як працювали окремі студенти? Чи досягли мети заняття?
Оцінювання. Вивчаються вилучені картки, визначається команда – переможець; викладач виставляє оцінки відповідно до результатів кожного учасника гри.
Домашнє завдання:
- Порівняти з одиницею 2-5, (¾)-2, (π/3)√13.
- Знаючи, що lg 2=a, log27=b, знайдіть lg 56.
- Знаючи, що lg 3=a, lg 2=b, знайдіть log56.
- Виразити через а і b: а) log420, якщо lg 2=a;
б) log4932, якщо log214=a.
- Обчислити: log32log43log54log65log76log87.
-
Обчислити: а)
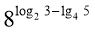 ; б)
; б) 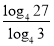 ; в)
; в) 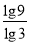 .
.
-
Обчислити без використання таблиць: а)
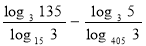 ;б)
;б)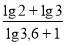 .
.
-
Прологарифмувати вирази: а)
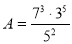 ; б)
; б) 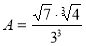 .
.
- Пропотенціювати вираз: lg x= lg2+lg a+3lg b-lg3-¼lg(b-a).
Відповіді:
- х(-;2)(2;+)
- х/2+k, k
-
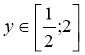
-
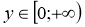
- ymax=1; ymin=1/25
- ymin=1
- ymax=3; ymin=1
- 1/2
- 1/3
- 1/4
- 3
- 3/2
- –3
- 7
- 6
- –5
- 36
- 5
- 250
- 9/7
- 2
- –2
- 4
- lg a+5lg b-2lg c
- lg a/5-lg b-2lg c
ДОДАТКИ:
|
1.
Знайти область визначення функції
|
6.
Знайти найбільше та найменше значення функції
|
11.
Знайти х, якщо
|
16.
Обчислити:
|
21. Обчислити: log0,381-2∙log0,3100.
|
|
2. Знайти область визначення функції y=atg x.
|
7.
Знайти найбільше та найменше значення функції
|
12.
Знайти х, якщо
|
17.
Обчислити:
|
22. Обчислити: 4∙log525-5∙log416.
|
|
3. Знайти область значень функції y=2cos x.
|
8.
Знайти х, якщо
|
13.
Знайти х, якщо
|
18.
Обчислити:
|
23.
Обчислити:
|
|
4. Знайти область значень функції y=3 x.
|
9.
Знайти х, якщо
|
14.
Знайти х, якщо
|
19.
Обчислити:
|
24.
Прологарифмувати вираз за основою 10:
|
|
5. Знайти найбільше та найменше значення функції y=5sin x-1.
|
10.
Знайти х, якщо
|
15.
Обчислити:
|
20.
Обчислити:
|
25.
Прологарифмувати вираз за основою 10:
|
|
х(-;2)(2;+) |
ymin=1 |
3 |
–5 |
4 |
|
х/2+k, k |
ymax=3; ymin=1 |
3/2 |
36 |
–2 |
|
|
1/2 |
–3 |
5 |
2 |
|
|
1/3 |
7 |
250 |
lg a+5lg b-2lg c |
|
ymax=1; ymin=1/25 |
1/4 |
6 |
9/7 |
lg a/5-lg b-2lg c |
1


про публікацію авторської розробки
Додати розробку