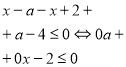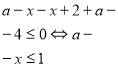Розв’язування нетрадиційних завдань з математики при підготовці учнів загальноосвітніх навчальних закладів до зовнішнього незалежного оцінювання
Зміст
|
Передмова……………………………………………………………………….. |
4 |
|
Розділ 1. Числа і вирази………………………………………………………... |
6 |
|
6 |
|
10 |
|
14 |
|
18 |
|
Розділ 2. Рівняння та системи рівняння……………………………………… |
22 |
|
2.1. Цілі та дробові раціональні рівняння……………………………… |
22 |
|
2.2. Ірраціональні та тригонометричні рівняння……………………… |
25 |
|
2.3. Показникові та логарифмічні рівняння……………………………. |
28 |
|
Розділ 3. Графічне розв’язування нерівностей та їх систем з двома невідомими …………………………………………………………………………………….. |
31 |
|
3.1. Системи лінійних нерівностей та рівнянь з двома невідомими……. |
31 |
|
3.2. Квадратні рівняння та нерівності з двома невідомими……………… |
36 |
|
3.3. Геометрична інтерпретація розв’язків нерівності з двома невідомими……………………………………………………………... |
38 |
|
3.4. Графічні методи розв’язування рівнянь та нерівностей з параметрами…………………………………………………………….. |
45 |
|
Використана та рекомендована література…………………………………… |
54 |
|
Додатки…………………………………………………………………………. |
56 |
Шановні читачі!
Посібник є збірником завдань, що охоплює такі теми шкільного курсу математики для 5 -11 класів: «Числа і вирази» , «Рівняння та системи рівнянь» «Графічне розв’язування нерівностей та їх систем з двома невідомими». До них належать, зокрема, завдання на достатність даних, завдання на встановлення відповідності між двома множинами об’єктів ( логічних пар), завдання на встановлення правильної послідовності дій та завдання на зображення у прямокутній системі координат множини розв’язків систем нерівностей з двома невідомими.
Зупинимося коротко на особливостях кожного з цих типів завдань.
Завдання на достатність даних. Особливістю цих завдань є те , що вони призначені для перевірки вміння проводити логічний аналіз задачі. Ці завдання найчастіше містять неповну початкову умову проблеми та її вимогу, а також додаткові дані (1) і додаткові дані (2). Учаснику тестування потрібно з’ясувати чи достатньо початкової умови разом із додатковими даними ( у різних поєднаннях) для розв’язання проблеми. Саму проблему при цьому розв’язувати не обов’язково.
Завдання на достатність даних можуть бути подані у вигляді завдань на порівняння значень двох величин (Х і У), які визначаються в умові. В цій ситуації знаходити значення самих величин не обов’язково. Потрібно з’ясувати, чи можна дати однозначну відповідь на поставлене запитання, виходячи з умови завдання.
У посібнику завдання на достатність даних та завдання на порівняння подані як завдання закритої форми з вибором однієї правильної відповіді.
Завдання на встановлення відповідності. Учаснику тестування пропонується встановити відповідність між двома множинами математичних об’єктів ( знайти логічні пари). Елементи першої множини позначаються цифрами, а елементи другої множини - літерами. У посібнику перша множина містить чотири елементи, занумеровані цифрами (1-4), а друга множина – п’ять елементів, позначених літерами (А-Д). Кожному елементу першої множини може відповідати тільки один елемент другої, а кожен елемент другої множини може відповідати не більше ніж одному елементу першої. Саме такий формат завдань для встановлення логічних пар використовується зараз в Україні під проведення ЗНО.
Завдання на встановлення послідовності. Учаснику тестування пропонується серед наведених логічних кроків, які позначено літерами, вибрати необхідні та скласти алгоритм розв’язування математичної задачі – відтворити правильну послідовність дій. Такі завдання призначені для перевірки знання відомих алгоритмів.
Автор мав на меті допомогти всім зацікавленим якісно повторити свої знання з математики, щоб посібник став реальним помічником як учня, так і вчителя математики.
Автор щиро сподівається, що завдяки цьому посібнику ви не тільки досягнете бажаних результатів а й отримаєте насолоду від процесу їх одержання.
Розділ 1. Числа і вирази
- Цілі і дробові раціональні вирази
Завдання на достатність даних та завдання на порівняння величин.
У завданнях 1-4 сформульовано проблему (питання), яку потрібно розв’язати (отримати однозначну відповідь на питання), використовуючи для цього додаткові дані - твердження (1) і (2). Визначте, чи достатньо цих даних для розв’язання проблеми, І оберіть одну правильну, на вашу думку, відповідь. Саму проблему розв’язувати не обов’язково.
- Знайдіть значення виразу х2 - 4х +4.
- (х+2)3=8
- 4(х-2)=32
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Б.
- Знайдіть значення виразу a – 5b.
- 6a – 30b +18 = 0
- 10b – 2a = 6
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: В.
- Чи є число b 0 раціональним?
-
Число 2
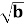 раціональне
раціональне
- Число b2 раціональне
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) – ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: А.
- Чи є число а натуральним?
- Число а + 5 натуральне
- Число а2 натуральне
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) – ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Д
У завданнях 5 – 6 порівняйте величини Х і Y та оберіть одну правильну, на вашу думку, відповідь.
- Задано вираз (а + 5) (а – 3) (а + 4) ( а – 6).
Величина Х: значення виразу при а = 0
Величина Y: значення виразу при а = 3
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: А.
-
Відомо, що
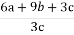 = 1.
= 1.
Величина Х: ![]() +
+ ![]() .
.
Величина Y: 5.
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: Б.
Завдання на встановлення відповідності
У завданнях 7 – 10 до кожного рядка, позначеного цифрою, доберіть один відповідник, позначений літерою.
- Установіть відповідність між значеннями числових виразів (1 – 4) і проміжками ( А- Д), яким вони належать.
-
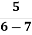 А (- ; 4 )
А (- ; 4 )
- (4 – 3) ( 7 – 6) Б ( - 8; 0
-
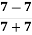 В ( -2; 1
В ( -2; 1
- (1 + 9 ) ( 5 – 8) Г ( -2; 4)
Д ( 6; 18)
Відповідь: 1- Б; 2- В; 3- Г; 4- А.
- Установіть відповідність між проміжками (1- 4), яким належать значення числових виразів (А- Д), і цими числовими виразами.
1 ( -; 5) А (3 – 2) (3+2)
2 (-8 ; 8) Б ![]()
3 (0 ; 2) В ![]()
4 (-1 ; +) Г ![]()
Д ![]()
Відповідь: 1-Г; 2-А; 3-Б; 4-В.
- Установіть відповідність між виразами (1 – 4) і тотожно рівними їм виразами (А – Д ).
1 (а – 3)2 А 9 – а2
2 (b – 3) (b + 3) Б а2 – 9
3 (2а + 1 )2 В а2 – 6а + 9
4 (а + 3) (3- а) Г 4а2 + 4а +1
Д b2 – 9
Відповідь: 1-В; 2-Д; 3-Г; 4-А.
- Установіть відповідність між виразами (1 – 4) і тотожно рівними їм виразами (А – Д ).
1 а2 – 4аb А b(2b –а)
2 аb – b2 Б а(а – 4b)
3 2b2 – аb В b(b – а)
4 аb – 2b2 Г b(а – b)
Д b(а – 2b)
Відповідь: 1- Б; 2- Г; 3- А;4- Д.
Завдання на встановлення послідовності
У завданнях 11- 12 виберіть тільки необхідні для розв’язання поставленої задачі дії і розмістіть їх у правильній послідовності. У відповідь запишіть отриману послідовність літер.
11. Як обчислити значення виразу ![]()
А До 3 додати 6.
Б Чисельник і знаменник першого дробу помножити на 2.
В Результат поділити на 6.
Г До 2 додати 5.
Д До 5 додати 2.
Е До 4 додати 5.
Є Результат поділити на 9.
Відповідь: Б, Е, В.
- Як знайти показник n у рівності ( а9 : а4)3 = аn.
А До 9 додати 4.
Б Результат поділити на 3.
В До 5 додати 3.
Г Від 9 відняти 4.
Д Від 5 відняти 3.
Е Результат помножити на 3.
Відповідь: Г, Е.
1.2 Ірраціональні вирази.
Завдання на достатність даних та завдання на порівняння величин.
У завданнях 1-4 сформульовано проблему (питання), яку потрібно розв’язати (отримати однозначну відповідь на питання), використовуючи для цього додаткові дані - твердження (1) і (2). Визначте, чи достатньо цих даних для розв’язання проблеми, І оберіть одну правильну, на вашу думку, відповідь. Саму проблему розв’язувати не обов’язково.
-
Знайдіть значення виразу 5а +
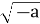
- а = 9.
- 5а = -15.
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) – ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: В.
-
Знайдіть значення виразу
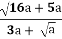
- а 0 .
- 5а = 5.
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) – ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: В.
- Знайдіть Y.
- (-y)8 = 256.
- (-у)7 = 128.
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) – ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Б.
-
Знайдіть 2
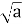 + 3
+ 3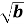
-
4а + 12
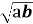 + 9b = 16.
+ 9b = 16.
- 2а + 3b = 1.
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) – ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: А.
У завданнях 5 – 6 порівняйте величини Х і Y та оберіть одну правильну, на вашу думку, відповідь.
-
Відомо, що,
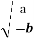 =
= 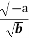 .
.
Величина Х: значення параметра а.
Величина Y: значення параметра b.
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: Б.
-
Відомо, що,
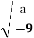 =
= 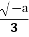 .
.
Величина Х: значення параметра а.
Величина Y: 0.
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: Г.
Завдання на встановлення відповідності
У завданнях 7 – 10 до кожного рядка, позначеного цифрою, доберіть один відповідник, позначений літерою.
- Установіть відповідність між виразами (1 – 4) і тотожно рівними їм виразами (А – Д ) при а ≥ 0.
-
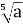 2 А а3
2 А а3
-
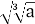 3 Б
3 Б 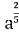
-
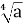 8 В а2
8 В а2
-
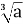 9 Г
9 Г 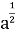
Д ![]()
Відповідь: 1- Б; 2 –Г; 3 – В; 4 – А.
- Установіть відповідність між виразами (1 – 4) і тотожно рівними їм виразами (А – Д ) при а ≥ 0.
1 ![]() А 2а
А 2а
2 ![]() Б 5
Б 5![]()
3 ![]() В
В ![]()
4 ![]() Г 5а
Г 5а
Д 2![]()
Відповідь: 1 – В; 2 – Д; 3 – А; 4 –Б.
- Установіть відповідність між властивостями чисел (1 – 4) і числами ( А –Д), які мають ці властивості.
-
Число є натуральним А
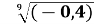 3
3
- Число є цілим,
але не є натуральним Б ![]() 2
2
- Число є раціональним,
але не є цілим В ![]() 2
2
- Число є ірраціональним
і додатним Г ![]() 5
5
Д ![]() 2
2
Відповідь: 1 – Д; 2 –Г; 3 – В; 4 – Б.
- Установіть відповідність між властивостями чисел (1 – 4) і числами ( А –Д), які мають ці властивості.
1 Число є натуральним А ![]()
2 Число є цілим,
але не є натуральним Б ![]()
3 Число є раціональним,
але не є цілим В ![]()
4 Число є ірраціональним
і від’ємним Г ![]()
Д ![]()
Відповідь: 1 – Д; 2 – А; 3 – Г; 4 – В.
Завдання на встановлення послідовності
У завданнях 11- 12 виберіть тільки необхідні для розв’язання поставленої задачі дії і розмістіть їх у правильній послідовності. У відповідь запишіть отриману послідовність літер.
-
Як знайти а у рівності
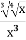 = ха
= ха
А Від n відняти 3.
Б Знайти m як добуток 3 на 4.
В Від 12 відняти 3.
Г Позначити n = ![]() .
.
Д Поділити 12 на 3.
Відповідь: Б, Г, А.
-
Як знайти показник b у рівності
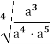 = аb
= аb
А Помножити 3 на 4. Г Позначити n = 3 – m.
Б Знайти m як суму 4 і 5. Д Поділити n на 4.
В Помножити 4 на 5. Відповідь: Б, Г, Д.
1.3 Тригонометричні вирази
Завдання на достатність даних та завдання на порівняння величин.
У завданнях 1-4 сформульовано проблему (питання), яку потрібно розв’язати (отримати однозначну відповідь на питання), використовуючи для цього додаткові дані - твердження (1) і (2). Визначте, чи достатньо цих даних для розв’язання проблеми, І оберіть одну правильну, на вашу думку, відповідь. Саму проблему розв’язувати не обов’язково.
1 . Знайдіть 10 tg α.
-
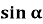 =
= 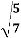
-
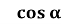 =
= 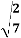
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Г.
-
Знайдіть 3 +
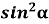 .
.
-
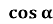 =
= 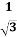
-
ctg
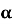 =
= 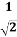
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: В.
-
Знайдіть
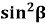 -
- 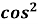 β.
β.
-
sin
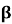 -
- 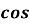 β = -0,1
β = -0,1
-
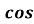 β = 0,3.
β = 0,3.
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Б.
-
Знайдіть sin
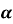 ⋅
⋅ 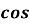 α
α
-
sin
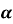 -
- 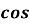
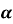 = 1,4
= 1,4
-
sin
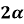 = 0,96
= 0,96
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: В.
У завданнях 5 – 6 порівняйте величини Х і Y та оберіть одну правильну, на вашу думку, відповідь.
-
Відомо, що α ϵ (
 ;
;  ).
).
Величина Х: sin ![]() .
.
Величина Y: ![]()
![]() .
.
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: А.
-
Відомо, що β ϵ (
 П).
П).
Величина Х: ![]()
![]() .
.
Величина Y: ![]() .
.
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: Б.
Завдання на встановлення відповідності
У завданнях 7 – 10 до кожного рядка, позначеного цифрою, доберіть один відповідник, позначений літерою.
- Установіть відповідність між виразами (1 – 4) і тотожно рівними їм виразами (А – Д ).
1 ![]()
![]() А
А ![]() (П+
(П+![]()
2 -![]()
![]() Б
Б ![]() (-
(-![]() )
)
3 ![]()
![]() В
В ![]() ( П -
( П -![]() )
)
4 - ![]()
![]() Г
Г ![]() (
(![]() )
)
Д ![]() (
(![]() )
)
Відповідь: 1 – Б; 2 – А ; 3-В; 4 – Г.
- Установіть відповідність між виразами (1 – 4) і тотожно рівними їм виразами (А – Д ).
-
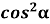 +
+ 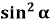 А 3 ctg
А 3 ctg
2 ![]() -
- ![]() Б
Б ![]()
3 2sin ![]() ⋅
⋅ ![]() α В 1
α В 1
4 ![]() Г
Г ![]()
Д -1
Відповідь: 1- В; 2 – Г; 3 – Б; 4 – А.
- Установіть відповідність між виразами (1 – 4) і їх числовими значеннями (А – Д).
1 sin ![]() ) А
) А ![]()
2 ![]() ( -
( - ![]() ) Б
) Б ![]()
3 tg![]() В 1
В 1
4 ctg ![]() Г -
Г - ![]()
Д ![]()
Відповідь: 1 – Г; 2 – А; 3 – В; 4 – Д.
- Установіть відповідність між виразами (1 – 4) і їх числовими значеннями (А – Д).
1 arcsin 0 A ![]()
2 arccos (-1) Б - ![]()
3 arctg 1 B 0
4 arcctg (-1) Г П Д ![]()
Відповідь: 1 – В; 2 – Г; 3- А; 4 – Б.
Завдання на встановлення послідовності
У завданнях 11- 12 виберіть тільки необхідні для розв’язання поставленої задачі дії і розмістіть їх у правильній послідовності. У відповідь запишіть отриману послідовність літер.
- Як спростити вираз tg 70°⋅ tg 20°?
А Записати відповідь: 1.
Б Подати кут 70° у вигляді різниці: 70°= 90°- 20°.
В Записати відповідь: tg2 20°.
Г Виконати перетворення за формулою tg( 90° - 20°) = ctg 20°.
Д Знайти добуток 70°і 20°.
Відповідь: Б,Г,А.
-
Як спростити вираз sin(-
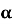 ) ⋅ tg
) ⋅ tg 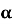 ?
?
А Записати відповідь: -![]() .
.
Б Записати відповідь: -sin ![]() .
.
В Виконати перетворення sin ![]() = - sin
= - sin ![]() .
.
Г Виразити tg ![]() через sin
через sin ![]() і
і ![]()
![]() .
.
Д Виконати перетворення sin ![]() = sin
= sin ![]() .
.
Відповідь: В,Г,А.
- Логарифмічні вирази
Завдання на достатність даних та завдання на порівняння величин.
У завданнях 1-4 сформульовано проблему (питання), яку потрібно розв’язати (отримати однозначну відповідь на питання), використовуючи для цього додаткові дані - твердження (1) і (2). Визначте, чи достатньо цих даних для розв’язання проблеми, І оберіть одну правильну, на вашу думку, відповідь. Саму проблему розв’язувати не обов’язково.
-
Знайдіть значення
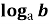
- b = а6
- b = 6а
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: А.
-
Знайдіть значення
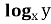 .
.
- х+у = 12
- у= 3х
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Г.
- У скільки разів число а більше за число b?
-
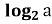 -
- 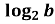 = 4
= 4
-
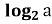 +
+ 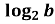 = 6
= 6
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: А.
- Знайдіть значення добутку а⋅b⋅с.
- lg a – lg b = lg c
- Lg a + lg b + lg c = 5
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Б.
У завданнях 5 – 6 порівняйте величини Х і Y та оберіть одну правильну, на вашу думку, відповідь.
- Відомо, lg( -a⋅b) = lg(-a) + Lg b.
Величина Х: значення параметра а .
Величина Y:значення параметра b .
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: Б.
-
Відомо,що
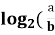 )=
)= 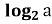 -
- 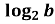 .
.
Величина Х: значення параметра а .
Величина Y:значення параметра b .
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: Г.
Завдання на встановлення відповідності
У завданнях 7 – 10 до кожного рядка, позначеного цифрою, доберіть один відповідник, позначений літерою.
- Установіть відповідність між виразами (1 – 4) і тотожно рівними їм виразами (А – Д ).
1 lg ( 100а) А 1+ lg а
2 lg а10 Б 2- lg а
3 10 lg a В 2+ lg а
4 lg(![]() ) Г 10lg а
) Г 10lg а
Д а
Відповідь: 1 – В; 2 – Г; 3- Д; 4- Б.
- Установіть відповідність між виразами (1 – 4) і їх числовими значеннями (А – Д).
1 ![]() А -1
А -1
2 ![]() Б 0
Б 0
3 ![]() В
В ![]()
4 ![]() Г 2
Г 2
Д 1
Відповідь: 1 – В; 2 – Г; 3 – Д; 4 – Б.
- Установіть відповідність між властивостями чисел (1 – 4) і числами ( А –Д), які мають ці властивості.
1 Число є натуральним А ![]()
2 Число є цілим,
І від’ємним Б ![]()
3 Число є раціональним,
але не є цілим В ![]()
4 Число є ірраціональним Г ![]()
Д ![]()
Відповідь: 1 – Б; 2 –Д; 3 – Г; 4 – В.
- Установіть відповідність між властивостями чисел (1 – 4) виразами ( А –Д), значення яких мають ці властивості при а 0, а 1.
1 Число є натуральним А ![]() )
)
2 Число є цілим,
І від’ємним Б ![]()
- Число є не цілим ,
раціональним і від’ємним В -![]()
- Число є не цілим ,
раціональним і додатним. Г ![]() )
)
Д -![]()
Відповідь: 1 –А ; 2 –Д; 3 –В ; 4 – Б.
Завдання на встановлення послідовності
У завданнях 11- 12 виберіть тільки необхідні для розв’язання поставленої задачі дії і розмістіть їх у правильній послідовності. У відповідь запишіть отриману послідовність літер.
-
Відомо, що
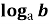 = 5 ( а 1 ,b 1). Як знайти значення виразу
= 5 ( а 1 ,b 1). Як знайти значення виразу 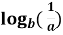
А Використати тотожність ![]() =
= ![]() .
.
Б Використати тотожність ![]() = -
= - ![]() .
.
В Використати тотожність ![]() =
= ![]() .
.
Г Використати властивість ![]() =-
=- ![]() .
.
Д Використати тотожність ![]() = -
= - ![]() .
.
Е Використати тотожність ![]() =
= ![]() .
.
Є Підставити замість виразу ![]() його значення.
його значення.
Відповідь: Б,Е,Є.
-
Відомо, що
 = 3 (0 х 1, 0 у 1). Як знайти значення виразу
= 3 (0 х 1, 0 у 1). Як знайти значення виразу 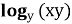 ?
?
А Використати тотожність ![]() =
= ![]() +
+ ![]() .
.
Б Використати тотожність ![]() =
= ![]() ⋅
⋅![]() .
.
В Врахувати, що ![]() = 0.
= 0.
Г Врахувати, що ![]() = 1.
= 1.
Д Використати тотожність ![]() = -
= - ![]() .
.
Е Використати тотожність ![]() =
= ![]() .
.
Є Підставити замість виразу ![]() його значення.
його значення.
Відповідь: А,Г,Е,Є.
Розділ 2.Рівняння та системи рівнянь
2.1. Цілі та дробові раціональні рівняння
Завдання на достатність даних та завдання на порівняння величин.
У завданнях 1-2 сформульовано проблему (питання), яку потрібно розв’язати (отримати однозначну відповідь на питання), використовуючи для цього додаткові дані - твердження (1) і (2). Визначте, чи достатньо цих даних для розв’язання проблеми, І оберіть одну правильну, на вашу думку, відповідь. Саму проблему розв’язувати не обов’язково.
- Знайдіть кількість коренів рівняння х2 – ах + с = 0
- С= 10
- а2 – 4с = 20
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Б.
-
Знайдіть кількість коренів рівняння
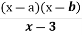 = 0
= 0
- а = 3
-
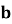 3
3
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь:Г.
У завданнях 3 – 4 порівняйте величини Х і Y та оберіть одну правильну, на вашу думку, відповідь.
-
Величина Х:корінь рівняння
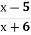 = 0
= 0
Величина Y: корінь рівняння ![]() = 0
= 0
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: А.
- Величина Х:корінь рівняння 95х = 17.
Величина Y: корінь рівняння 17 х = 95.
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: Б.
Завдання на встановлення відповідності
У завданнях 5– 7 до кожного рядка, позначеного цифрою, доберіть один відповідник, позначений літерою.
- Установіть відповідність між твердженнями (1 – 4) про кількість коренів рівнянь і цими рівняннями (А – Д ).
1 Рівняння не має коренів А 2х2 = 8
2 Рівняння має тільки один корінь Б х = х
3 Рівняння має тільки два корені В - х = -6
4 Рівняння має безліч коренів Г 2х( х – 3) (х + 4) = 0
Д ![]() =
= ![]()
Відповідь: 1 – Д; 2 – В; 3-А ; 4-Б .
- Установіть відповідність між рівняннями (1 – 4) і твердженнями про кількість їх коренів (А – Д ).
1 х2 + 5 х + 6 = 0 А Рівняння не має
коренів
2 х2 + 2х + 8 = 0 Б Рівняння має тільки
один корінь
3 х2 - 5х + 6 = 0 В Рівняння має два від’ємні
корені
4 х2 -6х +9 = 0 Г Рівняння має два додатні
корені
Д Рівняння має два
корені різних знаків
Відповідь: 1 – В; 2 – А; 3- Г ; 4- Б.
7. Установіть відповідність між твердженнями (1 – 4) про кількість розв’язків систем рівнянь і цими системами рівнянь (А – Д ).
-
Система рівнянь не має розв’язків А
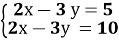
2 Система рівнянь має безліч розв’язків ![]()
3 Система рівнянь має В ![]()
тільки один розв’язок х = у =0
4 Система рівнянь має Г ![]()
тільки один розв’язок х = у = 1
![]()
Відповідь: 1 – А; 2 – Б;3 – В; 4 –Г.
Завдання на встановлення послідовності
У завданні 8- виберіть тільки необхідні для розв’язання поставленої задачі дії і розмістіть їх у правильній послідовності. У відповідь запишіть отриману послідовність літер.
8 . Як розв’язати рівняння ![]() = 0.
= 0.
А Знайти всі корені рівняння х – 2 = 0.
Б Знайти всі корені рівняння х2 – 5х + 6 = 0.
В Записати у відповідь усі корені рівняння х – 2 = 0.
Г Записати у відповідь усі корені рівняння х2 – 5х + 6 = 0.
Д Записати у відповідь усі корені рівняння х – 2 = 0, які не є коренями
рівняння х2 – 5х + 6 = 0.
Е Записати у відповідь усі корені рівняння х2 – 5х + 6 = 0, які не є коренями рівняння х – 2 = 0.
Відповідь: А, Б, Е.
2.2. Ірраціональні та тригонометричні рівняння
Завдання на достатність даних та завдання на порівняння величин.
У завданнях 1-4 сформульовано проблему (питання), яку потрібно розв’язати (отримати однозначну відповідь на питання), використовуючи для цього додаткові дані - твердження (1) і (2). Визначте, чи достатньо цих даних для розв’язання проблеми, І оберіть одну правильну, на вашу думку, відповідь. Саму проблему розв’язувати не обов’язково.
- Знайдіть значення виразу 10 + х.
-
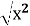 = 9
= 9
-
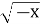 = 3
= 3
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Б.
2. Знайти значення виразу ![]()
(1) ![]() = 2.
= 2.
(2) ![]() = 2.
= 2.
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: А.
3. Знайти значення виразу 6х.
(1) tgx = 12
(2) 0 x П
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Г.
4. Знайти значення виразу х2
(1) ![]() .
.
(2) 0 x П.
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь:Д .
Завдання на встановлення відповідності
У завданнях 5– 6 до кожного рядка, позначеного цифрою, доберіть один відповідник, позначений літерою.
5. Установіть відповідність між рівняннями (1 – 4) і числами (А – Д), що є
коренями цих рівнянь.
1 ![]() =
=![]() А
А ![]()
-
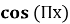 = 1 Б
= 1 Б 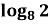
-
tg (Пх) = 1 В
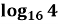
-
сtg (Пх) = 0 Г
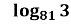
Д ![]()
Відповідь: 1- Б; 2 – А; 3 - Г; 4 – В.
6. Установіть відповідність між твердженнями (1 – 4) про кількість коренів рівнянь і цими рівняннями (А – Д),
1 Рівняння не має коренів А ![]() = (0.5х)2
= (0.5х)2
2Рівняння має тільки один корінь Б ![]() = (х – 1)2
= (х – 1)2
3 Рівняння має тільки два корені В ![]() = - х2
= - х2
4 Рівняння має безліч коренів Г ![]() = 0.22
= 0.22
Д ![]() = х2
= х2
Відповідь: 1 – В; 2 – Д; 3 - Б; 4 – Г.
Завдання на встановлення послідовності
У завданні 7 виберіть тільки необхідні для розв’язання поставленої задачі дії і розмістіть їх у правильній послідовності. У відповідь запишіть отриману послідовність літер.
7. Як розв’язати рівняння ![]() = 5.
= 5.
А Записати область допустимих значень (ОДЗ) змінної х: х – 2 ≥ 0; х ≥ 2.
Б Розв’язати рівняння х – 2 = 5.
В Розв’язати рівняння ![]() = 5.
= 5.
Г Розв’язати рівняння х – 2 = 10.
Д Серед коренів розв’язаного рівняння вибрати ті , що належать
ОДЗ.
Відповідь:А, Б,Д.
2.3. Показникові та логарифмічні рівняння
Завдання на достатність даних та завдання на порівняння величин.
У завданнях 1-2 сформульовано проблему (питання), яку потрібно розв’язати (отримати однозначну відповідь на питання), використовуючи для цього додаткові дані - твердження (1) і (2). Визначте, чи достатньо цих даних для розв’язання проблеми, І оберіть одну правильну, на вашу думку, відповідь. Саму проблему розв’язувати не обов’язково.
1. Знайдіть значення виразу а ⋅b.
(1) 3а = 81
(2) 2а = 4b
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Г.
2. Знайдіть значення виразу а + b.
(1) ![]() = 3.
= 3.
(2) ![]() = 2.
= 2.
|
А |
Б |
В |
Г |
Д |
|
Даних (1) достатньо, а даних (2) - ні |
Даних (2) достатньо, а даних (1) - ні |
І даних (1), і даних (2), взятих окремо, достатньо |
Даних (1) і (2) тільки разом достатньо |
Ні даних (1), ні даних (2) навіть разом недостатньо |
Відповідь: Г.
У завданнях 3 – 4 порівняйте величини Х і Y та оберіть одну правильну, на вашу думку, відповідь.
3. Величина Х: корінь рівняння ![]() = 3.
= 3.
Величина Y: корінь рівняння ![]() = 2.
= 2.
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: А.
4. Величина Х: корінь рівняння ![]() +
+ ![]() = 3
= 3
Величина Y: корінь рівняння ![]() = 0,5.
= 0,5.
|
А |
Б |
В |
Г |
|
Величина Х більша за величину Y |
Величина Y більша за величину Х |
Величини Х і Y рівні між собою |
Для порівняння величин Х і Y недостатньо даних |
Відповідь: В.
Завдання на встановлення відповідності
У завданнях 5 – 6 до кожного рядка, позначеного цифрою, доберіть один відповідник, позначений літерою.
- Установіть відповідність між рівняннями(1 – 4) і числовими проміжками (А – Д ), яким належать корені цих рівнянь.
1 5х = 1 А ( 0 ;7)
2 (![]() )х = 2 Б ( -1;1)
)х = 2 Б ( -1;1)
3 2х = 32 В [ - 1; 1)
4 (0. 1)х = 100 Г ( - 3; 0)
Д (- ;1 0)
Відповідь:1 – Б; 2- В; 3 – А; 4 – Г.
- Установіть відповідність між рівняннями(1 – 4) і числовими проміжками (А – Д ), яким належать корені цих рівнянь.
1 ![]() =
= ![]() А (5; 30)
А (5; 30)
2 ![]() = -3 Б ( 0; 1)
= -3 Б ( 0; 1)
3 ![]() = - 2 В ( 1; 3)
= - 2 В ( 1; 3)
4 ![]() = 7 Г ( -; -100)
= 7 Г ( -; -100)
Д ( 100; 128
Відповідь: 1 – В; 2 – А; 3 – Б; 4 – Д.
Завдання на встановлення послідовності
У завданнях 7 - 8 виберіть тільки необхідні для розв’язання поставленої задачі дії і розмістіть їх у правильній послідовності. У відповідь запишіть отриману послідовність літер.
-
Як розв’язати рівняння
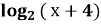 = 3.
= 3.
А Записати ОДЗ: х + 4 ≥ 0.
Б Записати ОДЗ: х + 4 0 , х - 4.
В Розв’язати рівняння х + 4 = 3.
Г Знайти всі корені рівняння ![]() = 3.
= 3.
Д Записати у відповідь тільки ті корені розв’язаного рівняння, що належать ОДЗ, або зробити висновок, що таких коренів не існує.
Відповідь: Б, Г, Д.
- Як розв’язати рівняння 3 х + 2 = 243.
А Записати ОДЗ: х + 2 0.
Б Записати число 243 у вигляді степеня числа з основою 3.
В Отриманий результат помножити на 2.
Г Від 5 відняти 2.
Д Отриманий результат записати у відповідь.
Відповідь: Б, Г, Д.
Розділ 3.Графічне розв’язування нерівностей та їх систем з двома невідомими
- Системи лінійних нерівностей та рівнянь з двома невідомими.
Раніше мова йшла про розв’язування нерівностей з двома невідомими першого степеня. Розв’язати систему кількох лінійних нерівностей з двома невідомими означає знайти таку множину ![]() пар чисел, які задовольняють кожну нерівність. Якщо
пар чисел, які задовольняють кожну нерівність. Якщо![]() і т. д. множини розв’язків кожної нерівності, то
і т. д. множини розв’язків кожної нерівності, то ![]() і т.д. є множина розв’язків системи. Геометрично множина
і т.д. є множина розв’язків системи. Геометрично множина ![]() є спільною частиною (перетин) всіх тих півплощин, які визначають кожну нерівність системи.
є спільною частиною (перетин) всіх тих півплощин, які визначають кожну нерівність системи.
Приклади
Зобразити геометрично множину ![]() розв’язків системи та записати
розв’язків системи та записати ![]() в явному вигляді за допомогою нерівностей:
в явному вигляді за допомогою нерівностей:
а) ![]()
![]() б)
б) ![]() в)
в)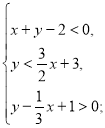 г)
г)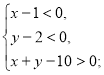 д)
д) 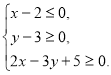
Розв’язання
а) І. Розв’яжемо обидві нерівності відносно ![]() :
:
![]()
![]() .
.
Будуємо графіки:
![]()
![]()
![]() .
.
Множиною ![]() є та частина площини, яка знаходиться одночасно вище прямої
є та частина площини, яка знаходиться одночасно вище прямої ![]() та нижче прямої
та нижче прямої ![]() (рис. 10).
(рис. 10).
ІІ. Знаходимо точку перетину прямих, для чого розв’яжемо систему 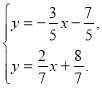 Маємо:
Маємо: ![]() . Множина
. Множина ![]() залишається системою:
залишається системою: 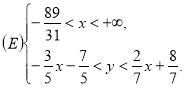
(рис. 1).
Покажемо, як цю систему можна одержати інакше. За умовою ![]()
![]() , звідси
, звідси ![]() . Із останньої нерівності випливає:
. Із останньої нерівності випливає: ![]() , або
, або ![]() . Тому шукана система, що явно описує множину
. Тому шукана система, що явно описує множину ![]() , має вигляд:
, має вигляд: 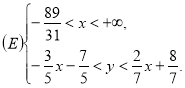
Конкретний приклад. Нехай ![]() , що становить більше
, що становить більше ![]() . Тоді
. Тоді ![]() . Це означає, що множина
. Це означає, що множина ![]() має в своєму складі пари (1, -1), (1, 0), (1, 1) і т. д., а пари (1, 2), (1, -2) і т. д. не належать до
має в своєму складі пари (1, -1), (1, 0), (1, 1) і т. д., а пари (1, 2), (1, -2) і т. д. не належать до ![]() .
.
Множину ![]() можна записати як
можна записати як ![]() , тобто
, тобто ![]() (див. рис. 10), де
(див. рис. 10), де 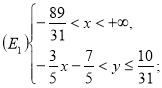
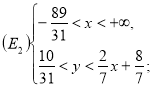
або 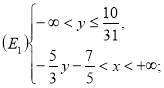
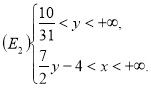
б) І. Розв’яжемо обидві нерівності відносно ![]() :
: ![]() ,
, ![]() . Будуємо графіки:
. Будуємо графіки: ![]() ,
, ![]() . Множина
. Множина ![]() ; півплощини, що відповідають кожній нерівності системи, не мають жодної спільної точки (рис. 2).
; півплощини, що відповідають кожній нерівності системи, не мають жодної спільної точки (рис. 2).
ІІ. Із того що ![]() та
та ![]() випливає:
випливає: ![]() , звідки
, звідки ![]() ,
, ![]() , що неможливо. Отже, дана система розв’язків не має,
, що неможливо. Отже, дана система розв’язків не має, ![]() .
.
в) І. Розв’яжемо кожну нерівність відносно ![]() :
: ![]() ,
, ![]() ,
, ![]() . Будуємо графіки:
. Будуємо графіки: ![]() ,
, ![]() ,
, ![]() . Знаходимо, що множина
. Знаходимо, що множина ![]() розв’язків даної системи зображується тими точками площини, які лежать всередині трикутника
розв’язків даної системи зображується тими точками площини, які лежать всередині трикутника ![]() , причому, точки сторін його не належать множині
, причому, точки сторін його не належать множині ![]() (рис. 3).
(рис. 3).
ІІ. Знаходимо координати точок ![]() перетину відповідних прямих:
перетину відповідних прямих:
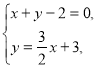
![]()
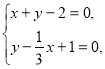
![]()
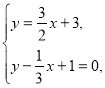
![]() .
.
Множина ![]() є об’єднанням множин
є об’єднанням множин ![]() та
та ![]() , які представлені внутрішніми точками
, які представлені внутрішніми точками ![]() і
і ![]()
![]() і записується:
і записується: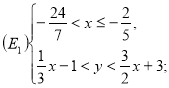
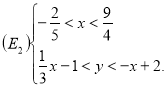
(рис. 12)
Якщо провести ![]() , то
, то ![]() , де
, де ![]() та
та ![]() є внутрішні точки відповідно
є внутрішні точки відповідно ![]() та
та ![]() :
:
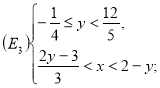
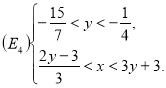
г) І. Тут маємо: ![]() ,
, ![]() ,
, ![]() . Будуємо графіки:
. Будуємо графіки: ![]() ,
, ![]() ,
, ![]() . Множина
. Множина ![]() повинна бути одночасно зліва від прямої
повинна бути одночасно зліва від прямої ![]() , нижче прямої
, нижче прямої ![]() та вище прямої
та вище прямої ![]() . Неважко помітити, що
. Неважко помітити, що ![]()
(рис. 4).
ІІ. За умовою ![]() , звідки
, звідки ![]() , або
, або ![]() . Але ж за тією самою умовою
. Але ж за тією самою умовою ![]() . Цього не може бути, система немає розв’язку, тобто
. Цього не може бути, система немає розв’язку, тобто ![]() .
.
д) Знаходимо :![]() ,
, ![]() ,
, ![]() .
.
Побудувавши графіки: ![]() ,
, ![]() ,
, ![]() , знайдемо, що множина
, знайдемо, що множина ![]() складається з одного елемента:
складається з одного елемента: ![]() . Підставивши
. Підставивши ![]() в третю нерівність, впевнюємось у тому, що
в третю нерівність, впевнюємось у тому, що ![]() є розв’язком даної системи (рис. 5).
є розв’язком даної системи (рис. 5).
- Квадратні рівняння та нерівності з двома невідомими
Розглянемо деякі випадки квадратних рівнянь та нерівностей з двома невідомими: ![]() ,
, ![]() , і т. п.,
, і т. п., ![]() ,
, ![]() тощо.
тощо.
Розв’язати таке рівняння або нерівність означає знайти таку множину ![]() пар чисел, яка б задовольняла це рівняння або нерівність.
пар чисел, яка б задовольняла це рівняння або нерівність.
Приклади
Знайти кілька розв’язків, якщо вони є, та побудувати геометрично всю множину розв’язків таких рівнянь та нерівностей:
а) ![]() ; б)
; б) ![]() ;
;
а`) ![]() ; б`)
; б`) ![]() ;
;
Розв’язання
а) Розв’яжемо рівняння відносно ![]() :
: ![]() . Надаючи
. Надаючи ![]() будь яких дійсних значень, будемо одержувати відповідні значення
будь яких дійсних значень, будемо одержувати відповідні значення ![]() . Так
. Так ![]() ,
, ![]() . Будуємо графік
. Будуємо графік ![]()
(рис. 6).
Геометрично вся множина ![]() розв’язків цього рівняння збігається з множиною точок параболи
розв’язків цього рівняння збігається з множиною точок параболи ![]() .
.
а`) Маємо ![]() . Надаючи
. Надаючи ![]() будь-яких значень, і беручи
будь-яких значень, і беручи ![]() більшим за
більшим за ![]() , дістанемо пари розв’язків цієї нерівності. Так,
, дістанемо пари розв’язків цієї нерівності. Так, ![]() ,
, ![]() .
.
Геометрично це та частина площини (див.рис. 6), яка розташована вище параболи ![]() . Друга частина площини (заштрихована горизонтальними лініями) виражає множину розв’язків нерівності
. Друга частина площини (заштрихована горизонтальними лініями) виражає множину розв’язків нерівності ![]() .
.
б) Маємо ![]() ,
, ![]() . Тут
. Тут ![]() можна надавати не будь-яких значень, а тільки ті, які задовольняють нерівність
можна надавати не будь-яких значень, а тільки ті, які задовольняють нерівність ![]() , або
, або ![]() , тобто
, тобто ![]() .
.
Наприклад, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(рис. 7).
Геометрично вся множина ![]() є множиною точок кола:
є множиною точок кола: ![]() ,
, ![]() (рис. 7).
(рис. 7).
б`) Тут маємо ![]() ,
, ![]() ,
, ![]() . Якщо надати
. Якщо надати ![]() значень із відрізка
значень із відрізка ![]() та брати
та брати ![]() таким, щоб
таким, щоб ![]() , то дістанемо пари розв’язків цієї нерівності:
, то дістанемо пари розв’язків цієї нерівності: ![]() ,
, ![]() тощо.
тощо.
Геометрично вся множина ![]() розв’язків цієї нерівності є множиною точок площини, розташованих в середині кола
розв’язків цієї нерівності є множиною точок площини, розташованих в середині кола ![]() . Множина точок, розташованих поза колом, геометрично виражає множину розв’язків нерівності
. Множина точок, розташованих поза колом, геометрично виражає множину розв’язків нерівності ![]() (рис. 7).
(рис. 7).
- Геометрична інтерпретація розв’язків нерівності
з двома невідомими
Для відповіді на запитання нагадаємо, що кожна крива другого порядку на площині, задана рівнянням ![]() , розбиває всі точки площини на три множини: а) точки що належать кривій, їх координати задовольняють рівняння
, розбиває всі точки площини на три множини: а) точки що належать кривій, їх координати задовольняють рівняння ![]() ; б) точки що знаходяться «над» кривою, їх координати задовольняють нерівність
; б) точки що знаходяться «над» кривою, їх координати задовольняють нерівність ![]() ; в) точки, що знаходяться «під» кривою, їх координати задовольняють нерівність
; в) точки, що знаходяться «під» кривою, їх координати задовольняють нерівність ![]() .
.
Приклади
-
Побудувати графік нерівності
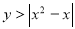 .
.
Розв’язання. Побудуємо спочатку графік функції ![]() , потім графік функції
, потім графік функції ![]() (рис. 8). Розв’язком нерівності, а отже, її графіком, є заштрихована частина площини (рис. 8).
(рис. 8). Розв’язком нерівності, а отже, її графіком, є заштрихована частина площини (рис. 8).
-
Побудувати графік нерівності
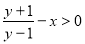 .
.
Розв’язання.
Якщо ![]() , то
, то ![]() ;
; ![]() .
.
Розглянемо три випадки:
а) ![]() , тоді
, тоді ![]() ;
;
б) ![]() , тоді
, тоді ![]() ;
;
в) ![]() , тоді
, тоді ![]() ;
;
Якщо ![]() , то
, то ![]() ;
; ![]() .
.
Знову розглянемо три випадки:
а) ![]() , тоді
, тоді ![]() ;
;
б) ![]() , тоді
, тоді ![]() ;
;
в) ![]() , тоді
, тоді ![]() ,
,
(рис. 8)
(рис. 9)
Будуємо графік функції ![]() (рис. 9). Заштрихована частина площини і буде графіком даної нерівності.
(рис. 9). Заштрихована частина площини і буде графіком даної нерівності.
Зведення нерівності до виду ![]() не завжди вдається.
не завжди вдається.
Наприклад.
-
Побудувати графік нерівності
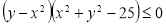 . Розв’язання. Розглянемо дві системи нерівностей:
. Розв’язання. Розглянемо дві системи нерівностей:
а) 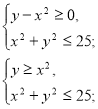 б)
б) 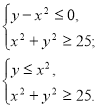
Зрозуміло, що графіком нерівності ![]() є точки площини, які лежать всередині або поза колом
є точки площини, які лежать всередині або поза колом ![]() . Враховуючи нерівності
. Враховуючи нерівності ![]() для першої і
для першої і ![]() для другої системи, будуємо графік вихідної нерівності (рис. 10).
для другої системи, будуємо графік вихідної нерівності (рис. 10).
Зауваження. Аналогічно можна було б розв’язати і приклад ![]()
![]() .
.
Зведемо до спільного знаменника в лівій частині: ![]() .
.
Розглянемо дві системи нерівностей:
а) ![]() б)
б) ![]() і т. д.
і т. д.
Розв’язуючи приклад ![]() першим способом, ми по суті застосовували метод інтервалів (для
першим способом, ми по суті застосовували метод інтервалів (для ![]() і
і ![]() ). Використаємо цей метод для розв’язування нерівностей, коли змінні знаходяться під знаком модуля.
). Використаємо цей метод для розв’язування нерівностей, коли змінні знаходяться під знаком модуля.
(рис. 10)
(рис. 11)
-
Побудувати графік нерівності
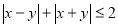 .
.
Розв’язання. Знайдемо нулі функції ![]() , або
, або ![]() ;
; ![]() , або
, або ![]() . Ці дві прямі розбивають площину на чотири області (які відіграють роль інтервалів). У кожній з цих областей беремо контрольну точку і визначаємо знаки підмодульних виразів.
. Ці дві прямі розбивають площину на чотири області (які відіграють роль інтервалів). У кожній з цих областей беремо контрольну точку і визначаємо знаки підмодульних виразів.
а) Для першої області ![]() ,
, ![]() , тоді
, тоді ![]()
![]()
![]() ;
;
б) для другої області ![]() ,
, ![]() , тоді
, тоді ![]() ;
; ![]() ;
; ![]() ;
;
в) для третьої області ![]() ,
, ![]() , тоді
, тоді ![]() ;
; ![]()
![]() ;
;
г) для четвертої області ![]() ,
, ![]() , тоді
, тоді ![]() ;
; ![]() ;
; ![]() .
.
Графіком нерівності є квадрат (рис. 11).
-
Побудувати графік нерівності
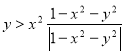 .
.
Розв’язання. Розглянемо два випадки:
а) ![]() , або
, або ![]() , тоді
, тоді ![]() ;
;
б) ![]() , або
, або ![]() , тоді
, тоді ![]() .
.
Графік нерівності зображено на рисунку 12. Бувають випадки, коли для розв’язування нерівностей з модулями не раціонально використовувати метод інтервалів.
-
Побудувати графік нерівності
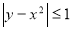 .
.
Розв’язання. Запишемо подвійну нерівність ![]() ;
; ![]() , звідки:
, звідки: 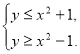 .
.
(рис. 13)
Розглянемо другий спосіб застосування методу інтервалів.
-
Побудувати графік нерівності
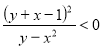 .
.
Розв’язання. Ліва частина нерівності є функція двох змінних: ![]() ;
; ![]() ,
, ![]() , якщо
, якщо ![]() .
.
Лінії ![]() і
і ![]() розбивають всю площину на дві області, у кожній з яких
розбивають всю площину на дві області, у кожній з яких ![]() зберігає знак. Щоб встановити цей знак, беремо контрольні точки (рис. 14).
зберігає знак. Щоб встановити цей знак, беремо контрольні точки (рис. 14).
-
Побудувати графік нерівності
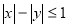 .
.
Розв’язання. Запишемо ![]() , тоді
, тоді ![]() . Функція
. Функція ![]() визначена для всіх
визначена для всіх ![]() і
і ![]() і дорівнює нулю, коли
і дорівнює нулю, коли ![]() . Легко встановити що при переході
. Легко встановити що при переході ![]() частини графіка функції, які відповідають від’ємним значенням
частини графіка функції, які відповідають від’ємним значенням ![]() , відкликаються, а ті, що лишилися , відображаються симетрично відносно осі
, відкликаються, а ті, що лишилися , відображаються симетрично відносно осі ![]() (чому?). Будуємо графік рівності
(чому?). Будуємо графік рівності ![]() . Записуємо ланцюжок: а)
. Записуємо ланцюжок: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() (рис. 15).
(рис. 15).
Розглянемо обернену задачу.
За виглядом графіків, зображених на рисунках 16, 17, 18, записати нерівності .
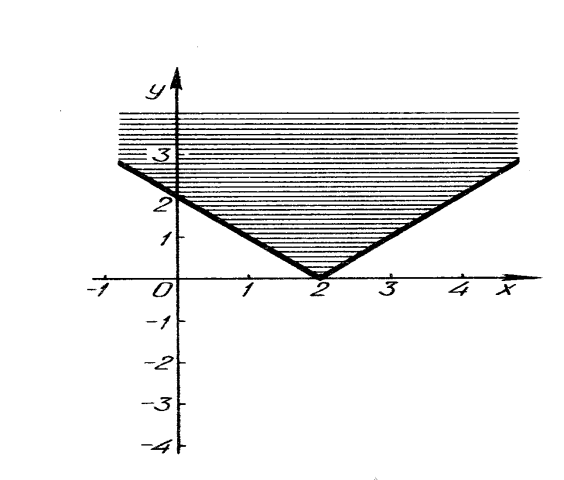
- За рисунком 16 записати нерівність.
Розв’язання. Аналізуючи рисунок 16, бачимо, що заштрихована частина площини обмежена графіком функції ![]() . Множину точок що розміщені над графіком функції
. Множину точок що розміщені над графіком функції ![]() , і точок, які належать цьому графіку, можна записати у вигляді нерівності
, і точок, які належать цьому графіку, можна записати у вигляді нерівності ![]() .
.
- За рисунком 17 записати нерівність.
Розв’язання. Спостерігаючи положення прямих, які обмежують заштрихований квадрат, записуємо їх рівняння: ![]() ;
; ![]() ;
; ![]() ;
; ![]() . У кожному координатному куті матимемо відповідну нерівність:
. У кожному координатному куті матимемо відповідну нерівність:
якщо ![]() і
і ![]() , то
, то ![]() , або
, або ![]() ,
,
якщо ![]() і
і ![]() , то
, то ![]() , або
, або ![]() ,
,
якщо ![]() і
і ![]() , то
, то ![]() , або
, або ![]() ,
,
якщо ![]() і
і ![]() , то
, то ![]() , або
, або ![]() .
.
Робимо висновок. Квадрат, обмежений прямими: ![]() ,
, ![]() ,
, ![]() ,
, ![]() є графіком нерівності
є графіком нерівності ![]() .
.
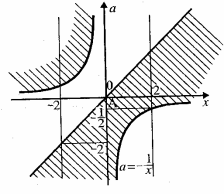
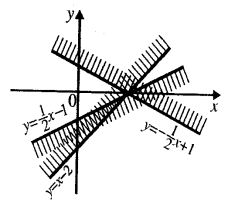
11. За рисунком 18 записати нерівність.
Розв’язання. Гіпербола, зображена на рисунку 18, записується рівнянням ![]() . Якщо
. Якщо ![]() , то
, то ![]() , що рівносильно нерівності
, що рівносильно нерівності ![]() . Крім того, нерівності
. Крім того, нерівності ![]() задовольняють також координати точок осі
задовольняють також координати точок осі ![]() . Отже, графік ,зображений на рисунку 18, записується нерівністю
. Отже, графік ,зображений на рисунку 18, записується нерівністю ![]() .
.
3.4. Графічні методи розв’язування рівнянь та нерівностей з параметрами
1.1 При яких ![]() система нерівностей
система нерівностей ![]() має розв’язок?
має розв’язок?
Розв’язання. Якщо межі півплощин, які задають нерівності системи, перетинаються, то дана система має розв’язки.
Очевидно, що ![]() не підходить. Якщо
не підходить. Якщо ![]() , то рівняння меж півплощин перепишемо в такому вигляді:
, то рівняння меж півплощин перепишемо в такому вигляді: ![]() і
і ![]() . Ці прямі перетинаються, якщо
. Ці прямі перетинаються, якщо ![]() , тобто
, тобто ![]() і
і ![]() .
.
Зрозуміло, що розв’язуваня не завершене, адже паралельність меж ще не озхначає, що вихідна система не має розв’язків. Тому необхідно розглянути випадки ![]() і
і ![]() . Якщо
. Якщо ![]() , то межі збігаються, і, очевидно, що система розв’язків не має (нерівності системі задають різні півплощини).
, то межі збігаються, і, очевидно, що система розв’язків не має (нерівності системі задають різні півплощини).
Якщо ![]() , то маємо:
, то маємо: ![]() Ця система також розв’язків не має.
Ця система також розв’язків не має.
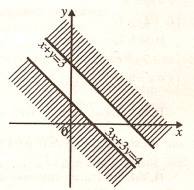 Отже,
Отже, ![]() не підходить.
не підходить.
Відповідь. ![]() і
і ![]() .
.
рис. 1.1
2.1
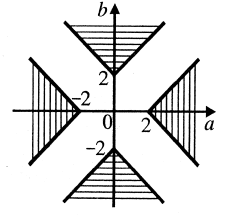
Знайти всі значення ![]() , при яких будь-який розв’язок нерівності
, при яких будь-який розв’язок нерівності ![]() за модулем не більший від 2.
за модулем не більший від 2.
Розв’язання. Перепишемо дану нерівність у такому вигляді: ![]() .
.
Графіки рівнянь ![]() й
й ![]() розбивають координатну площину
розбивають координатну площину ![]() на чотири області.(рис. 2.1).
на чотири області.(рис. 2.1).
 Тепер, якщо при деякому фіксованому значенні
Тепер, якщо при деякому фіксованому значенні ![]()
пряма ![]() в перетині з отриманою областю дає лише точки, абсциси яких задовольняють умову
в перетині з отриманою областю дає лише точки, абсциси яких задовольняють умову
рис 2.1
![]() , то
, то ![]() - одне із шуканих значень параметра. Тоді очевидно що всі
- одне із шуканих значень параметра. Тоді очевидно що всі ![]() з відрізка АВ складають
з відрізка АВ складають
Відповідь: ![]() .
.
3.1
Розв’язати нерівність ![]() .
.
Розв’язання. Наступна сукупність двох систем рівносильна заданій нерівності: ![]() або
або 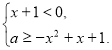
При об’єднанні графічних образів кожної із цих систем слід врахувати, що пряма ![]() дотика ється до параболи
дотика ється до параболи ![]() у точці (-1: 1).
у точці (-1: 1).
Отже на рис. 3.1 зображено всі розв’язки вихідної нерівності. Горизонтальні прямі, що перетинають цю множину, перетинають її по відрізку ( за винятком однієї прямої ![]() ).
).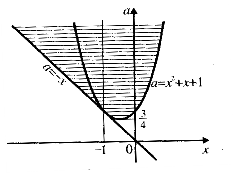 Очевидно, що абсциси всіх точок цього Рис 3.1 відрізка і будуть розв’язками даної нерівності. Для отримання відповіді залишилося виразити
Очевидно, що абсциси всіх точок цього Рис 3.1 відрізка і будуть розв’язками даної нерівності. Для отримання відповіді залишилося виразити ![]() через
через ![]() у рівнянні
у рівнянні ![]() . Якщо
. Якщо ![]() , то маємо
, то маємо ![]() .
.
4.1
Розв’язком нерівності з двома зміними ![]() та
та ![]() називають впорядковану пару змінних (
називають впорядковану пару змінних (![]() ;
; ![]() ), яка перетворює нерівність у правильну числову.
), яка перетворює нерівність у правильну числову.
Графіком нерівності з двома змінними називають множину точок координатної площини, координати яких є розв’язком нерівності.
Приклад: побудувати графік нерівності ![]() .
.
-
область визначення виразу
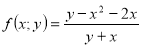
![]() 2)нулі виразу
2)нулі виразу ![]() .
.
3)Зобразимо область визначення і нулі виразу ![]() на координатній площині. Визначимо знак виразу на кожній з отриманих областей.
на координатній площині. Визначимо знак виразу на кожній з отриманих областей.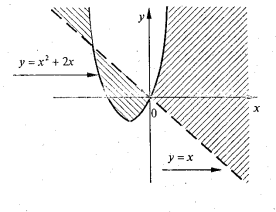 Виділимо штриховою лінією ті області, координати точок яких задовольняють дану нерівність
Виділимо штриховою лінією ті області, координати точок яких задовольняють дану нерівність
рис 4.1
5.1При яких значеннях параметра ![]() нерівність
нерівність ![]() виконується при всіх
виконується при всіх ![]() ?
?
Побудуємо графік нерівності в системі координат ![]()
![]() . Для цього визначимо:
. Для цього визначимо:
-
ОДЗ:
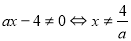 ;
;
-
нулі виразу
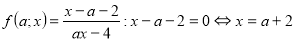 .
.
Таким чином , дістаємо графік:
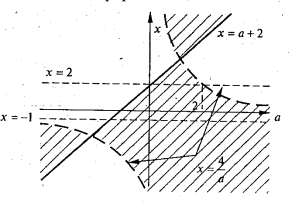
рис 5.1
З графіка нерівності знаходимо відповідь : ![]() .
.
6.1
При всіх значеннях пареметра ![]() розв’язати нерівність
розв’язати нерівність ![]() .
.
-
ОДЗ
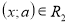 ;
;
-
Прямі
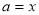 і
і 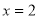 розбивають координатну площину
розбивають координатну площину 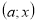 на 4 області. На кожній з них спростимо дану нерівність і побудуємо її графік.
на 4 області. На кожній з них спростимо дану нерівність і побудуємо її графік.
|
Область |
1 |
2 |
3 |
4 |
|
Нерівність |
|
|
|
|
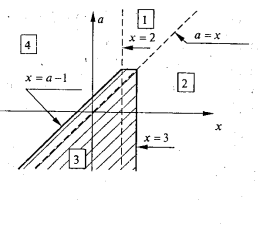
рис. 6.1
Відповідь. При ![]() ; при
; при ![]() .
.
7.1
На координатній площині зобразити множину пар ![]() , для кожної з яких рівняння
, для кожної з яких рівняння ![]() має чотири різних дійсних корені.
має чотири різних дійсних корені.
 Розв’язання.
Розв’язання. ![]() і
і ![]() - дискримінанти квадратних тричленів, що розміщені відповідно в першій і другій дужках. Для виконання умови задачі необхідно
- дискримінанти квадратних тричленів, що розміщені відповідно в першій і другій дужках. Для виконання умови задачі необхідно  тобто
тобто 
На координатній площині ![]() неважко зобразити розв’язок останньої системи (рис 7.1). рис. 7.1 Але помилково вважати отриману множину точок шуканою відповіддю. Ми не вказуватимемо відразу на помилку, хоча, ймовірно, читач сам може це зробити.
неважко зобразити розв’язок останньої системи (рис 7.1). рис. 7.1 Але помилково вважати отриману множину точок шуканою відповіддю. Ми не вказуватимемо відразу на помилку, хоча, ймовірно, читач сам може це зробити.
Розв’язування цього прикладу проходить за такою схемою. Визначаємо сукупність рівносильну даному рівнянню (системі). Потім окремо знаходимо кількість розв’язків кожного рівняння (системи) сукупності. Імовірність появи помилки зростає на останньому етапі, коли визначається загальна кількість розв’язків вихідного рівняння (системи). Причина – «механічне» об’єднання раніше отриманих розв’язків. Так немає жодних гарантій, що при певних значеннях параметрів розв’язки не збігаються.
Оскільки добуток коренів квадратних тричленів дорівнює 1 (нагадаємо, що існування таких коренів визначено умовами ![]() і
і ![]() ), то якщо один із коренів першого тричлена збігається з яким-небудь коренем другого, тоді обов’язково збігатимуться й інші корені. Таким чином, збіг яких-небудь коренів призводить до необхідності виконання рівності
), то якщо один із коренів першого тричлена збігається з яким-небудь коренем другого, тоді обов’язково збігатимуться й інші корені. Таким чином, збіг яких-небудь коренів призводить до необхідності виконання рівності ![]() , тобто
, тобто ![]() . Отже, з отриманої множини точок (рис. 7.1) потрібно виключити промені
. Отже, з отриманої множини точок (рис. 7.1) потрібно виключити промені ![]() і
і ![]() осі абсцис.
осі абсцис.
8.1
При яких ![]() система нерівностей
система нерівностей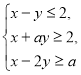 має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання. Кожна з нерівностей системи задає півплощину разом з границею на координатній площині ![]() . Якщо які-небудь дві із границь паралельні або збігаються, то очевидно, що система не може мати єдиного розв’язку. Тоді перетин розв’язків будь-яких двох нерівностей повинен задавати область, обмежену кутом (включати границю).Отже, якщо границя третьої півплощини не пройде через точку перетину двох інших границь, то система також не може мати єдиного розв’язку (розв’язків буде нескінченна кількість або жодного). Тоді всі три границі повинні проходити через одну точку. Щоправда, ця умова ще не гарантує єдиності розв’язку, а, отже, вона є необхідною.
. Якщо які-небудь дві із границь паралельні або збігаються, то очевидно, що система не може мати єдиного розв’язку. Тоді перетин розв’язків будь-яких двох нерівностей повинен задавати область, обмежену кутом (включати границю).Отже, якщо границя третьої півплощини не пройде через точку перетину двох інших границь, то система також не може мати єдиного розв’язку (розв’язків буде нескінченна кількість або жодного). Тоді всі три границі повинні проходити через одну точку. Щоправда, ця умова ще не гарантує єдиності розв’язку, а, отже, вона є необхідною.
Таким чином, система 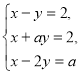 повинна мати розв’язки.
повинна мати розв’язки.
Із першого і третього рівнянь системи встановлюємо, що ![]() ,
, ![]() . Підставивши ці значення у друге рівняння, знайдемо умови, за яких система рівнянь має розв’язки. Отримуємо
. Підставивши ці значення у друге рівняння, знайдемо умови, за яких система рівнянь має розв’язки. Отримуємо ![]() . Звідси
. Звідси ![]() або
або ![]() . Серед цих значень і міститься відповідь.
. Серед цих значень і міститься відповідь.
Якщо ![]() , то
, то 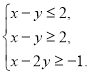
 Оскільки границі півплощин, які задають перші дві нерівності цієї системи, збігаються, то, як зазначалося вище, ця система не може мати єдиного розв’язку.
Оскільки границі півплощин, які задають перші дві нерівності цієї системи, збігаються, то, як зазначалося вище, ця система не може мати єдиного розв’язку.
Якщо ![]() , то запишемо
, то запишемо 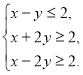
Зобразивши розв’язки кожної нерівності системи (рис. 8.1), встановлюємо, що вони мають тільки одну спільну точку.
рис. 8.1 Відповідь. ![]()
Список використаної літератури
-
Колесник Б.М.Алгебраїчні задачі на дослідження. Київ,
«Радянська школа», 1971. -
Лобанова Л.В., Фінкельштейн Л.П. Вибрані задачі елементарної
математики. Київ, «Вища школа», 1989. -
Конфорович А.Г. Колумби математики. Київ, «Радянська школа».
1982. -
Зоря А.С., Кіро С.М. Про математику І математиків. Київ,
«Радянська школа», 1981. -
Шунда Н.М. Функції та їх графіки. Київ, «Радянська школа»,
1976. - Бевз Г.П. Довідник з математики. Київ, «Радянська школа», 1981.
-
Віленкін Н.Я. Функції в природі і техніці. Москва, «Освіта»,
1978. -
Коваленко В.Г., Кривошеєв В.Я., Старосєльцева О.В, Алгебра, 9.
Експериментальний навчальний посібник для 9 класу шкіл з
поглибленим вивченням математики і спеціалізованих шкіл
фізико-математичного профілю. Допущено міністерством освіти
України. 2-ге видання. Київ, «Освіта», 1996. -
Бевз Г.П. Методика розв'язування алгебраїчних задач. Київ,
«Радянська школа», 1975.
10. Возняк Г.М., Маланюк М.П. Взаємозв'язок теорії з практикою в процесі вивчення математики. Київ, «Радянська школа», 1989.
11. Гайштут О.П., Литвиненко Г.М. Розв'язування алгебраїчних задач. Київ, «Радянська школа», 1999.
12. Захарійченко Ю.О. , Школьний О.В. , Захарійченко Л. І. , Школьна О.В.
Повний курс математики в тестах. Харків, «Ранок», 2013.
Додатки
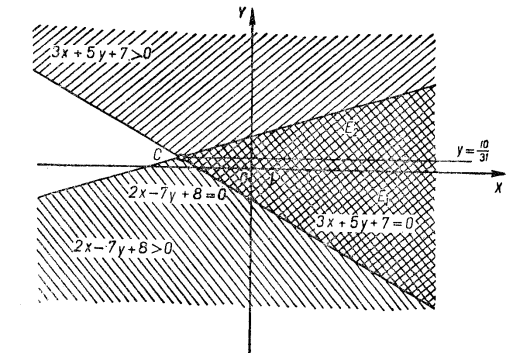
Рис.1
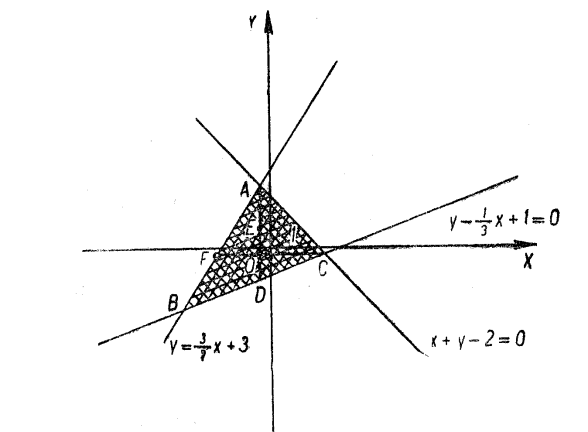
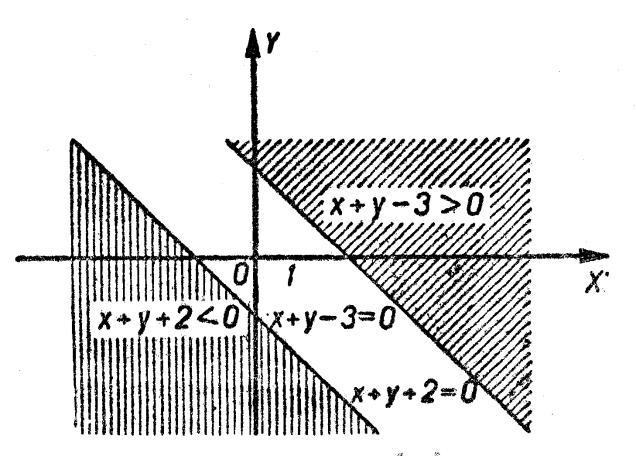 рис.2
рис.2
рис.3
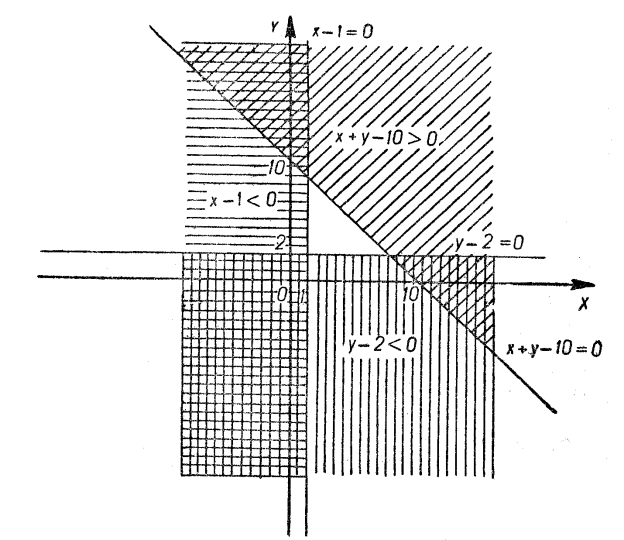 рис.4
рис.4
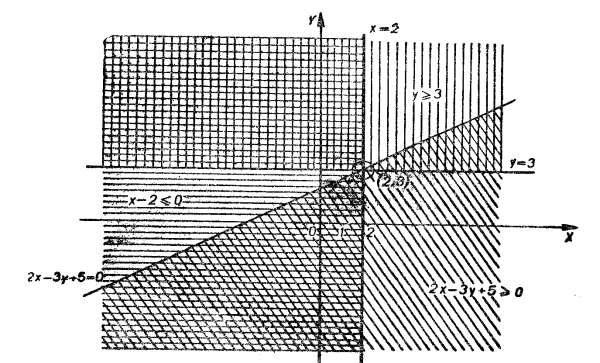 рис.5
рис.5
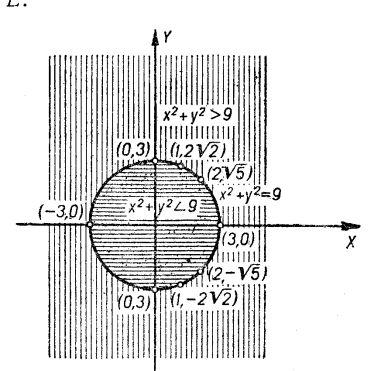
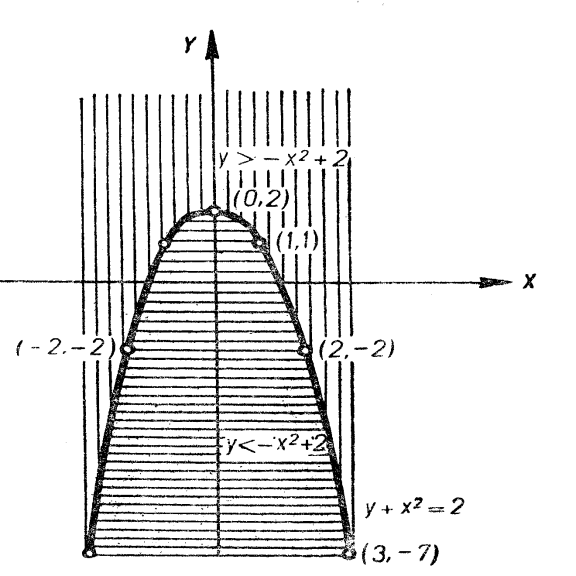 рис.6
рис.6
Рис.7
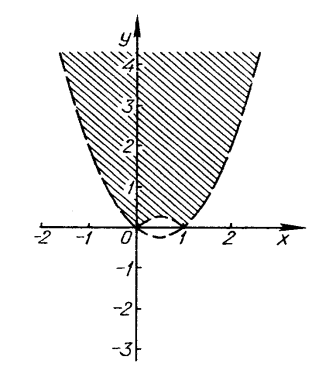
Рис.8
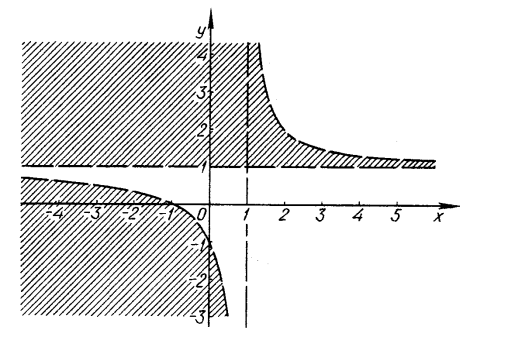
рис.9
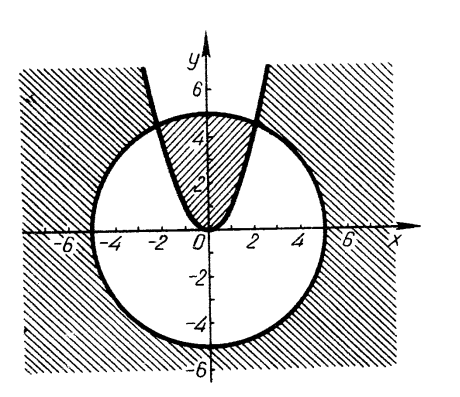
рис. 10
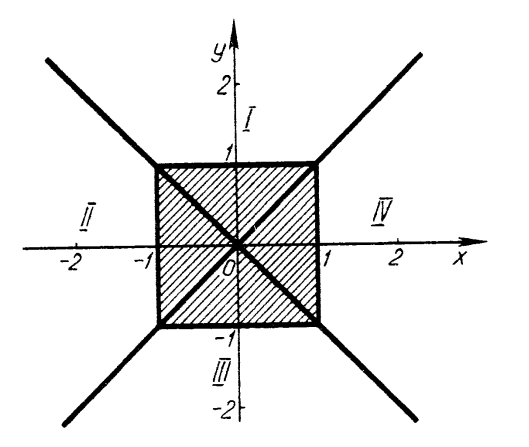
рис. 11
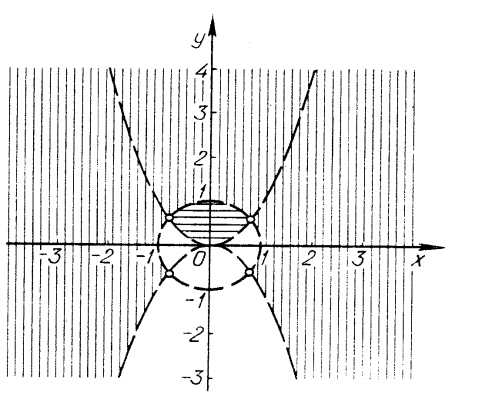
рис. 12
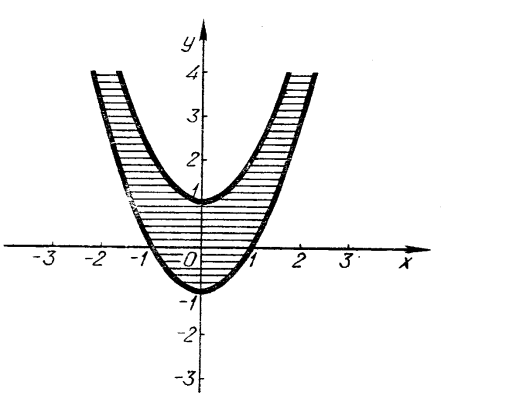
рис. 13
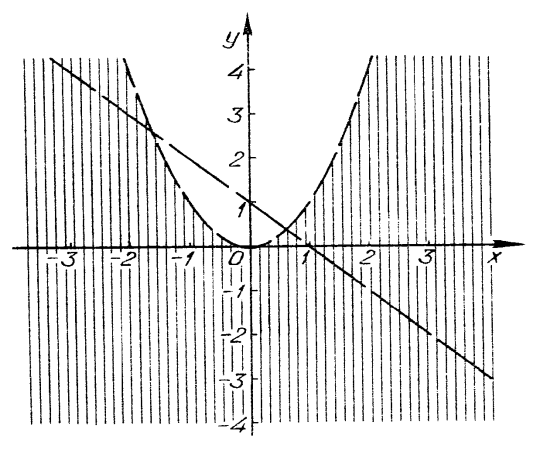
рис.14
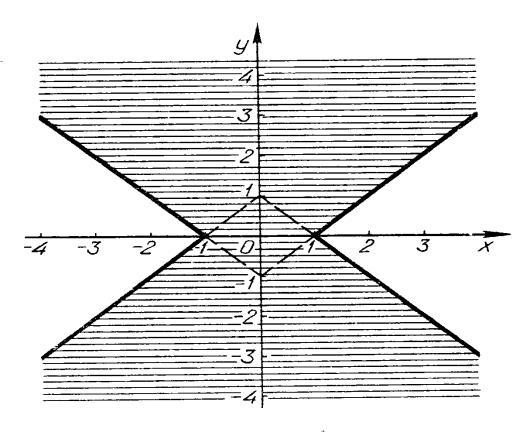
рис.15
В
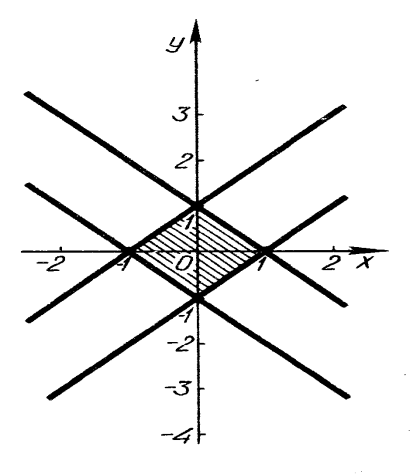 рис.16
рис.16
рис.17
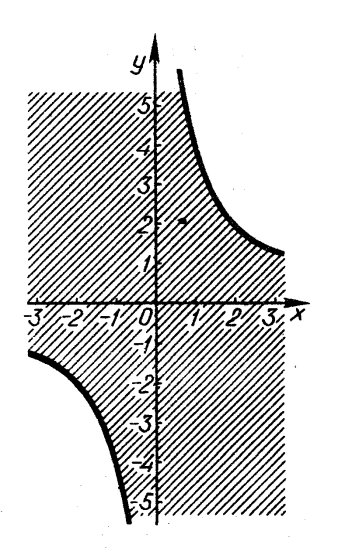
рис.18
1

про публікацію авторської розробки
Додати розробку