Матеріал до уроків підготовки до НМТ з математики

Матеріал до уроків підготовки до НМТ з математики

Хочу поділитися цікавими практико орієнтованими задачами, які можна використати під час підготовки до іспитів як в 11 так і в 9 класах. Задачу про квіти можна пропонувати 6-класникам під час вивчення теми «НСД кількох натуральних чисел», а також 7-класникам, коли вивчатимуть на уроці геометрії аксіому вимірювання відрізків. Задачу про числа можна розв’язувати в 9 класі під час вивчення теми «Числові послідовності».

Задача про квіти.

На сімейній раді вирішили створити квіткову грядку з розмірами 210 см на 140 см. Грядка буде засаджена тюльпанами через рівні проміжки по периметру. Відстань між сусідніми тюльпанами повинна бути якомога ширшою, по одному тюльпану в кожному кутку грядки, а також посередині довшої сторони грядки.

Менший прямокутник позначений всередині грядки. Нарциси будуть  висаджені  по кутах і з інтервалом 10 см по периметру цього прямокутника. Кожен нарцис буде знаходитись на відстані 25 см від найближчого краю грядки.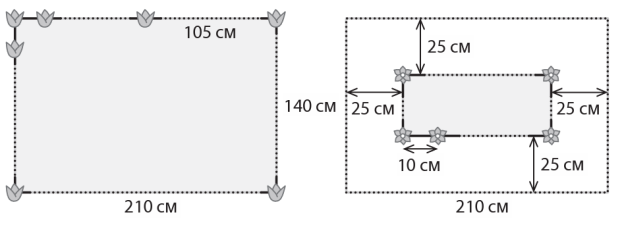

1. Обчисліть відстань у см між сусідніми тюльпанами.

2. Визначте, скільки нарцисів буде висаджено.

Розмірами рослин знехтуйте.

Задача про числа

На екрані комп'ютера з'являються два числа - синього та червоного кольору. На початку обидва числа однакові. При кожному звуковому сигналі обидва числа збільшуються одночасно. Число в синьому полі завжди збільшується на 6. Приріст числа в червоному полі регулярно чергується - одного разу число збільшується на 3, при наступному сигналі на 5, потім знову на 3, на 5, на 3, на 5, на 3 і т.д.

 У якийсь момент на екрані в синьому полі з'являється число 500, а в червоному полі - число 400.

1. Визначте, яке число знаходиться у синьому полі на початку.

2.Визначте, на скільки збільшиться число у синьому полі, якщо число у червоному полі збільшилось на 123.

3. Визначте число у червоному полі в той момент, коли воно на 444 менше за число у синьому полі.

Розв’язання задачі про квіти.

1. Відстань між тюльпанами має бути такою, щоб 105 см і 140 см ділилися на неї без остачі, при чому, за умовою задачі це має бути найбільша з усіх можливих відстаней. Отже необхідно знайти НСД (105 і 140).

105 = 3*5*7, 140 = 2*2*5*7.  НСД (105 і 140) = 5*7 = 35.

Відстань між сусідніми тюльпанами 35 см.

2. Зясуємо розміри меншого прямокутника.

Довжина: 210 – 2*25 = 160 (см).

Ширина:   140 – 2*25 = 90 (см).

Отже по довжині прямокутника буде висаджено 160 : 10 +1 =17 (нарцисів).

По ширині буде висаджено 90 : 10 +1 = 10 (нарцисів). Але нарциси, які будуть висаджені в кутах прямокутника, треба врахувати або лише в кількість квітів, висаджених по довжині, або лише в кількість квітів, висаджених по ширині прямокутника. Нехай ми врахуємо ці квіти по довжині, тоді по ширині будемо мати 10 – 2 = 8 (нарцисів). Тому всього буде висаджено 2*(17 + 8) = 50 (нарцисів).

Кількість висаджених нарцисів 50 штук.

Відповідь: 35см; 50 нарцисів.

Розв’язання задачі про числа

1.Ряд чисел в синьому полі складає арифметичну прогресію, перший член якої х, а різницею є число 6. n-й член прогресії дорівнює 500. За формулою n-го члена маємо рівняння

500 = х + (n - 1)*6,

 х = 506 - 6 n.

Число, яке з’явилося в червоному полі, 400. Воно могло з’явитися тільки після приросту на 5, тобто після парної кількості приростів. Кожна пара приростів збільшує попереднє число на 8. Такий результат був би, якщо б постійний приріст був 4. Тому математичною моделлю даної ситуації є арифметична прогресія з першим членом х, різницею 4 і  n-им членом 400.  За формулою n-го члена маємо рівняння

400 = х + (n - 1)*4,

Х = 404 – 4n.

За умовою задачі на початку обидва числа були однакові, отже

  506 - 6 n = 404 – 4n,

  102 = 2n,

   n = 51.

Тоді х = 506 – 6*51 = 200 – число, яке стояло в синьому полі на початку.

         2. Початкове число могло збільшитися на 123 тільки після непарної кількості сигналів. Тоді після передостаннього сигнала число було збільшене на 120. Оскільки кожна пара сигналів збільшувала попереднє число на 8, то 120:8=15. Отже пролунав 15*2+1 = 31 сигнал.

Тому число в синьому полі збільшилось на 31*6 = 186.

              3. Кожна пара сигналів збільшує число у синьому полі на 12, а у червоному полі на 8, тому різниця між синім і червоним числами після кожної пари сигналів кратна числу 4. Тому 444:4=111, тобто різниця між синім і червоним числами дорівнює 444 після 111 пар игналів. 111*8=888, отже 200 + 888 = 1080 – шукане число.

               Відповідь: 1. 200;   2. 186;   3. 1080.