Матеріали до уроків "Історичні задачі на уроках математики"

Про матеріал

Задачі країн Стародавнього світу(Єгипту,Вавилону,Індії та інших ),країн Середньовіччя.Цими задачами можна зацікавити учнів на уроках.

Перегляд файлу

5 клас

Тема: Натуральні числа. Додавання і віднімання натуральних чисел.

Задача Діофанта.

Знайти три числа, які при попарному додаванні дають в сумі 20, 30,40. Відповідь 5, 15, 25.

Задача А. М. Толстого

Продавець продає шапку за 10 руб. Підходить покупець, міряє, хоче взяти, але в нього є тільки 25руб. Продавець відсилає хлопчика до сусідки розміняти. Хлопчик приносить 10+10+5, продавець дає шапку і 15 руб здачі. Через деякий час сусідка каже, що 25 руб фальшиві і вимагає грошей назад. Продавець віддає. На скільки обманули продавця?

Задача Метродора.

Раз мул ішов з ослицею шляхом,

Обоє опаковані вином.

Під тягарем ослиця застогнала,

Та мул, якого від коня вона за сина мала,

Питає: «Мамо, що це за причина,

Що заскиглила ти, як молода дівчина?»

Вона відмовила, що потяжко їй двигать:

«Еге, хотіла б ти ще як дівчина плигать?

Я більше двигаю, й мені дуже гірко;

Якби від тебе взяв одно, то мав би вдвоє стільки,

А якби ти одно та віддала мені,

То мали б ми обоє по рівні»

Хто хоче тії числа відгадати,

Не треба пальців обох рук зачисляти

Мул ніс 7 мішків, ослиця 5.

Задача Алкуїна.

Собака женеться за кроликом, який знаходиться в 150 футах від неї. Вона робить стрибок на 9 футів щоразу, коли кролик стрибає на 7 футів. Скільки стрибків має зробити собака, щоб наздогнати кролика?

75 стрибків.

5. Задача із Бахшалійського рукопису (Індія).

Знайти число, яке при додаванні 5 або відніманні 11 перетворюється в повний квадрат.

6. Старовинна китайська задача.

У клітці знаходяться фазани та кролики, - у них всього 7 голів і 20 лап. Скільки в клітці фазанів і скільки кролів?

Відповідь: 3 кролики і 4 фазани.

Тема. Множення і ділення натуральних чисел

1. Задача Л.Ф.Магніцького.

В одній добі 24 години, а в році 365 днів. Якщо хочеш знати, скільки годин в році або тижні, а в 1000 діб, то помнож.

Тема: Дробові числа

1.Задача із «Арифметики» Магніцького.

Хтось залишив в спадок дружині, дочці і трьом синам 48000 рублів і заповів дружині всієї суми, а кожному з синів у 2 рази більше, ніж дочці. Скільки

одержав кожен спадкоємець?

2.Задача із « Курсу математики» Ж. Озанама.

Троє хочуть купити будинок за 24000 ліврів. Вони домовились, що перший дасть половину, другий - одну третину, а третій - решту. Скільки дасть кожен?

3.Задача Герона Александрійського.

Басейн об'ємом 12 кубічних одиниць одержує воду через дві труби, із яких одна дає кожної години кубічну одиницю, а друга 4 кубічних одиниці. За який час наповниться басейн при спільній роботі обох труб?

4. Задача із книги Івана Бутлера «Цікаві і веселі задачі і загадки».

Написати сто без нулів:

а) С (в латинській нумерації);

б) .

6 клас

Тема: Подільність чисел.

1. Задача Блеза Паскаля.

Загальна ознака подільності чисел.

Натуральне число а ділиться на число в тоді і тільки тоді, коли на нього ділиться сума добутків кожної цифри даного числа на остачу від ділення на в

відповідних цифр розрядних одиниць.

2. Задача Гольдбаха.

Будь-яке непарне число, більше за 5, можна представити у вигляді суми трьох простих чисел. Перевірте це на прикладі кількох двозначних чисел.

3. Задача із книги Баше де Мезирака.

Задумай парне число і помнож його на 3, половину отриманого добутку помнож знову на 3. Скільки дев’яток містить отримане число?

4. Задача із «Арифметики» Ібн - Сіни (Авіценни).

Якщо число, будучи поділеним на 9, дає в остачі 1 або 8, то квадрат його, поділений на 9, дає в остачі 1.

Перевірити властивість для кількох чисел.

5. Стародавня французька задача.

Жінка несла на ринок корзину яєць. Прохожий випадково штовхнув жінку, корзина впала, яйце розбилось:

- Скільки яєць було в корзині?

- Точно не пам’ятаю. Але знаю, що коли я виймала з корзини по 2, по 3, по 4, по 5, або по 6 яєць, то в корзині залишилось 1 яйце, а коли я виймала по 7, то нічого не залишилось. Скільки яєць було в корзині?

Тема: Звичайні дроби.

1. Древньоєгипетська задача.

У пастуха, який вів 70 биків, запитали: «Яку частину биків своєї численної череди ти ведеш?» Він відповів: «Я веду дві третини від третини худоби.» Скільки биків було у всій череді?

Нехай у череді було х биків

*=70,

x=70,

x=70 : ,

x = 315

Відповідь: 315 биків. .

2.3адача вірменського математика Ананія Ширакаці (середина VII ст.)

У Афінах була водойма з трьома трубами. Перша могла наповнити водойму за 1 год., друга - за 2, третя за 3. За яку частину години всі три труби разом могли наповнити водойму?

1 + + = 1 (частин водойми) - наповнять 3 труби за 1 год.

Відповідь: за год.

3. Задача Л. М. Толстого (ХІХст.)

Артіль косарів мала скосити дві луки, з яких перша вдвічі більша за другу. Половину дня всі косарі косили першу луку. Після обіду артіль розділилась на дві рівні групи. Перша група залишилася на першій луці і косила її до вечора. Друга група косила до вечора меншу луку, але на ній залишилося ділянка, яку наступного дня один косар викосив за день. Скільки косарів було в артілі. Якщо більшу луку косила півдня вся артіль і півдня пів артілі, то за півдня пів артілі скосило луки.

Отже, на малій луці залишилося не скошено частини, яку один

косар викосив за день. Але першого дня було скошено 1 + , тому косарів

було : = 8.

Відповідь: 8 косарів.

4. Із папірусу Ахмеса.

Перевірити:

б);

в)

г)

5. Із «Математики в дев'яти книгах».

Дика качка від південного моря до північного летить 7 днів. Дикий гусак від північного моря до південного летить 9 днів. Дика качка і дикий гусак вилітають одночасно. Через скільки днів вони зустрінуться?

6. Задача із папірусу Райнда (Єгипет).

Знайти число, коли відомо, що при додаванні до нього його і відніманні від

отриманої суми його третини отримаємо число 10.

7. Задача із «Арифметики» Магніцького.

Один чоловік випиває кадь пиття за 14 днів, а з дружиною вип’є ту ж кадь за 10 днів. За скільки днів вип’є ту ж кадь його дружини самостійно?

8. Задача Брахмагупти (Індія, бл. 598-660рр.).

Слон, слониха та слоненя підійшли до озера, щоб напитися води.

Слон може випити озеро за 3 год., слониха – за 5 год., а слоненя – за 6 год.

За скільки годин вони разом вип’ють озеро?

9. Задача Герона Александрійського (Стародавня Греція, І ст. до н.е.).

Басейн може заповнитися через 4 фонтани.

Якщо відкрити тільки І фонтан, басейн заповниться за добу, тільки ІІ – за 2 доби,

третій – за 3 доби, тільки ІV – за 4 доби.

За який час заповниться басейн, якщо відкрити всі 4 фонтани?

10. Задача з Акмимського папірусу (VI ст.).

Дехто взяв із скарбниці її вмісту. З того, що залишилося, другий взяв .

Після цього у скарбниці залишилося 192 коштовності.

Скільки коштовностей було у скарбниці спочатку?

Тема. Відношення і пропорції.

1. Задача Даламбера.

Яка ймовірність того, що при двох послідовних підкиданнях монети, хоча б

один раз випаде герб?

2. Задача іранського ученого. ХVI ст. Бехаеддіна.

Поділити 10 на дві частини, різниця яких 5.

Тема . Коло. Довжина кола.

1. Древньоіндійська задача Аріабхата (476 - бл. 550)(із трактату «Аріабхатія»)

Додай 4 до 100, помнож на 8 і додай до всього цього 62000. Те, що дістанеш, - наближене значення довжини кола, якщо діаметр 20000. Яку точність числа її забезпечувало застосування цього правила?

= (8* (100 + 4) + 62000): 20000 = 62832:20000 3,1416

Відповідь: 3,1416

Тема: Рівняння.

Древньоєгипетська задача.

Уся купа, її її , її разом становить 37. Скільки в усій купі?

Нехай купа дорівнює х.

Відповідь:16.

Древньоіндійська задача (з Бахшалійського рукопису).

З чотирьох жертвувателів другий дав у двічі більше, ніж перший, третій - втроє більше, ніж другий, четвертий - вчетверо більше, ніж третій, а все разом дали 132. Скільки дав перший?

Нехай перший дав х, тоді другий - 2х, третій - 3*2х, четвертий - 4*3*2х,
тому:

                 х + 2х + 6х + 24х = 132,
                         33х = 132,
                 х = 4

Відповідь: 4

Задача Метродора (ІVст.) (з Палатинської антології).

Прах Діофанта гробниця ховає: вдивися в камінь
Мудрим мистецтвом розкриє покійного вік
З волі богів шосту частину життя був він дитина,
А ще половину шостої — стрів із пушком на щоках.
Тільки минула сьома, з коханою він одружився,
З нею п'ять років проживши, сина діждався мудрець.
Та півжиття свого тішився батько лиш сином:
Рано могила дитину у батька забрала.
Років двічі по два батько оплакував сина.
А по роках цих і сам стрів він кінець свій печальний.
Задача зводиться до рівняння

х=84

Відповідь: 84 роки.

Із папірусу Ахмеса.

Кількість і його четверта частина дають разом 15.

Із Московського папірусу.

Число і його половина складають 9. Знайти число.

Із книги «Косс» Адама Різе.

Троє виграли деяку сумі грошей. На долю першого випало цієї суми, на
долю другого , а на долю третього 17 флоринів. Яка величина виграшу?

7. Задача Ал-Хорезмі (арабські задачі).

Знайти таке число, що коли відняти від нього і його, то в остачі буде 8.

8. Задачі із «Арифметики» Магніцького.

Дехто прийшов, купив іграшки для малих дітей: за І іграшку заплатив частину

всіх своїх грошей, за ІІ – того, що залишилося, за ІІІ іграшку заплатив остачі від

ІІ покупки, а після приїзду додому знайшов решту 1 руб. 92 коп. Скільки грошей

було і скільки за яку іграшку грошей заплачено?

9) Задачі із «Курсу чистої математики» Є.Д.Войтяховського:

а) Капітан на запитання, скільки в його команді людей, відповідав що його

команди в караулі, на роботі, в лазареті і 27 в наявності.

Запитується, скільки людей в його команді?

б) Собака побачила за 150 сажнів зайця, який перебігає за 2 хвилини 500 сажнів,

а собака за 5 хвилин – 1300 сажнів.

Запитується, за який час собака дожене зайця?

в) Веселий француз прийшов у трактир з невідомою сумою свого багатства,

позичив у господаря стільки грошей, скільки мав у себе; із цієї суми витратив

1 рубель. Із залишком прийшов у другий трактир, де знову, позичивши

стільки скільки мав,

витратив в ньому також 1 рубель; потім прийшов в третій і четвертий трактир,

вчинив так само, а коли вийшов з четвертого трактиру, не мав нічого.

Запитується кількість його грошей.

7 клас, алгебра

Тема: Лінійні рівняння з однією змінною.

Задача Метродора (з Палатинської антології, ІVст.)

Уздрівши, що плаче Ерот, Кіпріда його запитала!

«Що тебе так засмутило, хотіла б я знати?»

«Із Гелікона ішов я, ніс яблук чимало,— Ерот на те каже,—

Та музи, раптово напавши, солодку загарбали ношу.

Долю двадцяту вмить захопила Евтерпа, а Кліо

П'яту частину вділила, і Талія — восьму.

Долю двадцяту забрала собі Мельпомена, а чверть — Терпсихора. Сьому частину поцупивши, зникла, мов привид, Ерато. Тридцять плодів узяла Полімнія. Сто двадцять Уранії тут перепало, а триста плодів — Калліопі.

Тож повертаюсь додому я майже з пустими руками. Тільки півсотні лишилося яблук у мене».

Нехай х - кількість блук, які ніс Ерот.

х - х -х - х - х - х -30 – 120 – 300=50,

х = 500,

х = 3360

Відповідь: 3360 яблук.

Задача Ісаака Ньютона, англійського вченого (ХVІІст.)

Два листоноші А і В, між якими 59 миль, виїжджають вранці назустріч один одному. Листоноша А проїжджає за 2 год 7 миль, В — за 3 год 8 миль; при цьому В вирушає в дорогу на годину пізніше, ніж А. Скільки миль проїде А до зустрічі з В?

Відповідь: 35миль.

Задача Ананія Ширакаці (середина VІІст.)

Один купець пройшов через 3 міста. У першому місті у нього взяли половину і третину майна, у другому половину і третину того, що у нього лишилося, у третьому знову половину і третину того, що у нього було.

Коли він прибув додому, у нього лишилося 11 грошів. Скільки всього грошів було спочатку у купця?

Відповідь: 2376 грошів.

4. Задача із «Математики в дев'яти книгах»

Є 9 злитків золота і 11 злитків срібла, їх зважили, і вага співпала. Переклали злиток золота і срібла, золото стало легше на 13 ланів. Питається яка вага злитка золота і злитка срібла, кожного зокрема?

Відповідь: х = 35 лан, y = 29 лан.

5. Задача із Древньої Греції.

На запитання, скільки учнів навчається в школі, Піфагор відповів: «Половина

всіх учнів вивчає математику, чверть – музику, сьома частина мовчить і крім того,

є ще 3 жінки». Скільки учнів у Піфагора?

6. Стародавня індійська задача.

З букету квіток лотоса принесено в жертву: Шіві – третю частину, Вішну – п'яту,

Сонцю – шосту. Одну чверть одержав Бхавані, а решту, 6 лотосів,

дано глибокошанованому вчителеві. Скільки було квіток у букеті?

7. Стародавня китайська задача.

Кілька чоловік разом купують барана. Якщо кожен внесе по 5 монет, то не вистачить

до вартості барана 45. Якщо кожен внесе по 7, то не вистачить 3. Скільки коштує баран?

8. Задача з фольклору США.

Мері 24 роки. Це в 2 рази більше, ніж було Анні, коли Мері було стільки років,

скільки тепер Анні. Скільки років Анні?

9. Задача з турецького фольклору.

Старий Ісхан мав дітей, онуків, правнуків і праправнуків. Всього їх разом з Ісханом

було 2801. Праправнуки були ще маленькі, тож не мали дітей, а всі інші

мали по однаковій кількості дітей, і всі діти були живі і здорові. Скільки дітей

мав старий Ісхан?

10.Задача з болгарського фольклору.

Пастух пасе череду із 100 голів, защо одержує 100 левів. Скільки в череді волів, корів

і телят, якщо за одного вола він одержує 10 левів, за корову – 5 левів, а за теля – 0,5 лева?

Тема: Цілі вирази

1. Задачі Піфагора (Стародавня Греція).

а) Сума будь-якого числа послідовних непарних чисел, починаючи з одиниці,

є точний квадрат.

б) Будь-яке непарне число, крім одиниці, є різницею двох квадратів.

В піфагорійській школі ці твердження доводились на часткових прикладах.

Переконайтесь в правильності тверджень.

2. Із «Начал» Евкліда (ІІ книга).

а) ²²;

б) (2а+в)в+а²=(а+в)²;

в) (а+в)²+а²=2(а+в)а+в²;

г) 4(а+в/а+в²=((а+в)²+а)²;

д) а²+в²=2;

3. Із «Універсальної арифметики» Ейлера.

а) (р²+q²)²=(р²-q²)²+(2рq)²;

б) (р²+q²)⁴=(р⁴+6р²q²+q⁴)+(4р³q-4рq³)².

Тема: Формули скороченого множення.

1. Задача з «Арифметики»Діофанта

(а² +b²)(с² + d²) = (ас + bd)² +(аd + bс)²

Тема: Лінійне рівняння з двома змінними. Системи лінійних рівнянь з двома змінними.

Задача Діофанта з його книги «Арифметики» (Шст.)

Знайти два невід'ємних числа, різниця між якими в 6 раз більша від різниці їх квадратів.

Задача зводиться до рівняння

х-у = 6(х² +у²),або х + у =

Розв'язок буде нескінченне множення пар і т. д.

2.Задача Магавіри, індійського вченого IX ст.. (із книги» Короткий курс математики»).

Під час бою півнів один з глядачів домовився з двома власниками півнів. Першому він сказав: «Якщо переможе твій півень, то виграш віддаси мені, якщо ж програєш, то я сплачу

тобі твого можливого виграшу». Другому учаснику він сказав: «Якщо переможе твій півень, то виграш віддаси мені, якщо ж програєш, я сплачу тобі можливого виграшу». В обох випадках глядач одержить 12 монет. Який мав бути виграш кожного учасника бою?

Позначивши через х і у виграші кожного партнера, дістанемо систему.

Звідси х=42, у=40.

3.Задача китайського математика Сунь - Цзи (Шст. Збірник «Математичний трактат»)

Два чоловіки А і Б одержали деяку кількість монет, які треба розділити між ними так, що коли до монет А додати половину монет Б або до монет Б додати монет А, то в обох випадках дістанемо 48. Скільки монет одержав кожний чоловік?

Якщо позначити кількість монет А через х, а кількість монет Б — через у, то :

Звідси х=36, у=24

4. Древньоіндійська задача XI ст.. («Математика» Сріддхари).

Є кадамба - цвіток,

На одну з пелюсток

Бджілок п'ята частина спустилась.

Поряд з нею росла

Вся в квіту сименгда

І на ній третя частина розмістилась.

Їх різницю знайди,

Її тричі склади

ї тих бджіл на Кутай посади.

Лиш одна не знайшла
Собі місця ніде,

Все літала то взад, то вперед, і завжди

Ароматом квіток любувалась

І назви ти мені, полічивши в умі,

Скільки бджілок всього тут зібралось.

5. Задача Ісаака Ньютона.

Купець мав деяку суму грошей. 100 фунтів із неї він витрачав кожен рік на
утримання своєї сім'ї, додаючи до суми, що залишилася, її третину. Через З
роки він виявив, що його статки подвоїлись. Скільки грошей було у нього
спочатку?

6. Із «Алгебри» арабського математика і астронома ал-Караджі (Х – ХІ ст.).

Розв'язати:

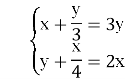
7. Стародавня грецька задача.

Навантажені осел і мул ідуть повільно. Осел скаржиться на важку ношу, мул йому відповідає: «Чому ти скаржишся? Коли б я взяв твій один мішок, то моя б ноша стала в два рази важча від твоєї. А коли б ти взяв мій мішок, то твоя ноша б дорівнювала моїй». То скільки мішків несли осел і мул?

8. Стародавня китайська задача.

5 волів і два барани коштують одинадцять таєлів, а 2 воли і 8 баранів – 8 таєлів.

Скільки баранів можна купити за гроші, одержані від продажу 5 волів?

9. Задача із трактату «Дев'ять відділів мистецтва рахунку» (Древній Китай).

Із трьох бочок рису однакового об’єму вкрадено трьома злодіями деяка кількість рису.

В 1 бочці залишився1 го рису, в другій – 1 шинг 4 го і в третій – 1 го.

Злодії сказали:1-й, що він відсипав рис з першої бочки лопатою; 2-й,

що він користувався дерев'яним черевиком, а 3-й – мискою, причому

вони відповідно брали із другої і третьої бочок. Об'єм лопати – 1 шинг 9 го,

черевика – 1 шинг 7 го, миски – 1 шинг 2 го.10 го – 1 шинг, 10 шинг – 1 тау,

10 тау – 1 шинг.

Скільки вкрав кожен злодій?

Тема: Многочлени і дії над ними.

1. Із «Універсальної Арифметики» Л. Ейлера.

Довести тотожність:

7 клас, геометрія

Тема: Коло і круг. Геометричні побудови.

1. Задача Аполлонія Перського, (бл. 260 - 170 рр. до н.е.) математика епохи еллінізму (книга «Про дотикання»)

Дано три фігури, кожна з яких може бути точкою, прямою або колом. Побудувати коло, яке проходило б через кожну з даних точок і дотикалося б до кожної з даних прямих або кожного з даних кіл.

Обмежимося одним випадком; побудувати коло, яке дотикається до двох даних паралельних прямих і даного кола.

Нехай дано прямі а і в, і коло з центром О і радіусом г.

З довільної точки А (Аа) побудуємо АВа
Знаходимо точку С - Середину прямої АВ, і через неї проводжу ва
Будуємо коло з центром в точці О радіуса (г+АС) або (г-АС).дане коло перетинає пряму в точці D.
Будуємо коло з центром в точці В радіуса АС.

Задача італійського математика Ніколо Тарталья (1500 - 1557р.)

На даному відрізку АВ побудувати за допомогою лінійки і даного розхилу циркуля, який не дорівнює АВ , рівносторонній трикутник

1.Будуємо пряму а ( АВ а)

2.Будуємо коло з центром в точці А даного радіуса, яке перетинає пряму а в точці D.

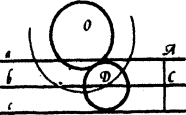
<В

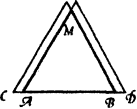
3.Будуємо коло з центром в точці В даного радіуса, яке перетинає пряму а в точці С.

4.Будуємо на AD і ВС рівносторонній трикутники, які перетинаються в точці М

АМС - шуканий.

3. Задача із книги «Начала» Евкліда.

Нехай дано трикутник ВС і точка А поза нею: через точку А Провести пряму,

Паралельну ВС.

Розв'язання (Евкліда)

Візьмемо на ВС довільну точку D і, сполучивши А з D, побудуємо кут DАЕ який дорівнює куту АDС. Оскільки пряма АD, яка падає на ВС, ЕF, утворила кути ЕАD, АDС, що лежать навхрест і рівні між собою, то ЕF паралельна ВС.

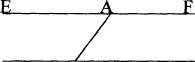
$C:\Users\1\AppData\Local\Temp\FineReader10\media\image1.png$

В D С

8 клас, алгебра

Тема: Раціональні вирази.

1. Задача Дай Шу (Давнокитайська)

Спростити вираз:

Задача була запропонована в 1908 році на випускному екзамені філфаку

(І - Сіо - Гуань) Бейпінського університету.

Задача з «Арифметики» Діофанта

- =

3.Із «Загальної арифметики» Ньютона.

Скоротити дроби:

a) ; б).

4.Із «Арифметики» Діофанта.

а) ;

б) .

5. Виконати дії (із «Арифметики» М.Штіфеля).

а) ;

б) ;

в) ;

г) .

6. Скоротити дроби (із «Загальної арифметики» Ньютона).

а) ;

б)

Тема: Квадратні корені. Дійсні числа.

Задача італійського математика Луки Пачолі (ХVст.) (із книги «Сума
знань з арифметики, геометрії, відношень і пропорцій)

Звести до раціонального вигляду знаменник дробу

===

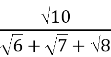
2. Давньоіндійська задача Апастамби (V - IV ст. до н. е.)

Довести рівність:

а)

(з книги «Шульва-сутра»)

б) + - , в) + .

3. Задача Бхаскари ІІ

а)

б)

4. Древньоіндійська задача.

Знайти число, яке, будучи помноженим на 3, потім поділеним на 5, збільшеним на 6, після чого, якщо з нього добувається квадратний корінь, віднімається одиниця і підноситься до квадрату, дає 4. Відповідь: 5

5. Задача Бхаскари.

6. Із Бахшалійського рукопису.

Посеред бою син Прітхи схопив деяку кількість стріл, щоби вбити Карну: половину

їх він використав на власний захист,

а почетверену кількість квадратного кореня –

проти коней; 6 стріл пронизали візника Салью, 3 інших прорвали парасольку

Карни, розбили його лук і прапор, і тільки одна остання пронизала йому голову.

Скільки було стріл у Арджуни (сина Прітхи)?

Тема: Квадратні рівняння

1. Задача Магавіри, індійського вченого IX ст.

Відомо, що череди верблюдів пасеться в лісі, 15 — на березі річки,а решта — подвоєний квадратний корінь із загальної кількості верблюдів — на схилахпагорба.

Скільки верблюдів у череді?

Нехай х - кількість верблюдів у череді, тоді х+ 2

2. Задача Магавіри.

Дев'ять коренів ззагальної кількості слонів, складені з 6 коренями остачі, знаходяться в лісі. Є ще 24 слони. Скільки всіх слонів?

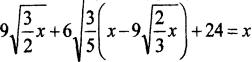
Нехай усього було х слонів.

Розв'язування його Магавіра зводить до послідовного розв'язання двох квадратних рівнянь. Позначивши.

Дістає квадратне рівняння

y-6y=24,

Одержує:

Зробивши заміну, одержує:

Квадратне рівняння

не має цілих коренів.

Відповідь: 150 слонів.

3.Задача індійського математика Бхаскари ІІ (1115 - 11873) (трактат «Лілаваті»)

На дві партії розбившись,

Мавпи бавилися в гаї.

Частка восьма їх в квадраті

Забавлялася, стрибала.

Криком радісним дванадцять

Тихе світло дня вітали.

А тепер скажи, юначе,

Скільки мавп було у гаї?

Нехай у гаї було х мавп, тоді

Звідки = 48, =16

4. Задача перського математика Омара Хайяма (1048 - 1131рр.)

Розв'язати рівняння:

+ 2 = 1

Відповідь: х=2

5. Задача італійського математика Рафаеле Бомбеллі (1526 - 1573рр.)

Розв'язати рівняння:

х³ = 15х+4

х³ - 4х² + 4х² - 16х + х- 4 = 0;
х² (х - 4) + 4х(х - 4) + (х - 4) = 0;
(х-4)(х² +4х+1) = 0
х, =4, х_{2, 3} = 2± 3

6.Задача Леонарда Пізанського (Фібоначчі) (1180 - 1240) («Книга абака»)

Знайти число, якого дорівнює квадрату самого числа.

7. Задача Авіценни.

Знайти число, яке дорівнює добутку його на цього числа.

8. Задача Ейлера.

Знайти число, четвертий степінь якого, поділений на половину самого

числа і збільшений на дорівнює 100.

9. Стародавня китайська задача.

Два чоловіки одночасно вийшли з одного міста: В на схід, а А, пройшовши 10 бу на південь, повернув на північний схід до В. Яку відстань пройшов кожний з них, якщо за годину А проходив 7 бу, а В – тільки 3 бу?

10. Розв'язати рівняння:

а) (Бхаскара);

б) (Декарт).

11. Задача із Бахшалійського рукопису (Індія).

Скільки мавп у зграї, якщо квадрат п'ятої частини, зменшений на 3, сховався в печері і тільки одна залишилась, залізши на дерево?

12. Задачі ал-Хорезмі.

Розв'язати квадратні рівняння:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

13. Задача із «Арифметики» Магніцького.

Знайти число, знаючи, що додавши його квадрат до 108, одержимо число, в 24 рази більше шуканого.

14. Древня індійська задача.

Подесятирений корінь квадратний із стада лебедів полетів у напрямі до озера, помітивши, що збираються хмари. Восьма частина всіх лебедів сховалася в ненюфарах (квітучі водяні рослини), і тільки 6 лебедів безпечно плескались на хвилях. Скажи мені, скільки всіх лебедів?

15. Задача ал-Кархі (арабська).

Знайти число, яке при множенні на дає 1.

8 клас, геометрія

Тема: Многокутники. Чотирикутники. Площі многокутників.
1. Давньовавілонська задача.

Сума площ двох квадратів дорівнює 25 кв. од. Сторона одного

квадрата на 5 лінійних одиниць довша від сторони другого квадрата.

Обчислити довжину сторони кожного квадрата.

Якщо позначити через х і у шукані довжини сторін квадратів, то

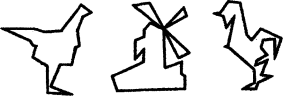
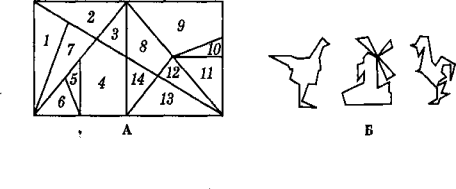
2. Стомахіон Архімеда

        Прямокутник, сторони якого відносяться як 1:2, розрізали на 14 частин
             (додаток 3). Складіть з цих частин силует курки, вітряка, півня.
             Стомахіон (грецьке) — те, що викликає зміст

$C:\Users\1\AppData\Local\Temp\FineReader10\media\image1.png$

3. Задача Абу - Л - Вафа, багдадського математика (940 - 998рр.)

Побудувати квадрат з двох даних неконгруентних квадратів.

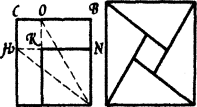
$C:\Users\1\AppData\Local\Temp\FineReader10\media\image2.png$

D P A=M

           Нехай дано два неконгруентних квадрати АВСБD і МNKP і перший більший
          від другого. Накладемо менший квадрат на більший, щоб вершини А і М
          сумістилися.

4. Задача Евкліда (бл. 365 - бл. 300рр. до н. е.) (Начала).

Побудувати паралелограм, рівновеликий даному АВС, за даним гострим
кутом .

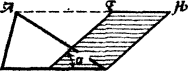
$C:\Users\1\AppData\Local\Temp\FineReader10\media\image3.png$

B D C

Побудуємо ВD=DC, ЕDС=, СН ІI DE і АН II ВС
EDCH - шуканий паралелограм.

5. Задача Евкліда (про золотий поділ).

Даний відрізок АВ точкою Р поділить так, щоб виконувалась умова: АР : РВ = РВ : АВ.

6. Задача Ейлера.

Доведіть, що в кожному чотирикутнику сума квадратів сторін дорівнює сумі квадратів його діагоналей і чотирьох квадратів відрізка, який сполучає середини діагоналей.

7. Єгипетська задача (із Московського папірусу).

Визначити довжини сторін прякутника, якщо відомо їх відношення і площа фігури.

8. Задача Птолемея (Греція).

Довести, що в чотирикутнику, вписаному в коло, сума добутків протилежних сторін дорівнює добутку діагоналей.

9. (З книги Апостолової, ст. 103).

Як із прямокутника вирізати ромб найбільшої площі?

Розв’яжіть кілька задач відомого українського математика М. В. Остро- градського (1801-1862).

У дане коло впишіть трикутник, кожна сторона якого (або їх продовження) проходить через одну із заданих трьох точок.
У дане коло впишіть трикутник, дві сторони якого проходять через задані дві точки, а третя сторона паралельна даній прямій.
У дане коло впишіть чотирикутник, кожна сторона якого (або їх продовження) проходить через одну із заданих чотирьох точок.

У дане коло впишіть трапецію, яка має дану висоту і дану площу.

Тема. Многокутники. Площі многокутників.

1. Задача ал-Хорезмі.

Знайдіть сторону квадрата, вписаного в рівнобедрений трикутник з бічною стороною 10 і основою 12.

2. Задача із папірусу Райнда (Єгипет).

Для обчислення площі рівнобічної трапеції брати добуток півсуми основ на бічну сторону. Обчислити у відсотках похибку, якщо нижня основа 6, верхня 4, бічна сторона 20.

Тема:Подібність трикутників.
1.Древньовавілонська задача.

Прямокутний трикутник АВС поділити лінією DЕ || ВС на трапецію ВСЕD (площиною ) і АDЕ (42 площиною). Обчислити УС = АЕ = у₂, DЕ = х, і
, якщо ВС = 30, - =42, у₂ - = 20

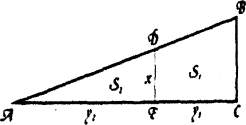
Відповідь: х = 18, = 40, у₂ =60

2.3адача Менелая Александрійського (І - II ст..) (книга Сферика).

Якщо перетинає сторони АВС або їх продовження у точках то справджується відношення

Побудувати СО || АВ, дістанемо дві пари подібних трикутників: ААВіСі - А СОВі іАВАїСі - А САіО. З подібності першої пари випадає:

Побудувати CG AB, дістанемо дві пари подібних трикутників: A - і - . З подібної першої пари випадає:

а з другої пари:

Поділивши (2) на (1), маємо:

Помноживши обидві частини рівності (3 )на , дістанемо:

3. Задача Бхаскари.

Квітка лотоса при вертикальному положенні стебла піднімалася над водою на фута. Вітер відхилив її на 2 фути від попереднього положення (по поверхні води). Після цього квітка лотоса опинилася на рівні води. Визначте глибину озера в цьому місці.

4. Задача Архімеда.

Якщо хорди АВ і CD кола перетинаються в точці Р під прямим кутом, то сума квадратів відрізків АР, ВР, СР і DР дорівнює квадрату діаметра кола. Доведіть.

5. Задача ал-Каші.

Спис стояв у воді вертикально і піднімався над водою на 3 лікті. Вітер відхилив його так, що вершина списа зрівнялася з поверхнею води на відстані 5 ліктів від початкового положення списа. Знайдіть довжину списа.

6. Задача Евкліда.

В дане коло впишіть трикутник, подібний даному трикутнику.

7. (Зкниги Апостолової ст. 116).

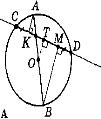Лема Архімеда про перпендикуляри на січну

Коло і перпендикуляри, проведені з кінців діаметра на січну, відтинають на ній рівні відрізки.

Доведення

Можливі два випадки: діаметр і січна перетинаються всередині кола; січна перетинає не діаметр, а його продовження.

ВИПАДОК 1.

Нехай діаметр АВ і січна СD перетинаються всередині кола (мал. А), О - діаметр кола.

Проведемо ОТ ⟘СВ,АK⟘ СD, ВМ⟘ СD.

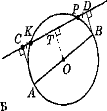Тоді СТ = ТD.

АК ОТ МВ і КТ : ТМ = АО : ОВ.
АО = ОВ як радіуси. Тоді КТ = ТМ (див. с. 80).
СК = СТ-КТ=ТD-ТМ = МD.

ВИПАДОК 2.

У випадку, коли січна перетинає не діаметр, а його продовження (мал. Б), рівність СК = РD доводиться аналогічно. Переконайтеся в цьому самостійно

Тема: Розв'язування прямокутних трикутників.

1. Давньовавілонська задача.

Балка завдовжки 0,5 гар (гар дорівнює 12 ліктів) стояла вертикально в положенні АВ. Потім вона зайняла положення СD . ВС = 0,1 гар. На скільки ліктів віддалився нижній кінець балки від попереднього положення?

У прямокутному = 6 ліктів, AC = 4,8 ліктів. Тоді

AD= 12.96 = 3,66(ліктів)

Стародавні вавілоняни більше ніж за 1600 років до Піфагора знали й використовували для розв'язання задач теорему, названу його ім'ям.

2. Теорема Піфагора Самоського (570 - 496 рр. до н.е.)

Площа квадрата, побудованого на гіпотенузі прямокутного трикутника, рівновелика сумі площ квадратів, побудованих на його катетах. За даними на малюнку довести теорему Піфагора, а саме, що

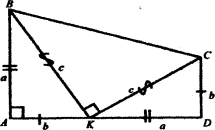$C:\Users\1\AppData\Local\Temp\FineReader10\media\image1.png$ с²=а²+b²

Доведення

На малюнку зображено прямокутну трапецію АВСD з основами СD = b та
АВ = а; DА = а + b - висота трапеції.
За формулою площі трапеції маємо:

(а + b)² ,(4)

З іншого боку, трапеція складається з прямокутних трикутників АВК, ВКС,
СDК. Тому її площа дорівнює сумі площ цих трикутників, тобто

Відомо, що площа прямокутного трикутника дорівнює половині добутку
катетів. Отже:

=ab,

Тоді:

Прирівняємо праві частини рівностей (4) і (5):

Як бачимо, в цій задачі використовують те, що:

-у прямокутній трапеції одна бічна сторона є висотою;

-площа фігури дорівнює сумі площ фігур, з яких вона складається;

- площа прямокутного трикутника дорівнює півдобутку катетів;

- квадрат суми двох виразів дорівнює сумі квадратів цих виразів і подвоєного їх добутку.

3. Задача Бхаскари II (у книжці «Вінок знання»)

Бхаскара II наводить доведення Піфагора у вигляді креслення з підписом «Дивись!». Дістати з креслення Бхаскари II

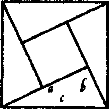доведення теореми Піфагора.

Площа квадрата, побудованого на гіпотенузі с трикутника, рівновелика сумі площ чотирьох прямокутних трикутників і квадрата, довжина сторони якого

(а- b). Тобто,

звідки

4. Задача з древньокитайського «Трактату про мірну віху»

Доведення теореми Піфагора ґрунтується на кресленні, де квадрат побудований

на сумі катетів а і в прямокутного трикутника. Відтворити це доведення.

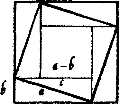
$C:\Users\1\AppData\Local\Temp\FineReader10\media\image3.png$

(а + b)² =4 аb + (а-b)² =2аb + с²
Тому а² + 2 аb + b² = 2аb + с²,

а² +b² =с²

5. Давньоіндійська задача.

Над озером тихим.

Висотою з півфута

Підіймалася лотоса квітка

Яка росла одиноко.

Та вітер скаженим поривом

Відніс її бік .

І не стало видно квітки над водою.

Знайшов її тільки рибалка ранньою весною

В двох футах від місця,

Де вона росла.

І так, пропоную я вам запитання:

Яка в цьому місці на озері води глибина?

Задача Леонардо Пізанського (Фібоначчі) (XII - ХІІІст.)

Дві вежі, одна заввишки 40, а друга ЗО футів, знаходяться на відстані 50 футів одна від одної. До розміщеної між ними криниці злітаються одночасно з обох веж два птахи. Якщо птахи летять з однаковою швидкістю, то вони одночасно долітають до криниці. Знайти відстань від криниці до веж.

Відповідь: 18 футів, 32 фути.

Задача Архімеда ал - Біруні (973 -1048) арабського математика.

Знаючи висоту гори, яка знаходиться на відкритій місцевості, визначити радіус землі.

Нехай висота гори АМ=Н. Вимірявши , дістанемо:

R = (R + Н) , звідки :

R=,

8. Задача Л.М. Толстого

Очеретина звисає над водою на один аршин. Визначити глибину річки, де росте очеретина, не вириваючи її і не вимірюючи глибини ні веслом, ні будь- яким іншим предметом

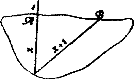
Відхиляємо очеретину так, щоб її верхівка була на поверхні води, і
позначаємо це місце. Вимірюємо АВ. Якщо висота очеретини над водою 1, то

(х + 1)² =х²+АВ²

9) Задача Діофанта.

Знайдіть сторони прямокутного трикутника, якщо вони дорівнюють х³, х³-х,

х³+х, де х – якесь число.

10) Стародавня китайська задача.

Є горизонтальний катет у 5 бу і вертикальний катет у 12 бу. Знайдіть

сторону квадрата, вписаного в цей трикутник.

Тема. Теорема Фалеса. Вписані та центральні кути.

(З книги Апостолової, ст. 18, 36, 40, 61, 82, 87).

1.Всесвітньо відомий український математик Василь Петрович Єрмаков (1845-1922), професор Київського університету, член-кореспондент Петербурзької академії наук, народився в селі Терюха Гомельської області. Він відомий не лише своїми працями з вищої математики, а й задачами, які складав, у тому числі й геометричними. Спробуйте розв’язати одну з них.

Дано два рівні кола, що не мають спільних точок. На їхніх двох внутрішніх дотичних позначили дві довільні точки F і .3 них до кожного кола можна провести ще по одній дотичній. Нехай нові дотичні, проведені з точок F i до першого кола, перетинаються в точці А, а до другого - у точці В. Треба довести, що:

пряма АВ — паралельна прямій, яка сполучає центри кіл;
пряма, яка містить середини FF₁ і АВ, проходить через середину відрізка, що сполучає центри даних кіл.

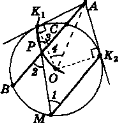
2. Архімед був великим геометром стародавнього світу (див. с. 35). Його трактати «Книга про круги, що дотикаються», «Про кулю і циліндр», «Про тіла обертання»,«Про вимірювання круга» та інші мали велике значення для розвитку математики. Спробуйте (за наведеним малюнком) довести таку лему Архімеда.

Якщо з точки А провести до кола дві дотичні А і А та січну, яка перетинає коло в точках С і В, а з точки К₂ — хорду К₂М || АВ, то пряма М поділить хорду ВС навпіл.

3.Аполлоній Пергськкй (бл. 262 - 190 рр. до н. е.), автор багатьох математичних праць, був молодший за Архімеда років на 25. З його 8 книг про теорію кривих до нас дійшли перші чотири в грецькому оригіналі, п’ята, шоста і сьома - в арабському перекладі, восьма відновлена за розповідями про неї. Саме в останній він розглядав такі задачі на побудову кола:

«Дано три фігури, кожна з яких може бути точкою, прямою або колом. Побудувати коло, яке проходило б через кожну з даних точок і дотикалося б до кожної з даних прямих, кожного з даних кіл».

Розв’яжіть кілька таких задач.

1.Побудуйте коло, яке проходить через три задані точки.

2.Побудуйте коло, яке дотикається до трьох заданих попарно непаралельних прямих. Скільки розв’язків має задача?

3.Побудуйте коло, яке дотикається до двох даних паралельних прямих і проходить через дану точку, що міститься між даними прямими.

4.Побудуйте коло, яке дотикається до двох даних паралельних прямих і даного кола.

5.Побудуйте коло, яке дотикається до двох даних концентричних кіл і проходить через задану точку на одному з цих кіл.

6. Побудуйте коло, яке дотикається до двох даних концентричних кіл і проходить через задану точку, розміщену між цими колами.

4.Арабський математик Гасан Ібн Гайтем (XI ст.) запропонував такий спосіб виявлення того, що заданий чотирикутник є вписаним, при цьому він користувався лише циркулем.

Якщо накреслено чотирикутник АВСD, Гасан Ібн Гайтем пропонує одним і тим самим розхилом циркуля провести дуги з центрами у протилежних вершинах Аі C. Точки перетину дуг зі сторонами чотирикутника та продовженням однієї з них позначимо, як вказано на малюнку. Якщо │ КN│ = │РР│, то чотирикутник АВСD - вписаний, а якщо рівність не виконується - то ні.

Обґрунтуйте спосіб Гасана Ібн Гайтема або спростуйте його.

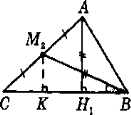5.Розв’язати наступну задачу вам допоможуть теорема Фалеса і малюнок.У трикутнику АВС висота АН₁ дорівнює медіані ВМ₂.

Знайдіть кут СВМ_2.

6.Стомахіон Архімеда. Переказують, що цю гру придумав Архімед.

Прямокутник, сторони якого відносяться як 1: 2, розрізали на 14 частин (мал. А). Складіть із цих частин силует курки, вітряка, півня (мал. Б). Частини прямокутника можна класти на стіл будь-яким боком. Щільне прилягання їх, згідно з вказівкою Архімеда, не обов’язкове. Але при зображенні кожної фігури всі 14 елементів стомахіона мають бути використані.

«Стомахіон» у перекладі з грецької мови означає «те, що викликає злість». Спробуйте свої сили в цій грі, і ви переконаєтесь, що така назва виправдана. Гра повна несподіванок, вона розвиває винахідливість, загострює розум, тренує зір у сприйнятті ліній і форм. Стомахіон - патріарх серед ігор-головоломок. Він витримав 2000-річне випробування і не застарів, як не застаріли теореми і закони Архімеда.

$C:\Users\s\AppData\Local\Temp\FineReader11\media\image2.png$

9 клас, алгебра

Тема. Квадратична функція.

1. Задача Діофанта («Арифметика»).

а) Розв'язати систему:

б) Знайти два числа, сума яких 20, а добуток 96.

в) Знайти три числа, коли відомо, що добуток суми перших двох на третє 35,

суми першого з третім на друге – 27, а суми другого з третім на перше – 32.

2. Задача Кардано (Італія).

Розкласти 10 на два додатки з таким розрахунком, щоб їх добуток дорівнював 40.

Тема: Розв'язування систем рівнянь другого степеня з двома змінними.

Задача з «Арифметики» Діофанта

Знайти два числа, відношення яких дорівнює 3, а відношення суми їх квадратів до їх суми дорівнює 5.

Стародавня задача Єгипетського папірусу (Кахунського папіруса)

Відношення двох чисел дорівнює відношенню 2:1 . Сума їх квадратів

дорівнює 400. Знайти ці числа.

Стародавня англійська задача.

Три селянина Джон, Пітер, Алексіс прийшли на базар із своїми жінками Мері, Кітті і Дженні. Дізнатись, хто з ким одружений, якщо відомо, що кожна з цих шести осіб заплатила за кожну куплену річ стільки пенсів, скільки речей нею куплено. Кожний чоловік витратив на 63 пенси більше, від своєї дружини. Крім того Джон купив на 23 речі більше, ніж Кітті, а Пітер - на 11 речей більше, ніж Мері.

Нехай чоловік купив х речей заплативши за них пенсів. Жінка його купила у речей і заплатила у² пенсів; за умовою

x² - y² = (x + у)(x -у) = 63;

_Причому х і у - цілі числа, отже, можливі три комбінації:

1) 2) 3)

х = 32 х=12 x = 8

y= 31 у = 9 у = 1

Різниця 23 може бути тільки між 32 і 9, отже, 32 речі купив Джон, 9- Кітті,

різниця 11 може бути між 12 і 1, отже, Пітер купив 12 речей, а Мері одну. На

решті, Алексіс купив 8 речей, а Дженні 31. Зрозуміло, що дружиною Джона

була Дженні, Пітера - Кітті і Алексіса - Мері.

Тема: Елементи прикладної математики.

Задача Архімеда

Корона царя Гієрона, виготовлена із золота і срібла, має вагу 10 кг. У воді її вага становить 99,55% її ваги в повітрі. Знаючи, що 1 кг золота втрачає в воді кг, а срібло 9 % своєї ваги в повітрі, обчислити, скільки золота і скільки срібла витратив майстер на виготовлення корони?

Відповідь: Золота—7,1005 кг, срібла—2,8995 кг

Задача Блеза Паскаля (1623 -1662) французького математика

Кавалер де Мере вирішив розбагатіти грою в кості. Він побився об заклад,

що коли кине чотири рази гральну кістку (кубик, на якому вибиті очки від 1 до 6), то; хоча б раз випаде число 6. Якщо ж цього не трапиться (6 не випаде жодного разу з чотирьох кидків) — виграє його супротивник. Для надійності де Мере звернувся до Паскаля, щоб той обчислив імовірність виграшу. Що показали обчислення?

При одному киданні ймовірність випадання 6 очок дорівнює , а ймовірність невипадання . Ймовірність того, що при чотирьох киданнях жодного разу не випаде 6 очок, дорівнює , Отже, ймовірність виграшу для де Мере дорівнювала 1-. При багатократному киданні де Мере майже напевне виграв би.

3.Задача Франсуа Бетрана (1822 - 1900), французького математика

Якось у Неаполі преподобний Галіані побачив чоловіка з Базілікати, який, підкидаючи три гральні кості в кружці, бився об заклад, що викине три шестірки; і справді, він негайно дістав три шестірки. Чоловіку з Базілікати це вдалося вдруге, потім третій, четвертий і п'ятий раз. «Кров вакха! — вигукнув преподобний.

Кості налиті свинцем!?». Чому преподобний запідозрив людину із Базілікати в шахрайстві?

Ймовірність випадання шестірки при одному киданні однієї гральної кості

дорівнює , трьох шестірок при одночасному киданні трьох гральних костей

Ймовірності повторення такої ситуації при наступних киданнях

будуть: при 2-му киданні 3-му ,

4-му і 5-му .

Події (викидання трьох шестірок) швидко ставали все більше неймовірними

4. Давньокитайська задача Суань - Шу.

Є два сорти чаю. 3 фрукти першого змішані з 6 фруктами другого, після чого виявилось,що фрукт суміші коштує 3 дяо ( 30 коп.) Після цього змішали ще 12 фруктів першого сорту з 4 фруктами другого, причому виявилося, що

фрукт суміші коштує 3дяо.

Скільки коштує фрукт першого і другого сор

5. Задача з австралійського фольклору.

Батько пропонував своїм синам Альфреду, Джону і Чарльзу отару своїх овець розподілити так: Альфред одержить на 20% більше від Джона і на 25% більше від Чарльза. Джон одержить 3600 овець. Скільки овець одержить Чарльз?

6. Задача з фольклору Франції.

Заплативши за вечерю в ресторані, Метив'є виявив, що в нього залишилася п'ята частина грошей, які були з собою. Причому сантилів залишилося стільки, скільки спочатку було франків (1 франк = 100 сантилів), а франків залишилось у 5 разів менше, ніж спочатку було сантилів. Скільки заплатив Метив'є за вечерю?

Тема: Числові послідовності.

Древньоєгипетська задача.

Поділити 10 мірок ячменю між 10 людьми так, щоб другий одержав на

мірки ячменю більше, ніж перший, третій – на мірки більше, ніж другий,

..., 10-й - на мірки більше, ніж дев'ятий.

Задача зводиться до обчислення першого члена арифметичної прогресії, різниця якої , а сума десяти членів дорівнює 10.

* ^

Древня китайська задача із « Математики в дев'яти книгах » (II ст.. до н. е.)

Рисак і шкапа рухаються від Чананя до Князівства Ці, відстань між якими

3000 мір довжини. У першй день рисак пробіг 193 міри, а кожного наступного

дня на 13 більше. Шкапа пробігла вперший день 97 мір, а кожного

наступного дня менше. Рисак першим досягнув князівства Ці, повернув назад

і в деякому місці зустрів шкапу.

Через скільки днів вони зустрілися і скільки пробіг до цієї зустрічі кожний?

Рисак і шкапа зустрінуться через 15 дня, рисак пробіжить до зустрічі

4534міри, шкапа 1465міри.

3.Древньоєгипетська задача.

У семи людей по сім кішок; кожна кішка з'їдає по сім мишей, кожна миша з'їдає по сім колосків, із кожного колоска може вирости по сім мірок ячменю. Як завеликі числа цього ряду та їхня сума?

Задача зводиться до обчислення членів і суми членів геометричної прогресії:

7² + 7³ + + = 21407

4. Древньоєгипетська задача із папірусу Райнда

Поділити 10 мірок ячменю між 10 людьми так, щоб другий одержав на

мірки ячменю більше, ніж перший, третій - на - мірки більше, ніж другий,

.. .,10-й - на - мірки більше, ніж дев'ятий.

Задача зводиться до обчислення першого члена арифметичної

прогресії, різниця якої - , а сума десяти членів дорівнює 10. Кожний з

людей одержить:

5.Древньовавілонська задача

Поділити 26"15'45 мір срібла між п'ятьма братами так, щоб кожний одержав на більше за ту кількість срібла, яку одержав наступний за віком брат

Перший брат одержить 7"48'45; другий — 6" 15; третій — 5, четвертий — 4;
п'ятий — 3" 12 міри срібла.

(Примітка: У Вавилоні користувалися шістдесятковою системою числення)

7"48'45 = 7 * 60° + 48 * + 45 * 6
6. Задача французького математика Ніколя Орема (1323 — 1382рр.)

Довести, що:

Сума утворених з членів двох нескінченних спадних геометричних прогресій.

7. Задача Ніколя Орема із трактату «Про конфігурацію якостей» (бл. 1350р.)

Обчислити площу фігури, утвореної з нескінченної множини прямокутників, якщо довжина горизонтальних сторін прямокутників зменшуються у відношенні 4:1, а довжина вертикальних - збільшується у відношенні 1:2.

48	1212	п
		п

Задача зводиться до обчислення суми членів нескінченної спадної геометричної прогресії: 48+24+12+6+...

8. Задача французького математика П’єра Ферма (1601 - 1665рр.)

Якщо 8 - сума нескінченної спадної геометричної прогресії (а_п), то

S:.,

Відомо , що _тоді S-

S-

Поділивши почленно (1) на (2), дістанемо

9. Задача Феофана Прокоповича.

Якась людина має багато коней, і всім їм різна ціна. Найгірший кінь коштує 4

золотих, а найкращий 55 золотих, і ціна від одного до другого коня весь час

піднімається на 3 золотих.

Питаємо: скільки ж усього було коней?

10. Задача Архімеда.

Знайти суму:

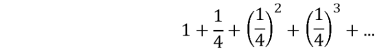
11. Давньогрецька задача.

Доведіть, що в арифметичній прогресії з парним числом членів сума членів

однієї половини більша від суми решти членів на число, кратне квадрату половини

числа членів.

9 клас, геометрія

Тема: Розв'язування трикутників.

1. Задача Луки Пачолі.

Площа трикутника дорівнює 8 кв. од. Обчислити довжини його сторін, коли відомо, що вони виражаються послідовними натуральними числами.

Нехай довжина сторін трикутника х-1, х, х+1, тоді периметр його 3х. За формулою Герона.

84=

Розв'язавши рівняння маємо:

х=14.

Отже, довжина сторін трикутника 13,14,15 (од).

2. Задача Мухамеда ал - Хорезмі.

У трикутної ділянки землі дві сторони по десять ліктів, а третя 12 ліктів, всередині трикутної ділянки квадратна ділянка землі. Обчислити сторони квадрата.

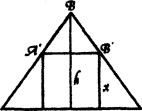
A M D N C

(6-

Позначимо A’B’=x, тоді

(6-x)*x=4x-

тому

48=3x- +3x- -4x-

10x=48,

x=4,8

3. Теорема Піфагора

Площа квадрата, побудованого гіпотенузі прямокутного трикутника, рівновелика площ квадратів, побудованих на його катеті.
Дано АВС СА=b, СВ=а, АВ=с/
Довести: с² = а² +b²,

Доведення

Впишемо в трикутник АВС ( ∟С=90°), коло з центром у точці О.

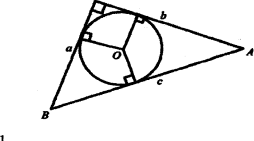
Відомо, що

З іншого боку

Де р = (а+b + с) - Півпериметр трикутника АВС,

г = (а+ b-с) - Радіус вписаного в прямокутний трикутник кола.

З двох рівностей для площі трикутника АВС маємо:

= (а + b + с) = (а + b-с),

аb =((а + b)²-с²),

2аb = а² +2ab + b² -с²,

с²=а²+b²,

Що й потрібно було довести.

4.Древньогрецька задача із трактату «Початки мистецтва обчислення».

Визначити сторони прямокутного трикутника, якщо відомі його площа і
периметр.

5. Задача із папірусу Райнда (Єгипет).

При обчисленні площі рівнобедреного трикутника брати половину

трикутника основи на бічну сторону. Обчислити у відсотках похибку,

якщо основа 4, бічна сторона 10.

Тема: Правильні многокутники.

Задача древньогрецького вченого Архімеда (бл. 287 - 212 рр. до н. е)

Площа круга, описаного навколо квадрата, вдвічі більша за площу круга, вписаного в квадрат.

Задача Архімеда.

Площа круга дорівнює площі прямокутного трикутника, один з катетів якого дорівнює довжині кола, а другий — радіусу цього кола.

3.3адача Дідони. Дідона (пом. бл. 890р.до н. е.).

Дочка арійського царя, втративши чоловіка, убитого її братом, втекла від батька, взявши скриньку з коштовностями. На північному узбережжі Африки король Намідій Ярб погодився продати їй ділянку землі на березі моря «не більше, ніж можна обмежити воловою шкірою». Коли угода відбулась Дідона розрізала шкіру на тонкі смужки і, дякуючи цій хитрості, охватила кусок землі,достатній для побудови фортеці. Так виник Карфаген.

Визначити приблизну площу фортеці, якщо розмір шкіри 4 а ширина ремінців 1мм.довжина ременя (якщо шкіру розрізати по спіралі) 4км. Якщо обмежувати ділянку кривою лінією, то розв'язком буде півкруг з центром на березі моря.

У випадку прямокутної території це квадрат.

4. Задача Гіппократа Хіоського (Уст. До н. е.). давньогрецького математика.

Сума площ серпків (Гіппократа), що лежать між дугою півкола, побудованого на гіпотенузі як на діаметрі, і дугами кругів, побудованих на катетах того самого прямокутного трикутника, рівновелика площі розглядуваного прямокутного трикутника.

Довести, що коли на гіпотенузі і на катетах прямокутного трикутника ж на діаметрах побутувати півкола, то сума площ отриманих серпків дорівнює площі трикутника.

Доведення

Будуємо на гіпотенузі і на катетах прямокутного трикутника АВС як на діаметрах півкола

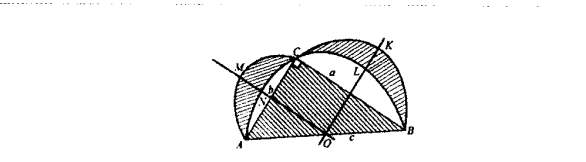
$C:\Users\s\AppData\Local\Temp\FineReader11\media\image1.png$

Вводимо позначення АВ = с, АС = b, ВС=а.

За теоремою Піфагора маємо: а² +b² = с²

Домножимо обидві частини виразу на

тобто сума площ півкругів, побудованих на катетах, дорівнює площі півкруга, побудованого на гіпотенузі.

Віднімемо від кожної частини рівності суму площ сегментів АNС і СLВ.

–,

+=-

Віднявши від площ двох півкругів, побудованих на катетах, площі двох сегментів АNС і СLВ, отримаємо два серпки АМСN і СКВL. Віднявши площі цих самих сегментів від площі півкруга побудованого на гіпотенузі, отримаємо площу трикутника АВС.

Отже, сума площ двох серпків дорівнює площі трикутника:

Що і потрібно було довести.

Не скандальна слава Герострата,

Серце й розум знов беруть в полон.

Загадковий серпик Гіппократа,

Архімеда дивний арбелон.

5. Із папірусу Райнда (Єгипет).

Єгиптяни, заміняючи площу круга площею рівновеликого квадрата,

брали за сторону останнього 8/9 діаметра круга.

Знайти наближене значення для π.

Тема: Декартові координати на площині.

1. Теорема Піфагора

Довести теорему Піфагора методом координат.

Доведення

        Нехай дано трикутник АВС (С=90°), Доведемо, що АВ² = АС² + ВС².
        Виберемо систему координат так, щоб вершина С збігалася з початком відліку,
        а катети лежали на осях.

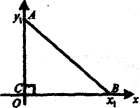
Тоді точка С матиме координати (0; 0), точка В — ( 0), точка А — (0; ).
Знайдемо квадрати відстаней між точками А, В, і С:

АВ² = (, -0)² +(0-)² = +
АС² = (0 - 0)² + (0 - )² =
ВС² =(0-)²+(0-0)² =

Звідки

АВ² = АС² + ВС², що і потрібно було довести.

Тема: Вектори
1. Теорема Піфагора.

Довести теорему Піфагора векторним методом.

Доведення

Нехай дано трикутник АВС (С=90°). Доведемо, що АВ² = СВ² + АС². На

сторонах трикутника побудуємо вектори

Тоді, =+

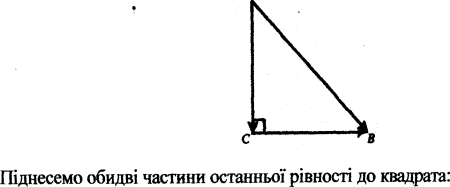
За умовою, тому СВ*ЛС = 0, звідки СВ² + АС² = АВ²,

що й потрібно було довести.

Тема: Початкові відомості з стереометрії.

1. Задача Льва Миколайовича Толстого.

На протилежних стінках кімнати певної довжини й ширини сидять муха і павук. Муха знаходиться на півтора аршина від підлоги, павук на півтора аршина від стелі. Знайти найкоротшу відстань між павуком і мухою.

Нехай довжина кімнати 7 аршинів, ширина — 6, висота — 4. Припустимо, що муха сидить на більшій стіні на відстані 2 аршини, а павук на протилежній стіні на відстані одного аршина від найближчого кута. Виконаємо розгортку кімнати і сполучимо точку, де сидить павук, з точкою, де сидить муха. Можливі три розв'язки (за кількістю різних розгорток). Справді, павук може добиратися до мухи тільки по стінах; по стінах і стелі; по стінах і підлозі. Оскільки відстані від мухи до підлоги і від павука до стелі однакові, то шляхи через підлогу і через стелю мають однакову довжину. За теоремою Піфагора дістанемо: ,

МП_І = 497 14,04;

МП₂ = 10,77;

МП₃ = І45 12,04;

Отже, з трьох можливих розв'язків, найменшим буде 10,77 аршин.

2.Давньоєгипетська задача із Московського папірусу.

Визначити об'єм квадратної зрізаної піраміди, якщо її висота дорівнює 6 ліктів, сторони нижньої основи — 4, верхньої — 2 лікті.

3.Давньоєгипетська задача із папірусу Райнда (або Ахмеса).

Розкласти об'єм 120 кубічних літрів на 10 частин висотою кожна 1 лікоть з

прямокутною основою, сторони якого відносяться як 1:

4.Загадки жерців бога Ра.

Ти стоїш перед стіною, за нею криниця Лотоса, як круг Сонця. Біля криниці покладено один камінь, одне долото, дві очеретини. Довжина однієї очеретини три міри, другої — дві міри. Очеретини перехрещуються на поверхні води криниці Лотоса, а ця поверхня на одну міру вища від дна. Хто повідомить число найдовшої прямої, яка міститься в ободі криниці Лотоса, той візьме обидві очеретини і буде жерцем бога Ра.

Криниця — це прямий циліндр. Дві очеретини приставлені до основи циліндра так, що сума довжин їхніх проекцій на основу циліндра дорівнює діаметру основи циліндра. Обчислити діаметр криниці.

1 спосіб. Нехай АD = х, ВС = у. Тоді х² + АВ² = 9, у² + АВ² = 4,

звідки х² - у² =5

Оскільки AВDВЕF

Оскільки АЕDВЕС,

То х:у = АF:BF тому ху = х + у

Одержимо систему:

Яка приводить до рівняння четвертого степеня.

Добором одержимо.

АВ = 1,231м.

2.спосіб. Стародавні єгиптяни не знали ні теореми Піфагора, ні алгоритму розв'язування систем квадратних рівнянь і рівнянь четвертого степеня. Тому задачу жерців бога Ра вони могли розв'язувати так. На підлозі кімнати креслили крейдою пряму ОР. Враховуючи, що ВD - АС = 1 м, проводили на відстані 1 м. від ОР пряму NМОР. Потім опускали очеретини в криницю і позначали на них місце їх схрещення. Після цього очеретини клали на креслення так, щоб точка схрещення Е лежала на прямій NM, і обертали їх, щоб мокрі кінці очеретин А і В потрапили на першу пряму ОР. Після цього вимірювали наближено АВ.

У 1912 році під час розкопок у дельті Ніла вчені виявили залишки храму, на стінах якого збереглися письмена. Були тут і математичні задачі. Текст цієї задачі жерці бога Ра вирізьбили на стіні велетенської кімнати, побудованої з гранітних брил. Задача була одним з випробувань для бажаючих стати жерцями бога Ра. Це був важкий і небезпечний іспит, про що відверто застерігали жерці. Під її текстом вирізьблено попередження: «Знай: кожний може стати перед стіною. Хто розуміє справу рук жерців бога Ра, тому відкривається стіна для виходу. Але знай: коли ти ввійдеш, ти будеш замурованим. Вийдеш з очеретинами жерцем бога Ра; якщо ж голод переможе твоє тіло, не вийдеш жерцем бога Ра...

Крізь стіну криниці Лотоса пройшло багато, але мало хто став жерцем бога Ра. Думай. Цінуй своє життя. Так радять тобі жерці бога Ра».

Задача справді складна. Можна тільки дивуватися, як з нею справлялися стародавні єгиптяни. Очевидно, не одному з них вона коштувала життя.

Працюючи над задачами далеких епох, не варто ідеалізувати чи надто суворо критикувати минуле. Об'єктивно досліджуючи спадщину минулого, діти бачать, як з неї виростає сучасне. З ранніх математичних текстів доцільно брати найактуальніші задачі. В епоху античної Греції, а тим більше в епоху Відродження і за нового часу математика надзвичайно ускладнилася. Тому звертатися до наукових трактів цих періодів недоцільно, а використовувати на уроках задачі, пов'язані з іменами видатних математиків. Це і задачі тренувального характеру,і нестандартні задачі, пошук розв'язку яких є важливою складовою доступної дітям математичної творчості.

Розв'язання будь - якої достатньо складної задачі вимагає від учня напруженої праці, яка найбільше проявляється тоді, коли діти зацікавлені задачею. Цікаву задачу легше розв'язувати, оскільки вона мобілізує розумову енергію. Тому вчитель повинен підбирати такі задачі, щоб учні хотіли їх розв'язувати, а саме такими є історичні задачі.

АВ = 1,231м.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Нікітюк Марія Михайлівна

Пов’язані теми

Математика, 9 клас, Матеріали до уроків

Додано

15 січня 2023

Переглядів

4504

Оцінка розробки

Відгуки відсутні