"Математика у житті людини: від найдавніших часів до сучасних…"
Математика у житті людини: від найдавніших часів до сучасних…
ЗМІСТ
- Вступ ……………………………………………………………………………..3
- Математика у найдавніші часи …………………………………………………4
- Математика і література…………………………………………………………7
- Математика і судноплавство…………………………………………………….8
- Математика у топографії………………………………………………………..10
- Математика в авіації та космонавтиці…………………………………………14
- Висновки…………………………………………………………………………16
- Список наукової літератури…………………………………………………….17
- Додатки…………………………………………………………………………...18
ВСТУП
Якщо доручити двом людям, один з яких – математик,
виконання будь-якої незнайомої роботи,
то результат завжди буде наступним:
математик зробить її краще.
Штейнгауз Г.
Варто лише показати, що якась річ неможлива,
як знайдеться математик, який її зробить.
Сойєр У.
Перші математичні уявлення і поняття людина формувала в глибокій давнині, розв’язуючи найпростіші задачі практичного характеру. Ускладнювалися форми трудової діяльності, і перед людиною поставали складніші задачі, для розв’язання яких вона формувала нові математичні поняття, створювала математичні теорії.
У сучасному світі людина розуміє, що математичні знання – це необхідність, яку диктує нам наукова революція сьогодення. Застосування математичної теорії на практиці – це те, чому нас вчать сьогодні в школі, з чим ми стикаємось на кожному кроці у нашому житті. Поєднання минулого і сучасного – це наша історія, яку ми створили і створюємо зараз, математика – це теж історія, історія розвитку прогресу, науки. Як майбутні фахівці у різних галузях науки та виробництва, ми повинні знати, розуміти і застосовувати математичні знання у своїй діяльності.
Математика у найдавніші часи
Математика – одна з найдавніших наук. Східна математика виникла як прикладна наука, основною задачею якої були розрахунки, розподіл врожаю, збирання податків. Спочатку були тільки арифметичні розрахунки та виміри. Згодом арифметика перейшла в алгебру, а вже алгебра – в теоретичну геометрію. Прикладом цього є знайдені рукописи Єгипту. На жаль до нас дійшли лише праці Єгипту (відомо, що китайські рукописи були знищені). Один з відомих документів – це єгипетський папірус Райнда (1650 р. до н.е.), так званий єгипетський задачник, який містить умови та розв’язки 84 задач з арифметики та геометрії (в порівнянні з Московським математичним папірусом, який містить лише 25 задач).(додаток 1) Цей рукопис доводить, що всі задачі в єгипетській математиці мали практичний характер. Це були задачі на знаходження площ земельних ділянок трикутної, прямокутної, квадратної форми, площ кругів. Слід згадати той факт, що в Єгипті при будівництві та при вимірі земельних ділянок були присутні так звані землеміри-геометри «гарпедонапти» або «ті, що натягують мотузку», які використовували мотузку з вузлами для побудови прямого кута (3+4+5=12 вузлів). Нам такий трикутник відомий під назвою «єгипетський».(додаток 2)
Також використовувались арифметичні дії, степені, знаходження квадратних коренів, розв’язування рівнянь тощо. Єгиптяни використовували дроби, але на жаль, вони використовували лише аліквотні дроби (тобто дроби виду 1/n). Для того, щоб записати дріб виду m/n вони брали дріб 1/n і множили його на m, що частіше призводило до труднощів при розв’язуванні.
Єгиптяни вміли розв’язувати тільки прості лінійні рівняння, а вавилоняни часів Хаммурапі повністю володіли технікою розв’язування квадратних рівнянь. Від розв’язування лінійних та квадратних рівнянь вони перейшли до рівнянь кубічних та біквадратних. Техніка розв’язування цих рівнянь звичайно відрізняється від сучасної. Широко використовувались також пропорції, відсотки, середнє арифметичне.(додаток 3)
І все-таки насичена теоретична база вавилонської математики не мали цілісного характеру, не було бази з доведеннями тих чи інших фактів. Систематичний підхід в математиці з’явився тільки у греків. Вершиною планіметрії була теорема Піфагора, багато вчених вважають, що вавилонянам вона була відома ще до того як Піфагор її сформулював. Вавилоняни відкрили її між 2000 і 1786 р. до н. е.
У прямокутному трикутнику площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів, побудованих на катетах (формулювання теореми самим Піфагором).
Історію теореми можна розділити на чотири частини: знання про Піфагорові числа, знання про відношення сторін в прямокутному трикутнику, знання про відношення суміжних кутів та доведення теореми. Існує близько 100 різних доведень теореми Піфагора.
Окремо зупинимось на так званих піфагорових числах (трійках). Піфагорові трійки — це три натуральні числа a, b, та c такі, що виконується рівність a2 + b2 = c2. Іншими словами, Піфагорові трійки — це сторони прямокутного трикутника, якщо всі вони є цілочисельними. На мегалітичних спорудах в північній Європі є свідчення, що відомості про такі трійки були відомі до винайдення писемності. Такі трійки зазвичай записують у вигляді (a, b, c). Деякі найвідоміші приклади: (3, 4, 5) та (5, 12, 13).
Примітивними Піфагоровими числами називають такі a, b та c, які є взаємно простими (найбільший спільний дільник a, b та c дорівнює 1)
Нижче наведено перелік примітивних Піфагорових чисел менших за 100:
(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97).
Слід згадати і послідовників Піфагора, його учнів – піфагорійців. Імена піфагорійців мало знані, але вони перші почали науково опрацьовувати царину, якою до них рахівники і геометри займалися практично. Вони зробили з геометрії науку. Перш за все вони ставили перед собою такі завдання, при розв’язанні яких виникли такі терміни як «парабола», «еліпс», «гіпербола». Числа трактували в поєднанні із просторовими величинами, власне при використанні чисел у геометрії зауважили ірраціональні числа.
Найважливішою властивістю чисел піфагорійці вважали парність і непарність і першими ввели поняття парного і непарного числа, простого і складеного, розробили теорію подільності на два.
Одиницю позначали як те, з чого складено числа, і не визнавали числом. Інші числа позначали: 2 – лінія, 3 – пласка геометрична фігура, 4 – геометричне тіло, 5 – властивості фізичних тіл, зокрема барву, 6 – життя, 7 – дух, 8 – любов, 9 – розважливість, справедливість, 10 – досконалість всесвіту.
Вважали унікальними такі числа, у яких сума власних дільників дорівнює самому числу. Наприклад, 6 = 1+2+3. Такі числа називали досконалими. Усі відкриті досконалі числа парні. Також поважали так звані «співдружні» числа: пари чисел, кожне з яких дорівнює сумі дільників іншого. Співдружніми є числа 220 і 284. Піфагорійці знали тільки цю пару і вважали її символом дружби.
Талісманом піфагорійців був правильний п’ятикутник (пентаграма) або інакше піфагорійська зірка, він же був їхнім паролем.
Математика і література
Від часів древніх перейдемо до днів сучасних. Зупинимось на застосуванні знань з математики … у літературі. Згадаємо відомого англійського письменника, автора «Аліси у країні Чудес» Л.Керрола. (додаток 4) Королева Англії, прочитавши книгу про Алісу, попросила інші твори цього письменника і була здивована побачивши конспекти з математичними задачами. Виявляється, автор дитячої книжки був викладачем математики в університеті. Одна з його задач: «У вас є два келихи. Один з них містить 50 столових ложок молока, інший 50 столових ложок води. Візьміть одну столову ложку молока і змішайте його з водою. Тепер візьміть одну столову ложку води і змішайте її з чистим молоком для отримання суміші молоко / вода. Чого більше води в суміші молоко / вода або молока у в суміші вода / молоко?» Логіка і математика – речі, які доповнюють одна одну, і дуже добре, що цей зв'язок ми бачимо у літературі.
Відкриємо книжку А.К.Дойля «Пригоди Шерлока Холмса», з перших сторінок нас захоплюють дедуктивні методи, які використовує англійський детектив Шерлок Холмс. Але і тут ми можемо побачити зв'язок з математикою. Наприклад, оповідання «Обряд роду Масгрейвів». Для того, щоб знайти скарб Шерлок Холмс застосував знання з геометрії про подібність прямокутних трикутників: «Розрахунки були неважкі. Якщо палиця довжиною 6 футів мала тінь довжиною 9 футів, то дерево висотою 64 фути мало б дати тінь довжиною 96 футів». Зауважимо, що висоту в’яза було знайдено одним з героїв оповідання ще раніше: «Мій домашній вчитель вважав, що вивчення тригонометрії можна застосовувати виключно для виміру висот. Я з дитинства знаю висоту всіх дерев і будівель на території маєтку» (додаток 5)
А ось ще одна задача знаменитого детектива: у Шерлока Холмса була, як ви знаєте, справа з танцюючими чоловічками. Він її блискуче розплутав, розгадавши, що криється за таємничими значками, застосувавши просту математичну логіку. (додаток 6)
Математика і судноплавство
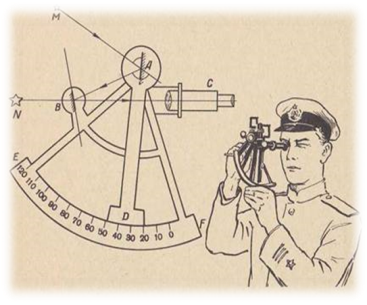
Математика і судноплавство… Перша згадка про морські карти відноситься до 490 р. до н.е. Вони були дуже примітивними і скоріше нагадували креслення. Потреба мореплавців у плаваннях далеко від берегів поставили питання про подальше вдосконалення морських карт, морехідних приладів, поставили на перший план проблему астрономічних спостережень. Тому важливим кроком став винахід інструмента для визначення висоти світил – астролябії (Х ст.). Астролябія – кутомірний інструмент для виміру висот світил, а також горизонтальних кутів при землемірних роботах. В ХV ст. була винайдена лінійка Герсона – кутомірний прилад, який був більш точним, ніж астролябія. Також використовувався такі прилади як сектан (секстант) – інструмент, який призначений для виміру висот небесних світил над видимим горизонтом, а також вертикальних та горизонтальних кутів між орієнтирами вручну, квадрант – інструмент для вимірювання для вимірювання висоти зірок та визначення широти. (додаток 7) Згодом почалася епоха великих географічних відкриттів. Великі морські плавання значно збагатили науку і вплинули на подальший розвиток астрономії, навігації, топографії – основних складових науки про судноводіння.
Навігація вирішує питання визначення напрямів і пройденої відстані в морі; методи обчислення шляху і способи визначення місця судна в морі по береговим і плаваючим орієнтирам за допомогою штурманських приладів; питання керування і безаварійної переводки судна при особливих умовах плавання. У сучасному підручнику «Основи судноводіння» говориться: «Навігація – точна наука, основою якої є математика… Тільки знання наукових математичних основ навігації в поєднанні з досвідом можуть гарантувати безпеку судна в будь-яких умовах плавання».
Картографія допомагає за допомогою теорії картографічних проекцій, що застосовується в судноводінні, розв’язати аналітичним та графічними способами специфічні штурманські задачі про проведенню судна з врахуванням дії різних факторів (вітру, течії та інше).
Всі ці науки побудовані на строгій математичній основі. Але конкретні обставини на морі, інколи дуже складні, не завжди дозволяють штурману отримувати необхідну інформацію з потрібною точністю навіть за допомогою сучасних технічних засобів. Тому судноводіння, яке побудоване на науково-математичній основі, забезпечує безпеку судна при плаванні в будь-яких умовах.
Математика у топографії
Перед тим як буде спроектовано майбутні дороги, газо-і нафтопроводи, лінії електропередач, заводи і житлові будинки, міста і селища, по місцям майбутніх будов мають пройти топографи, геодезисти, геологи. Часто у роботі цих людей виникає необхідність швидко та точно визначити відстань до орієнтирів (цілей) – землемірні роботи, інженерна справа, дії військового характеру та багато іншого. Точні способи вимірювання відстаней за допомогою кутомірних приладів і віддалемірів використовуються при топогеодезичній прив’язці, але ці способи вимірювань потребують багато часу.
Відстані на місцевості залежно від обставин вимірюють такими способами:
а) окомірно;
б) кроками;
в) за спідометром;
г) за кутовими розмірами предметів;
д) за лінійними розмірами предметів;
е) за часом та швидкістю руху;
є) за співвідношенням швидкості світла й звуку;
ж) на слух;
з) побудовою геометричних фігур на місцевості.
Розглянемо деякі з цих способів.
Окомірно - найпростіший та найшвидший спосіб, точність якого залежить від досвіду спостерігача, умов спостереження та величини відстані, що визначається. У досвідченого спостерігача відстань до 1 км може бути визначена з помилкою 10‑15%, у недосвідченого - 30-50%. При збільшенні відстані помилка збільшується. Точність визначення відстані підвищується в результаті систематичних тренувань. При цьому необхідно пам’ятати, що великі та чіткі предмети здаються завжди ближчими; при спостереженні вгору здається, що предмети ближче, а вниз - далі; якщо між спостерігачем і предметом немає інших об’єктів, здається, що він ближче, якщо є - далі; при спостереженні через водні простори, долини та лощини відстані здаються меншими; при спостереженні в сутінках, у тумані, при похмурій погоді відстані здаються більшими.
|
Ознаки видимості |
Відстань |
|
Видно будинки сільського типу |
5 км |
|
Розрізняються вікна в будинках |
4км |
|
Видно окремі будинки, димарі на покрівлі будинків |
3 км |
|
Видно окремих людей |
2 км |
|
Розрізняються стовбури дерев у лісі |
1000 м |
|
Помітні рухи рук та ніг людини |
700 м |
Вимірювання відстані кроками. Рахунок ведеться парами кроків. Після кожної сотні рахунок починається спочатку, а кількість сотен відмічається на папері або іншими способами. Щоб результати були достатньо точними (2‑4% вимірюваної відстані), необхідно тренуватися в ходінні рівними кроками в будь-яких умовах та визначити довжину свого кроку. Для цього потрібно пройти відрізок у 200 м в один бік і навпаки, рахуючи пари кроків, потім 200 м розділити на отриманий середній результат.
Наприклад, при вимірюванні відстані отримаємо 120 та 124 пари кроків. Середнє число пар кроків 122. Довжина пари кроків буде: 200 м : 122 = 1,6 м.
Для приблизного вимірювання довжини кроків можна скористатися формулою:
![]() см, де Д - довжина кроку, см; P - зріст людини, см.
см, де Д - довжина кроку, см; P - зріст людини, см.
Визначення відстаней за лінійними розмірами предметів полягає в наступному. Лінійкою, розташованою на відстані 50 см від очей, вимірюють у міліметрах висоту предмета, що спостерігається. Потім висоту предмета в сантиметрахділять на виміряну лінійкою в міліметрах, результат множать на постійне число 5; отримують відстань до предмета в метрах.
Наприклад, телеграфний стовп висотою 6 м затуляє на лінійці відрізок 10 мм. Отже відстань до нього:
![]()
Точність визначення відстаней за кутовими та лінійними величинами складає 10-15% довжини виміряної відстані. (додаток 8)
Визначення відстані геометричною побудовою на місцевості. Цей спосіб може застосовуватися при визначенні ширини важкопрохідних або непрохідних ділянок місцевості та перешкод (річок, озер, затоплених зон). На рис. 3.9 а показано визначення ширини річки побудовою на місцевості рівнобедреного трикутника. Оскільки в такому трикутнику катети рівні, то ширина річки АВ дорівнює довжині катета АС. Точку А вибирають на місцевості так, щоб з неї було видно місцевий предмет (точка В) на протилежному березі, а також, щоб була можливість вздовж берега виміряти відстань, що дорівнює ширині ріки. Положення точки С визначають методом наближення, вимірюючи кут АСВ компасом чи за допомогою годинника до тих пір, доки його значення не досягне 450.
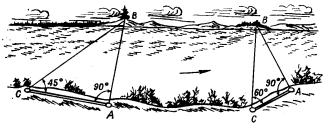
Інший варіант цього способу на рис.3.9 б
Точку С обирають так, щоб кут АСВ дорівнював 600. Відомо, що тангенс кута 600 дорівнює 1/2, отже, ширина річки дорівнює подвоєнному значенню відстані АС. Як і в першому, так і в другому випадку кут при точці А повинен дорівнювати 900.
За тінню від предмета. Для цього необхідно визначити довжину своєї тіні ![]() і довжину тіні Д від предмета. Оскільки трикутники подібні то висоту предмета (дерева) В визначають за формулою:
і довжину тіні Д від предмета. Оскільки трикутники подібні то висоту предмета (дерева) В визначають за формулою:
![]()
де в - зріст людини (спостерігача)
Таким чином висота дерева в стільки разів більше зросту спостерігача у скільки разів тінь від дерева довша його тіні Наприклад довжина тіні спостерігача 3,5 м а тіні від дерева - 24,5 м тобто в 7 разів довша Якщо зріст спостерігача 1,8м то висота дерева 1,8![]() 7=12,6 м
7=12,6 м
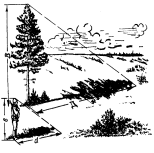 Точність визначення висоти предметів залежить від точності визначення відстані до нього (у першому випадку) або довжини його тіні (у другому випадку)
Точність визначення висоти предметів залежить від точності визначення відстані до нього (у першому випадку) або довжини його тіні (у другому випадку)
Леонардо да Вінчі назвав механіку раєм математичних наук. З не меншим правом так можна назвати й геодезію та картографію. Від простих вимірювань до найскладніших – усім править математика. На основі теорем з курсу шкільної геометрії можливо виміряти висоту вежі, висоту дерева, ширину річки.
Математика в авіації та космонавтиці
Астрономія – наука, що вивчає рух, будову, походження і розвиток небесних тіл і їх систем. Сучасна астрономія тісно пов’язана з математикою і фізикою. Один з розділів математики «тригонометрія» досить довгий час розвивався разом з астрономією і вважався підпорядкованим їй. Використовуючи знання з тригонометрії можна визначити відстань до небесного світила в земних радіусах. Кут, під яким із світила видно радіус Землі, перпендикулярний до променя зору, називається горизонтальним паралаксом. Взявши радіус за одиницю, можна виразити відстань до світила у земних радіусах. Паралаксу Сонця відповідає середня відстань Землі від Сонця, що приблизно дорівнює 150 000 000 км. Цю відстань узято за одну астрономічну одиницю (1 а. о.). В астрономічних одиницях часто вимірюють відстань між тілами Сонячної системи.
Виникнення авіації та космонавтики невідривно пов’язане з застосуванням математики для аналізу основних проблем польоту, конструювання та розрахунку літаків і ракет. Перше питання, яке виникло наприкінці ХІХ – початку ХХ ст. було пов’язане з тим чи зможуть літати апарати, які важчі від повітря. Це питання було вирішено російським вченим, теоретиком авіації М. Жуковським за допомогою теорії функцій комплексної змінної , ним було запропоновано математичну формулу для підйомної сили F= ρvΓ, де р – щільність повітря, v – швидкість рухів крила, Г – так звана циркуляція. Таким чином було дано поштовх розвитку авіації.
Політ літака – це нескінченна шеренга складних математичних задач, які визначають можливі, потрібні й безпечні траєкторії польоту й фігури пілотажу. В 1892 р. М. Жуковський на основі складених ним рівнянь динаміки для центра маси птаха обчислив траєкторії його при різних умовах руху повітря. Між можливими траєкторіями було знайдено і траєкторію у вигляді «мертвої петлі». Так, за 21 рік до того, як російський пілот П. Нестеров практично виконав цю фігуру на літаку в повітрі, Жуковський знайшов її математичну формулу. Перш ніж здійснити «мертву петлю», Нестеров звертався за консультаціє до вченого і той дав йому цінні практичні поради. Тепер «мертва петля» називається петлею Нестерова. Сучасний комплекс фігур найвищого пілотажу складається з 14 елементів. (додаток 9)
Якщо ж взяти до уваги розвиток космонавтики, то слід зупинитись окремо на основоположнику теоретичної космонавтики К. Ціолковському, який в своїх доказах можливості польоту до інших планет і в проектах космічних польотів постійно використовував математику, завдяки чому його космічні проекти були конструктивними та переконливими. Також згадаємо великого математика Р. Декарта, оскільки при виводі космічного апарата на траєкторію польоту і під час його вільного польоту для того, щоб знати де він знаходиться на даний момент використовуються декартові координати точки. Тобто можливість визначення положення тіла в просторі зводиться до математичних дій.
Відомий письменник, популяризатор кібернетики В. Пекеліс писав після запуску першого в світі штучного супутника Землі в статті «Кібернетика і космос»: «Я беру на себе сміливість твердити, що образно кажучи, космічні ракети зроблені не з металу, а з математичних формул, рівнянь і розрахунків». Інакше кажучи з цього робимо висновок, що математика стає основним інструментом для керування польотом космічних кораблів.
ВИСНОВКИ
Чи можливе життя без математики? Цікаве запитання… Суха, нудна наука, яка оперує цифрами, арифметичними діями, у якій чуємо такі страшні слова як «інтеграл», «похідна», «формула», «площа»… Людина, почувши ці визначення, скривиться і скаже: «Та кому воно треба! Живу я без цих інтегралів і ніде вони мені не знадобились!» І буде неправа, бо нещодавно отримала у спадок земельну ділянку, яку перед тим виміряли і обчислили її площу, щоб зафіксувати все це у документах. А тільки що, ця людина переходила міст, який було побудовано за допомогою розрахунків, де застосовувався той самий страшний «інтеграл». Страшно сказати, але сьогодні б ця людина не отримала зарплатні, бо бухгалтер на виробництві не вмів би порахувати відсотки для премії та понаднормові…
Вона навколо нас, вона скрізь, в кожній дрібниці… одиниці вимірювання, чарівна паличка Гаррі Поттера, дедукція Шерлока Холмса, морські карти та прилади піратів, мертва петля Нестерова, політ у космос… Ми живемо з математикою, ми використовуємо математичні знання, навіть якщо про це не здогадуємось. Життя не було б таким цікавим, якби у ньому не було математики!
СПИСОК НАУКОВИХ ДЖЕРЕЛ
1.Військова топографія, Шмаль В. Г., 2013 р.
2. Математика служить людині, Конфорович А. Г., Київ, 1984
3.История математики т. 1, Рыбников К. А., Москва, 1960
4.Символическая логика или безупречная бессмыслица, Кэрролл Л.,
Москва, 2017
5.Записки о Шерлоке Холмсе, Дойль А.К., Киев, 2015
6.Занимательная алгебра, Перельман Я. И., Москва, 1978
7.Колумби математики, Конфорович А. І., Київ, 1982
ДОДАТКИ
Додаток 1

Єгипетський папірус Райнда

Московський математичний папірус
 Додаток 2
Додаток 2
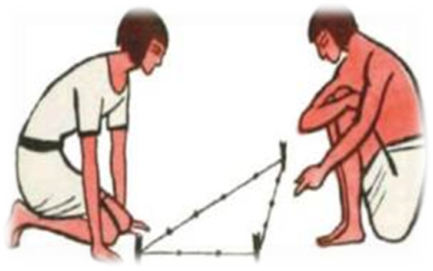

Землеміри-геометри «гарпедонапти» або «ті, що натягують мотузку»
Додаток 3

Додаток 4

Автор «Аліси у країні Чудес» Л.Керрол


Додаток 5


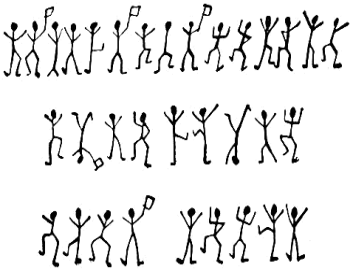
Додаток 6



Математика і судноплавство
Додаток 7




Військова топографія
Додаток 8


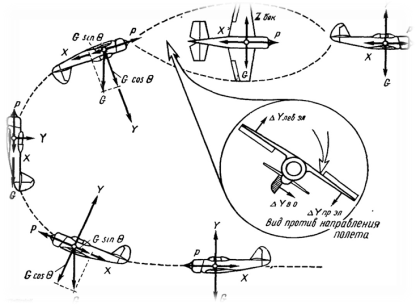
М. Жуковський П. Нестеров
 Додаток 9
Додаток 9
К. Ціолковський

«…Космічні ракети зроблені не з металу,
а з математичних формул, рівнянь і розрахунків»
1


про публікацію авторської розробки
Додати розробку
