Матеріали до уроку "Рівняння площини"

Рівняння площини

Короткий виклад теоретичного матеріалу та приклади розв’язання вправ

Вектор, перпендикулярний до площини, називають вектором нормалі цієї площини. Площина має безліч векторів нормалі, їхні координати пропорційні.

Рівняння площини з вектором нормалі (a; b; c), яка проходить через точку М(x₀; y₀; z₀), має вигляд a(x – x₀) + b(y – y₀) + c(z – z₀) = 0.

Загальне рівняння площини має вигляд ax + by + cz + d = 0, де a, b і c не дорівнюють нулю одночасно, причому вектор (a; b; с) є її вектором нормалі.

Рівняння, площини, що проходить через початок координат:

ax + by + cz = 0, де a, b і c не дорівнюють нулю одночасно.

Рівняння координатних площин:

площини yz:  х = 0;

площини хz:  y = 0;

площини xy:  z = 0.

Рівняння площин, які паралельні координатним площинам:

площині  yz:  х = а;

площині  хz: y = b;

площині  xy: z = с.

Рівняння площин, які паралельні осям координат:

осі х:  by + cz + d = 0;

осі у:  ax + cz + d = 0;

осі z:  ax + by + d = 0.

Рівняння площин, які проходять через осі координат:

вісь х:  by + cz = 0;

вісь у:  ax + cz = 0;

вісь z:  ax + by = 0.

Відстань від точки M (x₀; y₀; z₀) до площини, заданої рівнянням ax + by + cz + d = 0, можна обчислити за формулою

 .

Взаємне розміщення двох площин

Нехай задано дві площини  а₁x + b₁y + c₁z + d₁ = 0  і  a₂x + b₂y + c₂z + d₂ = 0.

Якщо , то площини паралельні.

Якщо , то площини збігаються.

Кут між двома площинами

Нехай задано дві площини  а₁x + b₁y + c₁z + d₁ = 0  і  a₂x + b₂y + c₂z + d₂ = 0.

Двогранний кут  між площинами вимірюється лінійним кутом, який дорівнює куту між векторами нормалі ₁(a₁; b₁; с₁) і ₂(a₂; b₂; с₂) цих площин:

.

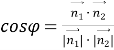Величина кута між площинами має бути в межах від 0 до 90.

Приклади

1. Скласти рівняння площини, яка проходить через точку M(3; -9; 1) перпендикулярно до вектора (2; -1; 3).

Розв’язання. Рівняння площини, яка проходить через задану точку перпендикулярно до заданого вектора, має вигляд а( x  x₀)  b(y  y₀)  с(z  z₀)   0.

Підставимо а  2 , b  -1, с  3 (це координати вектора ),

x₀  3, y₀  -9 , z₀  1 (це координати точки M).

Отримаємо

2(x  3) – 1( y  (9))  3(z 1)  0,

2x  6  y  9  3z  3  0,

2x  y  3z 18  0.

2. Знайти рівняння площини, яка проходить через точку M(2; 2; -2) і паралельна до площини 

x − 2y − 3z = 0.
Розв’язання. Оскільки дві площини паралельні, то вектори нормалі обох площин рівні, знаходимо його з рівняння площині x − 2y − 3z = 0:

(1; -2; -3). Підставимо координати вектора нормалі і точки М в рівняння площини, що проходить через задану точку перпендикулярно заданому вектору a(x – x₀) + b(y – y₀) + c(z – z₀) = 0

і отримаємо

1(x − 2) − 2(y − 2) – 3(z + 2) = 0

або x − 2y − 3z – 4 = 0.

3. Записати рівняння площини, що проходить:

1) паралельно пло­щині хz і через точку (2; -5; 3);

2) через вісь z і точку (-3; 1; -2);

3) паралельно осі х і через точки (4; 0; -2) і (5; 1; 7).

Розв’язання. 1) Рівняння шуканої площини у = b. Точка (2; -5; 3) лежить у площині, тобто задовольняє це рівняння; маємо: у = -5, або у + 5 = 0.

2) Рівняння шуканої площини ах + bу = 0. Підставимо координати точки (-3; 1; -2) в це рівняння. Отримаємо -3а + b = 0, звідки b = 3а.

Підставимо b = 3а в рівняння ах + bу = 0. Тоді маємо ах + 3ау = 0. Поділимо рівняння на а (згідно умови а  0). Тоді рівняння шуканої площини має вигляд х + 3у = 0.

3) Рівняння площини, паралельної осі х, має вигляд: by + cz + d = 0.  

Підставляючи в нього почергово координати точок (4; 0; -2) і (5; 1; 7), дістаємо систему

Звідки d = 2c, b = -9c. Підставимо ці значення в рівняння by + cz + d = 0:

-9су + сz + 2c = 0 | : c  0 (згідно умови)

-9y + z + 2 = 0 або 9у – z – 2 = 0.