Матеріали до заняття з математики для 6-го класу "Перпендикуляр, що проходить через середину відрізка та його властивості." (план-конспект, презентація, тест самоконтролю)
Запропоновану розробку доцільно використовувати для самостійного ознайомлення учнів 6-го класу з навчальним матеріалом.
Тема заняття «Перпендикуляр, що проходить через середину відрізка та його властивості.
Мета заняття: Сформувати поняття про перпендикуляр, серединний перпендикуляр до відрізка; познайомити з властивостями серединного перпендикуляра; формувати вміння будувати серединний перпендикуляр до відрізка; навчити застосовувати здобуті знання до розв'язування задач на побудову.
Алгоритм роботи з матеріалом заняття
1.Прочитати теоретичні відомості про перпендикуляр, серединний перпендикуляр
2.Ознайомитись з алгоритмом побудови серединного перпендикуляра
3.Розглянути приклади розв'язування задач
4.З метою самоперевірки відповісти на контрольні питання та виконати тестові завдання
- ßἫ¬«¡Γα«½ε.doc doc
- .ppt ppt
- Pryklady.doc doc
- Text.doc doc
- Показати всі файли
Тест самоконтролю до заняття
Початковий рівень
- Через задану точку до прямої можна провести…
- безліч перпендикулярів
- три перпендикуляри
- єдиний перпендикуляр
- чотири перпендикуляри
- Що називають відстанню від заданої точки А до прямої а?
- Будь-яку пряму, проведену з точки А до прямої а
- Її не можна визначити однозначно
- Відстань від точки А до середини перпендикуляра
- Довжину перпендикуляра, проведеного з точки А до прямої а
Середній рівень
-
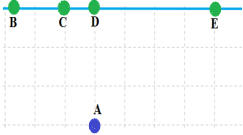 В точці А знаходиться табір літнього відпочинку. На березі річки кілька пляжів: В, С, D та Е. Яка з доріг веде до найближчого пляжу?
В точці А знаходиться табір літнього відпочинку. На березі річки кілька пляжів: В, С, D та Е. Яка з доріг веде до найближчого пляжу?
- АВ
- AD
- АЕ
- АС
-
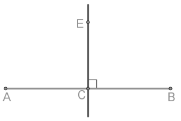 Задано: відрізок АВ та CE — серединний перпендикуляр до відрізка AB. Визначити довжину AB, якщо BC= 48 см.
Задано: відрізок АВ та CE — серединний перпендикуляр до відрізка AB. Визначити довжину AB, якщо BC= 48 см.
- 24 см
- 48 см
- 96 см
- 72 см
-
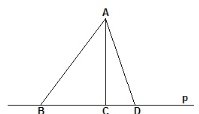 Який з відрізків АВ, АС чи AD є перпендикуляром до прямої р?
Який з відрізків АВ, АС чи AD є перпендикуляром до прямої р?
- жоден
- АС
- AD
- АВ
-
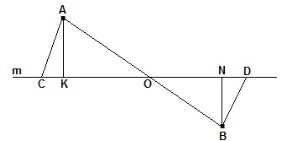 З точок А та В, що не належать прямій m. Визначте, які прямі побудовано перпендикулярно до прямої m
З точок А та В, що не належать прямій m. Визначте, які прямі побудовано перпендикулярно до прямої m
- АО та ВО
- АС та ВD
- АК та ВN
- CK та DN
-
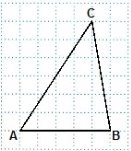 Задано трикутник АВС. Знайдіть відстань від точки В до сторони АС
Задано трикутник АВС. Знайдіть відстань від точки В до сторони АС
- 2 см
- 2,5 см
- 3 см
- 1,5 см
- Що визначає розміщення точок, рівновіддалених від заданих точок А, В?
- середина відрізка АВ
- серединний перпендикуляр до відрізка АВ
- трикутник з основою АВ
- коло з діаметром АВ
-
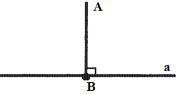
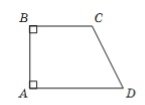 На рисунку BC⊥AB, AD⊥AB. Назвіть відрізок, який визначає відстань від точки C до прямої AB
На рисунку BC⊥AB, AD⊥AB. Назвіть відрізок, який визначає відстань від точки C до прямої AB
- ВС
- АD
- CD
- AB
Високий рівень
- На прямокутній системі координат побудовано відрізок АВ: А (-13; 4), В (5; 4). Визначити координати точки, через яку проходить серединний перпендикуляр до цього відрізка
- (0; 4)
- (1; 5)
- (-4; 7)
- (4; 6)
-
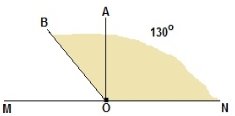 До прямої MN проведено перпендикуляр АО.
До прямої MN проведено перпендикуляр АО. 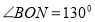 . Знайдіть кути
. Знайдіть кути 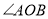 та
та 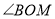
- 40о; 50о
- 30о; 60о
- 20о; 70о
- 140о; 150о
Приклади вирішення та оформлення завдань до уроку
«Перпендикуляр, що проходить через середину відрізка та його властивості»
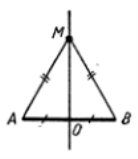
Приклад 1. Доведіть, що кожна точка, яка рівновіддалена від кінців відрізка, належить його серединному перпендикуляру
|
|
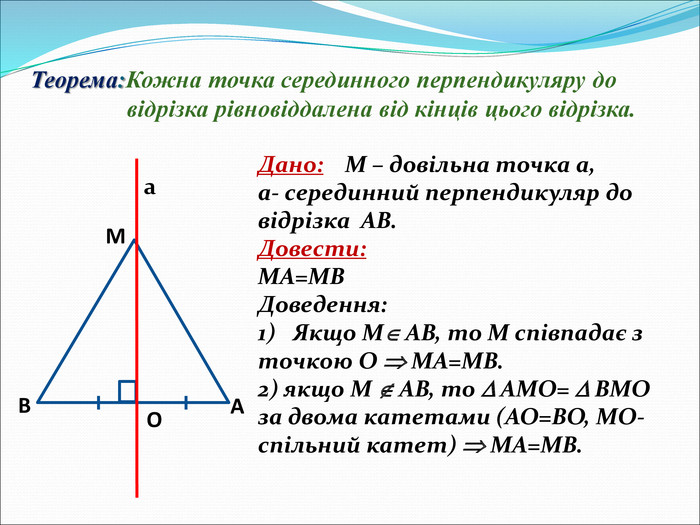
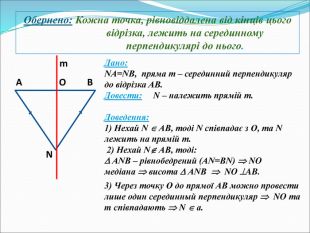
Дано: відрізок АВ,
АМ = ВМ АО = ВО Довести: МО – серединний перпендикуляр
|
Доведення
Якщо точка М належить прямій АВ, то вона співпадає з серединою О відрізка АВ, а отже, лежить на його серединному перпендикулярі.
Якщо точка М не належить прямій АВ, то маємо рівнобедрений ![]() , бо АМ = ВМ (за умовою). Відрізок МО – медіана цього трикутника, а отже, його висота. Тобто:
, бо АМ = ВМ (за умовою). Відрізок МО – медіана цього трикутника, а отже, його висота. Тобто: ![]() .
.
Таким чином, пряма МО, якій належить точка М, є серединним перпендикуляром відрізка АВ.
Доведено
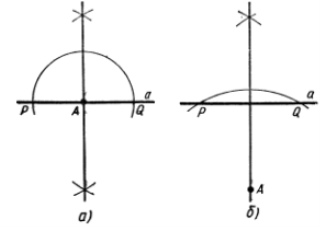
Побудова за допомогою циркуля
Приклад 2. Побудувати пряму, яка проходить через задану точку А, перпендикулярно до заданої прямої а
|
|
Дано: відрізок а, точка А Побудувати: перпендикуляр через точку А до прямої а
|
Побудова
З метою виконання необхідної побудови важливо відмітити, що існують два випадки розв’язування, в залежності від розміщення точки А відносно прямої а:
-
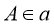 ;
;
-
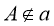 .
.
Однак, незалежно від розміщення точки А, розв’язок базується на побудові серединного перпендикуляру.
Побудуємо коло з центром у точці А, яке перетинає пряму а у будь-яких двох точках P та Q. З того, що АP = АQ маємо рівновіддалену точку А від кінців відрізка PQ. Тобто, точка А належить серединному перпендикуляру цього відрізка. Будуємо серединний перпендикуляр до відрізка PQ, який є прямою, що проходить через точку А, перпендикулярно до заданої прямої а.
План-конспект заняття
|
№ з\п |
Матеріали плану-конспекту заняття |
|
1 |
Тема заняття 9 «Перпендикуляр, що проходить через середину відрізка та його властивості» |
|
2 |
Мета заняття: Сформувати поняття про перпендикуляр, серединний перпендикуляр до відрізка; познайомити з властивостями серединного перпендикуляра; формувати вміння будувати серединний перпендикуляр до відрізка; навчити застосовувати здобуті знання до розв’язування задач на побудову |
|
3 |
Алгоритм роботи з матеріалом заняття
|
|
4 |
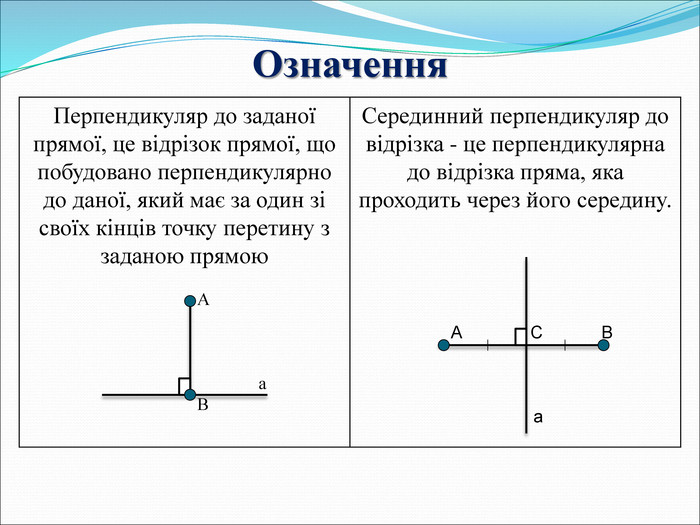
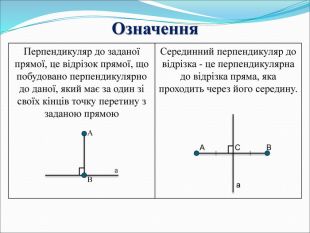
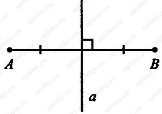
Теоретичні відомості Перпендикуляр до даної прямої, це відрізок прямої, що побудовано перпендикулярно до даної, який має за один зі своїх кінців точку перетину з даною прямою (рис.1)
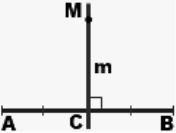
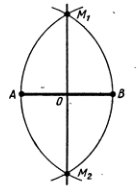
Рис.1 Довжина перпендикуляра, проведеного з заданої точки до прямої, називається відстанню від цієї точки до цієї прямої. Серединний перпендикуляр до відрізка – це перпендикулярна до відрізка пряма, яка проходить через його середину (рис.2)
Рис.2 |
|
5 |
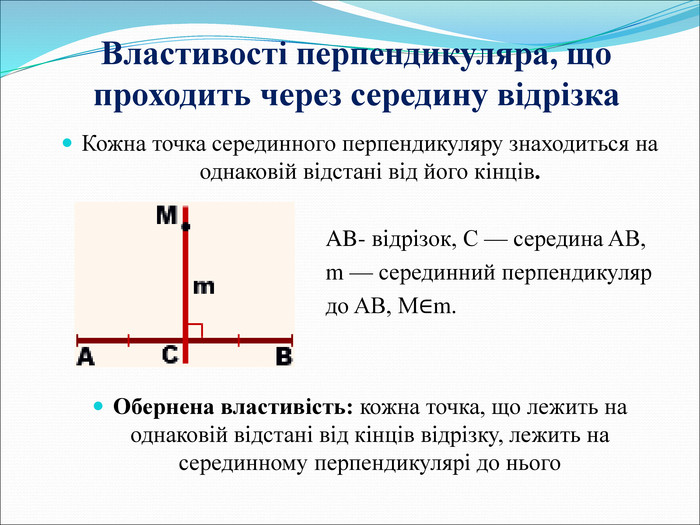
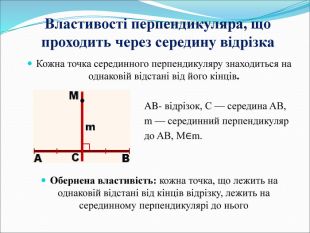
Додатковий матеріал для «розумників» Властивості перпендикуляра, що проходить через середину відрізка: Теорема: Кожна точка серединного перпендикуляру знаходиться на однаковій відстані від його кінців (рис.3)
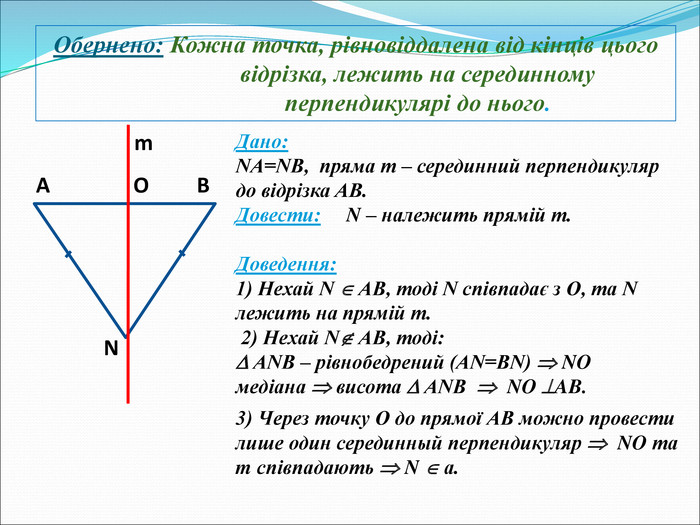
Рис.3 Обернена теорема: кожна точка, що лежить на однаковій відстані від кінців відрізку, лежить на серединному перпендикулярі до нього Алгоритм побудови серединного перпендикуляра до відрізка:
Рис.4 |
|
6 |
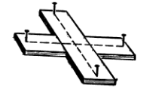
Практичне застосування серединного перпендикуляра: Побудова прямих кутів на місцевості Для побудови прямих кутів на місцевості використовують спеціальні прилади, найпростішим з яких є екер (рис.5). Екер складається з двох брусків, які розміщені один до одного під прямим кутом та закріплені на тринозі. На кінцях брусків насаджені шпильки таким чином, що прямі, які проходять через них, взаємно перпендикулярні.
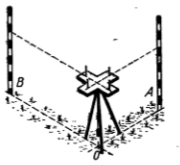
Рис.5 З метою побудови на місцевості прямого кута із заданою стороною ОА, встановлюють триногу з екером так, щоб схил знаходився точно над точкою О, а напрям одного з брусків співпадав з напрямом променя ОА. Суміщення цих напрямів здійснюється за допомогою віхи, яка розміщується на промені. Після чого відбувається проведення прямої лінії у напрямку іншого брусу (пряма ОВ на рис.6). Одержується прямий кут АОВ
Рис.6
|
Відповіді до тесту самоконтролю до заняття
Ключ до тесту:
|
№ заняття |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Відповідь |
В |
Г |
Б |
В |
Б |
В |
А |
Б |
А |
В |
А |
|
Кількість балів |
0,5 |
0,5 |
0,5 |
0,5 |
1 |
1 |
1 |
1 |
1 |
2 |
3 |
Рекомендації, для подальшої роботи з курсом:
- Якщо результат проходження тесту для самоконтролю становить 10-12 балів, то здійснюється перехід до наступного заняття
- Якщо результат проходження тесту для самоконтролю становить менше 10 балів, то потрібно повернутися назад до вивчення матеріалу заняття № 9


про публікацію авторської розробки
Додати розробку