Майстер - клас учителя початкових класів НВК «Гімназія – школа» № 27 м. Маріуполя Сахарової Н.Є. «Розвиток логічного та просторового мислення учнів початкових класів на уроках мате

Про матеріал

Майстер - клас «Розвиток логічного та просторового мислення учнів початкових класів на уроках математики та спецкурсі «Основи геометрії» є представленням досвіду роботи вчителя початкових класів Сахарової Н.Є., містить теоретичні, практичні наробки, які є ефективними на уроках.

Перегляд файлу

Опис досвіду

учителя початкових класів НВК «Гімназія – школа» № 27 м. Маріуполя

Сахарової Наталії Євгенівни

«Розвиток логічного та просторового мислення учнів початкових класів на уроках математики та спецкурсі «Основи геометрії».

Ми занадто часто даємо дітям відповіді,

які треба вивчити, а не ставимо

перед ними проблеми, які треба вирішити.

Роджер Левін

Ніколи ще до нашого часу ми не жили в такий геометричний період.

Навколишній світ – це світ геометрії, чистий, істинний,бездоганний

у наших очах. Усе навколо – геометрія.

Ле Корбюзьє

(найвідоміший архітектор ХХст.)

У зв’язку з і змінами в системі освіти України, які відбулися на порозі нового тисячоліття, найактуальнішим питанням на сьогоднішній день, згідно з Концепцією 12 – річної школи, стало питання всебічного розвитку дитячої особистості, на основі реалізації її природних можливостей, врахування інтересів і потреб.

Математика в початковій школі - це одна з найважливіших дисциплін. Вона розвиває уяву, спостережливість, образне й логічне мислення, яке є основою творчості, складовою частиною інтуїції, без якої не обходиться жодне наукове відкриття. Саме на уроках математики формуються особисті якості дитини: зібраність, організованість, здатність швидко та якісно приймати рішення, доводити й відстоювати свою думку.
Зважаючи на те, що основною метою сучасної школи, як зазначає О. Я. Савченко, є підготовка учнів до життя, до суспільно – корисної праці, особливої ваги слід надавати тим питанням програми, з якими її вихованці не раз зустрічатимуться у своїй життєдіяльності, і одним з цих питань курсу математики є вивчення геометричного матеріалу.

Практика навчання такого предмету, як , геометрія, показує, що до 12-13 років багато дітей не володіють прийомами уявного перетворення просторових образів.

Змінити цю ситуацію може тільки систематичне навчання дітей початкових класів за спеціально підібраним геометричних завдань на розвиток логічного мислення і просторової уяви.

Необхідність формування просторової уяви обумовлена трьома причинами: математичної, фізіологічної та психологічної.

З математичної точки зору, навчання молодших школярів геометрії є пропедевтикою для вивчення систематичного курсу геометрії в основній та старшій школі.

З точки зору фізіології, вивчення геометрії сприяє розвитку правої півкулі головного мозку, що відповідає за здатність людини оперувати образами.

На думку фізіолога І. Соньер «навчаючи ліву півкулю, ви навчаєте ліву півкулю; навчаючи праву півкулю, ви навчаєте весь мозок!»

Саме права півкуля пов'язана з розвитком творчого мислення, вмінням орієнтуватися в просторі, що є необхідним компонентом будь-якого виду навчальної діяльності.

Психологічна причина - учні початкових класів повинні швидко перебудувати свою структуру психічних операцій і вчитися мислити в площині.

Згідно з Державним стандартом початкової освіти з метою виховання неординарної особистості з нестандартним мисленням, розвитку її талантів, здібностей, компетентностей самостійності, творчості та допитливості з 2010 року, мною був апробований курс "Елементи геометрії" для учнів 4 класів , де особливу увагу приділяю не тільки питанням розвитку просторового мислення але й розвідку інтелектуальних і творчих здібностей, розвитку математичної мови, яка є однією з умов формування комунікативних компетентностей учнів.

Таким чином основні завдання спецкурсу «Основи геометрії»:

1) розвинути просторові уявлення дітей;

2) сформувати у молодших школярів правильні уявлення про найпростіші геометричні фігури (точка, пряма, крива, відрізок, ламана, кут, многокутник, круг, коло, многогранники, круглі тіла) та їх найпростіші властивості;

3) навчити учнів розпізнавати та розрізняти вказані фігури серед інших геометричних об’єктів;

4) сформувати у дітей уміння зображати визначені програмою геометричні фігури;

5) навчити школярів знаходити довжину ламаної, відрізка, периметр і площу многокутника;

6) сформувати в учнів навички користування вимірювальними та креслярськими інструментами;

7) навчити дітей виконувати елементарні геометричні побудови та дати уявлення про точність побудов і вимірювань;

8) розвивати у школярів уміння спостерігати, порівнювати, аналізувати, абстрагувати, узагальнювати тощо;

9) нагромадити в учнів запас геометричних уявлень, яких буде достатньо для вивчення систематичного курсу геометрії;

10) розвивати у школярів логічний та інтуїтивний компоненти мислення тощо.

Програму побудовано за блочним принципом. Змістове наповнення розділів програми складають теми:

Готуючись до пояснення певного поняття, мною було проаналізовано:

що відомо про це поняття з попередніх уроків математики в школі;

що школярі повинні вивчити про це поняття зараз;
як це поняття з часом буде ускладнюватися в початковій школі і на який рівень знань про нього діти повинні вийти, закінчивши початкову школу;
як це поняття трактується в 5-6 класах та в систематичному курсі геометрії.

Програмні вимоги щодо рівня геометричних знань з математики початкової школи таких авторів: Ф.М.Рівкінд, Л.В.Оляницька.

Назви геомет ричних об’єктів	Рівень знань
Назви геомет ричних об’єктів	1 клас	2 клас	3 клас	4 клас	Спецкурс «Основи геометрії»
1. Лінії	Пряма. Крива. Ламана.	Пряма. Крива. Ламана.Вертикальні і горизонтальні лінії.	Замкнена, незамкнена ламана. Довжина ламаної.	Замкнена, незамкнена ламана. Довжина ламаної.	Перпендикулярні і паралельні прямі.
2.Точка, відрізок, промінь, пряма.	Точка, відрізок, промінь.	Точка, відрізок, промінь, пряма.	Точка, відрізок, промінь, пряма.Вертикальні, горизонтальні та похилі відрізки.	Точка, відрізок, промінь, пряма.Вертикальні, горизонтальні відрізки.	Система координат.Будова фігур за координатами.
3. Кути.	-	Прямий кут.	Кути. Елементи кутів.	Кути. Елементи кутів.	Види кутів. Градусна міра кутів. Побудова трикутників за його елементами.
4.Трикут ник, чотири-кутник, многокут-ники.	Трикутник, чотирикутник, многокутники.	Елементи многокутників. Периметр.	Елементи многокутників. Периметр.Побу-дова трикутників за зразком.	Периметр і площа квадрата і прямокутника.	Класифікація трикутників(за кутами та сторонами).Медіана, бісектриса, висота трикутника.
5. Коло і круг	Коло і круг.	Радіус, діаметр кола. Побудова кола даного радіуса.	Радіус, діаметр кола. Побудова кола даного радіуса.	Радіус, діаметр кола. Побудова кола даного радіуса.	Ознайомлення з поняттям «хорда», «діаметр», «сектор», «сегмент» круга.
6.Просто-рові тіла.	Ознайомлення з формами і назвами основних геометричних тіл.	Просторові тіла.	Просторові тіла.	Просторові тіла.	Геометричні тіла , їх елементи. Побудова.

Такий аналіз дозволяє вивчати поняття з урахуванням принципу наступності: допомагає правильно активізувати попередні знання, визначить, що нове потрібно пояснити, коли і як це нове ускладниться, розкриває пропедевтичні можливості матеріалу.

До програми спецкурсу розроблено мультимедійний супровід у формі презентацій.

Методика використання мультимедійних технологій у процесі вивчення матеріалу сприяє наступному:

- посиленню мотивації навчання учнів;

- вдосконаленню системи управління навчанням на різних етапах уроку;

- зростанню якості навчання і виховання, підвищенню інформаційної культури учнів;

- підвищенню рівня обізнаності учнів щодо сучасних інформаційних технологій;

- демонстрації можливостей комп'ютера не лише як засобу для гри.

Уроки з мультимедійним супроводом допомагають ефективно вирішувати наступні дидактичні завдання:

- сформувати мотивацію до навчання взагалі;

- засвоїти базові знання з предмета;

- сформувати навички самоконтролю.

Розроблений дидактичний матеріал для учнів та методичні рекомендації для вчителя. Його мета – викликати цікавість учнів початкової школи до вивчення геометрії як невід’ємної складової математичної освіти.

Дидактичний матеріал для учнів та методичні рекомендації для вчителя включають систему пізнавальних статей, творчих, ігрових та нестандартних завдань, спрямованих не лише на розвиток загально-навчальних умінь та навичок, а й набуття молодшими школярами досвіду пошукової, конструкторської діяльності, розвитку інтуїції, навичок мислення, тобто сприяє підвищенню їх інтелектуального рівня.

Вивчення геометричного матеріалу необхідно супроводжувати практичними вправами, при цьому учні сприймають не лише готові геометричні фігури і тіла, вони самостійно створюють і відтворюють досліджувані геометричні форми, використовуючи для цього вирізання, моделювання, склеювання, креслення, конструювання .

Отримані знання використовуються дітьми на практиці не тільки на уроках математики, а також на уроках праці, мистецтва, на уроках природознавства.

Окрім знань предмету, сучасних дітей потрібно постійно зацікавлювати.

Універсальні способи, які мені допомагають при підготовці до уроку.

Почніть урок з того , що здивує дітей. Спробуйте сказати щось, що здивує: незвичайний факт разюче повідомлення.

Шукайте зв'язки. Завжди намагаюся пов'язати свою тему з іншою дисципліною, природним явищем.

Міжпредметні – це спосіб показати, що все у світі взаємопов'язане.

Створюйте уявні проблеми. Запропонуйте щось, що змусить задуматися. Суперечливі питання, які і надихне, і спонукає шукати варіанти відповіді.

Комбінуйте різні методи подачі інформації. На уроці йдемо до однієї мети, і як знаємо, в геометрії Евкліда найкоротший шлях-це пряма, але найкоротший не завжди найефективніший і цікавий. Іноді краще йти в обхід. Зміна видів діяльності тримає учнів в тонусі.

Адаптуйтесь. В ході уроку можуть виникнути питання . Треба бути готовим відповісти на них або розгорнути навколо нього дискусію.

Використання ІНФОРМАЦІЙО – КОМУНІКАЦІЙНИХ ТЕХНОЛОГІЙ – невід’ємна частина сучасної освіти.

Для формування інформаційної компетенції використовую:

Різні форми роботи з підручником;
Використання комп'ютерних навчальних програм, виконання віртуальних практичних робіт, використання відеоматеріалів;
Створення презентацій до уроку (як випереджальне завдання і як узагальнення вивченого матеріалу);
Пошук матеріалів у мережі Інтернет за заданими питаннями, темами;
Комп'ютерне тестування ;
Обмін інформацією з учнями через Інтернет.

Велика роль в сучасному процесі освіти відводиться організації ПРОЕКТНОЇ ДІЯЛЬНОСТІ УЧНІВ, що на сьогодні немислимо без ЗАСТОСУВАННЯ КОМП'ЮТЕРНИХ ТЕХНОЛОГІЙ. Пропоновані проектні завдання розраховані на виконання в малих групах (2-3 людини). Кожна група отримує завдання. Групи працюють одночасно і незалежно один від одного. Для ознайомлення з результатами діяльності інших груп після закінчення вивчення теми влаштовується конференція. У навчальні програми включені обов'язкові навчальні проекти).

У своїй роботі періодично використовую МЕТОД ПЕРЕВЕРНУТОГО НАВЧАННЯ. Модель перевернутого класу дозволяє:

скоротити час на пояснення матеріалу за рахунок домашнього знайомства з теорією (перегляд відео, спільна робота учнів за допомогою ІКТ, робота із заздалегідь наданими вчителем опорними конспектами);
здійснити індивідуальний підхід за рахунок того, що засвоювати теорію кожен учень може в своєму темпі, є можливість багаторазово до неї повернутися;
використовувати на уроці діяльнісний підхід, завдяки економії часу на вивчення теорії на уроці.

Прийоми роботи з текстами теоретичного змісту:

Прийом «Читання з позначками».

Я це знав

Нове для мене

Я думав інакше

Цікаво

Незрозуміло

Потрібно розібратися

У результаті в учнів розвивається допитливість, пізнавальний інтерес, уміння зосереджуватися, мислити самостійно, формуються вміння, необхідні для життя в соціумі.

На уроках використовую ІГРОВІ ЗАВДАННЯ:

Логічні ланцюжки;
Знайти помилку;
Знайти пару;
Дізнайся об'єкт;
Лабіринти;
т.д.

Створення ігрових ситуацій призводить до швидкого і доступного засвоєння знань і умінь. Під впливом захопленості навіть важкий матеріал засвоюється легше і успішніше. Гра сприяє розвитку творчого потенціалу учнів, їх уваги, пам'яті, уяви та мислення, а це в свою чергу впливає на навчальну діяльність і результати навчання.

Приклади:

Проведіть по лабіринту незамкнену криву лінію, яка покаже мишці шлях до сиру.

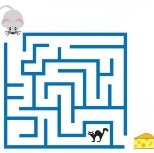
labirintydlyadetey17 300x300 Лабиринты для детей

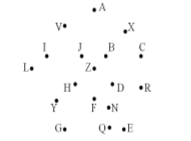
Спробуй знайти спосіб, щоб прочитати приказку.

З’єднайте точки за назвами відрізків: АВ, ВС, СD, DE, EF, FG, GH, HI, IJ, JА. Яку фігуру отримали?

Логічні вправи «Веселі палички»

1.Викласти з паличок слова і визначити кути :

а) Слово « КУТИ» . У якій з букв є 2 гострі кути? У якій є гострий, тупий та розгорнутий кути?

б) Слово «ТАНК». У якій із букв у слові є 4 прямих кути?

в) Слово «БУРУН» . У якій букві найбільше прямих кутів?

Порахуйте, скільки кутів «сховалося» в слові КУТ. Назвіть види цих кутів.

2.Який кут – гострий, прямий чи тупий – утворюють стрілки кожного з поданих годинників?

Побудова фігур за заданими координатами.

У стародавніх греків існувала легенда про сузір'я Великої і Малої Ведмедиць. Всемогутній бог Зевс вирішив взяти собі в дружини прекрасну німфу Калісту, одну із служанок богині Афродіти, всупереч бажанню останньої. Щоб позбавить Калісту від переслідувань богині, Зевс звернув Калісту у Велику Ведмедицю, а її улюблену собаку-в Малу Ведмедицю, взявши їх на небо.

(6;6),(-3;5,5), (-8;5), (0;7,5), (3;7), (-5;7), (-6;3)(-15;-7), (-3;-6), (5;10), (-6;-5,5), (-10;-5), (6;-6),

(-1;-10)

Що отримали?

Творчі завдання.

1.Поділити трикутники(рівносторонні):

1)трьома лініями на 4 рівні частини;

2)трьома лініями на 6 рівних частин;

3)однією лінією на 4 частини, причому три з них рівні між собою.

2.Зображений многокутник «розріж» на трикутники. Скільки отримав трикутників?

Розмальовки.

1.Всі трикутники розфарбуй жовтим кольором, багатокутники – зеленим.

2.Трикутники - коричневим кольором, багатокутники – жовтим. Що вийшло?

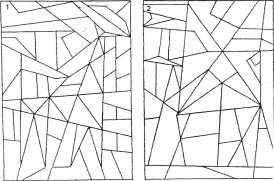
Загадки.

Три у мене сторони, міцно з`єднані вони.

А між ними три кути, хто я? Чи вгадаєш ти? (Трикутник.)

Ось вам загадка непроста: не маю жодного кута!

Фігура я геометрична, така кругленька, симпатична.(Круг.)

Чотири в мене сторони, усі однакові вони.

Всі четверо кутів прямі, ім`я моє назвіть самі. (Квадрат.)

«Хвилинка-цікавинка»

1.«Квадратні» дива природи.

Квадратні кавуни винайшли японці років сорок тому. Точніше, не квадратні, а кубічні. Винахідливі японські фермери здогадалися зростаючий кавун укладати в прозору тару, щоб, виростаючи, плід брав її форму. Кавуни такої форми легко складати, вони займають менше місця, та ще й не катаються по прилавку або на полиці у холодильнику.

Вирощують «квадратні » помідори в Ізраїлі.

На замовлення авіакомпанії генетики США вивели сорт кукурудзи з «квадратними» зернами. Під час «повітряних» обідів у польоті вона не скочується з тарілок.

2.Побачити в навколишньому світі ромб складніше, ніж круг або трикутник, однак це можливо. Причина цього може бути в тому, що він виявляється в самих несподіваних і незвичайних місцях.

3.Трапеція – священна фігура піфагорійців. У кожному домі обов’язково було що-небудь «трапеційне», яке захищало членів родини від усіх бід і негараздів. У нас є «священна» картина тих часів. Покажіть, де на ній зображено трапеції і порахуйте скільки їх.

$C:\Users\User\Desktop\фото школа\Photo1753.jpg$

Складіть трапецію із квадрата і прямокутного трикутника.

г)

Гра «Танграм»

Танграм – надзвичайна гра-головоломка. Так, поєднавши відповідним чином всього 7 фігурок-танів, можна скласти практично будь-яку фігуру (так можна скласти будь-яку літеру абетки, тварин, цифри, силуети людей та ін.).

Принцип гри: Необхідно всередину білого контура вмістити всі 7 фігур таким чином, щоб вони не накладалися одна на одну.

Чи цікаво вам дізнатися чому дорівнює сума усіх кутів трикутника?

Якщо у будь - якому трикутнику відірвати кути і скласти вершинами так, щоб сусідні сторони співпали, то переконаєшся, що всі кути трикутника утворюють розгорнутий кут (180°)

Давайте розглянемо, як можна ефективно вивчити і зафіксувати в пам`яті певну інформацію.

Так звана «Піраміда засвоєння інформації» дає розуміння того, яку ефективність мають різні способи отримання знань.

Незважаючи на те, що прослуховування лекцій відноситься до найбільш неефективного методу навчання, читання лекцій в якості викладача є продуктивним способом засвоїти конкретний матеріал.

Я завжди на уроках намагаюся використовувати і лекцію і читання правил практику через дію вона дає більш ефективно вивчити і зафіксувати в пам`яті певну інформацію.

Вивчення геометричного матеріалу на уроках математики дало мені широкі можливості для розвитку розумових здібностей молодших школярів, а саме сприймання пам'яті, мислення, уваги. Допомогло мені навчити своїх учнів доказово міркувати та пояснювати власні дії, логічно мислити та знаходити вихід із будь-якої ситуації як самостійно, так і в процесі взаємодії зі своїми однокласниками та зі мною як учителем. У свою чергу, це створило позитивні умови для реалізації наступності у вивченні геометрії як систематичного курсу.

Результативність досвіду виражається в стабільній активності учнів, сприятливій творчої атмосфери на уроці. Але основними показниками результативності педагогічного досвіду є:

стабільна якість знань і успішність навчання учнів математики. Протягом 2011-2019 навчальних років стабільно якість знань учнів з математики знаходиться на достатньому рівні.

Щорічно мої учні беруть участь у Всеукраїнських інтерактивних математичних конкурсах, у міських та шкільних олімпіадах, де показують досить високі результати.

Таким чином, можна зробити висновок, що моя система роботи дозволяє вирішити завдання:

підвищити мотивацію до вивчення математики;
підвищити інтерес до процесу навчання і активного сприйняття навчального матеріалу з предмета;
сприяє формуванню інформаційної грамотності: розвитку здатності до самостійної аналітичної та оцінної роботі з інформацією будь-якого виду і різного типу складності;
створює умови для підвищення соціальної компетентності.

При цьому підході крім знань і вмінь учнів важливим показником якості навчання стає наявність у них досвіду вирішення життєвих проблем, соціальних функцій, практичних навичок діяльності.

Свій майстер клас я хочу закінчити словами: «Хоча вчитель - це масова професія ... по суті, вчительська праця є творчою працею. Вона не піддається ніяким правилам або обмеженням за своєю суттю, але, разом з тим, вчителі, як і великі художники, поряд з творчістю, і хороші ремісники. Потрібно володіти основами ремесла, щоб потім ставати великими художниками».

docx

Завантажити

Зберегти на потім

Додав(-ла)

Сахарова Наталія Євгенівна

Пов’язані теми

Математика, 4 клас, Майстер-класи

Додано

12 січня 2020

Переглядів

1063

Оцінка розробки

Відгуки відсутні