Майстер-клас"Розвито логічного мислення на уроках математики"

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ХМЕЛЬНИЦЬКИЙ СПОРТИВНИЙ ЛІЦЕЙ

 

 

 

 

РОЗВИТОК ЛОГІЧНОГО МИСЛЕННЯ

 

 НА УРОКАХ МАТЕМАТИКИ

 

 

 

 

 

Вчитель математики:

Невмержицька Валентина Петрівна

 

 

 

 

 

 

 

 

 

 

г.Хмельницький 2022р.

«Математика належить до числа наук, що мають велике значення для відпрацювання вміння логічно мислити, робити узагальнення»

 Колмагоров

Основною метою математичної освіти у школі є розвиток уміння логічно й усвідомлено досліджувати явища реального світу. Реалізація цієї мети сприяє використанню на уроках математики різного роду нестандартних логічних задач, вправ та методик . Тому розвиток вчителем на уроках математики різних видів логічного мислення є не тільки бажаним ,але навіть необхідним елементом навчання в математиці.

Вчителі стурбовані тим ,що що школярі насилу засвоюють навчальний матеріал, не можуть застосовувати знання в різних життєвих ситуаціях , вибрати той чи інший метод розв’язку проблеми, завдання, учні не вчать правила , не уміють застосовувати їх, не можуть вивчити звичайну теорему.

Ніхто не буде сперечатися з тим, що кожен учитель повинен розвивати логічне мислення учнів. Про це говориться в методичній літературі, у пояснювальних записках до навчальних програм. Однак, як це робити, учитель не завжди знає. Як наслідок - розвиток логічного мислення значною мірою йде стихійно, тому більшість учнів, навіть старшокласників, не володіє основними прийомами логічного мислення. Тому, починати розвивати логічне мислення дітей потрібно вже під час навчання в дитячому садку, бо потім (в старших класах школи) буде важко надолужити те, що втрачено, зробити мислення дітей нестандартним, навчити їх міркувати самостійно.

ПРИТЧА

----Наказую,- мовив Владика,-написати мені все про математику.Як вона виникла, якою була раніше,якою стала тепер, якою беде в майбутньому.Зібрати мені всу математичні завдання, що є в світі, а найголовніше ,дайте відповідь на питання-що це…. МАТЕМАТИКА?

І дав на це 5 років терміну.

….Ледве сонце зійшло на лазурному небі , як Владика зажадав до себе мудреця. Мудрець увійшов, несучи в руках маленьку скриньку із сандалового дерева.

-Ти знайдеш що в ньому , о Владико, найголовніше в математиці всіх часів і народів,- сказав мудрець. Але перш , ніж відкриємо та прочитаємо ,що там написано, я пропоную вам кілька завдань, які можуть викликати подив. Хто знає,  може вони були записані в тих товстелезних томах.

ДИВУЄМОСЬ!!!!!!!

Ми з вами сьогодні поговоримо про логічне мислення.

ЛОГІЧНЕ МИСЛЕННЯ формуємо , використовуючи:

• Різні методики
• Усний рахунок
• Розв’язування вправ та задач різними способами

1.Методика Нікітіних

Методика Нікітіних сприяє повноцінному розвитку дітей, базується на різноманітних іграх із кубиками, цеглинками, квадратами, конструкторами. Вона загальнодоступна, і кожен може її використовувати.
Завдання даються в різній формі:

• у вигляді малюнка;
• у вигляді моделі;
• у вигляді креслення;

 

 

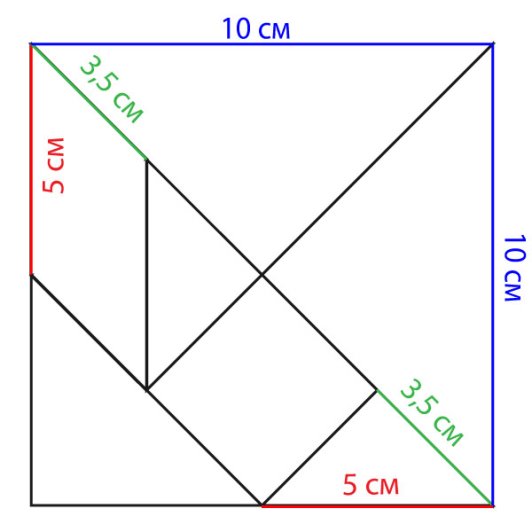
2.Танграм

  Танграм- це головоломка, яка складається з семи гральних кісток — пласких геометричних фігур, які називають танами, що складаються у різні форми. Завдання головоломки — створити задану форму (на підставі лише обрису силуету) з використанням всіх семи танів, які заборонено накладати один на один. Це одна з найбільш популярних головоломок такого типу у світі. Китайський психолог назвав танграм «найдавнішим психологічним тестом світу», хоча і створеним для розваги, а не для аналізу.

  Згідно з легендою, одного разу чернець завдав своєму учню задачу здійснити подорож для того, щоб намалювати суть різноманітної краси світу тільки на одній керамічній дощечці. На жаль, дощечка розбилася на сім шматків і учень ніяк не міг її знову зібрати у квадратну форму.Він намагався це зробити багато днів поспіль, намалював численні зразки та зображення. Наприкінці учень зрозумів: немає сенсу подорожувати в світ, бо легко можна знайти всю красу і різноманітність світу у семи шматках розбитої дощечки.

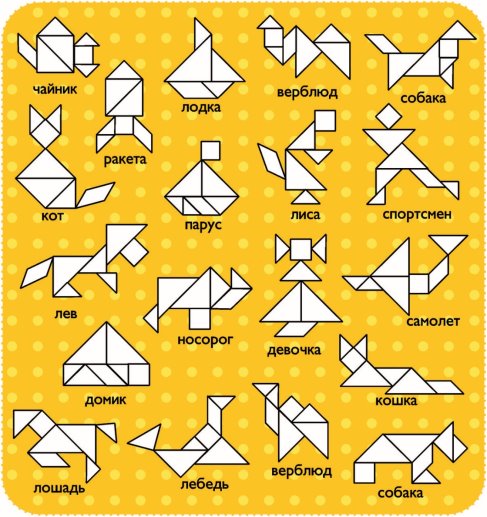
Влучний погляд

Висновок:
Використання різних методик розвиває логічне та критичне мислення, просторову уяву,   абстрактне мислення ,творчий підхід до справи.

                                   Усний рахунок

1. Множення і ділення на 4 (або 8).

Помножити на 4 (або 8) — означає двічі (або тричі) подвоїти число. Приклади: 26 ∙ 4 = 52 ∙ 2= 104; 126 ∙ 4 = 252 ∙ 2 = 504. Розділити на 4 (або 8) означає послідовно 2 (або 3) рази поділити дане число на 2.

2. Множення числа на 5.

5 – це половина 10, тому спочатку потрібно число поділити на 2 (якщо воно парне) і дописати 0, або навпаки, якщо непарне – дописати 0, а потім розділити на 2. 46 ∙ 5 = 46 : 2 = 23 ∙ 10 = 230; 67 ∙ 5 = 67 ∙ 10 : 2 = 335. Щоб розділити число на 5, виконуються аналогічні дії у зворотному порядку. 46 : 5 = 4,6 ∙ 2 = 9,2; 320 : 5 = 32 ∙ 2 = 64 або навпаки 46 : 5 = 92 : 10 = 9,2; 320 : 5 = 640 : 10 = 64. Такі обчислення можна виконувати після вивчення десяткових дробів.

3. Множення на 9, 99, 999.

До першого множника дописують стільки нулів, скільки дев'яток у другому множнику, і від результату віднімають перший множник. Приклади: 1)337 ∙ 9 = 3370 –337 = 3033. 2)42 ∙ 99 = 4200 – 42 = 4158. 3) 18 ∙ 999 = 18 000 – 18 = 17 982.

4. Множення чисел на 11.

Записують останню цифру числа (цифру з розряду одиниць), потім послідовно справа наліво записують суми двох сусідніх цифр числа, нарешті першу цифру числа. Приклади: 11 1)54 ∙ 11=594. а) Пишемо 4; б) 5 + 4 = 9, пишемо 9; в) пишемо 5. 2) 124 ∙ 11 = 1364. Записуємо справа наліво: 4; 6 = 2 + 4; 3 = 1 + 2; 1. 3)236 ∙ 11 = 2596. Записуємо справа наліво: 6; 9 = 3 + 6; 5 = 2 + 3; 2. Якщо одна із сум сусідніх цифр виявиться більшою від 9, то на відповідному місці записують цифру одиниць знайденої суми, а до наступної суми додають 1. Додають одиницю і до останньої цифри множника, якщо попередня сума перевищувала 9. Приклади: 1) 68 ∙ 11 = 748. а) Пишемо 8; б) 6 + 8 = 14, пишемо 4, пам'ятаємо 1; в) 6 + 1 = 7, пишемо 7. 2) 4769 ∙ 11 = 52459. а) Пишемо 9; б) 9 + 6 = 15, пишемо 5, пам'ятаємо 1; в) (6 + 7) + 1 = 14, пишемо 4, пам'ятаємо 1; г) (4 + 7) + 1 = 12, пишемо 2, пам'ятаємо 1; д) 4 + 1 = 5, пишемо 5.

 

5.Розподільний закон множення. (а + в) ∙ с = ас + bс, (а – в) · с = ас – bс.

Приклади: 1) 41 ∙ 8 = (40 + 1) ∙ 8 = 320 + 8 = 328; 2) 74 ∙ 9 = (70 + 4) ∙ 9 = 630 + 36 = 666; 3) 49 ∙ 4 = (50 – 1) ∙ 4 = 200 – 4 = 196; 4) 198 ∙ 4 = (200 – 2) ∙ 4 = 800 – 8 = 792; 5) 202 ∙ 3 = (200 + 2) ∙ 3 = 600 + 6 = 606; 6) 397 ∙ 5 = (400 – 3) ∙ 5 = 2000 – 15 = 1985.

6. Квадрати чисел, що закінчуються цифрою 5.

Квадрат двоцифрового числа а5 є числом, що дорівнює а(а + 1)∙100 +5 ∙ 5 Квадрат трицифрового числа ав5 обчислюється так: ав ∙ ( ав + 1)∙100 +25 Приклади: 1) 752 = 7 ∙ 8 ∙ 100 + 25 = 5625; 2) 952 = 9 ∙ 10 ∙ 100 + 25 = 9025; 3) 1152 = 11 ∙ 12 ∙ 100 + 25 = 13 225; 4) 2452 = 24 ∙ 25 ∙ 100 + 25 = 60 025.

Висновок:

Використовуючи усні вправи учні здобувають обчислювальні навички, закріплюють теоретичні знання, тренують увагу і пам’ять. Вдало підібрана система вправ сприяє розвитку логічного  мислення, привчає до уважності, формує вміння планувати свою діяльність.

               Розв’язування вправ (задач різними способами )

1.Логічні задачі:

 

1. Запиши, використовуючи три п'ятірки та знаки дій, числа 2; 0; 5.

           (5-5)*5=0 (5+5):5=2 5:5*5=5

2.Математичний софізм:

            5=3

Маємо очевидну рівність

            25-15-10=15-9-6

            5(5-3-2)=3(5-3-2)

             5=3

 2. Рішення задач різними способами.

 

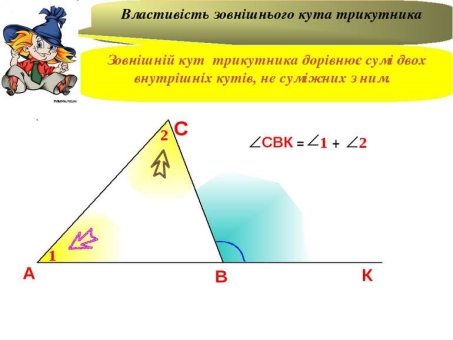
Кут СВК дорівнює 110 градусів, кут 2 дорівнює 80 градусів,знайти невідомі кути трикутни ка.

3. Правильно організований спосіб аналізу задачі - з питання чи від даних до питання.

Задача . Автомобіль використав за 4 год роботи 36 л бензину. Скільки літрів бензину потрібно для автомобіля на 8 годин роботи при тій самій нормі витрати за годину?

Норма витрати бензину	Час роботи	Загальна витрата бензину
однакова	4 год 8 год	36 л ?

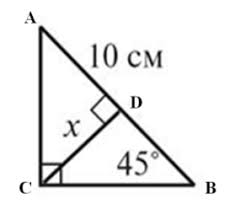
4. Уявлення ситуації, описаної в задачі (намалювати "картинку").

Учитель звертає увагу дітей на деталі, які потрібно обов'язково представити, а які можна опустити. Уявна участь у цій ситуації. Розбивка тексту задачі на значеннєві частини. Моделювання ситуації за допомогою креслення, малюнка.

 

 

 

 

 

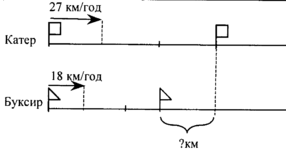
5. Самостійне складання задач учнями.

 

{\displaystyle \angle 4}

Висновок:

Рішення задач різними спсобами розвиває логічне та критичне мислення.Звичка знаходження іншого способу зіграє велику роль у майбутньому,але є доступною не всім учням, а лише тим , хто любить математику і має особливі математичні можливості.

Інтелектуальний математичний диктант.

• Кількість розрядів у кожному класі помножити на кількість см у метрі.
• Найменше двоцифрове число, складене з однакових цифр, помножене на кількість кг у центнері.
• Від кількості днів у невисокосному році відніміть кількість місяців року.
• Знайдіть добуток усіх цифр.
• Обчислити суму найменшого трицифрового числа і найбільшого двоцифрового.
• Кількість областей України помножити на кількість сторін квадрата.
• До числа міжнародного жіночого дня додайте число голосних букв у назві столиці України.
• До порядкового номеру ноти «ля» додайте кількість годин у добі.
• 3 дати останнього дня лютого у високосному році відніміть кількість пальців на одній руці.
• Кількість пір року помножити на кількість літніх місяців та відніміть кількість днів тижня.
• Кількість станів води поділіть на порядковий номер букви «в»
• Від кількості кольорів веселки відніміть кількість складів у слові шоколад.

Висновок:

Рішення задач різними спсобами розвиває логічне та критичне мислення.Звичка знаходження іншого способу зіграє велику роль у майбутньому,але є доступною не всім учням, а лише тим , хто любить математику і має особливі математичні можливості.

-ОТЖЕ,-сказав мудрець-МАТЕМАТИКА –це здивування, а через здивування пізнається світ.

 

Дякую за увагу!