Майстер-клас "Використання техніки орігамі для вивчення теми "Квадрат" в курсі геометрії 8 клас"

Незвичайне у звичайному

Доброго дня, шановні колеги. Запрошую вас поринути у світ незвичайної математики. І насамперед, замисліться будь-ласка над ось такими словами:

• Вдивляйтеся у звичайне і ви побачите неочікуване;
• Вдивляйтеся у некрасиве і ви побачите прекрасне;
• Вдивляйтеся в просте і ви побачите складне;
• Вдивляйтеся в маленьке і ви побачите величне.

До чого закликає нас японська мудрість? (роздуми)

Скажіть а чи любите ви математику? А чому ні? Можливо вам здається, що це дуже складна наука? На превеликий жаль так думає багато людей. Чомусь загальноприйнято вважати, що математика потрібна лише в магазині чи банку. Сьогодні я хочу спробувати переконати вас, що математика – це наше життя, а життя – це математика.

Вправа з чотирикутниками

У кожної групи набір фігур. Спочатку пропонується вибрати чотирикутники. Далі чотирикутники із прямими кутами. Хто знає як називаються такі чотирикутники? (прямокутники) Серед них виберіть ті, у яких всі сторони рівні. Скажіть з якою фігурою ми сьогодні будемо працювати? (квадрат)

Отже, тема нашого уроку: «Квадрат».

Відомий китайський філософ і мудрець Лао Цзи сказав, що: «Великий квадрат не має кутів.» Як ви думаєте, що він мав на увазі? Справа в тому, що в стародавньому Китаї квадрат виділяли серед інших геометричних фігур, більше того, його асоціювали із Землею, як символ Землі, який пересікається із космосом і уособлює нескінченний всесвіт. Саме напрямком, в якому основою є квадрат, ми і будемо сьогодні рухатися.

Візьміть в руки квадрат і роздивіться його. Що ви можете про нього сказати? (має чотири вершини, чотири кути, чотири сторони, всі сторони рівні, всі кути рівні і прямі,) Є сторони, які мають спільну вершину, вони називаються сусідніми, а ті які не мають спільних точок – протилежними.

Орігамі… Чи всім знайома така техніка? Так, отже, орігамі та математика, які гіпотези у вас викликає це словосполучення? (роздуми) Дійсно орігамі тісно пов’язане із математикою і дає хорошу основу для її вивчення. Усі деталі орігамі виготовляються із геометричних фігур і це найперше, що пов’язує цю техніку із математикою. Але якщо в математиці для того, щоб отримати ту чи іншу фігуру потрібні олівець і лінійка, то в орігамі, достатньо просто зігнути аркуш.

Вправа «Отримай правильний чотирикутник»

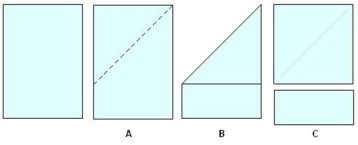
Візьміть в руки аркуш прямокутної форми. Зігніть дві сторони одна до одної, зайвий фрагмент відріжте ножицями. Розгорніть аркуш. Яку фігуру ви отримала? (квадрат) Отже, квадрат – це правильний чотирикутник.

Вправа «Склади свою фігуру з квадрата»

Візьміть в руки квадрат з двох боків різного кольору. А тепер загинаючи тільки одну сторону утворіть фігури лише з одного кольору. Які це будуть фігури? (трикутник, чотирикутник, п’ятикутник) Чому не можна утворити шестикутник? (роздуми) На прикладі цієї задачі можна довести, використовуючи за основу трикутник, п’ятикутник, що з довільного n-кутника можна утворити (n-1) кутні фігури.

Вправа «Ділення прямого кута на два та три рівні кути»

Візьміть в руки квадратний аркуш. Зігніть його (по діагоналі). Лінія згину – це лінія. На перетині таких ліній є точка. Як називається для квадрата така лінія? (діагональ) Скажіть, чи можете ви розділити прямий кут навпіл? Так, за допомогою транспортира або циркуля та лінійки. Подивіться на свій аркуш, ви щойно зробили це не використовуючи жодних додаткових інструментів. Діагональ – є бісектрисою квадрата. А чи можете ви поділити кут на три рівних частини? Зараз я спробую вас навчити. Для цього нам потрібно знайти середину сторони (зігніть аркуш по середині сторони). Лінія, яку ми отримали називається серединним перпендикуляром. Далі нижній правий кут загніть до серединного перпендикуляра.

 Вправа (Доведення теореми про суму кутів трикутника)

Візьміть квадрат і зігніть його по діагоналі. Яка фігура утворилася? (трикутник) А хто пам’ятає теорему про суму кутів трикутника? Зараз ми наочно доведемо з вами цю теорему. Для цього загніть протилежну вершину кута до діагоналі. Аналогічно загніть решта дві вершини.

І так всі три кути трикутника утворили собою лінію, тобто розгорнутий кут. А градусна міра розгорнутого кута 180⁰. Теорема доведена.

Давайте повернемося до нашого квадрата. Розгорнемо трикутник. Зі скількох трикутників складається квадрат? (з двох). Тоді чому дорівнює сума кутів квадрата? (360⁰). А чи тільки квадрат складається із двох трикутників? Ні. Ось наприклад довільний чотирикутник, поділений на два квадрати. А тепер сформулюйте узагальнену теорему про суму кутів будь-якого чотирикутника. (сума кутів будь-якого чотирикутника дорівнює 360⁰)

Візьміть квадрат і покладіть його на стіл. Фігура зайняла на столі певну площу – площу квадрата. Усі ми добре знаємо, що площу квадрата можна знайти множенням сторони на сторону. А як ви думаєте чи є інші формули для обчислення площі квадрата? Зараз ми з вами виведемо одну з таких формул, де відомі діагоналі квадрата.

Вправа «Площа квадрата»

Візьміть в руки квадрат і згорніть його по діагоналі. Тепер розгорніть і згорніть по іншій діагоналі. Всередині квадрата ми отримали точку перетину діагоналей. Тепер загорніть до неї усі вершини квадрата. Ми отримали два нових квадрата зі стороною, яка дорівнює половині діагоналі початкового. Отже, формула площі буде   S_кв

На сьогоднішньому уроці ми з вами познайомилися із маленькою плоскою фігурою – квадратом. Пригадали уже відомі факти та дізналися нові властивості цієї фігури. А ще зрозуміли, що уважно придивившись до маленького квадрата, можна побачити можливість для втілення будь-якої творчої фантазії.

Сьогодні ми з вами говорили про Східні традиції, мистецтво і звичайно ж квадрат. Одним із захопливих звичаїв на сході та й у нашому краї теж, є створення оберегів на щастя. Давайте зробимо зараз такий талісман удачі.

Вправа «Талісман удачі»

Візьміть квадрат і зігніть його по діагоналі. Далі правий та лівий кут загніть до діагоналі.

Хто спостережливий, помітить, що на даному етапі ми з вами поділили прямий кут на чотири рівні частини не використовуючи додаткових приладів. Далі ті кінці, що лишилися теж загинаємо до діагоналі. Далі за схемою. В результаті ми отримаємо модулі, які потрібно з’єднати між собою, нам знадобиться 8 модулів. По черзі з’єднайте свої модулі. Ми отримали талісман нашого заняття.

(подарувати кожному на згадку по талісману)

Шановні колеги, скажіть будь ласка чим ви займалися на уроці? (складали фігури, орігамі) А ви займалися математикою? Так, звичайно. Як ви вважаєте, яку користь приносить орігамі? (розвиває дрібну моторику, фантазію, полегшує сприйняття математичних теорем та аксіом, розвиває просторову уяву, наполегливість). (демонстрація на слайді)

 Ми працювали на уроці з квадратом, а це фігура плоска, а з неї ми отримували об’ємні просторові фігури. Отже, орігамі дозволяє поєднувати такі дві частини математики, як планіметрія (вивчення фігур на площині) та стереометрія (вивчення фігур у просторі).

Пригадайте слова Лао Цзи, які звучали на початку уроку. Чи дійсно ми з вами довели, що квадрат – це фігура без кутів? Так, адже зі звичайного квадрата можна отримати незвичайні модулі і квадрат – це дійсно фігура, яка є початком для творення чогось прекрасного і величного.

(демонстрація на слайдах варіанти орігамі)

А де ще можна використовувати орігамі? (на уроках технологій, георфії, біології, природознавства) Крім цього у нас в усіх є діти, внуки, тому фантазуйте, експерементуйте, творіть. І пам’ятайте, що ви завжди займаєтеся математикою! Адже математика – це наше життя, а життя – це і є математика. Дякую усім за співпрацю!

Для підготовки уроку використала матеріали  учителя математики МАОУ Чигиринської ЗОШ Ванюхіної Н.С. та посібник «Математика та паперопластика», Киба С.В.