Конспект уроку з геометрії для 8 класу на тему:"Чотирикутники"

Тема. Чотирикутники

Мета: узагальнити основні теоретичні знання про паралелограм, прямокутник, ромб, квадрат, трапецію, звернути увагу учнів на зв'язок між цими фігурами; підготувати учнів до контрольної роботи шляхом розв'язування задач різного рівня; активізувати роботу учнів відпрацьовувати вміння робити логічні висновки; формувати навички дослідницької роботи; виховувати критичне ставлення до своєї роботи, а також вміння оцінювати свої знання,

Тип уроку: узагальнення й систематизація знань

 Очікувані результати: Після уроку учні зможуть:

• повторити основний теоретичний матеріал про паралелограм, ромб, прямокутник, квадрат, трапецію;

• удосконалити свої вміння й навички розв'язування задач з теми «Чотирикутники»;

• робити логічні висновки, аналізувати вивчений матеріал;

• поглибити вміння оцінювати свої знання

Хід уроку

I. Організаційний момент

Учитель. Сьогодні в нас незвичайний урок. Я відкриваю приватне детективне агентство й набираю співробітників. В агентстві будуть працювати математично грамотні співробітники, що вмі­ють логічно мислити й приймати швидкі рішення. Одним із них можете стати й ви, якщо успішно пройдете стажування. Я прошу вас об'єднатися в п'ять слідчих груп. Кожна група має обрати начальника підрозділу.

Сьогодні я пропоную вам узяти участь у пошуку п'ятьох підозрюваних. На основі результатів пошуку я зроблю висновки про професійну придатність кожного з вас.

II. Установлення осіб підозрюваних і складання їхніх портретів

(актуалізація опорних знань учнів)

Завдання для І слідчої групи

У підозрюваного № 1 лише дві протилежні сторони паралельні. (Відповідь: трапеція.)

Завдання для II слідчої групи

У підозрюваного № 2 протилежні сторони паралельні. (Відповідь: паралелограм.)

Завдання для III слідчої групи

У підозрюваного № 3 протилежні сторони паралельні й усі кути прямі. (Відповідь: прямокутник.) Завдання для IV слідчої групи

У підозрюваного № 4 протилежні сторони паралельні й дорівнюють одна одній. (Відповідь: ромб.) Завдання для V слідчої групи

У підозрюваного № 5 протилежні сторони паралельні, усі його кути прямі, а всі сторони однакові. (Відповідь: квадрат.)

Увага! Група має на обмірковування 1 хвилину. Після цього начальник слідчої групи має встановити особу підозрюваного.

Тепер у кожної слідчої групи є ще З хвилини на обговорення й складання портрету підозрюваного. (Кожна група згадує властивості «свого» чотирикутника, на підставі чого й складає його портрет.)

Можливі відповіді

I слідча група. Якщо в трапеції дві бокові сторони рівні, то вона називається рівнобічною. У рівнобічної трапеції ріпні діагоналі й кути при основі. Відрізок, який сполучує середини бічних сторін, називається середньою лінією трапеції. Середня лінія трапеції паралельна основам і дорівнює їх півсумі.

II слідча група. У паралелограма діагоналі перетинаються й діляться точкою перетину навпіл. Протилежні сторони рівні. Протилежні кути паралелограма так само рівні. Кути, що прилягають до однієї сторони паралелограма, складають у сумі 180". Діагональ паралелограма поділяє його на два рівних трикутники.

III слідча група. Діагоналі прямокутника перетинаються й діляться точкою перетину навпіл. Діагоналі прямокутника рівні. Протилежні сторони прямокутника рівні.

IV слідча група. Діагоналі ромба перетинаються й діляться точкою перетину навпіл. Діагоналі ромба є бісектрисами його кутів. Діагоналі ромба перетинаються під прямим кутом. Протилежні кути ромба рівні. Сума кутів, що прилягають до однієї сторони ромба, становить 180°.

V слідча група. Діагоналі квадрата перетинаються й діляться точкою перетину навпіл. Діагоналі квадрата рівні. Діагоналі квадрата є бісектрисами його кутів. Діагоналі квадрата перетинаються під прямим кутом.

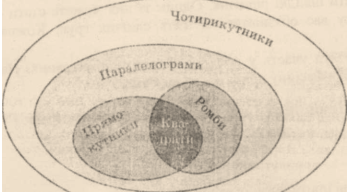
Учитель. Вислухавши ваші доповіді з описом портретів, ми встановлюємо взаємозв'язок між підозрюваними, який відображено на цьому рисунку.

III. Слідчий експеримент (розв'язування задач)

Учитель. Наші підозрювані мають одну небезпечну властивість. Вони вміють перевтілюватися ви повинні навчитися розпізнавати їх за будь-яких обставин. Отримайте завдання.

Завдання для слідчих груп

І слідча група. Доведіть, що коли в паралелограмі всі кути рівні, то він є прямокутником.

Оскільки дана фігура — паралелограм, то сума кутів, що прилягають до однієї з його сторін, становить 180°. За умовою всі кути рівні. Таким чином, два кути, що прилягають до однієї сторони паралелограма, будуть мати по 90°, а оскільки протилежні кути в паралелограмі рівні, то й два інших кути будуть мати по 90°. Отже, дана фігура за визначенням — прямокутник.

// слідча група. Доведіть, що коли в паралелограмі хоча б один кут прямий, то він — прямокутник.

Оскільки в паралелограмі сума кутів, що прилягають до однієї сторони, становить 180°, а за умовою один із них дорівнює 90°, то й другий так само дорівнює 90°. А оскільки протилежні кути паралелограма рівні, то всі кути в даному паралелограмі прямі. Отже, в цього паралелограма всі кути прямі й він є прямокутником за визначенням.

 

 

 

 

 Iслідча група. Доведіть, що коли в паралелограмі діагоналі рівні, то він є прямокутником.

Доведення _г,

Нехай ABCD— паралелограм (рис. І).         А                                                             В

 

 

                                                                                                                                              D                                                 С

                                                                                

За властивостями протилежних сторін паралелограма AD -=ВС. За умовою АС = DB і сторона АВ — спільна в трикутнику DAB і СВА. Отже, ∆DВA=∆С В А за трьома сторонами.

Звідси <DAB = < СВА Оскільки <DAB + <СВА = 180°, то

 

 

 

 

<DAB=< СВА =180°:2 = 90°. Оскільки <A = <C, а <В = <   D (властивість протилежних кутів паралелограма), то <A = <C=<B =<D = 90° . Таким чином, паралелограм ABCD є прямокутником.

Примітка. Слід звернути увагу учнів на те, що, вислухавши доповідь II групи, цю ознаку можна було довести коротше.

Wслідча група. Доведіть, що чотирикутник, у якого всі сторони рівні є ромбом.

Доведення:

Розглянемо чотирикутник АВСВ (рис. 2). За умовою АВ = ВС = C СВА = A DAB. Проведемо діагональ BD. Отримаємо ABAD = ADCB за трьома сторонами. Звідси LCBD = LADB, але вони внутрішні перехресні при прямих ВС і A D та січній BD. Отже, ВС \ \ АВ . Аналогічно, AABD = L СОВ , а вони внутрішні перехресні при прямих АВ і CD і січній BD. Отже, АВ \\ CD . Звідси випливає: ABCD — паралелограм, у якого всі сторони рівні.

Таким чином, ABCD — ромб, що й потрібно було довести.

 

                        В                                                             В                           С

       

         А                            С

 

                                                                                               

Рис. 2                D                                              А                      D   рис 3                 

V слідча група. Доведіть, що коли діагоналі прямокутника перетинаються під прямим кутом, то він є квадратом.

Доведення:

Нехай ABCD — прямокутник (рис. 3). AC.┴BD за умовою, АС = BD (властивість діагоналей прямокутника), АО = СО = ВО = OD (властивість діагоналей прямокутника). Звідси випливає рівність прямокутних трикутників: ∆АОВ = ∆ВОС = ∆СОВ = ∆AOD. Отже, АВ = ВС = CD = AD . Тобто ABCD — прямокутник, у якого всі сторони рівні.

Таким чином, ABCD — квадрат, що й слід було довести.

 

 

Учитель.  Отже, слідчий експеримент ми закінчили й висунули звинувачення чотирьом підозрюваним. Проте п'ятого ми так і не зловили. Нам відоме тільки його ім'я — трапеція!

IV. Проведення експертизи речових доказів

(розв'язування опорних задач за готовими рисунками

 

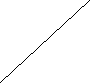
1. За рис. 4 доведіть, що < АОВ = 90°,

Доведення:

Оскільки ВС II AD і АВ — січна, то <A +<B = 180° як внутрішні однобічні. Отже, сума половин цих дорівнює 90°. Отже, у трикутнику АОВ <АОВ = 180° - 90° = 90°, потрібно було довести.

2. За рис. 5 доведіть, що BC=BF. Доведення:

ВС II AD як основи трапеції. Отже, <BCE =<FDE як внутрішні перехресні при паралельних прямих ВС і AF та січній CD.  <ВЕС=< FED як вертикальні, СЕ = ED за умовою. Таким чином, ∆BC Е  =∆ FED за стороною й двома прилеглими до неї кутами. Звідси ВС = BF.

3. За рис. 6 доведіть, що АВ = СВ.

 Доведення:

Трикутник AOD — рівнобедрений з основою AD (за умовою AО=.О D

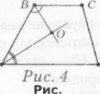
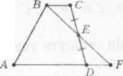                             рис5

 

 

Звідси за властивістю кутів рівнобедреного трикутника < ОА D=<ODA. Отже,  <CBO =  <.ВСО, оскільки з паралельності ВС іAD випливає, що <OAD = < BCO, <ODA = <CBO.

Таким чином, трикутник ВОС — рівнобедрений з основою ВС.' Звідси  В О = ОС

. Розглянемо трикутники BOA і COD.

<COD =<BOA як вертикальні, ВО = СО згідно з вище доведеним. АО = OD за умовою. Отже. ∆ВОА = ∆COD за двома сторонами й кутом між ними. Звідси АВ =CD, що й треба було довести.

 

                                   В               С                                                                    В                          С

 

 

 

    

               Рис 6                                       D                                             А                               

            А                                                                                                                    Е                     D

                                                                                                    рис7                                         

  4. За рис. 7 знайдіть кути трапеції, якщо BE \ \ CD <А=40, <АВЕ=75    

Розв язання:

Із трикутника АВ Е  <Е= 180°-(40° + 75°) = 65°.

Оскільки ВЕ\ \ЕВ, ВС і AD — основи трапеції і ВЕ — січна, то < СВЕ = < BEA=

= 65°.

Таким чином, < ABC = < ABE + < СВЕ = 75° + 65° = 140°. Оскільки BC\\DE і BE\\CD. то BCDE— паралелограм. Звідси <D = <СВЕ = 65°, a < С = 180°-65°= 115°. Отже, <A =40°, <B = 140°, <.C = 115°, <B = 65°.

        

5. За рис. 8 знайдіть кути трапеції, якщо <С- <А = 40°

. Розв'язання:

Оскільки АВС D— рівнобічна трапеція {А В = СО), то <А Тоді <С-< D= 40°, а <С + < D=180°. Звідси 2 <С = 220°, < С = 110°, < D= 70°.

Отже,       <А= < D= 70°, <В =<С = 110°.

Відповідь: 70°, 110°, 110°, 70°.

Учитель. Доки слідчі п'ятьох груп опрацьовують речові докази, найкращі професіонали, по одному з кожної групи, працюватимуть над задачею з висунення звинувачення злісній правопорушниці.

V. Висунення звинувачення (розв'язування творчої задачі) За рис. 9 знайдіть периметр трапеції, якщо А D= 15 .                        С

А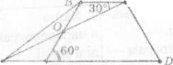 

                    Е         Рис. 9

Розв язання:

ВС\\АВ (ВС і AD — основи трапеції), BC\\DE, СЕ — січна. Звідси <BCO = <AEO = 30° як внутрішні перехресні. Розглянемо трикутник CDE.

<ECD = 90° за умовою. Звідси <CDE = 90°-30³ = 60°. Отже, у трапеції ABCD <D = <A. Таким чином, ABCD — рівнобічна трапеція, АВ = CD. Розглянемо трикутники ВСО і АЕО. ВО = АО за умовою, <ВОС = < ЕОА як вертикальні, < ОВС = <OAF як внутрішні перехресні при ВС\ \D Е й січній А В. Звідси ∆ВСО = ∆АЕО за стороною й двома прилеглими до неї кутами. Звідси АЕ = ВС = 5 . Отже, DE = AD + АЕ= 15 + 5 = 20 .Із прямокутного трикутника DCE     ( <С = 90°) отримуємо CD = 10 (лежить навпроти кута 30°). АВ = CD = 10. Pabcd= АВ+ BC+CD+AD=210+5+15=40. Відповідь: 40.

VI. Підбиття підсумків роботи слідчих груп

Учитель. Як директор детективного агентства маю сказати, що слідчі групи продемонстрували належний професіоналізм і можуть бути зараховані до штату агентства. За

відмінну роботу висловлюю подяку із відзнакою в журналі таким стажистам... (називає прізвища учнів, які активно працювали на уроці).

Роботу решти членів слідчих груп пропоную оцінити самостійно й подати списки від кожної групи.II.      Домашнє завдання

Скласти звітну таблицю (опорний конспект) із теми «Чотирикутники».

Один із варіантів опорного конспекту

Чотирикутник

А ВС В — чотирикутник. АіС,В iD — протилежні вершини.

АВ і С D, А D і ВС — протилежні сторони.

А і В, В і С, АВ і ВС, СІ) і АО — сусідні вершини й сторони.

Поодинокі випадки чотирикутників

Паралелограм | Прямокутник     Ромб               Квадрат

 

Властивості паралелограма	Властивості прямокутника	Властивості ромба	Властивості квадрата
1. Діагоналі в точці перетину діляться навпіл. 2. Кожна діагональ ділить паралелограм на два рівних трикутники. 3. Протилежні сторони рівні, й протилежні кути рівні.	1. Усі властивості паралелограма. 2. Усі кути прямі. 3. Діагоналі  рівні,	1. Усі властивості паралелограма. 2. Діагоналі ромба перетинаються під прямим кутом і є бісектрисами його кутів	1. Усі кути прямі. 2. Діагоналі квадрата рівні, перпендикулярні і є бісектрисами

 

. Ознаки

Паралелограм    Прямокутник                Ромб             Квадрат

 

1. Якщо діагоналі чотирикутника попарно перетинаються й діляться в точці перетину навпіл, то цей чотирикутник є паралелограмом. 2. Якщо протилежні сторони чотирикутника рівні, то цей чотирикутник- паралелограм. 3. Якщо дві сторони чотирикутника рівні й паралельні, то цей чотирикутник — паралелограм

Якщо в паралелограма діагоналі рівні, то цей паралелограм — прямокутник.

1. Якщо в паралелограма діагоналі перпендикулярні, то цей паралелограм є ромбом. 2. Якщо в паралелограма діагоналі є бісектрисами його кутів, то цей   паралелограм — |ромб

Якщо в прямокутника діагоналі перетинаються шд прямим кутом, то цей прямокутник квадрат

 

Трапеція      

                   ВС\ \ А D;  АВ\ \  С D

                                     

ЕF =(А D-ВС)⁄2

А1 В1—средня лінія

А1 В1\ \ВС 

 

А1 В1 =( ВС+ А D)⁄2