Метод координат дляматеріал до уроку "Знаходження геометричного місця точок. Задача одна, а розв’язків декілька."

Про матеріал

Матеріал для уроку "Метод координат для знаходження геометричного місця точок.Задача одна, а розв'язків декілька" дає можливість розглянути розв'язання геометричних задач декількома способами.

Перегляд файлу

Метод координат для знаходження геометричного місця точок.

Задача одна, а розв’язків декілька.

Розв’язування задач на відшукання ГМТ за допомогою методу координат передбачає два етапи:

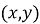
скласти рівняння з двома невідомими , яке задовольняють координати будь-якої точки шуканого ГМТ.
довести обернене твердження: будь-яка точка, координати якої задовольняють знайдене рівняння, належить шуканому ГМТ.

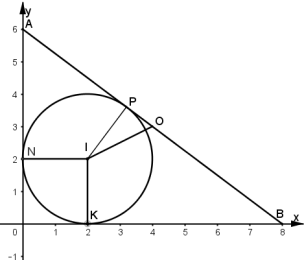
Задача . В прямокутному трикутнику з катетами 6см та 8см знайти відстань між центром вписаного кола та центром описаного навколо нього кола.

Перший спосіб. Розв’язання.

В прямокутному трикутнику з катетами см вибираємо систему

Другий спосіб. Розв’язання.

В прямокутному трикутнику з катетами 6см та 8см гіпотенуза дорівнює 10см, радіус вписаного кола

==2(см), радіус описаного кола 5см.За властивістю дотичних, проведених з однієї точки маємо см, 6см, =4см, 5см, 1см, прямокутний. ∆, ∠, відстань між центром вписаного кола та центром описаного навколо нього кола.

= =(см).

координат так, щоб початок координат знаходився у вершині прямого кута, а інші на осях координат. . Центр описаного кола точка є серединою . Радіус вписаного кола ==2(см), −центр вписаного кола. відстань між центром вписаного кола та центром описаного навколо нього кола знайдемо за формулою відстані між точками

=(см).

Відповідь.см.

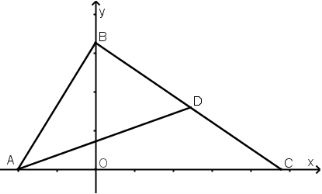
Задача . В трикутнику ∆ знайти медіану, проведену з вершини якщо , ∠∆

Перший спосіб. Розв’язання.

Виберемо систему координат так, щоб вісь співпадала б з стороною ∠∆ тоді в ∆ ∠∠, тоді .

Тепер встановлюємо координати вершин трикутника , . −медіана. Тому −середина , . За формулою відстані між двома точками за їх координатами, маємо

отже

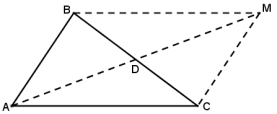
Другий спосіб. Розв’язання.

За теоремою косинусів маємо

+2⋅cos∠

16+36-2⋅4⋅6⋅0,5=28,

Продовжимо медіану так, щоб Очевидно, що паралелограм. Скористаємось формулою зв’язку сторін та діагоналей паралелограма +, 28+=2⋅(16+36), після рівносильних перетворень одержимо , .