Методи розв'язування лінійних, квадратних рівнянь і нерівностей з параметрами

РОЗВ’ЯЗУВАННЯ ЛІНІЙНИХ І КВАДРАТНИХ РІВНЯНЬ І НЕРІВНОСТЕЙ З ПАРАМЕТРАМИ

 Поняття рівняння і нерівності з одною змінною і одним параметром, його розв’язок. Аналітичні способи розв’язування. Дослідження коренів квадратного рівняння (розв’язування нерівностей) відносно заданих точок.

Рівняння виду a · x = b, де a і b – дійсні числа (вираз який залежить від параметра), x – невідоме, називають лінійним рівнянням з одним параметром.

Коренем рівняння називають значення змінної x, при якому рівняння перетворюється у вірну числову рівність.

В залежності від значення параметра а та b рівняння має:

1. єдиний корінь x = , якщо а ≠ 0;
2. нескінченну множину коренів, якщо а = 0 і b = 0;
3. не має жодного кореня, якщо а = 0, b ≠ 0.

Це і є схема розв’язування лінійного рівняння з параметром.

Розв’язати рівняння з параметром означає знайти всі значення параметра при яких: 1) нема коренів, 2) є корені і знайти їх.

Завдання 1. Розв’язати рівняння

(a² – 6a + 5) · x = a – 1

Розв’язування. Запишемо рівняння у вигляді:

(a – 1) · (a – 5) · х = a – 1

Розглянемо слідуючі випадки:

1. якщо а = 1, то рівняння матиме вигляд 0 · х = 0. Коренем рівняння є любе дійсне число;
2. якщо а = 5, тоді рівняння запишемо у вигляді 0 · х = 4; рівняння немає коренів;
3. а ≠ 5, а ≠ 1, тоді, розділивши обидві частини рівняння на (а – 1), отримаємо рівняння (a – 5) · х = 1.

Звідси х = – єдиний корінь даного рівняння.

Відмітимо, що значення параметра як а = 1, а = 5 в розглянутому завданні називають контрольними значеннями параметра, оскільки в залежності від них рівняння міняє вигляд і відповідно міняються розв’язки рівняння.

До задач з параметрами які розглядаються в шкільному курсі математики, можна віднести, наприклад знаходження розв’язків лінійних і квадратних рівнянь в загальному вигляді, дослідження кількості їх в залежності від значення параметра.

При розв’язанні задач з параметрами слід запам’ятати головне: параметр являється фіксованим але невідомим числом і має подвійну природу:

1. пропонована відомість дозволяє «працювати» з параметром як з числом;
2. степінь дозволеності «роботи» з параметром обмежена його невідомістю.

Наприклад, ділення на вираз, який містить параметр добування кореня парного степеня із виразу з параметром потребує попередніх досліджень, оскільки результати їх впливають на розв’язок задачі.

Розглянемо декілька елементарних прикладів.

Завдання 2. Порівняти

• а і 3 а.

Розв’язування. Розглянемо слідуючі випадки:

1. якщо а = 0, – а = 3 а;
2. якщо a < 0, то – а > 3 a;
3. якщо a > 0, то – а < 3 a.

Завдання 3. Розв’язати рівняння а · х = 1.

Розв’язування. Контрольні значення параметру а = 0. Розглянемо слідуючі випадки:

1. якщо а = 0, то рівняння матиме вигляд 0· х = 1 і воно не має коренів;
2. якщо а ≠ 0, то х = – єдиний корінь рівняння.

Відповідь: при а = 0 нема коренів; при а ≠ 0 х = .

Завдання 4. Розв’язати рівняння (а² – 1) · х = а + 1.

Розв’язування. Приведем дане рівняння до вигляду

(а – 1) · (а + 1) · х = а + 1. Контрольні значення параметру а = 1 і а = - 1.

Розглянемо слідуючі випадки:

1. якщо а = 1, то рівняння матиме вигляд 0 · х = 2 і не матиме коренів;
2. якщо а = - 1, отримаємо з рівняння 0 · х = 0 і коренями є любе дійсне значення х;
3. якщо а ≠ 1 і а ≠ - 1, то 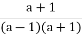х = , х = 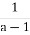– єдиний корінь.

Відповідь: якщо а = 1 – рівняння не має коренів; якщо а = - 1, то х Є R; якщо а ≠ 1 і а ≠ - 1, то х = .

Завдання 5. Розв’язати нерівність а · х < 1.

Розв’язування. Якщо а = 0, то рівність набере вигляду 0 · х < 1 і буде вірна для любого х з множини R.

Якщо а > 0, то х < (розділивши обидві частини нерівності на додатне число).

Якщо а < 0, то х > (розділивши обидві частини нерівності на від’ємне число).

Відповідь: а = 0, х Є R; а > 0, х Є (- ∞ ; ); а < 0, х Є ( + ∞).

Зверніть увагу, що при розв’язування даного завдання областю допустимих значень як для змінної так  і для параметру є множина всіх дійсних чисел.

Розглянемо завдання другого типу.

Завдання 6. Розв’язати рівняння   = 0.

Розв’язування. Дане рівняння рівносильне системі

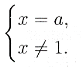
Звідси, якщо а ≠ 1, то розв’язком буде х = а; якщо а = 1, то розв’язків не буде.

Відповідь: якщо а ≠ 1, х = а; якщо а = 1, розв’язків немає.

Розглянемо завдання, де за рахунок параметру на змінну накладаються певні обмеження.

Для таких задач використовується формулювання: при яких значеннях параметра рівняння (нерівності, системи) має  єдиний (два, нескінченна множина) розв’язок (розв’язків)?; Знайти значення параметра, при якому розв’язок рівняння (нерівності системи) є деяка підмножина дійсних чисел.

Завдання 7. При яких значеннях параметра а нерівність

(х – а) · (х – 2) ≤ 0 має єдиний розв’язок?

Розв’язування. Очевидно, якщо а ≠ 2, то рішенням нерівності буде відрізок, а при а = 2 нерівність матиме вигляд (х – 2)² ≤ 0, матиме єдиний розв’язок х = 2.

Завдання 8. При яких значеннях параметру а рівняння ах² – х + 3 = 0 має єдиний корінь?

Розв’язування. а = 0 – контрольне значення параметру. Розглянемо два випадки:

1. а = 0, рівняння набере вигляду – х + 3 = 0, х = 3 єдиний корінь;
2. а ≠ 0, рівняння ах² – х + 3 = 0 – квадратне рівняння відносно змінної х і має єдиний корінь, якщо D = 0.

D = (- 1)² – 4 · а · 3 = 1 – 12а. Розв’язавши рівняння 1 – 12а = 0 маємо

а = .

Відповідь: при а = 0 і а = .

Завдання 9. При яких значеннях параметра а рівняння

а · (а + 3) · х² + (2а + 6) · х – 3а – 9 = 0 має більше одного кореня?

Розв’язування. Розглянемо слідуючі випадки враховуючи, що контрольні значення параметра а = 0 і а = - 3:

1. а = 0, рівняння матиме вигляд 6х – 9 = 0, отже х = – єдиний корінь;
2. а = - 3, рівняння матиме вигляд – 3 · (-3) – 9 = 0, рівність вірна, отже коренем рівняння є любе дійсне число;
3. а ≠ 0 і а ≠ - 3, розділивши обидві частини рівняння на (а + 3), отримаємо а · х² + 2х – 3 = 0.

Запишемо: D = 2² – 4 · а · - 3 = 4 + 12а > 0, а > - – при таких значеннях а рівняння матиме два кореня. Відмітимо, що а = 0 потрібно виключити з даного проміжку.

Відповідь: при а = - 3, якщо - < a < 0, якщо a > 0.

Завдання 10. Знайти всі значення параметра а, при яких тільки один  корінь квадратного тричлена х² – 2х (а + 1) + 6а – 3 більший 2.

Розв’язування. Знайдемо корені квадратного тричлена

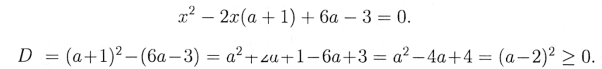
 Якщо D = 0, то а = 2. Отже х₁ = х₂ = 3 – рівняння має єдиний корінь і він більший 2.

Якщо D > 0, то рівняння має два різних корені х₁ = 3; х₂ = 2а – 1.

Оскільки х₁ > 2, то такою властивістю має володіти єдиний корінь і необхідно, щоб виконувалася умова, що х₂ ≤ 2, тобто 2а – 1 ≤ 2.

Звідси 2а ≤ 3, а ≤ .

Відповідь: при а = 2, а ≤ .