Урок алгебри у 8 класі. Тема. Формула коренів квадратного рівняння

Тема. Формула коренів квадратного рівняння

Мета:  ознайомити учнів з  формулами коренів квадратного рівняння; формувати вміння розв’язувати квадратні рівняння за алгоритмом; розвивати пам’ять та алгоритмічне мислення учнів; формувати вміння встановлювати логічні зв’язки; виховувати самостійність, впевненість у собі, культуру математичного мовлення учнів.

Тип уроку: засвоєння нових знань.

Хід уроку

I. Організаційний момент.

Відкриваємо зошити, записуємо число, класна робота.

ІІ. Перевірка домашнього завдання

Зібрати після уроку зошити і перевірити виконання домашнього завдання.

IІI. Актуалізація опорних знань

1. Фронтальне опитування:

• Сформулюйте означення квадратного рівняння. (прикріпити на дошці рівняння)
• Як називають коефіцієнти квадратного рівняння? а – перший коефіцієнт, b – другий, с – вільний член.
• Чому на коефіцієнт а накладається додаткова умова? Рівняння стає лінійним.
• А чи можуть другий коефіцієнт і вільний член дорівнювати нулю? Так.
• Як тоді називаються рівняння? Неповні.
• Записати на дошці види неповних квадратних рівнянь.
• Що таке зведене квадратне рівняння? а=1.
• Записати на дошці зведене квадратне рівняння.  

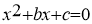
2. Вправа «Ланцюжок відповідей».

Завдання1: Назвати коефіцієнти квадратних рівнянь:

-2х²  + 3х - 4 = 0;

11-3х² +4=0;

12+ х² - 5х = 0;

7х -х² =5;

-х² -2х+5=0.

Завдання2: Скласти квадратне рівняння за даними коефіцієнтами:

 а=4,  b=-2,  с=3;

 а=2, b=-1,   с=0;

 b=7,  а=-1, с=4;

 b=0,  с=0,  а=-1;

 с=-5,  а=2,  b=-1.

IV. Мотивація навчальної діяльності.

1.                     Оголошення теми і мети уроку.

На попередніх уроках ви навчилися розв’язувати неповні квадратні рівняння, і зараз ми повторили все необхідне для того, щоб навчитися розв’язувати повні квадратні рівняння. Тому запишемо тему уроку: Формула коренів квадратного рівняння. (записую на дошці).

2.                     Історична довідка.

Квадратні рівняння простіших видів вавилонської матема­тики вміли розв'язувати ще 4 тис. років тому. Згодом розв'язували їх також: в Китаї і Греції.

Особливо багато у­ваги квадратним рівнянням приділяв Мухаммед аль-Хорезмі (IX ст.).

Він показав, як розв'язувати рівняння видів , але тільки при додатних а і b. Від'ємних коренів тоді не знаходили.

Формули коренів квадратного рівняння в тому вигляді, в якому ми їх вивчатимемо сьогодні на уроці, вперше вивів французький математик Франсуа Вієт. (XVIст.). Він першим почав позначати буквами не лише невідомі, а й коефіцієнти рівнянь.

Франсуа називав алгебру аналітичним мистецтвом. Він писав у листі до свого друга де Партене: «Всі математики знали, що під алгеброю приховані незрівнянні скарби але не вміли їх знайти...»

Сьогодні на уроці ми спробуємо знайти частинку цих скарбів.

V. Вивчення нового матеріалу.

1. Ознайомлення з формулами для обчислення коренів квадратного рівняння

Формули коренів квадратного рівняння можна отримати різними способами. Розглянемо один із них:

Помножимо обидві частини рівняння на 4а (а≠0) 

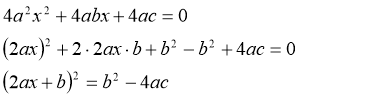
Позначимо  вираз b²-4ac через D:

D= b²-4ac.  (прикріпити на дошці)

Цей вираз називають дискримінантом квадратного рівняння. 

В перекладі з латинської мови це слово означає «розрізняти», «розділяти».

А в тлумачному математичному словнику записано: дискримінант квадратного тричлена - величина, що визначає характер його коренів.  

Тоді:

(2ax+b)²=D

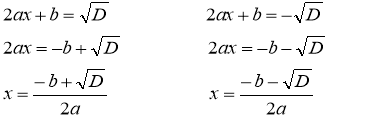
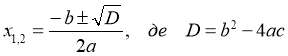
Проаналізуємо отриману формулу:

Якщо , то рівняння має 2 корені.

Якщо , то рівняння має 2 однакових  кореня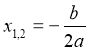

Якщо , то рівняння коренів не має.

Отже, від дискримінанта залежить кількість коренів квадратного рівняння.

В процесі викладення матеріалу на дошці утворилася схема:

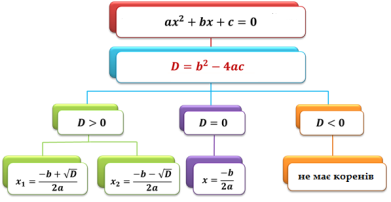
2.  Складання алгоритму розв’язування квадратного рівняння.

     (На основі схеми учні складають алгоритм розв’язання квадратного рівняння). Такі схеми роздати учням.

VІ. Первинне сприйняття нового матеріалу.

        Демонстраційний приклад ( розв’язує вчитель на дошці):

Зх²-2х-16=0

а=?  b=? с=?

D=(-2)²-43(-16)=4+192=1960

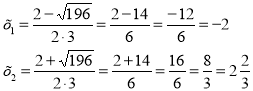
Відповідь: -2;

VІІ. Формування вмінь (робота з підручником)

Письмові вправи

Учні по черзі виконують біля дошки.

№ 927 №924 Знайти дискримінанти квадратних рівнянь.

№ 931 Користуючись формулою коренів, розв’яжіть рівняння.

№ 933 (а,б) – учні виконують в парах.

VІІІ. Підсумки уроку

Логічна вправа «Встановлення відповідності».

- На дошці малюнок світлофора.

Як ви думаєте, з яким поняттям, вивченим сьогодні на уроці він логічно взаємопов’язаний?

- Встановіть якому кольору відповідає яке значення дискримінанта.

( учні записують на червоному - D 0; на жовтому – D=0; на зеленому - D0)

 Рефлексія.

- Молодці. Ви добре сьогодні працювали. Дякую за урок. І бажаю, щоб у житті вам зажди горіло зелене світло!

IX. Домашнє завдання

Вивчити § 20

Виконати № 930

Встановити:

Чи залежить кількість коренів рівняння від знаку числа b? Чому?

Чи залежить кількість коренів рівняння від знаків чисел а і с? Як?

якщо а і с одного знаку, то рівняння може мати 2 однакові корені,  а може й не мати коренів;

якщо а і с різних знаків, то рівняння завжди матиме 2 різні корені

-2х² + 3х - 4 = 0;

11-3х² +4=0;

12+ х² - 5х = 0;

7х -х² =5;

-х² -2х+5=0.

а=4,  b=-2,  с=3;

а=2, b=-1,   с=0;

b=7,  а=-1, с=4;

b=0,  с=0,  а=-1;

с=-5,  а=2,  b=-1.

х²+aх=b

х²+a=bx

ах+b= х²