Методи розв’язування нерівностей з однією змінною

Алгебра

11 клас

(профільний рівень)

Тема. Методи розв’язування нерівностей з однією змінною: рівносильні перетворення, заміна змінних, застосування властивостей функцій, метод інтервалів (слайд 1).

Мета дидактична: узагальнити та систематизувати знання учнів з теми «Нерівності з однією змінною» ; формувати вміння  та навички застосовувати різні методи розв’язування нерівностей (рівносильні перетворення, заміна змінних, застосування властивостей функцій, метод інтервалів). (слайд 2)

 Мета виховна: виховувати  взаємоповагу, акуратність в записах, працьовитість, інтерес до математичних знань, виховувати уміння вислухати інших, виховувати активність, дисциплінованість, самостійність (самостійно працювати з|із| |посібндидактичними завданнями).

Корекційно-розвиваюча мета: розвивати пізнавальну діяльність, мовний розвиток , сенсоматорний розвиток (виконувати всі дії, необхідні в досягненні результату); розвивати зорово-слухову| пам'ять, увагу, логічне мислення (уміння лаконічно висловлювати свою математичну думку), розвивати уміння орієнтуватися в нестандартних ситуаціях,  навички роботи у групах, комунікативні і соціальні компетенції; розвивати навички раціонального використовування часу.

Тип уроку: комбінований

• систематизація знань;
• формування умінь, навичок.

Обладнання: роздатковий матеріал,  підручник

Орієнтований план і методи проведення уроку

1. Організаційний момент ( підготовка до уроку, емоційне налаштування)
2. Мотивація
3. Оголошення, представлення теми та очікувальних навчальних результатів
4. Методи розв’язування рівнянь з однією змінною: рівносильні перетворення, заміна змінних, застосування властивостей функцій, метод інтервалів (інтерактивна технологія « Ажурна пилка»)
5. Підведення підсумків, оцінювання результатів уроку

Хід уроку

І. Організаційний момент 

      Добрий день шановні учні! Ще 2400 років тому китайський педагог Конфуцій сказав:      

             „Те, що я чую , я забуваю.

               Те, що я бачу і чую, я трохи пам'ятаю.

               Те, що я чую, бачу і обговорюю, я починаю розуміти.

               Коли я чую, бачу, обговорюю й роблю, набуваю знань і навичок.”

        Тож закликаю вас до співпраці! (слайд 3).

ІІ.  Мотивація

На протязі декількох уроків ми приводили до системи свої знання по темі „Рівняння”. Оглянули основні відомості про рівняння (область визначення, розв'язок, рівносильність, втрата коренів та поява сторонніх коренів, перевірка розв'язків) та методи розв'язування рівнянь.

Сьогодні ми приступаємо до наступної, не менш цікавої, теми. Я сподіваюсь на успішну працю, що на уроці ми зможете показати свої знання, вміння, кмітливість, то ж будьте уважними, думайте, запитуйте, пропонуйте, оскільки нам разом з вами йти шляхом до  істини.

Я хочу,щоб на цьому уроці  ви показали наскільки ви компетентні в даній темі, тобто як ви володієте необхідною інформацією і вмієте застосувати набуті знання і досвід.

Сьогодні на уроці алгебри ми будемо  працювати разом і розраховувати на підтримку та допомогу один одного.

Кожному з вас хочу побажати,щоб на цьому уроці ви були  (слайд 4)

«У»- успішними

«С» - спокійними

«П» - прогресивними

«І» - ініціативними

«Х» - хоробрими

Підготуємо наші зошити до роботи. Пам’ятайте, що під час роботи з діловою документацією,її треба вести старанно, охайно, уважно ставитися  до цієї справи.                                                                             

ІІІ. Оголошення, представлення теми та очікуваних навчальних результатів  (запис дати та теми)                                                                                                                                   Дванадцяте березня                                                                                                                                                             Класна робота

Тема. Методи розв’язування нерівностей з однією змінною

Після цього уроку ви зможете:

(учні висловлюють думки, яких результатів вони досягнуть під час уроку)

ІV. Надання необхідної інформації

Вправа «Мікрофон»

Нерівністю зі змінною (невідомим) називають два вирази зі змінною (невідомим), між якими стоїть один із знаків нерівності:

                                           > (більше),

                                          < (менше),

                                          (більше або дорівнює; не менше),

                                          (менше або дорівнює; не більше).

Наприклад, 3х + 2 > 6,  х² + х +1 > 0 - нерівності.

Розв'язком нерівності називають значення змінної, яке перетворює його в правильну

числову нерівність.

Наприклад, число 2 - розв'язок нерівності х + 3 > 4.

Розв'язування нерівностей

Розв'язати нерівність з однією змінною означає знайти всі її розв'язки або довести, що розв'язків немає.

Нижче в таблиці наведено деякі числові підмножини, їх позначення, зображення на координатній прямій і запис у вигляді нерівності.

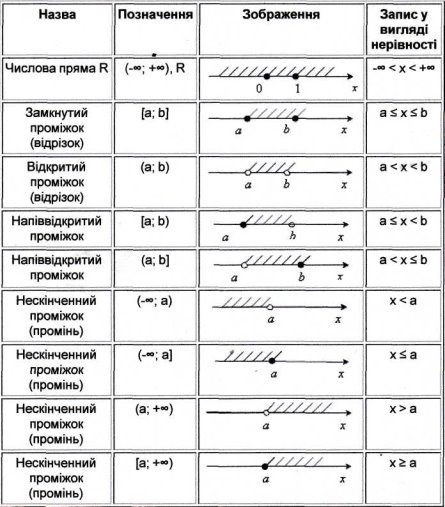
Розв'язування нерівностей, як правило, зводиться до зміни даної нерівності нерівністю, яка їй рівносильна.

Рівносильні нерівності

Нерівності, які мають одні й ті самі розв'язки, називають рівносильними. Нерівності, які

не мають розв'язків, також вважають рівносильними.

Нерівності мають такі властивості:

1.    Якщо з однієї частини нерівності перенести в другу доданок з протилежним знаком, то одержимо рівносильну їй нерівність.

Наприклад, нерівність х + 2 > 3 рівносильна нерівності х+2-2>3-2, тобто х > 1.

2.    Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то одержимо рівносильну їй нерівність.

Наприклад, — х > 3 рівносильна нерівності — х • 2 > 3 • 2 тобто х > 6.

3.   Якщо обидві частини нерівності помножити або поділити на одне й те саме від'ємне число, змінивши при цьому знак нерівності на протилежний, то одержимо рівносильну їй нерівність.

Наприклад, нерівність -2х < 10 рівносильна нерівності -2х:(-2) > 10: (-2), тобто х > -5.

V. Інтерактивна вправа

Інтерактивна частина уроку проводиться шляхом застосу­вання технології «Ажурна пилка». (слайд 5)

              На попередньому уроці вчитель роздав кожному учневі картку певного кольору з номером на ній (від 1 до 4). Сформува­лося п'ять груп по чотири особи у кожній. Групи отримали певні завдання (слайд 6):

•    «червоні» — розглянути метод рівносильних перетворень розв’язування нерівностей та пояснити  цей метод на прикла­дах;

•   «сині» — розглянути метод інтервалів розв’язування нерівностей та пояснити  цей метод на прикла­дах;

•   «жовті» — розглянути метод застосування властивостей функцій  розв’язування нерівностей та пояснити  цей метод на прикла­дах;

•   «зелені» — розглянути метод заміни змінних розв’язування нерівностей та пояснити  цей метод на прикла­дах.

Інструктування – вчитель розповідає учасникам про мету вправи, правила, послідовність дій і кількість часу на виконання завдань (роздає пам’ятку «Ажурна пилка» ) (слайд 7) ; запитує, чи все зрозуміло учасникам(2-3хв)

Пропонується такий поря­док роботи:

а)  підготовка до інтерактивної вправи. Учитель просить уч­нів пригадати, хто до якої групи належить, і зібратися кожній групі в певному місці. Кожний отримує картку червоного, си­нього, зеленого або жовтого кольору з номером своєї домашньої групи (1 хвилина);

б)  робота в «домашніх» групах. Учні повторюють та обгово­рюють методи розв’язування нерівностей, приклади розв’язаних нерівностей (2 хвилини);

в)  робота в «експертних» групах. Учні розходяться по різних групах відповідно до кольору своєї картки: «червоні», «сині», «зелені», «жовті». У кожній з груп опиняються учні, що володі­ють інформацією про певний метод. Кожна «ек­спертна» група вислуховує по черзі представників кожної «до­машньої» групи, отримує повну інформацію про кожен метод розв’язування нерівностей (8 хвилин);

г)  повернення в «домашні» групи. Кожен ділиться інформа­цією, отриманою в «експертних» групах. Інформація узагаль­нюється. Учасники допомагають один одному з'ясувати незро­зумілі моменти (5 хвилин);

д)  колективна робота. (слайд 8) Колективне розв’язання нерівностей:

1)   (х² – 7х + 12)² – 6(х² – 7х + 13) + 6 0(метод заміни змінної);

2)   + 6 (застосування властивостей функцій) ;

3)   ( х – 1 ) 0 ( метод рівносильних перетворень) ;

VІ. Підведення підсумків, оцінювання результатів уроку

Рефлексія(слайд 9)

На уроці ви добре попрацювали, продемонстрували знання, активність, добре мислили.

А тепер давайте оцінимо вашу роботу на уроці.

• Що робили на уроці?
• Які методи розв’язування нерівностей ми розглянули?
• Чи досягли очікуваних результатів особисто, клас в цілому? Чому ви так вважаєте?
• Що сподобалося вам при роботі в технології «Ажурна пил­ка»?
• Що можна було організувати краще? Корисніше?
• Які труднощі виникали у вас протягом уроку?
• Що тобі допомогло подолати труднощі?     (Опорні конспекти, підказки товаришів …).
• Що ви порадите однокласникам для подолання таких труднощів?
•  Над якими навичками, вміннями ще треба працювати?
• Що навчилися під час уроку?
• Що ви відчували під час роботи?

Учитель пропонує учням оцінити свою роботу на уроці, ви­ставивши собі від 0 до 3 балів за кожним з критеріїв. (слайд 10)

1.  Я активно працював(ла) у групі — ...

2.  Я вносив(ла) вдалі пропозиції, що були враховані гру­пою —...

3.  Я допомагав(ла) іншим учасникам, заохочував(ла) їх до роботи — ...

4.  Я узагальнював(ла) думки інших та просував(ла) робо­ту групи вперед — ...

Кілька учнів за бажанням називають і обґрунтовують власні оцінки (3 хвилини).