Урок алгебри 11 клас
Урок алгебри 11 клас
Загальні компетентності повинні сформуватися в процесі навчання та містити знання, навички, досвід співвідносин, досвід діяльності. Всі компетентності взаємозалежні і пов’язані між собою, тому формувати їх ізольовано одну від одної на різних етапах уроку не можливо. Компетентнісно орієнтоване навчання передбачає виконання учнями та учителем на уроках відповідних дій. Сучасні освітні технології та інтерактивні методи навчання, які формують ключові компетентності, надають навчанню природний характер, сприяють створенню в школі для дитини комфортного місця для активного громадського життя, а навчальна діяльність стає засобом реалізації потенціалу учня та розвитку особистих здібностей від рівня освітнього стандарту до творчості.
Тема: Дослідження функції за допомогою похідної та побудова її графіка
Мета: формувати вміння досліджувати функції за допомогою похідної та будувати їх графіки;
сприяти розвитку навичок самоконтролю знань з комп'ютерною підтримкою;
сприяти розвитку навичок спілкування в малій групі; формувати вміння аналізувати
виховувати вміння працювати в колективі; пізнавальний інтерес.
Тип уроку: засвоєння нових знань.
Вид уроку: урок із застосуванням інформаційних технологій.
Дидактичне забезпечення та обладнання уроку: завдання для самостійної роботи, тести, бланки самооцінювання, комп'ютер, мультимедійний пристрій.
ХІД УРОКУ
- Організаційний етап.
Починаємо наш урок. Сьогодні я хочу надати вам можливість оцінити свої знання самостійно. У кожного на робочому місці бланк самооцінювання, який ви заповнюватимете протягом уроку. (Учні ознайомлюються з бланком самооцінювання.)
ІІ. Перевірка домашнього завдання
Перевірку домашнього завдання здійснюємо за допомогою мультимедійного пристрою.
На екрані висвітлюється правильний варіант розв'язання завдання.( Слайд 1)
Тестові завдання
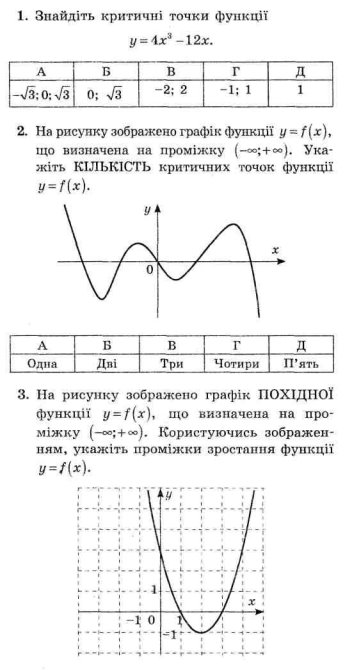
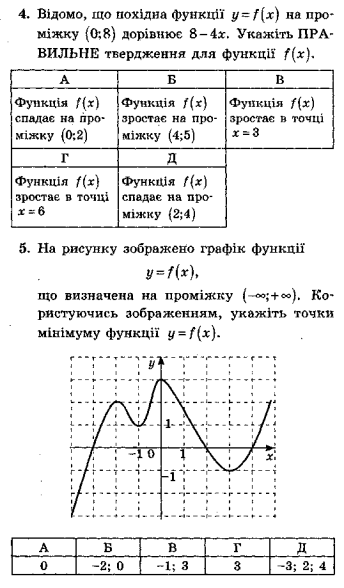
Відповідь: 1-г, 2-г, 3-б, 4-д, 5-в.
ІІІ. Актуалізація опорних знань. Підготовка до вивчення нової теми
Теоретична розминка
( В ході теоретичної розминки діти проводять взаємоопитування та взаємоперевірку. Такий вид діяльності стимулює спілкування учнів із ровесниками з метою підвищення рівня навчальних досягнень та ерудиції учнів.)
Запитання для усного опитування учнів першого ряду до учнів другого ряду
1. Що таке область визначення функції?
2. Як знайти координати точок перетину графіка функції з координатними осями?
3. Яку функцію називають парною? Наведіть приклад парної функції.
4. Яку функцію називають непарною? Наведіть приклад непарної функції.
5. Яку функцію називають періодичною? Наведіть приклад періодичної функції.
6. Як знайти критичні точки функції?
7. Що таке проміжки монотонності функції?
8. Яку точку називають точкою максимуму?
9. Яку точку називають точкою мінімуму?
Запитання для усного опитування учнів другого ряду до учнів першого ряду
1. Як знайти область визначення функції?
2. Як знайти нулі функції?
3. Як з'ясувати парність функції? Що можна сказати про графік парної функції?
4. Як знайти проміжки монотонності, застосовуючи похідну?
5. Яку точку називають критичною?
6. Як знайти точки екстремуму?
7. Чи кожна критична точка є точкою екстремуму?
8. Наведіть приклад періодичної функції. Чому ця функція є періодичною?
9. Наведіть приклад парної функції. Чому ця функція є парною?
IV. ПОВІДОМЛЕННЯ ТЕМИ УРОКУ. ЦІЛЬОВА УСТАНОВКА. МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ
Ми пригадали властивості функції та як їх визначати. Усе це нам потрібно для того, щоб навчитися досліджувати функцію, використовуючи похідну, та будувати її графік. На уроці ми будемо вчитись застосовувати властивості функцій до їх дослідження та побудови їх графіків. (Учні записують тему уроку).
V. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Колективна робота ( Метод «Антивірус»)
(Цей метод використовують під час ознайомлення з алгоритмом дослідження, технології, дій. На дошці в довільному порядку («уражена вірусом інформація») розташовані картки з назвами етапів. У процесі колективного обговорення учасники визначають ймовірну послідовність етапів («лікування від вірусу»). Асистент розташовує картки в запропонованому порядку. Перевірка правильності вибору відбувається за допомогою методу «Програмованого контролю». )
На дошці в довільному порядку («уражена вірусом інформація») розташовані картки з назвами етапів дослідження функції. Розташуйте основні властивості функції у вигляді алгоритму так, щоб у найзручніший спосіб можна було дослідити властивості будь-якої функції
У процесі колективного обговорення допоможіть визначити ймовірну послідовність етапів («лікування від вірусу»). (Розташовуємо картки в запропонованому порядку. Перевірка правильності вибору відбувається за допомогою методу «Програмованого контролю», тобто з використанням підручника.
Метод «Програмований контроль». Цей метод дозволяє виявити учасників, які припустилися помилки в означенні. Кожен учень перевіряє справедливість зробленого вибору. (ст..80, §10)
(Ці методи розвивають вміння працювати з підручником, опрацьовувати математичні тексти, використовувати додаткову інформацію, критично оцінювати здобуту інформацію та її джерела, виокремлювати головне, аналізувати, робити висновки. )
Схема дослідження функції
1. Знайти область визначення функції.
2. Визначити парність та періодичність функції.
3. Знайти координати точок перетину графіка функції з координатними осями.
4. Знайти критичні точки функції. Знайти асимптоти, якщо вони існують.
5. Знайти проміжки монотонності функції.
6. Знайти точки екстремуму функції.
7. Якщо необхідно, знайти координати додаткових точок.
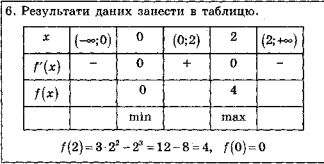
8. Результати даних занести в таблицю і побудувати графік функції
2. Колективне розв'язування вправ
Кожен етап розв'язання учитель проектує у вигляді слайдів і пояснює. Учні записують розв'язання в зошити.
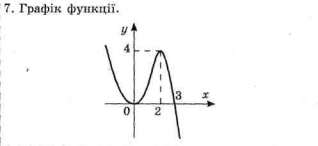
Дослідіть функцію ƒ(х) = 3х2 -х3 і побудуйте її графік.
- Область визначення ƒ(х) = R, оскільки 3х2 -х3 — многочлен
2. Визначаємо парність функції
ƒ (-х) = 3(- х) 2-(-х3 )= Зх2 + х3
Функція не є ні парною, ні непарною, неперіодична.
- Знайдемо точки перетину графіка функції з осями координат
Ох: у=0, то х=0, х=3 ; (0;0), (3;0)
Оу: х=0, то у=0 (0;0),
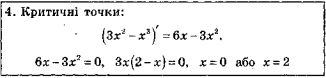
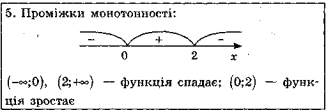
Слайд10
3. Історична хвилинка
Учні підготували повідомлення про вчених математиків, які займалися диференціальним численням. Портрети вчених проектуємо на екран за допомогою мультимедійного пристрою.
Лейбніц Готфрід Вільгельм (1646-1716)
Німецький математик, фізик, філософ, юрист, історик, конструктор-винахідник, мовознавець.
Основні математичні роботи присвячені розробці диференціального та інтегрального числення. Окремі та розрізнені прийоми дослідження функції звів до єдиної системи взаємопов'язаних понять аналізу. Дав означення диференціала та інтеграла, екстремальних точок і точок перегину. Встановив взаємно обернений характер основних операцій аналізу — диференціювання та інтегрування. Розробив правила диференціювання суми, різниці, добутку, частки, степеня, неявної функції. Йому належать формула для багаторазового диференціювання добутку (формула Лейбніца) і правила диференціювання найважливіших трансцендентних функцій.
Лейбніц увів багато математичних термінів, які ввійшли в наукову практику: функція, диференціал, диференціальне числення, диференціальне рівняння, алгоритм, абсциса, ордината, координата, а також символи похідних, диференціала та інтеграла.
Кравчук Михайло Пилипович (1892-1942)
Михайло Пилипович Кравчук, доктор фізико-математичних наук, професор. Народився на Волині, у селі Човниця Ківерцівського району, в сім'ї землеміра. Закінчив Луцьку гімназію із золотою медаллю і Київський університет з дипломом першого ступеня. Перші наукові роботи опубліковані були ще за студентських років. Він отримав важливі результати в алгебрі і теорії чисел, теорії аналітичних функцій, теорії функцій дійсної змінної, теорії ймовірностей і математичній статистиці. Важливе місце в діяльності Кравчука М. П. мали дослідження з теорії диференціальних і інтегральних рівнянь, він написав двотомну монографію «Застосування способу моментів до розв'язання диференціальних рівнянь». Його наукові праці сприяли активному застосуванню диференціального та інтегрального числення в різних сферах прикладної математики і фізики. Написав низку робіт з історії математики, підручники для вищих навчальних закладів.
Гра « Знайди пару»
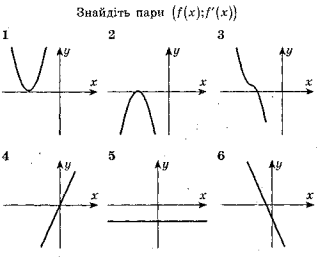
Відповідь. (1; 4), (3; 2), (6; 5)
- Робота в групах (створюються групи по 4-6 учнів)
Учні працюють у зошитах: досліджують властивості функції і будують графік; заносячи дані в картку самостійної роботи за варіантами, запропонованими вчителем. Після виконання завдання проводиться представлених розв’язань на дошці з детальним поясненням.
VІ. Підсумок уроку
1. Які відкриття для себе ви зробили під час сьогоднішнього уроку?
2. Яку ви бачите перспективу застосування отриманої інформації у своїй діяльності?
VІІ. Домашнє завдання
§10 Вправа 365 (а, в)

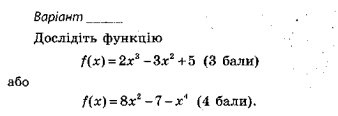

VІ. Підсумок уроку
1. Які відкриття для себе ви зробили під час сьогоднішнього уроку?
2. Яку ви бачите перспективу застосування отриманої інформації у своїй діяльності?
VІІ. Домашнє завдання
§10 Вправа 365 (а, в)
Література
1. Бібік Г. Компетентнісний підхід у навчанні математики як методична проблема // Наукові записки: Педагогічні науки. - Вип. 82 (1). — Кіровоград, 2010.
2. Раков С. А. Формування математичних компетентностей учителя математики на основі дослідницького підходу в навчанні з використанням інформаційних технологій: Автореф. дис. докт. пед. наук: 13.00.02. — К., 2005. — 52 с.
3. Родигіна І. В. Компетентісно орієнтований підхід до навчання. — X. : Вид. група «Основа», 2005. — 96 с.
4. Юр'єва К. Зміст і шляхи формування полікультурної компетентності педагогів // Управління школою. — 2004. — № 33, — С. 10-11.
5. Солодченко Л.О. Розвиток життєвих компетентностей на уроках математики.- Т.-Х. : Ранок, 2011.
6. Державний стандарт базової і повної загальної середньої освіти. // К.: Постанова Кабінету Міністрів України № 1392 від 23.11.2011.
7. Ткаченко О., Кожевнікова М. Формування компетентностей на уроках математики//Математика в школах України. – Х., 2014. – №6. – С.2-3.
8. Бевз В. Г. Використання історизму у шкільному курсі математики: Практикум з історії математики: Навчальний посібник. - К.: НПУ імені М. П. Драгоманова, 2009.


про публікацію авторської розробки
Додати розробку
