Методи розв'язування прикладних задач на уроках математики.

                                                                    Ольга Овчар, вчитель методист

                                                                  СЗШ №67 м.Львова

Методи розв'язування прикладних задач на уроках математики.

В даній статті, на основі досвіду роботи, дано рекомендації щодо розв’язування прикладних задач на уроках математики в 5-6-х класах.

Математика розвиває мислення учнів: абстрактне і логічне, необхідні людині для засвоєння нових знань та полегшення адаптації до умов життя, що постійно змінюється; алгоритмічне, що передбачає сформованість умінь діяти відповідно до заданих алгоритмів, а також конструювати нові способи дій. Ці якості потрібні як тим учням, яких цікавлять мови, мистецтво та художня творчість, так і тим, які мріють займатися спортом, майбутнім історикам, юристам, медикам, не кажучи вже про тих, хто в майбутньому планує займатися математикою.

      Формування творчого мислення учнів є завданням усіх шкільних дисциплін, проте математика посідає в цьому чільне місце. Справді, чітка логічна схема міркувань, точність лаконічність мови, систематична послідовна аргументація - усе це властиве процесу навчання математики і сприяє вихованню розумової культури учнів. Розвиток логічного мислення, що здійснюється   на   уроках   математики,   впливає   на   успішне вивчення всіх предметів, у тому числі гуманітарних.

Викладаючи математику, ми намагаємося по­казати учням її місце і можливості  у цьому про­цесі. Учитель математики може ознайомити учнів із розв'язанням деяких типів прикладних задач у процесі вивчення відсотків, пропорції, лінійної функції, елементів прикладної математики, ариф­метичної та геометричної прогресій, показникової та логарифмічної функцій, похідної. Прикладні задачі шкільної програми з математики  можна розбити на такі типи задач:

1.     прикладні задачі з математики;
2.     задачі на пропорціональні величини;
3.     задачі, які розв’язуються складанням рівнянь або системи рівнянь;
4.     оптимізаційні задачі;
5.     задачі на знаходження відсоткових розрахунків, знаходження прибутків, нагромадження капіталу.
6.     прикладні задачі з використанням похідної;
7.     задачі, які використовуються в процесі вивчення показникової і логарифмічної функції;
8.     прикладні задачі у сімейному бюджеті;
9.     задачі в комбінаториці та в теорії ймовірності;
10. задачі і міжпредметні  зв’язки;
11. задачі на розчини та суміші,
12.  прикладні задачі, які розв’язуються за допомогою формул прогресій.

Не виникає сумніву, що найефективнішим способом розвитку математичної діяльності учнів є розв’язування  задач, особливо прикладних. Саме завдяки їм учні починають цікавитися математикою. На уроках математики навчальний процес іде здебільшого від практичних задач до теорії, а потім від теорії – до практики.

Перехід від задачі до теорії нерідко створює проблемну ситуацію. Саме за допомогою задач слід підводити учнів до усвідомлення доцільності вивчення теорії. Взаємозв’язок з практикою можна розглянути за таким планом:

1.               Прикладна задача.
2.               Математична модель прикладної задачі.
3.               Теоретична задача.

Насамперд, слід показати учням, як за допомогою прикладної задачі створити проблемну ситуацію, як задача не математичного змісту набирає математичного характеру. 

Тема ,,Подільність чисел’’ має важливе значення в курсі математики. Під час вивчення цієї теми учні знайомляться з новими властивостями чисел, дізнаються багато цікавого. Знаючи властивості найбільшого спільного дільника (НСД) і найменшого спільного кратного (НСК) можна оригінально розв’язувати деякі задачі. Корисно показати учням застосування понять НСД і НСК при розв’язуванні прикладних задач.

Задача 1. Зубчаста передача верстата складається з трьох шесте­рень різного діаметра; дві з них мають 15 і 25 зубців. Скільки зубців повин­на мати третя велика шестірня, щоб при одному її оберті інші поверну­лись ціле  число разів?[4] 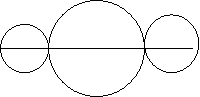Рис.1                                                                  Розв'язання. До чисел 15 і 25 підберемо кратні їм числа. Дістаємо запис:

На 15 діляться 15, 30, 45, 60, 75, 90, 105... .

На 25 діляться 25, 50, 75, 100, 125... .

Бачимо, що у цих рядах чисел перше число, яке ділиться на 15 і 25  - 75. Отже, велика шестірня повинна мати 75 зубців, щоб при   одному   її   оберті   кожна   з   малих   повернулась   ціле   число   разів. Розв’язування задачі зводиться до знаходження НСК чисел 15 і 25.

Задача 2. Повз залізничну станцію проходять один за одним три по­їзди: у першому 418 пасажирів, у другому 494, в третьому 456. Скільки па­сажирських вагонів у кожному поїзді, коли відомо, що в кожному вагоні однакове число пасажирів і їх число — найбільше з усіх можливих?[4]

Розв'язання. Щоб знайти число вагонів у кожному поїзді, треба число пасажирів кожного поїзда (дано в умові) поділити на число пасажирів у вагоні кож­ного поїзда (це число невідоме).

За умовою задачі у кожному вагоні трьох поїздів однакове число паса­жирів, тобто це число — спільний дільник чисел 418, 494 і 456, притому най­більший. Отже, спочатку знаходимо НСД чисел 418, 494 і 456, потім на знайдене число ділимо 418, 494, 456. Знайдемо НСД  чисел 418, 494 і 456: 418 = 38 • 11, 494 =38 •13; 456 = 38 • 12. Отже, НСД (418, 494 і 456) = 38. Звідси в першому поїзді 11   вагонів, в другому 13, в третьому 12.

Задача 3. Два лижних загони йшли з однаковою швидкістю; один про­йшов 112 км, другий 96 км. Скільки часу йшов кожний загін, якщо їх швид­кість була найбільша з усіх можливих швидкостей, що виражаються числом цілих кілометрів за годину?

Розв'язання. Щоб знайти число годин руху кожного загону, треба відстань, яку про­йшов кожний загін, поділити на швидкість руху за годину. За умовою швид­кість обох загонів однакова, вона виражається цілим числом кілометрів, отже, швидкість за годину — це найбільший спільний дільник 112 і 96. Знайдемо НСД (112; 96); 112 =2  • 2 • 2 • 2  •  7; 96 = 2 • 2 • 2 • 2  • 2 • 3; НСД(112; 96) = 2 • 2 • 2  • 2 =16; число годин руху першого загону - 7і другого – 6 годин.

Задача  4. О 7-й годині ранку 3 автобуси виходять з площі в трьох напрямах; перший повертається через 2 год І0 хв і через 20 хв виходить знов, дру­гий повертається через 1 год 48 хв і виходить знов через 12 хв; третій повертається через 1 год 36 хв  і виходить знов через 4 хв. О якій годині вони знов одночасно вийдуть з площі?

Розв'язання. Спочатку визначимо, скільки часу витрачає кожний автобус на один пробіг і зупинку: перший автобус 2 год 10 хв + 20 хв  = 150 хв; другий  - 1 год 48 хв +12 хв =120 хв; третій 1 год 36 хв + 4 хв = 100 хв Потім знайдемо, через скільки часу вони знов усі одно­часно вийшли з площі. Шуканий проміжок часу ділиться націло на 150, 120 і 100, тобто є НСК (150, І20 і 100). Воно дорівнює 600 хв, або 10 год. Але автобуси вийшли о 7-й год. ранку, отже, знов вийдуть одночасно о 7 год + 10 год = 17 год, або о 5-й годині вечора.

Задача 5. Чотири пароплави відходять від пристані в одному напрямі: ­
перший — через кожні 5 днів, другий — через кожні 8 днів, третій — через
кож­ні 12 днів, четвертий — через кожні 15 днів. Через скільки часу вперше зу­стрінуться на цій пристані перший пароплав з другим, з третім і
четвертим, другий з третім, всі чотири разом?
Розв'язання. Число днів, через яке зустрінеться перший пароплав (він повертається через 5 днів) з другим (повертається через 8 днів) повин­но ділитися на 5 і на 8, тобто НСК (5 і 8) = 40 (днів); пер­ший пароплав з третім зустрінуться через число днів, що дорівнюватиме НСК (5 і 12) =60 (днів), перший з четвертим — через 15 днів (НСК (5 і 15)). другий з третім — через 24 дні (НСК( 8 і 12)), всі чотири пароплави зустрі­нуться через 120 днів (НСК (5, 8, 12 і 15)).[4]

Задача 6. Мала шестірня велосипеда має 8 зубців, велика 18 зубців. Яке най­менше число обертів повинна зробити педаль, щоб заднє колесо і велика шестірня повернулись у своє початкове положення?

    Розв'язання. До початку руху можна відмітити два зубці, які за­ймають однакове положення на обох шестірнях. Ці два зубці займуть знов те саме положення, коли обидві шестірні повернуться на однакове число зубців. Це число ділиться на 8 і на 18, тобто є спільним кратним 8 і 18. Отже, знайдемо НСК (8, 18) = 72; 72:8 = 9 — число обертів меншої шестірні. 72 : 18 = 4 -  число  обертів   більшої   шестірні.

    Повторивши з учнями на цілих числах, як змінюється сума із зміною доданків, вчитель  може запропонувати приклади і задачі на зміну суми дробів. Напри­клад:

1. Як зміниться межа прямокутного поля, якщо його довжину збільшити

на 2   км, а ширину на 1 км?

2. Турист повинен  був  пройти  за  3 дні певний  маршрут,  але  пройшов

за перший день на 6 км, більше, за другий — на 7км менше і  за третій — на 2 км більше, ніж повинен був проходити за кожний з цих днів.

На  скільки  пройдена відстань більша  чи  менша  від запланованої?

Так само можна повторити на дробових числах зміну різниці. Наприклад, роз­в'язати задачі:

  3. В  одному ящику на 7кг чаю  більше,  ніж у другому. Яка буде різниця між кількостями чаю, якщо 1) перекласти 3 кг чаю з першого ящика в другий? 2) перекласти 2 кг чаю з другого ящика в перший?

   4. Бронза містить частини міді, решта – олово і свинець. Скільки важить злиток, якщо в ньому 1 кг міді?

   Розв'язання. х=1; х=2 кг

      Кожній людині у житті доводиться мати справу не стільки з готовими задачами, рівняннями, нерівностями, формулами, скільки виражати реальні залежності між явищами і величинами.  Для кращого засвоєння теми ,,Дії із звичайними дробами” треба розв’язувати з учнями велику кількість вправ, приділяючи особливу увагу задачам прикладного змісту. Наприклад:

1. 1 дм³ льоду важить 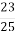кг. Знайти вагу дм³ льоду.
2. Літак пролітає 360 км/год. Яку відстань він пролетить за 6 год? за 2 год? за 1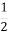год? за год? за год? за год?
3. Насіння льону містить 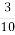частини ( за вагою) жиру. Скільки жиру в 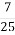т насіння льону, які взято для виготовлення масла?
4. Відро води важить приблизно 12 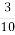кг. Скільки важить вода, що наповнює відра?

При вивченні теми ,,Десяткові дроби. Дії з десятковими дробами” можна використати такі завдання, умови яких подані нижче:

1. Треба виготовити 2 болти, один довжиною 7,2 см, другий довший на 12,9 см. Якої довжини треба взяти стальний прут, коли вважати, що 0,9 см буде втрачено при різанні?
2. Вранці до початку роботи температура приміщення була 12,3, до моменту початку роботи було 15,5. На скільки градусів підвищилась температура приміщення?
3. На заготівельний пункт привезли спочатку 297,8 т зерна, потім ще на 57,5 т більше, ніж першого разу. Скільки всього зерна привезли на заготівельний пункт?
4. Деталь машини, що важила 12 кг, робітник запропонував замінити деталлю, вага якої була менша на 0,25 ваги першої. Яка була вага легшої деталі?
5. Один пасічник одержав в середньому по 40,5 кг меду з вулика, другий – на 0,6 цієї ваги більше. Скільки меду одержав у середньому другий пасічник з одного вулика?

З задачами, розв’язування яких зводиться до складання пропорцій, ми зустрічаємося дуже часто і не тільки в математиці. В задачах на відношення чи пропорцію явно чи неявно ставиться питання про пропорційність величин. Особливу увагу потрібно звернути на прикладну спрямованість теми, звертаючись до задач навколишнього життя. На застосування пропорції розв’язуються задачі на суміші, сплави, розчини, спільну роботу, витрати зарплати і інші. Головне не тільки в умінні розв’язувати задачі за готовим текстом, але й в умінні відповідати на практичні питання у вигляді задач, у яких є не всі дані. Такі задачі розвивають в учнів логічне мислення, привчають їх користуватися додатковими матеріалами. Деякі задачі подані в підручниках коротко, надто лаконічно, тому корисно пояснити їх учням описово, включаючи в них елементи новизни. Це сприятиме активізації розумової діяльності учнів, викликатиме продовжити бесіду після розв’язання задачі.[2]

     Задача 1.   1   кг цукерок коштує 20 грн.   Скільки  треба  заплатити   за 825 г цих цукерок?

У цій задачі спосіб зведення до одиниці  (1 г коштує...)  або оберненого

зведення до одиниці   (формула  розв’язання  була б 825: ) менш зручні, ніж зведення до кратних частин  (825 = 500 +250 + 50 + 25, звідки  вартість цукерок дорівнює  1000+500+ 100 +50 =1650, тобто   16 грн  50  коп).

Крім   того,   цю  задачу   можна   звести   до   знаходження   дробу   від   числа і пропорціональної зміни: 825 г = кг; знайдемо від ціни 20 грн; 20•=1650 (коп)= 16 грн 50  коп.

Задача 2. Рисунок предмета зроблений у масштабі ; відстань між двома його точками дорівнює 4,8 см. Яка відстань буде між цими точками на другому рисунку, який зроблено в масштабі   ?

Запишемо умову, позначивши через х см відстань між точками на дру­гому рисунку:     -   4,8 см

                           -    х см

Довжина лінії на рисунку прямо пропорціональна числовому масштабу, тому дістаємо пропорцію: х: 4,8 = :^;   х=4,8 •  :=2,56 (см).

Задача3. При семигодинному робочому дні певне замовлення можна виконати за 18 днів. За скільки часу можна ви­конати те саме замовлення, якщо працювати щодня по 2 год понаднор­мово?

Умову записують у вигляді таблиці:

                                 7 год за день   -   18 днів

                                  9 год за день    -    х днів

Учні розв'яжуть її так:

1) 7• 18 = 126   (робочих годин потрібно для  виконання роботи);

2) 126:9=14 (днів потрібно буде для виконання замовлення, якщо
працювати щодня по 7 + 2 = 9 год на день).

ІІ спосіб – спосіб пропорції. Це обернено пропорціональна залежність.

х=7 •18:9=14 (днів).

Задача 4. 36 робітників, працюючи по 7 год  на день, закінчили ро­боту за 20 днів. За скільки днів ту саму роботу виконають 40 робітників, працюючи по 6 год на день?[3]

Шукана величина — число днів роботи — обер­нено  пропорціональна   числу  робітників   і   тривалості   робочого  дня.

Запис умови:  36 робітн. 7 год. 20 днів

                         40 робітн.  6 год.  х  днів

Задачу розкладають на дві задачі. Припустимо, що 40 робітників пра­цювали також по 7 годин. Тоді число днів повинно змінитися тільки в залеж­ності від числа робітників. Дістаємо задачу:

36 робітн. виконають роботу за 20 днів

40   робітн. виконають роботу за   у  днів

Невідоме число позначаємо через у; воно не є шуканим задачі, бо не відповідає всім її умовам. у менше 20 в стільки разів, у скільки разів 36 менше 40: у : 20 = 36 : 40 (обернена пропорційність). Звідси,  у = 18 (днів)

Змінюємо     число     годин     щоденної     роботи     відповідно     до     умови. При   7-годинному  робочому дні  роботу  можна  виконати  за 18 днів. При   6-годинному  робочому дні роботу можна виконати за х днів. х:18 =7:6  (обернена пропорціональність), х=21(день)

       Задача 5.  З сушених яблук по 16грн. 50 коп. за 1кг. і слив по 18грн. 50коп. за 1кг. склали 12 кг. суміші, ціною по 17 грн. за 1кг. Скільки кілограм яблук і скільки кілограм слив увійде в суміш?

Розв'язання: 1кг яблук коштує 16,5 грн. Якби магазин продавав по ціні суміші, то мав би прибуток: 17-16,5=0,5(грн) 1кг. слив коштує 18,5 грн. Якби магазин продавав по ціні суміші, то мав би збиток: 18,5-17=1,5(грн)
 

 

Яблука по 16,5 грн.                                      +0,5 грн.     х₁

               17грн.
Сливи по 18,5 грн.                 -1,5 грн.            х₂

Щоб не мати ні збитку, ні прибутку, потрібно взяти кількості змішу­ваних фруктів обернено пропорційно числам, що виражають збиток і прибуток.

х₁: х₂=1,5:0,5=3:1

х₁=3=9(кг)- яблук,        х₂=1=3(кг)- слив.

Задача  6. Куплено борошно трьох сортів. Першого 5 кг по 5 грн 60 коп, другого 7кг по 4 грн 60 коп за кілограм і 3 кг третього сорту. За доставку про­дуктів заплатили 2 грн 80коп. Один кілограм купленого борошна в се­редньому коштував  5 грн. Скільки коштував один кілограм борошна третього сорту ?

Розв'язання: 1. 7+5+3=15(кг) – всього куплено кілограмів борошна.

2.  5∙15=75(грн) - заплатили б за борошно по ціні 5 грн за 1кг.

 3.  75 +2,8 =77,8(грн ) – вартість борошна з доставкою.

4.  5,6 ·5= 28(грн.) - коштує 5кг борошна першого сорту.

5.  5,6 ·7=32,2( грн.) - коштує 7кг борошна другого сорту.

6.  28 +32,2=60,2(грн.) - заплатили за борошно першого і другого сорту разом.

7.  77,8 - 60,2= 17,6(грн.) – вартість 3 кг третього сорту.

8.  17,6 :3=5,87( грн.) - коштує один кілограм борошна третього сорту.

Задача 7. У саду на двох ділянках посадили 224 штуки розсади полуниць. Визначити, скільки штук розсади посадили на кожній ділянці, якщо площа першої ділянки 8 м², а площа другої 24 м².(На кожному квадратному  метру землі садять розсаду в середньому порівну).

Розв'язання: Спочатку визначимо площу двох ділянок разом: 8+24=32 (м²).

Визначимо скільки штук розсади припадає на 1 м²: 224:32=7(штук).

Обчислимо число штук розсади на 8 м² і на 24 м²: 7·8=56(штук),  7·24=168(штук).

Задача 8.За три ящики мила одного й того самого сорту заплатили 400 грн. Скільки заплатили за кожний з них, якщо перший важив 20 кг, другий 30 кг і третій 50 кг?

 У цій задачі потрібно поділити 400 грн на 3 частини пропорційно вазі окремих ящиків мила.

Скористаємось правилом, виведеним при розв’язанні попередньої задачі.

;;

Задача  9. Визначити квартирну плату за кожну з двох кімнат (8 м² і 24  м²), якщо за обидві разом потрібно заплатити 64 грн.

Позначимо плату за 1 м²  - х грн; тоді за першу кімнату треба заплатити 8х грн, за другу - 24х грн. Разом 64 грн.

Складаємо рівність: 8х + 24х = 64, х = 2 грн. Квартирна плата за одну кімнату 8·2=16( грн), за другу - 24·2=48 ( грн).

Висновок.

       Кожній людині у житті доводиться мати справу не стільки з готовими задачами, рівняннями, нерівностями, формулами, скільки виражати реальні залежності між явищами і величинами за допомогою формул, рівнянь та нерівностями. Тому важливо, щоб учні не лише оволоділи алгоритмом розв’язування тих чи інших задач, а й знали, як вони виникають. Розв’язування прикладних задач дуже корисне, воно сприяє розвитку в них уміння нешаблонно мислити, з інтересом підійти до розв’язування задач, спонукає до складання нових задач, до ускладнення умов, систематизує відомі знання й досвід, тобто сприяє всебічному розвитку математичного мислення.

       Використовуючи активні методи навчання у формуванні вмінь і навичок учнів у процесі розв’язування задач прикладного змісту при вивченні шкільного курсу математики, учитель повинен прагнути, щоб учні краще аналізували, співставляли, узагальнювали, робили правильні висновки,  вміло застосовували набуті знання на практиці, щоб у них підвищився інтерес до набуття математичних знань. Тобто, розв’язування прикладних задач на уроках математики дає позитивні результати.

1. Зайцева Л.І. Математична компетентність, диференційний підхід. Палітра педагога. №2, 2004.
2. О. Овчар. ,,Застосування пропорцій до розв’язування задач’’, журнал  ,,Молодь і ринок’’, №3(38), березень 2008, ст.118-121.
3. Рахматов Н.Х. ,,Иллюстрация математических методов на прикладных задачах’’, журнал  ,,Математика в школе’’, №2, 1989, ст.. 30-35.
4.  Чекмарьов Я.Ф. Методика навчання арифметики в школах робітничої молоді. Київ ,,Радянська школа’’, 1961, стст.165-166.