Методические рекомендации по изучению темы: ”Иррациональные уравнения”.

Методические рекомендации по изучению темы:

”Иррациональные уравнения”.

(разработала учитель математики ООШ №10 г.Славянска Пилипенко В.Ю.)

Справочный материал

 

1. Уравнение, содержащее неизвестное под знаком радикала, называется иррациональным; например; например, 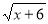= 2, 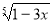= 3 – иррациональные уравнения.
2. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путём возведения в степень обеих частей уравнения или замены переменной.
3. При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует найти область допустимых значений переменной входящей в уравнение или проверить все найденные корни подстановкой в исходное уравнение.

Занятие 1

1. Решите уравнение:

- 1 - = 0.

Решение.

ОДЗ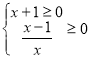          

 

Перенесём 1 в правую часть и возведём обе части в квадрат. Получим:

,    ,   ,

,    ,     ,    

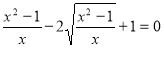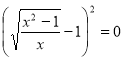Ответ:  ,       .

 

2. Решите уравнение:

 

Решение.

,   .

 

, ,

 

,, 

 

,  ,  ,  ,

  или , нет корней, т.к. -3<0.

 

Проверкой убеждаемся, что х = 2 и х = -2 корни данного уравнения.

Ответ: .

 

3. Решите уравнение:

 

.

Решение.

 ,

Применим формулу

 

,

 

,

 

      ,

 

(, 

 

,  .

 

Ответ: -2.

 

4. Решите уравнение:

    .

Решение.

ОДЗ ,       .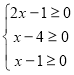

     

 

Возведём обе части в квадрат и получим:

       - посторонний корень.

Ответ: 5.

 

5. Решите уравнение:  

Решение.

 

 Применим формулу

,

, , (,

, ,

       или

- посторонний корень.

Ответ: 1.

 

6. Решите уравнение:

    

Решение.

  Применим формулу .

,          .

Ответ: 0.

 

7. Решите уравнение:

    

Решение.

   ОДЗ ,

      или 

                    .

- посторонний корень.

Ответ: -1;2.

 

Задания для самостоятельной работы.

Решите уравнения:

А) .                  Ответ: 4.

Б)                       Ответ: 0.

В)                 Ответ: 9.

Г)                    Ответ: 5.

Д)   Ответ: -2; 3,5.

 

Занятие 2

1. Решите уравнение:

 

Решение.

  Пусть >0.

  ,   , , 

Значит,   или  .

                             нет корней, т.к. -3<0.

       ,

        ,

Проверкой убеждаемся, что корень данного уравнения.

Ответ: 5.

 

2. Решите уравнение:

Решение.

Пусть Следовательно, по теореме Виета

Значит,             или     

                                         корней нет, т.к. -3<0.

              

              

Ответ:  2.

 

3. Решите уравнение:

     .

Решение.

ОДЗ при m – чётном <1, а при m – нечётном х – любое число.

Так как = 1 не является корнем уравнения, то   , пусть

по теореме Виета .

При m – чётном  ,

 

 

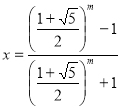При m – нечётном .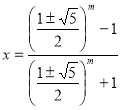

Ответ: при m – чётном  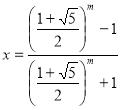, при m – нечётном .

 

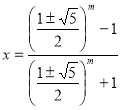4. Решите уравнение: 

        

Решение.

      .

       На промежутке   области определения данного уравнения функция f(х) =   является монотонно возрастающей, а функция g(х) = =  монотонно убывающей. Значит уравнение f(х) = g(х) имеет единственный корень.

Выполним замену . Тогда f(у+1)=и g(у+1)= =. Значит f(-у+1)= g(у+1). А так как по условию

f(у+1)= g(у+1), то f(-у+1)= f(у+1) или откуда Следовательно данное уравнение имеет корень х=1.

Ответ: 1.

 

5. Решите уравнение:

     .

Решение.

Пусть Значит, а .

Следовательно, ,

     

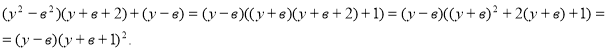
Значит, .       Следовательно, имеем

(.

          .      , 

Ответ: 0.

 

6. Решите уравнение:

    

Решение.

Пусть , , тогда .

Значит,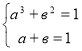          

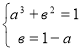
,   ,   ,   или , . Следовательно, .

Имеем, , . А значит, х = 2, х = 10, х = 1.

Ответ: 2;1;10.

Задания для самостоятельной работы.

А) .                   Ответ: 2,5.

Б)                      Ответ: 0,5

В)                         Ответ: 5.

Г)                   Ответ: 1;0.

Д)                  Ответ: 10.

 

Занятие3.

1. Решите уравнение:

    

Решение.

    Пусть

    Тогда  .

               

                .

 

Первый случай .                           

 Второй случай а>1.  

.

Ответ: 6.

 

2. Решите уравнение:

    

Решение.

      .

      

Первый случай  2.

       2-, .

 

Второй случай 2 < <3.

       , 1 = 1, значит 2 < <3, 4<x+1<9, 3<x<8.

Третий случай  3.

       - 2+ - 3 = 1,  2 = 6,   = 3,  х+1 = 9, х = 8.

Следовательно, 3x8.

Ответ: 3x8.

 

3. Решите уравнение:

     .

Решение.

     ,

     ,         

     ,  

     .    

Уравнение имеет решение лишь при условии , т.е. .

Тогда (при условии, что  ).

Значит,      , ,    или .

Проверкой убеждаемся, что  - посторонний корень.

Ответ: -2.

 

4. Решите уравнение:

    

Решение.

Первый способ.

     ОДЗ 

     т.к. , то  значит , .

Возведём обе части уравнения в квадрат

     ,  , по теореме Виета

, .

Проверка показывает, что - посторонний корень.

Ответ: 5.

Второй способ.

, слева возрастающая, а справа убывающая функции, непрерывные в ОДЗ Подбором определяем единственный корень

Ответ: 5.

 

 

5. Решите уравнение:

    

Решение.

    

Пусть , тогда

Возвёдем обе части уравнения в квадрат

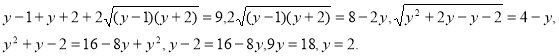
Вернемся к замене: , ,  ,

значит

Проверкой убеждаемся, что х = 1 – корень данного уравнения.

Ответ: 1.

 

6. Решите уравнение:

   

Решение.

    

 ОДЗ: 

 

Возведем обе части уравнения в квадрат.

,  .

  ,  , ,

,

Значит, проверим значения х=0 и х=1.

Пусть х=0, тогда . Следовательно х=0 – корень уравнения.

Пусть х=1, тогда , .

х=1 – посторонний корень.

Ответ: 0.

 

Задания для самостоятельной работы.

А)   .                                                     Ответ: .

Б)                                                    Ответ: 8.

В)                        Ответ: 7.

Г)                            Ответ: 0;3.

Д)                                    Ответ: .

 

Занятие 4.

1. Решите уравнение для всех а:

    

Решение.

 

  При всех а<0,нет решений, при а .

Ответ: .

2. Решите уравнение:

     .

Решение.

      .

ОДЗ ,     .

,   ,  

Возведем обе части последнего уравнения  в квадрат

,    ,   , .

С учетом ОДЗ х₂ – посторонний корень.

Ответ: 3.

 

3. Решите уравнение:

    .

Решение.

Преобразуем левую часть уравнения:

Показатель степени х есть сумма бесконечно убывающей геометрической прогрессии .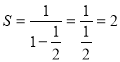

 

Следовательно, имеем уравнение  , откуда  , но ОДЗ , значит

Ответ: 2.

4. Решите уравнение:

.

Решение.

.

Пусть ,  . Тогда .

Данное уравнение примет вид: , ,

. Если у=0, тогда х₁=а; если с=0, тогда х₂=в.

,  или , т.е.

. Откуда находим, что х₃ и х₄ – не действительные корни.

Значит,

Ответ: .

 

5. Решите уравнение:

.

Решение.

 

. Возводя обе части данного уравнения в квадрат и упрощая полученное выражение, имеем уравнение

Равносильное системе: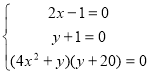, из которой находим: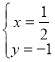

Ответ: .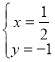

6. Решите уравнение:

    

Решение.

В основе решения данного уравнения лежит метод мажорирования, связанный с применением известных неравенств между средним арифметическим и средним квадратичным двух и трех чисел и . Итак, имеем:

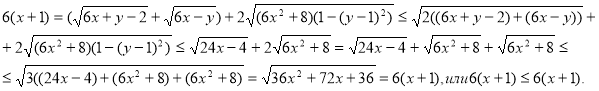
Это означает, что в приведенной выше цепочке неравенств все три знака неравенства следует заменить знаками равенства, то есть должны выполняться три условия, заданные системой:

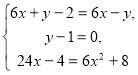      или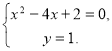 

Значит, 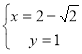  или .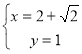

 

Ответ: 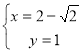   или .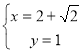

    Задания для самостоятельной работы.

А)   .                                                   Ответ:

Б)                                   Ответ: 7;26.

В)                   Ответ: 31.

Г)                                           Ответ: 3.

Д)                                 Ответ: .

 

Литература

1. Л.Я.Федченко, Г.Н.Литвиненко, В.Н.Швец. Сборник заданий для экзамена по математике. (Алгебра и начала анализа 10-11 класс). Донецк 1997.
2. Сборник задач по математике для поступающих во ВТУЗы. Под ред. М.И. Сканави Москва ”Высшая школа”, 1992.
3. В.С.Кущенко. Сборник конкурсных задач по математике. Ленинград 1963.
4. С.М.Саакян, А.М.Гольдман, Д.В. Денисов. Задачи по алгебре и началам анализа для 10-11 классов. Москва ”Просвещение” 1990.
5. В.Н. Матвеев, Н.М.Матвеев. Сборник задач по математике. Издательство Казанского университета, 1965.
6. В.С.Крамор. Повторяем и систематизируем школьный курс алгебры и начал анализа. Москва ”Просвещение” 1990.
7. Я.Н.Суконник. Математические задачи повышенной трудности. Киев ”Радянська школа”, 1995.
8. Т.П.Савенко, В.Г.Паньков, Ю.Н.Попов. Задачи по алгебре и началам анализа часть 1. Каменец-Подольский ”Абетка-НОВА”, 2004.
9. журнал ”Квант”, 1991, №5.