Методичка "Особистісно орієнтований підхід до процесу навчання математики через впровадження новітніх інноваційних технологій практичного спрямування уроків математики"

Про матеріал

Збірник містить інформаційно-методичні матеріали з актуальних питань щодо підготовки нового покоління до життя в суспільстві, яка здійснюється на основі новітніх технологій, нових підходів до навчання.

Збірник пропонує дидактичні матеріали, що вказують на практичне спрямування уроків математики, стимулюють розвиток творчого потенціалу учнів змістом і засобами математики. Розробки відповідають вимогам навчальних програм, сприяють зміцненню міжпредметних зв'язків, розширюють кругозір учнів.

Перегляд файлу

ВІДДІЛ ОСВІТИ СКОЛІВСЬКОЇ РДА

СКОЛІВСЬКИЙ РАЙОННИЙ МЕТОДИЧНИЙ КАБІНЕТ

Сколівська академічна гімназія

Особистісно орієнтований підхід до процесу навчання математики через впровадження новітніх інноваційних технологій розвивального та практичного спрямування уроків математики

(з досвіду роботи вчителя математики Павлишин Марти Теодорівни)

СКОЛЕ-2017

Інформаційно-методичний збірник.-

СКОЛЕ-2017 - 48 сторінок

Збірник пропонує дидактичні матеріали, що вказують на практичне спрямування уроків математики, стимулюють розвиток творчого потенціалу учнів змістом і засобами математики. Розробки відповідають вимогам навчальних програм, сприяють зміцненню міжпредметних зв’язків, розширюють кругозір учнів.

До видання додаються розробки уроків з математики. Призначено для вчителів математики загальноосвітніх навчальних закладів.

Павлишин Марта Теодорівна, вища категорія, старший вчитель, Сколівська академічна гімназія

$C:\Users\Notbook\Desktop\Марта.tif$

Педагогічне кредо:

Складне зробити простим,

Просте зробити звичним,

Звичне зробити приємним.

В пошуках нових методик

Уміє вчити той, хто вчить цікаво,хто викладає

свій предмет так, щоб у душі учня зазвучали

струни у відповідь і ні на хвилину не засинала

його допитливість.

А.Ейнштейн

Нехай заслужено пишаються своїми відкриттями вчені, нехай гордяться своїми патентами винахідники, нехай не без підстав уважають свою місію особливо вагомою медики, священики, державні діячі, але коли до класу заходить педагог і розпочинається священне дійство, ім'я якому урок, кермо планети й доля людства, його майбутнє - саме в руках учителя.

Професія вчителя є однією з тих дивних професій, де майстер з року в рік продовжує себе в своїх учнях. І немає нічого благороднішого від цієї місії...

Головне завдання вчителя — зробити навчання цікавим. Для учня це — посильним і успішно-результативним, для вчителя — радісним. Найбільша цінність — це особистість дитини, все, що робиться, робиться для неї, для її навчання, виховання, розвитку. А розкрити особистість учня можна, якщо вчитель іде на урок не лише зі знанням навчального матеріалу, методів і прийомів навчання, набором задач і вмінням їх майстерно розв'язувати, але і з різноманітними та цікавими способами організації праці учнів

У сучасному світі бурхливо розвивається бізнес. Він, як відомо, тісно зв'язаний з посиленням логічного мислення, швидкого й правильного прийняття рішень. У школі такі якості виховує математика. Парадоксально, але чомусь ця наука стала менше цікавити дітей. От і доводиться закохувати дітей у королеву наук — математику.

Уроки математики повинні бути насамперед цікавими, збуджувати в учнів прагнення більше знати, розуміти, підвищувати інтерес учнів до математики, глибше засвоювати матеріал, формувати науковий світогляд і критичне мислення.

Пошук і вибір способу побудови уроку потрібно пов'язувати з формуванням умінь учнів спостерігати, аналізувати, узагальнювати, формулювати гіпотези, ставити запитання, висловлювати і відстоювати свої думки, оперувати навчальним матеріалом, а також із розвитком мислення, уваги, уяви, пам'яті учнів, з вихованням пізнавального інтересу, самостійності у здобутті знань, моральності, культури.

Щоб розвивати творчі здібності учнів, їх поступово, але систематично слід залучати до самостійної пізнавальної діяльності. Для забезпечення якісної співпраці між учнями і вчителем традиційного уроку недостатньо.

Нетрадиційний урок — це творча самореалізація вчителя, вияв неповторної його індивідуальності, а для учня — це свято серед традиційних буднів, сприяє розвитку творчих здібностей особистості і застосування технологій інтерактивного навчання.

Використовуючи елементи інтерактивного навчання, створюються умови, за яких кожен відчуває свою успішність, інтелектуальну спроможність.

Щоб забезпечити глибоке засвоєння теми, продуманою, логічно витриманою системою вправ потрібно дати можливість учням відчути необхідність використання набутих знань у процесі розв'язування задач практичного змісту, пропонувати вправи, які вимагають не лише знань, а й певних пошуків, роздумів, логічних міркувань. При цьому широко використовувати теореми та задачі, які можна довести (розв'язати) кількома способами. Для зацікавлення математикою, для розвитку логічного мислення пропонувати також задачі на кмітливість, задачі з помилками в умові, підвищеної складності, розгадувати ребуси, кросворди тощо.

Для успішного формування у школярів рис творчої особистості слід надавати їм максимум можливостей для випробування себе у творчості. Не кожен учень буде в майбутньому математиком, але учні повинні вирости людьми мислячими, всебічно розвиненими, творчими. А найголовніше, щоб на уроках завжди панувала атмосфера довіри, взаєморозуміння, доброзичливості. Сприяє розвитку творчих здібностей учнів і таке завдання, як скласти казку, дійовими особами якої є математичні поняття. Таке завдання є незвичним для уроку математики, тому зацікавлює учнів. І вони пробують писати, хоч і не в усіх це виходить вдало з першого разу. При цьому наголошую, що казка повинна вчити життєвої мудрості.

23 років педагогічної роботи в гімназії, дивовижної, інтенсивної, насиченої радісними емоціями, сумнівами, тривогами, протягом яких я шукаю відповідь на одне питання: яким повинен бути вчитель, якими повинні бути його уроки, щоб діти йшли на них з радістю, щоб на них вони творили, вчилися мислити? Через призму років освітянської праці у мене виробились певні педагогічні аксіоми:

Проблеми звичайного уроку привертають до себе останнім часом пильну увагу. Про них сперечаються на сторінках газет і журналів, їм присвячуються книги. Від школи та від вчителя сьогодення вимагає не тільки дати знання, сформувати програмові вміння та навики в усіх учнів, але головне навчити школярів творчо їх використовувати. Та найчастіше, на жаль, урок математики, як в принципі і будь-який інший урок, проводиться за методикою «роби, як я» (подивись – повтори – запам’ятай).

Школа – найдивовижніша країна, де кожний наступний день не подібний на попередній, де кожна мить – це пошук чогось нового, цікавого, де немає часу сумувати і витрачати час на пусте, де кожний учень – це зодчий майбутнього. Де весь час потрібно поспішати стати цікавим для оточуючих тебе людей, дарувати свою енергію, знання, навики, поспішати відкрити щось нове. І найважливіше в цій країні на ймення школа – вміти дивувати.

Дивлячись на своїх учнів, розумію, що найбільшу радість та задоволення школярі отримують від роботи, яка дозволяє їм відкривати себе: свої можливості, свої здібності. Їх очі загоряються, коли їх вчать чомусь значущому, важливому для життя взагалі, а не для отримання оцінки. Останні роки роботи переконали мене в тому, що не можна іти на урок лише зі знаннями теореми чи добіркою задач.

І єдиним, на мою думку, найефективнішим засобом досягнення мети є інноваційні технології навчання. Інноваційний підхід забезпечує позитивну мотивацію здобуття знань, активне функціонування інтелектуальних і вольових сфер, сприяє розвитку творчої особистості.

Створення ситуації успіху, сприятливих умов для повноцінної діяльності кожної дитини – основна мета, що покладена в основу інноваційних технологій навчання. Багато з них варті уваги сучасного педагога, який прагне дати якісний рівень знань, зробити урок цікавим, досягти максимального взаєморозуміння і співпраці між вчителем і учнем.

Саме тому я працюю на вирішення науково – методичної проблеми: «Впровадження новітніх інноваційних технологій розвивального та практичного спрямування уроків математики».

Актуальність обраної проблеми: розвиток і формування соціально зрілої працелюбної творчої компетентної особистості, яка матиме глибокі знання, а мета моєї роботи як учителя — пробудити учня до творчості, розвинути свідоме ставлення до навчання, прагнення до саморозвитку, самовдосконалення, створити сприятливі умови для виховання й навчання самодостатньої творчої особистості, яка зуміє орієнтуватися на складних життєвих шляхах.

Як відомо, навчання - це двосторонній процес. З одного боку, ефективність навчання визначається тим, наскільки вчитель правильно організує розумову діяльність, використовує можливості пам'яті, допомагає учням опанувати методи пізнання та формує в них навички навчальної діяльності, ураховує вікові й індивідуальні особливості й інше.

З іншого боку, ефективність навчання залежить від активності пізнання та діяльності самого учня. Безумовно, на діяльність учнів великий вплив має особистість учителя, його активність, готовність до навчання. Таким чином, на хід уроку впливають моральні, особистісні особливості вчителя, його емоційний стан, уміння володіти класом тощо. З огляду на все це можна припустити, що в основі будь-якого уроку лежить єдиний процес взаємодії вчителя й учнів.

Прагну, щоб кожен учень, якого я навчаю мав можливість знайти своє місце в житті, і як учень сучасної школи володів такими якостями:

гнучко адаптувався у мінливих життєвих ситуаціях;
самостійно та критично мислив;
умів бачити та формувати проблему (в особистому та професійному плані), знаходив шляхи її раціонального вирішення;
усвідомлював, де і яким чином здобуті знання можуть бути використані в оточуючій його дійсності;
був здатним генерувати нові ідеї, творчо мислити;
грамотно працював з інформацією;
був комунікабельним, умів співпрацювати в колективі;
був конкурентоспроможним у житті;
умів самостійно працювати над розвитком особистої моральності, інтелекту, культурного рівня.

Роль педагога – сприяти розвитку дитини. У своїй роботі намагаюсь дати можливість учневі з будь-яким рівнем навчальних досягнень посильно творити. І допомагають у цьому на уроках завдання, для розв’язку яких потрібно докласти певних зусиль.

Щоб навчити учнів самостійно мислити, викликати віру у власні сили і розум, виховати впевненість у своїх можливостях, необхідно примусити їх пройти через певні труднощі, а не подавати все у готовому вигляді. Через те стараюсь створити проблемні ситуації.

Учень пасивний, коли списує хід розв’язування з дошки, пасивний, коли слухає відповіді товаришів, і навіть питання, адресоване класу, активізує не всіх, а лише тих, чий «темп думання» відповідає темпу фронтального опитування. А пасивність – основний живильний ґрунт нудьги і ліні. Лише активність, лише творчість, лише постійний пошук вирощують справжню людину з гармонійно розвиненим інтелектом.

Чудес в педагогіці не буває. Є велика, важка, часом нестерпно важка, але нескінченно радісна за віддачею робота. Чудово, коли діти чекають урок, коли підбігають і питають: «Що у нас сьогодні буде на уроці?» І кожного дня їх потрібно чимось дивувати.

Вміння зацікавити сучасну молодь своїм предметом, підготувати їх до життя і роботи в сучасному суспільстві, навчити їх використовувати набуті знання, вміння, досвід для свого подальшого становлення і розвитку, на мій погляд, і є педагогічна майстерність, до якої ми всі прагнемо.

Освіта, навчання – це за своєю суттю суперечливі процеси. З одного боку, ці процеси означають примус, підштовхування учня до оволодіння необхідними, чітко визначеними знаннями, вміннями й навичками, без яких неможливо досягти освіченості, компетентності. З іншого – освіта і навчання ґрунтуються на активній діяльності самого учня, самоорганізації його поведінки.

Не можна навчити людину всупереч її волі, тому єдиний вихід для нас, вчителів, – пробудити інтерес до навчання, зацікавити учнів. Підняти кожного учня з категорії людини, яку навчають до категорії колеги по процесу навчання – особистості, яка навчається, набуває досвіду.

У цьому сенсі способи, методи учительського впливу на навчальний процес стають актуальною проблемою.

Процес навчання – це не автоматичне „вкладання” в голову учня навчального матеріалу. Цей процес потребує напруженої розумової праці, особистої активності дитини в ньому. Пояснення і демонстрація самі по собі ніколи не дають справжніх стійких знань.

Часто у роботі вчителі надмірно захоплюються використанням якоїсь однієї педагогічної технології, не помічаючи її «мінусів», не враховуючи індивідуальні особливості своїх учнів, їх готовність до роботи за певною технологією. Експеримент не приносить бажаних результатів, і вчитель розчаровується у всіх нововведеннях, продовжує працювати за «старою системою».

Вважаю, що сучасному педагогові необхідно вибрати те «зерно», що дасть змогу створити свою міні-методику. А у творчого вчителя і учні прагнутимуть до творчості.

У своїй педагогічній практиці апробовую спосіб інтеграції окремих елементів таких сучасних технологій навчання :

• Проектне навчання;

• Інтерактивна технологія;

• Особистісно зорієнтоване навчання.

Для того, щоб така інтеграція принесла бажаний результат, намагаюся вникнути в методику кожної з освітніх технологій і використовувати на своїх уроках залежно від теми, мети виучуваного матеріалу, а також типу уроку та навчального предмета.

Незважаючи на розмаїття нововведень, основною формою організації навчальної діяльності залишається урок. Яким же повинен він бути? Сучасний урок – це урок демократичний. Для такого уроку характерними ознаками є:

• навчання не словом, а справою;

• проведення його не для учнів, а разом з ними;

• спрямовування діяльності не на клас в цілому, а на особистість кожного учня;

• забезпечення повного засвоєння навчального матеріалу на уроці.

Саме уникненню багатьох недоліків у підготовці до уроку допомагає чітке використання методики тієї чи іншої технології, суттєвою особливістю якої є протиставлення довільних дій чіткому алгоритму, системі логічно вмотивованих дій, послідовному переходу від одного елемента до іншого.

Складові ефективності й успішності уроку можна зобразити так:

Взявши за основу створення психологічного комфорту та активну взаємодію в процесі навчання, керуюся такими принципами:

головним є не предмет, якому я навчаю, а особистість, яку формую;
кожна людина знайде своє місце в житті, якщо навчиться всьому, що необхідно для реалізації її планів;
кожна думка, висловлена учнем, має право на існування й варта уваги.

Ідеал сучасного навчання – особистість із гнучким розумом, зі швидкою реакцією на все нове, з ідеальними комунікативними здібностями. Тому вважаю, що такі форми роботи, як рольові ігри, словесне малювання, розвиток логічного мислення, дослідницька діяльність, захист проектів, представлення презентацій сприяють загальному розвитку учнів. На мою думку, види уроків, які я впроваджую у своїй роботі, допомагають відійти від стандарту, підштовхнути учня до власного, неповторного, індивідуального, особливого погляду на життя. Це, як правило,

уроки - відкриття,

уроки – дослідження,

уроки – подорожі,

уроки – практикуми.

На таких уроках створюється ситуація довіри та успіху, і за таких обставин дитина розкривається, може повірити у свої можливості, реалізуватися як творча особистість, сміливо продемонструвати свої здібності.

І як результат: учень-випускник не тільки володіє знаннями, уміннями та навичками з предмета, але й уміє формулювати власну точку зору, відстоювати свою позицію, співпрацювати в групі, колективі, мати коло однодумців, бути комунікабельною, толерантною особистістю.

Ретельно готуюсь до кожного уроку, продумуючи хід заняття, добираючи ефективні методи та прийоми. Допомагають у цьому сучасні технології.

Так, новий матеріал я подаю дітям у вигляді блок-схем, таблиць, малюнків, пірамід і т.п. До того ж, часто використовую власні мультимедійні презентації на уроках. Це викликає живий інтерес в учнів, покращує процес засвоєння матеріалу, унаочнює пізнання, сприяє розвитку творчих здібностей. Мною створена низка інформаційних презентацій вчителя до різних тем ..

Будь-яка творчість передбачає любов, тому і діяльність учителя немислима без неї. Якщо учень і вчитель ідуть на урок з почуттям любові, добра, поваги, то відбудеться єднання душ, що сприятиме ефективному навчанню й вихованню. Саме з любові і поваги проростає коріння взаєморозуміння, взаємозбагачення, взаємодопомоги, взаємодовіри, взаємоконтролю.

Доброзичливе, щире, відкрите, емоційне, наукове спілкування – ось що таке для мене уроки математики. На них учень і вчитель обмінюються враженнями, сперечаються, висловлюють свої думки, пізнають щось нове. Найкорисніші уроки, які наповнені добрими емоціями і почуттям, на яких панує робоча атмосфера. Якщо ви зайшли до класу, а очі учнів мертві, ледь жевріють, спробуйте своїм поглядом, словом «запалити» їх, тому що без цього ваш урок пройде марно.

Нетрадиційний, нестандартний урок!... Цього можна досягти лише за допомогою нових технологій навчання, в процесі яких учні залучаються до пізнавально-навчальної діяльності. До таких технологій належать інтерактивні, проектні, інформаційні, модульно-розвивальні тощо.

Впровадження ідеї покращує рівень викладання з математики, оскільки введення нових технологій вносить радикальні зміни у процес: кожен учень має можливість навчатися у відповідному для нього темпі і на тому рівні, який відповідає його здібностям. Таким чином, можна виділити переваги застосування інноваційних технологій. Вони допомагають навчити учнів активним способам отримання нових знань; дають можливість опанувати більш високим рівнем особистої соціальної активності; створюють такі умови в навчанні, при яких учні не можуть не навчитися; стимулюють творчі здібності учнів; допомагають наблизити навчання до практики повсякденного життя, формують не тільки знання, вміння та навички з предмета, а й активну життєву позицію. Створюється ситуація успіху.

І. Інтерактивні технології

Як навчити учнів математики? Як розвинути логічне мислення? Як активізувати пам’ять, увагу? Як підвищити інтерес до знань? Як зацікавити процесом навчання?

Відповіді на ці запитання дають сучасні технології навчання, зокрема інтерактивні.

Слово „інтерактив” походить від англійських слів „inter” - взаємний та „act” – діяти. Таким чином, інтерактивний – здатний до діалогу, взаємодії. Інтерактивне навчання – це спеціальна форма організації пізнавальної діяльності, спрямована на створення комфортних умов навчання, за яких кожен учень відчуває свою успішність, інтелектуальну спроможність.

Сутність інтерактивного навчання полягає в тому, що вчитель організовує пізнавальну діяльність учня таким чином, що він самостійно розв’язує певні ситуації, проблеми, спираючись на свої потенційні можливості і вже набуті знання в процесі взаємодії „учень – інформація”, „учень – ситуація”, „учень – проблема”, „учень – учень”, „учень – група”, „учень – вчитель” тощо.

Навчальний процес організований так, що всіх учасників залучено до процесу пізнання, формування висновків, створення певного результату, де кожен робить індивідуальний внесок, обмінюється знаннями, ідеями, способами діяльності. Відбувається цей процес в атмосфері доброзичливості та взаємопідтримки. Це дозволяє не тільки отримати нові знання, а й розвиває пізнавальну діяльність, переводить її в більш високі форми кооперації та співробітництва.

Інтерактивне навчання дозволяє розв'язати одразу кілька завдань: розвиває комунікативні вміння й навички, допомагає встановленню емоційних контактів між учасниками процесу, забезпечує виховне завдання, оскільки змушує працювати в команді, прислухатися до думки кожного. Використання інтерактиву знімає нервове напруження, дає можливість змінювати форми діяльності, переключати увагу на основні питання.

II. Інформаційні технології

У зв’язку із активним розвитком інформаційних технологій та їх впровадженням в різні сфери повсякденного життя перед освітянами виникає питання щодо включення їх до переліку педагогічних інновацій.

Інформаційні технології – це потужний інструмент для здобуття дитиною найрізноманітнішої інформації, це ефективний засіб для підвищення інтересу до навчання.

При використанні інформаційних та комп’ютерних технологій найбільш привабливою є можливість використання комп’ютера з метою конструювання середовища навчання не з точки зору тих розв’язань, які нав’язує сам комп’ютер, а в руслі тих методичних та дидактичних завдань, які вчитель ставить перед собою.

Комп’ютеризація навчально-виховного процесу, яка відповідає змісту шкільної програми, орієнтована на розливальну функцію шкільної освіти та її гуманізацію, дає можливість для творчого розвитку дітей та вчителів, змогу звільнитися від нудного традиційного навчання та розробляти нові ідеї, розв’язувати більш цікаві та складні проблеми.

З появою комп’ютера в освіті народжується нове інформаційне поле – поле програмних продуктів навчального призначення. Однією з навчальних дисциплін, де найбільш вдало використовується комп’ютер, є математика.

Окрім використання спеціально створених програм навчального призначення для вивчення окремих розділів та тем з математики (пакет програм „GRAN”, „DG” (динамічна геометрія), програмно-методичний комплекс „TepM” (система комп’ютерної алгебри), програма „ADVANSED GRAPHER” (для побудови графіків функцій)), комп’ютер широко використовується для реалізації описаних вище методів та прийомів інтерактивних технологій, таких як „метод проектів”, „метод презентацій”, „метод реклами”, для чого стають у пригоді системи комп’ютерних презентацій, системи створення слайд-шоу, кліпів, відео.

Важливим етапом у вивченні математики є контроль навчальних досягнень учнів. Останнім часом він часто здійснюється шляхом методу тестування, який є зручною, ефективною, швидкою формою проведення перевірки знань, умінь та навичок учнів. Ще більш ефективним (запобігання списуванню) та швидким (миттєве оцінювання) стає цей процес, якщо використовувати різноманітні системи комп’ютерного тестування.

Прикладний програмний засіб ЕТ „Microsoft Excel” допоможе складати таблиці значень функцій, будувати графіки, діаграми, знаходити найбільше та найменше значення функції, обчислювати середнє арифметичне тощо.

Звичайно, вчитель має знайти „золоту середину” між повною автоматизацією навчального процесу та кропіткою роботою учня над отриманням ходу розв’язування математичної задачі аби, навчаючи за допомогою комп’ютерних технологій, не нашкодити процесу розвитку мислення, уяви, логіки.

Від теорії до практики

Для нашої освіти характерна інертність: з великим запізненням вона реагує на потреби суспільства, що динамічно змінюються. Під час радикальних змін інертність реагування має негативне значення. В цьому плані застосування інноваційних технологій є найбільш ефективним. Ми завжди повинні пам’ятати, що тільки через самодіяльність можна знайти своє місце в складному, багатогранному суспільстві. Навчання шляхом сучасних інноваційних технологій – це шлях особистісного розвитку, оскільки саме такий шлях стає основою для самостійного істинного існування.

Кожен учитель – і професіонал, і початківець, прагнучи іти в ногу з життям, а не рухатись за інерцією, повинен, принаймні, спробувати підготувати і провести урок за новою технологією. Та, впевнена, побачивши результат і реакцію учнів, уже не матиме права нехтувати цими інноваціями.

Подані нижче розробки уроків показують застосування різних форм, прийомів, методів описаних вище технологій. Тут переплітаються різні технології, десь відповідають теоретичному тлумаченню, а десь видозмінені, в чомусь актуальні, а в іншому, можливо, недоречні. Та ці уроки - продукт моєї праці, творчості, мого досвіду, а головне – вони були проведені і сподобались учням. Тому пропоную їх Вашій увазі, може, вони сподобаються і Вашим учням. В організації та проведенні моїх уроків лежить системний підхід, основою якого є відомий логічний ланцюг:

Мета

Засоби

Результат

І. Дидактичні цікавинки

Люди відрізняються один від одного за своїми здібностями, через що вони по-різному виконують різні роботи. І якщо час вимагає, щоб кожна людина розкрила свої творчі можливості, то працювати з усіма учнями однаково — неприпустимо. Кожен учень може і повинен зробити стільки кроків до мети, на скільки він здатний. Ніхто не повинен стояти на місці.

У процесі навчання намагаюся більше уваги звертати на учнів, які вимагають особливої допомоги та більшої кількості вказівок. Цих учнів частіше викликаю до дошки. Крім того, пропоную їм картки із завданнями, до яких вказано план або подано зразок розв'язування. Це допомагає дитині і спрямовує її діяльність. Іноді на таких картках подані розв'язання завдань з деякими пропусками.

Картки з пропусками

1. Обчислити:

2. Знайти х, якщо 12 : 8 = х : 10.

Розв'язання: За основною властивістю пропорції

8•х = 12•…,

8х = 120,

х = 120 : …,

х = Відповідь. х = 15.

Дитяче захоплення розфарбовуванням я ефективно використовую на уроках математики під час вивчення нового матеріалу, для закріплення певних навичок та в процесі розв'язування задач.

Наприклад, коли учні 5-го класу ознайомлюються з поняттям променя, можна запропонувати їм таке завдання: «Точка розбиває пряму на два промені. Розфарбуйте їх у різні кольори». Дитині легше буде показати ці промені.

Під час розв'язування задач на знаходження площ фігур складної форми п'ятикласникам пропоную розбити фігуру на такі, площу яких вони можуть знайти. Кожну фігуру слід виділити окремим кольором кольоровою крейдою; доцільно розглянути різні способи розбиття і обрати найзручніший.

Коли вводиться поняття від'ємних чисел на координатній прямій у 6-му класі, доцільно частину прямої, на якій зображено додатні числа, виділити одним кольором, а частину прямої, де зображено від'ємні числа, — іншим. Таку пряму можна розглядати і у вертикальному розміщенні, тоді учні легше сприймають поняття осі Оу з напрямом «угору — вниз».

У процесі вивчення координатної площини колір можна використати так: частини осі Ох та осі Оу, де зображені від'ємні числа, виділити одним кольором, а частини осі Ох та осі Оу, де зображені додатні числа, - іншим.

При такій методиці працюватиме зорова пам'ять учнів, що дуже важливо для засвоєння будь-якого матеріалу. Це допомагає шестикласнику під час відпрацювання навичок відшукання точок на координатній площині за їх координатами.

Можна використати колір і на уроках алгебри. Коли вивчається винесення спільного множника за дужки, я виділяю кольором цей множник. Потім записую його перед дужками, а в дужках — все, що не виділено кольором. Наприклад,

3х + 3у = 3(х + у),

15ху + 20у = 5•Зху+5•4у=5•у(3х + 4).

Аналогічно і під час розкриття дужок. Якщо перед дужками стоїть виділений кольором множник, то хіба можна не з'єднати його з кожним доданком у дужках стрілочкою, щоб потім парами виписати їх зі своїми знаками?

Наприклад,

15(а + b)=15a + 15b

Таким чином, ризик помилки значно зменшується, а навички поступово закріплюються.

На уроках геометрії в 7-му класі під час вивчення поняття суміжних кутів корисно сторони одного кута виділити одним кольором, а сторони другого — іншим. Тоді спільна сторона суміжних кутів буде виділена двома кольорами, оскільки вона належить кожному куту. Таку методику застосовую під час вивчення вертикальних кутів і ознак рівності трикутників. Виділені кольором елементи легше показати на малюнку, а отже, і запам'ятати. Колір я використовую на перших уроках засвоєння нового матеріалу, а з набуттям навичок потреба в ньому поступово зменшується. Учні виконують завдання правильно без допоміжного розфарбовування.

Роботу з формування у школярів умінь подавати многочлен у вигляді добутку множників способом групування я організовую так. Учням роздаю картки, які містять поетапний зразок виконання завдання.

Картка-зразок

bx+cx+by+cy=

= (bx+by)+(cx+cy)=

=b(x+y)+c(x+y)=

= (x+y)(b+c).

Перший крок

Другий крок

Третій крок

Тоді

bx +cx + by + cy = (x + y) (b + c).

Після цього пропоную учням аналогічні завдання.

Розкласти на множники:

а) ах + ау + 2х + 2у =

перший крок.................................

другий крок...................................

третій крок....................................

б) 7p + 7k + cp + ck =

в) ab + ac – b – c =

На початковому етапі засвоєння формул скороченого множення, наприклад під час перетворення виразу (4+р) , сприяє формуванню в учнів кращих умінь така символічна наочність:

4 p 4 4 p p

Для набуття умінь виносити спільний множник за дужки корисною буде наочність.

У своїй роботі я застосовую подвійні правила, які дають можливість сприймати їх не тільки на слух, а й залучити зір для виділення спільних та відмінних властивостей у формулюванні, побачити аналогії, більш глибокі зв'язки, полегшують запам'ятовування. Наприклад:

Косинусом/синусом гострого кута прямокутного трикутника називається відношення прилеглого/протилежного катета до гіпотенузи.

Діагоналі прямокутника/квадрата рівні.

Щоб діти вчилися аналізувати свою самостійну роботу, я практикую не виправляти допущені помилки, а лише вказати на них (підкреслюю); в кінці роботи можу вказати також, який матеріал необхідно учневі повторити. Це дає йому змогу самостійно знайти правильну відповідь.

Враховуючи різні типи розумової діяльності учнів, я часто пропоную для них одне й те саме завдання, але з різною умовою виконання.

Наприклад:

1. Обчислити:

2. Розставити дужки так, щоб отримати правильну рівність:

Перше завдання я пропоную учням з лінійним синтетичним типом мислення, а друге з успіхом розв'яжуть нелінійні аналітики.

Діти відрізняються не лише типом мислення, а й характером сприймання навчальної інформації, типом спілкування і за багатьма іншими параметрами.

Щодо різних типів сприймання матеріалу, здійснити перевірку одного вміння можна так:

1. Аудіальний тип (обов'язково прочитати вголос).

Знайти число, якщо 2,5 становлять 5/7 від нього.

2. Візуальний тип.

Знайти число за схемою:

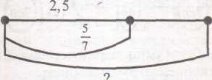
3. Кінестетичний тип.

Побудувати відрізок, якщо даний відрізок АВ становить від нього 5/7.

А В

Як засіб організації самоконтролю використовую аркуші «Рефлексії».

Наприклад, в аркуші «Рефлексія» передбачаю, що учень на певному етапі уроку повинен відповісти для себе на запитання:

а) Як я володію матеріалом (зовсім не володію, володію повністю)?

б) Як я розумію завдання (не розумію взагалі, усі завдання розумію)?

Під час вивчення математики учні не завжди бачать зв'язок між елементами (величинами), що вивчаються, а іноді не можуть пов'язати між собою окремі теми. Опорні конспекти допомагають подолати це.

Під опорним конспектом учні розуміють схеми, які відображають зміст і структуру матеріалу, що вивчається. Опорний конспект дає змогу виділити основні твердження та означення і допомагає запам'ятати їх. Основна мета використання опорних конспектів:

• навчити учнів аналізувати теоретичний матеріал і виділяти основне;

• полегшити вивчення означень і тверджень.

У процесі навчання опорні конспекти будую під час пояснення нового матеріалу. Розглядаючи нове означення чи твердження, аналізуючи його, записую опорний конспект на дошці. Учні записують його в зошити і мають змогу відразу з'ясовувати незрозумілі моменти.

Опорні конспекти можуть бути різними. Найпростішим є лінійний опорний конспект. У твердженні, що вивчається, виділяю основні особливості, які послідовно зв'язані одна з одною. Наприклад:

Пропорція

→

рівність

→

двох відношень

→

а:b = c:d

Або

а/b = c/d

Деякі твердження описати так не можна, оскільки поняття має кілька особливостей. У такому випадку використовую розгалужений опорний конспект. Розглядаючи кожний випадок, поступово записуємо його: вчитель на дошці, а учні — в зошитах. Розгалуження в конспекті дає змогу учням усвідомити зв'язки між усіма частинами твердження.

Наприклад:

Частка двох чисел	→	з однаковими знаками	→	є число додатне

	→	з різними	→	є число
		Знаками		від'ємне

У процесі розв’язування вправ я також виділяю основні етапи і записую їх за допомогою опорного конспекту. Він має іншу форму запису (див. табл.)

Таблиця

	Розв'язати рівняння	-2(х+5) + 3 =
		= 2-6(х+1)
1	Якщо в рівнянні є	-2х-10 + 3 =
	дужки, розкриваємо їх	= 2-6х-6
2	Переносимо	-2х + 6х =
	доданки, які містять	= 10-3 + 2-6
	невідоме, в ліву
	частину, а решту
	доданків - у праву,
	змінивши при цьому
	знаки на протилежні
3	Зводимо подібні	4х = 3
	доданки
4	Знаходимо корінь	х = 3 :4
	рівняння	х = ¾
		Відповідь. х = 3/4

Наступні рівняння діти розв'язують у зошитах, на дошці опорний конспект залишається. Розв'язання рівняння учні записують на дошці в правій частині, виконуючи кожний пункт, записаний у лівій частині.

Опорні конспекти діти використовують також і для перевірки своїх знань. Ними зручно користуватися в процесі повторення матеріалу. Опорні конспекти використовуються в комплексі з іншими засобами навчання.

Ведучи пошуки нових методів, прийомів і форм роботи, вдосконалюю добре відоме, вносячи елементи новизни.

ІІ.Конспекти відкритих уроків

ТЕМА УРОКУ: Квадратична функція.

МЕТА УРОКУ: Повторити, узагальнити і систематизувати знання учнів з теми «Квадратична функція» , удосконалити практичні навички їх застосування для розв’язування завдань та побудови графіків на координатній площині та за допомогою комп’ютера, виявити рівень навченості учнів з даної теми та усувати прогалини в знаннях, створити умови для підготовки учнів до підсумкової контрольної роботи. Формувати потребу та вміння здобувати та упорядковувати з різних джерел інформацію до даної теми. Виховувати впевненість у своїх силах, почуття відповідальності.

ТИП УРОКУ: Урок подорож - урок узагальнення та систематизації з використанням ІКТ.

ОБЛАДНАННЯ: Підручник для 9 кл (А.Г.Мерзляк, Алгебра), комп’ютери, диски - презентацій, роздатковий матеріал, комп’ютерний супровід уроку (слайди), ППЗ Microsoft Excel, Advanced Grapher, картки для практичної роботи з ППЗ, креслярські прилади, шаблони парабол.

ОЧІКУВАНІ РЕЗУЛЬТАТИ:

Учні знають: 1. Теоретичний матеріал з даної теми, зокрема, визначення функції, її графік та властивості.

2. Сфери застосування квадратичної функції.

3. Історію дослідження даної теми.

Учні вміють: 1. Будувати графіки квадратичної функції.

2. Здійснювати перетворення графіків функцій.

3. Застосовувати властивості функцій для розв’язування завдань.

КОМПЕТЕНТНОСТІ: соціальна,комунікативна,інформаційна, самоосвіти.

ЕПІГРАФ:

«Найвище призначення математики полягає в тому, щоб знаходити потаємний порядок у хаосі, який нас оточує».

Роберт Вінер

«Графік – це лінія, що говорить, яка може багато про що розповісти» М.Б.Балк

ХІД УРОКУ:

І.Організаційний момент уроку.

ІІ. Мотивація навчання.

Що, на Вашу думку, легше сприймається в оточуючому нас світі? Речі упорядковані чи хаотичні?

Ну звичайно – упорядковані ! Тому, «Найвище призначення математики полягає в тому, щоб знаходити потаємний порядок

у хаосі, який нас оточує». Роберт Вінер

Недарма ці слова стали епіграфом даного уроку. Пам’ятаймо: хто краще у житті зможе структуризувати свої ідеї, плани, наміри, той

знайде шляхи для їх реалізації.

Сьогодні наш урок побудований, як подорож країною «Квадратична функція». Бажаю всім приємних вражень від цієї мандрівки.

Наша подорож матиме такий маршрут ( станції демонструються на слайдах):

МАРШРУТ ПОДОРОЖІ:

* ІСТОРИЧНА *ТЕОРЕТИЧНА *ПОШУКОВО-ДОСЛІДНИЦЬКА

* ДІАГНОСТИЧНА *ПЕРЕВІРОЧНА

*ПРАКТИЧНА *ХВИЛИНКА-ЦІКАВИНКА.

У кожного з Вас на столі є пам’ятка, ознайомтеся з нею та залишіть перед собою.

« Пам’ятка учасника подорожі »

Під час подорожі будь зібраним і дуже уважним .

Працюй швидко , правильно , раціонально використовуючи час .

НЕ МОЖНА

1.Викрикувати відповіді або запитання, підказувати .

2. Порушувати дисципліну на уроці й правила гри ДЕВІЗ

Вмій кмітливо все збагнути ,

Першим в відповіді бути .

Вчитель. Вирушаймо всі у путь –

Нас цікаві речі ждуть .

ІІІ. Проектна робота.

Вдома Ви самостійно готували інформацію до даної теми.

Отож, ознайомимось з проектами:

Станція * ІСТОРИЧНА

(Звіт групи істориків відбувається у формі повідомлень з демонстрацією відповідних слайдів).

Станція *ТЕОРЕТИЧНА

(Звіт групи теоретиків дають означення квадратичної функції, з’ясовують її властивості та розповідають про перетворення графіків функції).

Станція *ПОШУКОВО-ДОСЛІДНИЦЬКА (Звіт групи дослідників, розповіді з презентаціями про застосування параболи у житті).

Станція * ДІАГНОСТИЧНА

Свої здібності людина може спізнати, тільки спробувавши застосувати їх на ділі.

Луцій Анней Сенека

ІV. Актуалізація опорних знань учнів.

Фронтальне опитування ( слайдова презентація)

Доповніть твердження:

1) Квадратичною функцією називається функція , яку можна задати формулою ...

2) Графіком квадратичної функції є...

До речі, недарма кажуть, що

«Графік – це лінія, що говорить, яка може багато про що розповісти» М.Б.Балк

3) Графік квадратичної функції у = ах² + bx + c симетричний відносно прямої...

4) Вітки параболи напрямленні вгору , якщо ...
5) Абсцису вершини параболи можна знайти за формулою ...

6) Значення Х , при яких значення функції дорівнює нулю , називаються ...

7) Область визначення параболи - ...
8) Область значень : якщо а > 0 , то ... ;
якщо a < 0 , то ... .

9) Оберіть із заданих функцій квадратичну:

10) Встановіть відповідність між функціями і графіками.

11) Який з даних рисунків є графіком квадратичної функції?

12) Пояснити побудову графіків даних функцій:

13) Встановіть відповідність ...

14) Назвіть координати вершини параболи та вкажіть напрямок гілок:

15) Назвіть рівняння параболи у вигляді у = а(х + m)² +n, якщо відомо, що вона отримана:

з параболи у = х² паралельним перенесенням вздовж осі х на 5 одиниць ліворуч та вздовж осі у на 3 одиниці вниз;

з параболы у = 2х² паралельним перенесенням вздовж осі у на 6 одиниць вгору та вздовж осі х на 1 одиницю праворуч;

из параболы у = - 5х² паралельним перенесенням вздовж осі х на 4 одиниці ліворуч та вздовж осі у на 4 одиниці вгору

Станція *ПЕРЕВІРОЧНА

V. Перевірка засвоєння знань і навичок учнів, здобутих на попередніх уроках.

Самостійна робота ( 5 хвилин)

Учитель. У кожного з вас на столі лежать червоні і зелені трикутники . Візьміть , будь ласка , по одному трикутнику . Хто взяв червоний трикутник , працює над тестовим завданням за комп’ютером, а ті, хто вибрав зелений трикутник, працюватимуть на карточках, розв’язуючи завдання в тестовій формі „Перевір себе”, сторінка 116 підручника.

Станція *ПРАКТИЧНА

VІ. Закріплення навичок та вмінь побудови графіків квадратичної функції і використання її властивостей при розв’язуанні вправ.

Робота в парах

1. На партах лежать файли з завданням та листи з координатною площиною.

Частина учнів за допомогою шаблона функції у=х2 , а інші на комп’ютері в одній системі координат схематично будують графіки функцій:

у = -х2 + 2;

у = х2 – 3;

у = (х – 1) 2;

у = -(х + 2) 2;

у = (х + 1) 2 – 2;

у = -(х – 2) 2 + 1;

у = (х + 3)*(х – 3);

у = х2 + 4х – 4;

у = х2 – 6х + 11;

10)у = х2 – 6х + 9.

Для кожного випадку записати область значень і проміжки зростання та спадання.

Після закінчення роботи, порівнюються результати.

Робиться висновок, що правила перетворень дійсні для будь яких графіків.

Станція *ХВИЛИНКА-ЦІКАВИНКА

Розгадати математичний термін

На чому будується система координат ?

Вісь ОХ ще називають віссю …

Число, яке задовільняє рівняння називається його …

Як називається перша координата точки ?

Якою крейдою найчастіше працюємо на дошці ?

Як ще називають вісь ОУ ?

Функція виду у=кх+b

План розв’язку...

П	лощині
А	бсцис
Р	озв’язком
А	бсциса
Б	ілою
О	Рдинат
Л	Інійна
а	Лгоритм

VІІ. Підведення підсумку уроку.

Ось і закінчилась наша подорож до країни «Квадратична функція» . Зверніть, будь ласка, увагу на маленький файл у Вас на столах: у ньому лежать пелюстки квітів, жовтого та червоного кольору.

На жовтій пелюстці запишіть, про що ви дізналися на цьому уроці , а на червоній – що Вас особливо здивувало у час вивчення теми.

А тепер представників груп я запрошую прикріпити пелюстки квітів з вашими записами до нашої квітки. Ваші записи ми проаналізуємо на наступному уроці.

VІІІ. Завдання додому.

Повторити параграф 2, п. 7-11 підручника, стор.59-109.

Розв’язати № 355, 361, 376 .

Додатково № 380.

За бажанням удома пропонується виконати творче завдання: підготувати презентацію побудови графіків функцій з модулем.А також Ви зможете переглянути в інтернеті фільм Ольги Стоцької, що називається «Ода параболі». Якщо вам сподобався цей фільм і вам хочеться виразити свої емоції з приводу математики – «Цариці наук», то ви теж можете попробувати свої сили у виготовленні таких фільмів.

Вчитель: Властивості параболи широко застосовуються в природі, будівництві та архітектурі. Доторкнемось серцем і душею до святинь рідної землі і ще раз пересвідчимось, що наші далекі предки добре знали математику. До Вашої уваги відеоролик « СІМ ЧУДЕС УКРАЇНИ ».

Додаткові завдання:

1. Побудуйте графік функції і опишіть його властивості.

2. Побудувати графік функції

3. Побудувати графік функції

ТЕМА УРОКУ: Декартова система

координат

МЕТА УРОКУ: Повторити, узагальнити і систематизувати знання учнів з теми «Декартова система координат», удосконалити практичні навички їх застосування для розв’язування задач та побудови малюнків за заданими координатами на координатній площині за допомогою комп’ютера, виявити рівень навченості учнів з даної теми та усувати прогалини в знаннях, створити умови для розкриття багатогранності зв’язків математики з практичною діяльністю людини. Формувати потребу та вміння здобувати та упорядковувати з різних джерел інформацію до даної теми. Виховувати впевненість у своїх силах, почуття відповідальності. Розвивати здібності учнів, творчу активність, ініціативу, правильність і чіткість мови, виховувати почуття колективізму, взаємодопомоги..

ТИП УРОКУ: Урок проектного навчання – історичний екскурс – урок узагальнення та систематизації з використанням ІКТ.

ОБЛАДНАННЯ: Підручник для 9 класу (А.Г.Мерзляк, Геометрія), комп’ютери, мультимедійна презентація, роздатковий матеріал, Microsoft Excel, Advanced Grapher, картки для практичної роботи з ППЗ Risuem.rar, креслярські прилади.

ОЧІКУВАНІ РЕЗУЛЬТАТИ:

Учні знають: 1. Теоретичний матеріал з даної теми, зокрема, формули координат середини відрізка, формули відстані між двома точками.

2. Сфери застосування координатної площини.

3. Історію дослідження даної теми.

Учні вміють: 1. Застосовувати формули відстані між двома точками та

координат середини відрізка до розв'язування задач.

2. Будувати малюнки за заданими координатами.

3. Використовувати отримані знання на практиці і в

повсякденному житті.

КОМПЕТЕНТНОСТІ: соціальна,комунікативна,інформаційна, самоосвіти.

ЕПІГРАФ: Мало мати хороший розум,

головне – добре його застосовувати.

Рене Декарт

Під час роботи над проектом утворені групи: Історики. Теоретики-науковці. Пошуківці-дослідники. Винахідники-експериментатори. Літератори-практики.

ХІД УРОКУ:

І.Організаційний момент уроку.

ІІ. Мотивація навчання.

Відомий французький письменник ХІХ ст.. Анатоль Франс одного разу зауважив: «Навчатися можна тільки весело… Щоб перетравлювати знання, потрібно поглинати їх з апетитом.» Тому сьогодні на уроці ми не просто будемо повторювати вивчений матеріал, але й, сподіваюсь, цікаво проведемо час. Нас чекає багато роботи, але це не має завадити нашому гарному настрою.

На кожному столі лежить персональна картка обліку виконання завдань проекту, у яку внесені певні бали і упродовж уроку будуть додані ще додаткові бали за роботу. Бажаю Вам накопичити достатню кількість балів, щоб у кінці виконання проекту претендувати на високу оцінку!

Для розминки проведемо гру «Мікрофон».

Завдання: запропонуйте свій варіант відповіді для незакінченого речення

« Не існує не талановитих людей,а є ті…».

(Відповідь:…які займаються не своєю справою)

Можливо, цей урок геометрії стане тією справою, яка дасть змогу кожному з вас розкрити свої таланти. Будьте активними, наполегливими, кмітливими!

Пам’ятаймо: хто краще у житті зможе структуризувати свої ідеї, плани, наміри, той обов’язково знайде шляхи для їх реалізації.

ІІІ. Проектна робота.

Сьогодні наш урок побудований, як подорож країною «Декартова система координат». Бажаю всім приємних вражень від цієї мандрівки, яка матиме такий маршрут ( станції демонструються на слайдах):

МАРШРУТ ПОДОРОЖІ:

* ІСТОРИЧНА

*ТЕОРЕТИЧНА

*ЛІТЕРАТУРНА

*ПОШУКОВО-ДОСЛІДНИЦЬКА

* ДІАГНОСТИЧНА

*ПЕРЕВІРОЧНА

*ТВОЧО-ПРАКТИЧНА

У кожного з Вас на столі є пам’ятка, з якою Ви вже знайомі. Нехай вона буде Вашим орієнтиром під час нашої мандрівки

« Пам’ятка учасника подорожі »

Під час подорожі будь зібраним і дуже уважним .

Працюй швидко , правильно , раціонально використовуючи час .

НЕ МОЖНА

1.Викрикувати відповіді або запитання, підказувати .

2. Порушувати дисципліну на уроці й правила гри

Вмій кмітливо все збагнути ,

Першим в відповіді бути .

Використовуючи смартфон, зайдіть на сайт LearningApps.org, який є онлайновим сервісом, що дозволяє виконувати інтерактивні вправи, за допомогою яких цікаво вивчати математику за таким посиланням на адресу сторінки http://learningapps.org/892960 . завдання щоб відкрити портрет

Звучить відеоепіграф до уроку від відомого математика Рене Декарта (http://mymathworld4.blogspot.com/p/blog-page_9.html)

Мало мати хороший розум,

головне – добре його застосовувати.

Упродовж певного періоду Ви працювали над проектом «Чарівний світ координат», виконуючи випереджальне завдання. І сьогодні Тім-лідери кожної групи представлять свої дослідження.

Станція * ІСТОРИЧНА

(Звіт групи істориків відбувається у формі повідомлення з демонстрацією відповідних слайдів).

Станція *ТЕОРЕТИЧНА та станція *ЛІТЕРАТУРНА

(Звіт групи теоретиків у вигляді складеного та оформленого кросворду).

Станція *ПОШУКОВО-ДОСЛІДНИЦЬКА

(Звіт групи винахідників-експериментаторів та дослідників, розповіді з презентаціями про застосування координат у житті людини та презентують роботи «Світ навколо нас» (малюнки в координатах) і макети координатних площин).

Станція * ДІАГНОСТИЧНА

А тепер перевіримо на скільки добре ви засвоїли даний матеріал.

ІV. Актуалізація опорних знань учнів.

Фронтальне опитування ( слайдова презентація)

Як називають дві взаємноперпендикулярні координатні прямі, які перетинаються в початку відліку ?

Як називають площину, на якій задано систему координат?

Як називають координатну пряму, яку проводять горизонтально? вертикально?

Яку координату точки ставлять на перше місце, а яку — на друге?

Де містяться точки, ординати яких дорівнюють нулю?

Де містяться точки, абсциси яких дорівнюють нулю?

Як знайти координати середини відрізка, якщо відомі координати його кінців?

Як знайти довжину відрізка, якщо відомі координати його кінців?

Усні вправи

Прочитати запис.

Які координати має точка за знаком у кожній чверті?

Яке з наведених тверджень не правильне?

Знайдіть координати точки на рисунку.

Чи правильно заповнена таблиця?

Знайди помилки!

Знайдіть координати середини відрізка ВС, якщо В(5;4), С(3;2)?

Знайдіть відстань від точки А(-3;4) до початку координат.

Письмові вправи

Вершинами трикутника є точки А(-1;3), В(5;9), С(6;2). Доведіть, що цей трикутник рівнобедрений.

Дано координати вершин трикутника ABC: A(2; -1), В(1; 2), С(-3; 6). Знайдіть довжину медіани трикутника ABC, проведеної з вершини А.

Молодці всі ті , хто добре справився із даним завданням .

Станція *ПЕРЕВІРОЧНА

V. Перевірка засвоєння знань і навичок учнів, здобутих на попередніх уроках.

Самостійна робота ( 5 хвилин)

Учитель. У кожного з вас на столі лежать червоні і зелені трикутники . Візьміть , будь ласка , по одному трикутнику . Хто взяв червоний трикутник , працює над тестовим завданням за комп’ютером, а ті, хто вибрав зелений трикутник, працюватимуть на карточках, розв’язуючи завдання в тестовій формі «Перевір себе», сторінка 116 підручника.

Правильні варіанти відповідей.

Станція *ТВОРЧО-ПРАКТИЧНА

Сестри Абсциса і Ордината до Вас завітали, пропонуючи невелике випробування - виконати на комп’ютері цікаве завдання.

Робота в парах

Учні сідають по двоє за комп'ютер. Виконується робота за індивідуальними картками (Додаток), на яких зазначені координати точок. Їх треба з'єднати послідовно.

7. Станція *ХВИЛИНКА-ЦІКАВИНКА

VІІ. Підведення підсумку уроку.

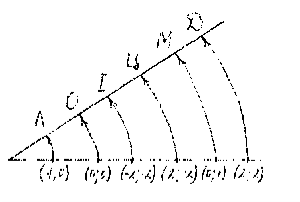Скласти слово, кожна буква якого відповідає певним координатам

1. Точка, яка лежить на осі ординат (0; 1)

2. Початок координат. (0; 0)

3. Точка, яка лежить на осі абсцис. (1; 0)

4. Початок координат. (0;0)

5. Координати середини точок (1; 1) та (3; 3) : (2; 2)

6. Координати середини точок (1; -1) та (3; -3) : (2; 2)

7. Координати середини точок (-1; -1) та (-3; -3): (-2; -2)

МОЛОДЦІ.

VІІІ. Завдання додому.

Повторити параграф 3, п. 8 підручника, стор.79-82.

Розв’язати № 324, 325, 326 .

Згадати теоретичний матеріал з теми «Коло».

За бажанням удома пропонується виконати творче завдання: підготувати презентацію .

ІX. Перевірка очікуваних результатів.

1. Якщо ви були впевненими протягом уроку, то підніміть праву руку.

2. Якщо ви працювали творчо, то підніміть ліву руку.

3. Якщо вам було цікаво долати перешкоди, сплесніть у долоні.

4. Якщо ви щиро раді за свої успіхи та успіхи товаришів, покладіть руку на серце.

5. Якщо хочете йти разом до вершини знань, візьміть один одного за руки і підніміть їх угору.

6. Якщо вам було приємно співпрацювати посміхніться один одному і скажіть: «Дякую за співпрацю!».

А я скажу вам: «Дякую за плідну співпрацю!».

Ось і закінчилась наша подорож до країни «Декартова система координат».

Зверніть, будь ласка, увагу на те, що у Вас на столах є конверти: у них знаходяться зображення графіка відомої Вам функції, зображеної на координатній площині. Скориставшись ними спробуймо відобразити свої враження від уроку.

Урок закінчено.

ВИСНОВКИ

«Від творчості вчителя -

до творчості учня»

Інновації в навчальному процесі – це вирішення проблеми розвитку та реалізації творчих здібностей кожного школяра. Саме такі нововведення зумовлені новими суспільними вимогами до соціалізації випускника тому, що інтенсивні зміни, які відбуваються в даний час в нашому суспільстві, вимагають ініціативної, успішної, творчої, креативно мислячої, компетентної, активної особистості, здатної до самоосвіти, саморозвитку, самореалізації, професійної кар’єри та орієнтують педагогів на новий рівень викладання і виховання учнів.

Сучасний урок – це передусім урок, на якому вчитель уміло використовує всі можливості для комплексного розвитку особистості дитини, активного формування їх інтелекту, глибокого засвоєння знань. Тільки у співпраці з учнями, у партнерстві учитель — учень пріоритетом є знання учнів, розуміння предмету. А завдання учителя – виплекати здібного учня на основі його природних здібностей, інтересів та схильності до математики.

Крім того, будь-який урок має відповідати організаційним, дидактичним, психологічним вимогам, які тісно пов’язані між собою.

Навчання учнів в сучасній школі неможливе без використання комп’ютерів. Інноваційні комп’ютерні технології сприяють розвитку особистості та організації продуктивної диференційованої діяльності учнів. На таких уроках вони сприймають комп’ютер як засіб для вивчення математики, а вчитель на уроці легко може систематизувати знання, показати динаміку розкриття даної теми, миттєво оцінити знання дітей, вказавши на помилки і при цьому дати можливість для їх виправлення.

Не менш важливим в роботі з обдарованими учнями є упровадження пошуково-дослідницької та проектної діяльності з метою формування компетентної особистості. Пріоритетними методами проектної діяльності залишаються методи стимулювання і мотивації навчання, дослідницької діяльності. Метод проектів зорієнтований на творчу самореалізацію особистості, яка розвивається в процесі навчання.

Використання на уроках математики інноваційних технологій сприяє професійному зростанню вчителя, змінює атмосферу на уроці, активізує роботу учнів, і як наслідок, покращується якість набутих знань. Звичайно, інновації потребують багато часу для підготовки вчителя, але отриманий результат того вартий.

Тому актуальним питанням сьогодення є використання інноваційних технологій на уроках математики. Адже саме їх вміле застосування допоможе вчителю виростити конкурентоспроможну людину. На кожному уроці важливим є опанування математичним матеріалом, що не можливо без поєднання предметного матеріалу з продуктивними інноваційними технологіями.

В процесі роботи над проблемою та проаналізувавши новітні педагогічні технології, які найбільш сприяють покращенню якості математичної освіти, я прийшла до висновку, що необхідно вивчати і застосовувати в практиці те, що відповідає потребам сьогодення та сприяє реалізації творчого потенціалу особистості в життєвій перспективі.

Справжній учитель не той, хто розкриває учневі таємниці

буття, вказуючи йому прямий шлях до храму науки, а той, хто своєю мудрістю запалює сонце над головою дитини, викрешуючи іскру допитливості, спонукаючи самостійно відшукати ключ до знань.