Тим, хто вчить математику,

  Тим, хто вчить математики,

Тим, хто любить математику,

  Тим, хто знає математику,

  Тим, хто ще не знає,

Що він любить математику

 

 

 

Числа — це невід’ємне знаряддя сучасної цивілізації, що використовується для впорядкування сфери її діяльності.

Ф. Дейвіс

 

 

 

Підготувала

 вчитель математики та інформатики

 Поберезького навчально-виховного комплексу

Пушко Орися Володимирівна

ДІЛЬНИКИ І КРАТНІ НАТУРАЛЬНОГО ЧИСЛА.

ПРОСТІ ЧИСЛА

 

Дільником числа називають таке число, на яке ділиться дане число.

 

Кратним числа називають таке число, яке ділиться на дане число.

Зверніть увагу! Кожне натуральне число, починаючи з числа 2, має принаймні два дільникки – число 1 і саме це число. Інші дільники шукають за спеціальними правилами.

Просте число – має лише два дільники (1 і самого себе)

Складене число – має більше, ніж два дільники.

1. – ні просте, ні складене

Властивості:

1. Найменше просте число 2.
2. Найбільшого немає.
3. Числа-близнята (пара простих чисел, різниця між якими становить 2): 3 і 5; 11 і 13; …

Решето Ератосфена

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30

ЗАДАЧІ

1. Жителі острова поділили між собою 48 зібраних кокосових горіхів порівну. Скільки жителів може бути на острові?
2. Яку найбільшу кількість мішків із цукром масою по 70 кг  можна навантажити на автомобіль вантажністю 3 т?
3. Розділіть 5 яблук, що є в корзині,  між 5 друзями так, щоб кожен отримав по яблуку і одне залишилося в корзині.
4. Шкільний автобус Поберезького  НВК розрахований на 24 місця.

1) Скільки школярів могло їхати до школи у вівторок якщо це число ділиться на 2 і 5?

 2)В четвер на районні змагання по баскетболу їхала шкільна команда. Яка була кількість учнів у автобусі, якщо це число більше за 6, менше за 16 і кратне 2 і 3?

5. Задача-жарт. Багатоголовий змій знає 105 слів, до того ж, кожна голова знає однакову кількість слів і різні голови не знають одного і того ж слова. Скільки голів у змія, якщо їх більше, ніж 10, але менше, ніж 20? Яку найменшу кількість голів потрібно задіяти змієві, щоб вимовити 40 різних відомих йому слів?

ОЗНАКИ ПОДІЛЬНОСТІ НА 2, 10, 5

Парні числа – числа, що кратні 2.

Парні цифри – це 0, 2, 4, 6, 8.

2п         – формула парного числа

де п – деяке натуральне число.

Непарні числа – числа, що не діляться на 2.

2п – 1      – формула непарного числа

де п – деяке натуральне число.

Ознака подільності на 2: на 2 діляться ті і тільки ті числа, запис яких закінчується парною цифрою.

Ознака подільності на 10: на 10 діляться ті і тільки ті числа, запис яких закінчується цифрою 0.

Ознака подільності на 5: на 5 діляться ті і тільки ті числа, запис яких закінчується або цифрою 5, або цифрою 0.

Зверніть увагу! Серед чисел, які діляться на 5, парні числа діляться і на 10, а непарні – ні.

 

Ознака подільності на 4: число ділиться на 4 тоді і тільки тоді, коли на 4 ділиться число, утворене двома останніми цифрами даного числа.

Ознака подільності на 8: число ділиться на 8 тоді і тільки тоді, коли на 8 ділиться число, утворене трьома останніми цифрами даного числа.

Ознака подільності на 25: число ділиться на 25 тоді і тільки тоді, коли на 25 ділиться число, утворене двома останніми цифрами даного числа.

Ознака подільності на 125: число ділиться на 125 тоді і тільки тоді, коли на 125 ділиться число, утворене трьома останніми цифрами даного числа.

 

Захоплення Софії Ковалевської 

наукою почалося ще з раннього дитинства, коли через брак шпалер батьки обклеїли кімнату дівчинки листками з лекціями вченого-математика. Так Софія познайомилася з диференціальним й інтегральним численням.

 

 

ЗАДАЧІ

1. Сергій купив п’ять однакових зошитів. Продавець сказав, що Сергій повинен заплатити 3 грн. 48 к. Чи не помилився продавець?

 

2. Чи можна розкласти 50 яблук на 5 купок, у кожній з яких буде непарна кількість яблук? Відповідь поясніть.

 

3. Чи існує прямокутник, довжини сторін якого виражені натуральними числами в сантиметрах, причому одна з них на 1 см довша за іншу, і площа якого дорівнює 12 345 ?

 

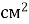4. У школі працюють два нічних охоронці: Іван Іванович і Петро Петрович. Вони працюють по черзі з вечора до ранку наступного дня. Іван Іванович заступив на чергування 1 вересня, Петро Петрович — 2 вересня. Хто з них заступить на чергуван­ня 18 вересня? 29 вересня? 1 жовтня? 30 жовтня? 31 жовтня? По яких числах — парних чи непарних — чергуватиме Іван Іванович у листопаді? Хто з них чергуватиме в ніч на Новий рік?

 

ОЗНАКИ ПОДІЛЬНОСТІ НА 9, 3

Ознака подільності на 9: на 9 діляться ті і тільки ті числа, сума цифр яких ділиться на 9.

 

Наприклад:

            387 ділиться на 9, бо 3 + 8 + 7 = 18 9

 

Ознака подільності на 3: на 3 діляться ті і тільки ті числа, сума цифр яких ділиться на 3.

Наприклад:

            831 ділиться на 3, бо 8 + 3 + 1 = 12 3

 

 

а 12, якщо число а ділиться на 3 і 4;

а 15, якщо число а ділиться на 3 і 5;

а 18, якщо число а ділиться на 2 і 9.

А чи знаєте ви , що англійська королева , прочитавши книгу Льюїса Керрола « Аліса в країні чудес» , так зацікавилась нею , що наказала принести їй всі книжки цього письменника , але була розчарована , тому що в інших книгах були математичні формули.

ЗАДАЧІ

1.     Ольга задумала трицифрове число. Про нього вона лише повідомила: «Першою цифрою числа є 1, воно ділиться на 9 і на 5, але не ділиться на 2». Яке число задумала Ольга?
2.     Оксана забула першу цифру коду замка *15421, але пам'ятає, шо це число ділиться на 3. Скільки варіантів коду потрібно перевірити Оксані, щоб потрапити додому?
3.     Сергій знайшов добуток усіх чисел від 1 до 11 включно і записав результат на дошці. На перерві хтось випадково витер три цифри, і на дошці залишився запис 399*68**. Не виконуючи множення повторно, відновіть витерті цифри.
4.     Роман і Дмитро записують дев’ятнадцятицифрове число, використовуючи тільки цифри 1, 2 і 4. Першу цифру пише Роман, другу — Дмитро, третю — знову Роман і т. д. по черзі. Роман хоче отримати в результаті число, кратне 3. Чи може Дмитро завадити йому це зробити?
5.     Галина Петрівна придбала 3 пакети кефіру, пачку масла за 15 грн 60 к., кілька хлібин по            4 грн 35 к.,   6 коробок сірників. Чи може вся її покупка коштувати 72 грн 80 к.?

РОЗКЛАДАННЯ ЧИСЕЛ НА ПРОСТІ МНОЖНИКИ. НАЙБІЛЬШИЙ СПІЛЬНИЙ ДІЛЬНИК

Кожне складене число можна розкласти на 2 чи більше простих множників.

                15 = 5 • 3;        24 = 2 • 2 • 2 • 3 = 2³ • 3.

Розклад числа на множники, у якому всі множники – прості числа, називається розкладом числа на прості множники.

Щоб розкласти складене число на прості множники, виконуй дії, подібні до прикладу:     

        2100   2

        1050   5

          210   5

           42    2

           21    3

             7    7

             1                                2100 = 2² • 5²  3 • 7

Найбільший спільний дільник двох чисел – найбільше натуральне число, на яке ділиться кожне з даних чисел.

      НСД (18; 24) = 6

Щоб знайти  найбільший  спільний  дільник потрібно:

1. Розкласти числа на прості множники.
2. Знайти спільні множники.
3. Знайти добуток із спільних множників з найменшим показником.

НСД (210; 75) = 3  • 5 = 15

210. 2         75   5                210 = 2 • 3  • 5  • 7;

105. 5         15   5                          75 = 3  • 5²

21. 3           3   3

7. 7           1

Числа взаємно прості, якщо НСД = 1

НСД (6; 25) = 1

6 = 2 • 3;        25 = 5 • 5;              6 і 25 – взаємно прості

А чи знали ви , що квітку гортензію назвали на честь Гортензії Лепот, відомої обчислювальниці , що складала математичні таблиці ? Вона привезла цю квітку з Індії

 

ЗАДАЧІ

1. Між учнями 6 класу поділили порівну 155 зошитів і 62 ручки. Скільки в цьому класі учнів?
2. На автомобілі навантажили 96 контейнерів з картоплею та 64 контейнери з капустою. Скільки було автомобілів, якщо відомо, що їх не менше ніж 20 і на всіх автомобілях була однакова кількість контейнерів з картоплею та однакова кількість контейнерів з капустою?
3. Між шкільними бібліотеками поділили                      92 тлумачних і 138 орфографічних словників української мови. Скільки було шкіл, якщо відомо, що їх не менше ніж 25 і всі школи отримали однакові комплекти зі словників двох видів?
4. Для новорічних подарунків прид   96 шоколадок,     72 апельсини та 84 банани. Яку найбільшу кількість однакових подарунків можна з них 5. Найбільший спільний дільник 41 скласти, якщо треба використати всі продукти? Скільки окремо шоколадок, апельсинів і бананів буде в кожному подарунку?
5. Зі 156 жовтих, 234 білих і 390 червоних троянд складали букети. Яку найбільшу кількість однакових букетів можна скласти, якщо треба використати всі квіти?
6. Діти отримали на новорічній ялинці однакові подарунки. У всіх подарунках разом було 123 апельсини і 82 яблука. Скільки дітей було присутньо на святі? Скільки апельсинів і скільки яблук було в кожному з подарунків?
7. У кімнаті завдовжки 625 см і завширшки 475 см вирішили викласти долівку однаковими декоративними плитками квадратної форми, не розрізуючи їх. Який найбільший можливий розмір такої плитки? Скільки плиток найбільшого розміру потрібно, щоб викласти ними долівку?

 

 

 

 

КРАТНІ НАТУРАЛЬНОГО ЧИСЛА.

НАЙМЕНШЕ СПІЛЬНЕ КРАТНЕ

 

Кратне даному числу – це будь-яке натуральне число, яке ділиться на дане натуральне число.

Найменше спільне кратне двох чисел – найменше натуральне число, яке ділиться на кожне з даних чисел.

НСК (9; 12) = 36

Щоб знайти  найменше  спільне  кратне потрібно:

1. Розкласти числа на прості множники.
2. Знайти добуток із всіх множників з найбільшим показником.

НСК (9; 75) = 3²  • 5² = 225

  9      3         75     5

  3      3         15     5

1                   3     3

                                      1

                9 = 3²;            75 = 3  • 5²

НСК двох взаємно простих чисел є добуток цих чисел.      

НСК (8; 9) = 72

ЗАДАЧІ

1. З одного місця в одному напрямі по велотреку одночасно стартували два велосипедисти. Один із них робить коло за 1 хв, а другий — за 45 с. Через яку найменшу кількість хвилин після початку руху вони знову одночасно зустрінуться в місці старту? Скільки кіл по велотреку при цьому проїде кожний із них?
2. Дмитро й Петро вирушили в похід з одного пункту в одному напрямі. Петро робив зупинку для відпочинку через кожні 2400 м, а Дмитро — через кожні 2800 м. На якій найменшій відстані від пункту відправлення їхні зупинки збігатимуться?
3. У ящику менше ніж 80 мандаринів. Відомо, що їх можна поділити порівну між двома, трьома або п’ятьма дітьми, але не можна поділити порівну між чотирма дітьми. Скільки мандаринів є в ящику?
4. Сашко ходить до басейну один раз на 3 дні, Юрко — раз на 4 дні, Петрик — раз на 5 днів. Вони зустрілися в басейні у вівторок. Через скільки днів і в який день тижня вони зустрінуться наступного разу?
5. Готуючи новорічні подарунки, члени батьківського комітету 6 класу побачили, що цукерки, які в них є, можна розкласти порівну по 15 штук або по 20 штук в один подарунок. Скільки було цукерок, якщо відомо, що їх було більше за 600 і менше від 700?
6. У портовому місті починаються три туристичних рейси, перший з яких триває 15 діб, другий – 20, третій – 12 діб. Повернувшись до порту, теплоходи того ж дня вирушають у новий рейс. Сьогодні з порту вийшли теплоходи за всіма трьома маршрутами. Через скільки діб вони знову разом вийдуть у плавання?

 

 

ОСНОВНА ВЛАСТИВІСТЬ ДРОБУ.

СКОРОЧЕННЯ ДРОБУ

 

Основна властивість дробу:

Якщо чисельник і знаменник дробу помножити або поділити на одне й те саме число, відмінне від нуля, то одержимо дріб рівний даному.

при с

 

і - різні записи одного й того ж дробу

 

Ділення чисельника і знаменника дробу на їх спільний дільник, відмінний від одиниці, називають скороченням дробу

Правило скорочення дробу:

Щоб скоротити даний дріб, треба:

1. Для чисельника і знаменника дробу знайти

 спільний дільник, що не дорівнює 1.

 

2. Поділити знаменник дробу на спільний дільник

 і результат записати в знаменнику нового дробу.

 

3. Поділити чисельник дробу на спільний дільник

 і результат записати в знаменнику нового дробу.

 

 Нескоротний дріб – чисельник і знаменник дробу

 взаємно прості числа

    -    нескоротний дріб 

 

 

Американський вчений Джордж Данциг, навчаючись в університеті, немало здивував тамтешніх професорів. Одного разу, запізнившись на лекцію, він застав тільки порожню аудиторію зі списаної дошкою. Студент подумав, що на ній залишено домашнє завдання, акуратно переписав його і пізніше приніс готовий розв’язок. Виявилося, це були два рівняння статистики, які доти ще ніхто не розв’язував.

ЗАДАЧІ

1. Маса кавуна дорівнює 3 кг 200 г. Знайдіть у грамах    маси кавуна;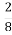 його маси. Порівняйте ці маси.
2. Мама купила дітям молочний шоколад, у якому      18 часточок. Тетянка сказала, що з’їла плитки шоколаду, а Іванко сказав, що з’їв 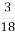 плитки. Мама сказала, що кожний з дітей з ‘їв однакову частину плитки шоколаду. Чи так це?
3. Маринка сказала, що розв’язала контрольну роботу швидше, ніж Катруся. З’ясуйте, чи права була дівчинка, якщо Маринка витратила на розв’язання контрольної роботи 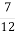  год, а Катруся – 35 хв.
4. Запишіть у хвилинах час, протягом якого триває:        1) 1 урок; 2) 2 уроки; 3) 4 уроки; 4) 6 уроків. Отримане число перетворіть у години та подайте у вигляді нескоротного дробу.
5. Тато купив 2 кавуни загальною масою 12 кг. Обидва кавуни поділили порівну між усіма членами родини: татом, мамою, двома бабусями, двома дідусями, Оленкою та її братиком Назаром. Яка маса (у кілограмах) тієї частини кавунів, що дістанеться кожному члену родини? Отримане число скоротіть.

ЗВЕДЕННЯ ДРОБІВ ДО СПІЛЬНОГО ЗНАМЕННИКА. ПОРІВНЯННЯ ДРОБІВ

Звести дріб до нового знаменника означає помножити його чисельник і знаменник на одне й те саме число.

Наприклад: записати дріб    із знаменником 12        

- потрібно 12 : 4;

  або із знаменником 24

- потрібно 24 : 4.

 

Числа 3 і 6, на які ми множили чисельники і знаменники називаються додатковими множниками.

 

Зверніть увагу!

• додатковий множник є натуральним числом;
• щоб знайти додатковий множник, поділіть новий знаменник на знаменник даного дробу.

 

Найменшим спільним знаменником двох дробів називають найменше спільне кратне знаменників цих дробів.

Щоб звести дроби до найменшого спільного знаменника, потрібно:

1. знайти найменше спільне кратне  знаменників;
2. знайти додаткові множники для кожного дробу, поділивши НСК знаменників на знаменник кожного дробу;
3. чисельник і знаменник кожного дробу помножити на відповідний додатковий множник.

і зведемо до найменшого спільного знаменника

;           .

7 і 5 – додаткові множники.

 

Щоб порівняти дроби з різними чисельниками і знаменниками, досить звести їх до спільного знаменника і порівняти одержані дроби.

ЗАДАЧІ

1.  Батько Наталі виготовив 42 однакові деталі за      5 год, а батько Ірини 60 таких же деталей — за      7 год. Хто витрачав на виготовлення однієї деталі більше часу?
2. У 21 кг рису міститься 16 кг крохмалю, а у 12 кг ячменю — 7 кг крохмалю. Де крохмалю більше — в 1 кг рису чи в 1 кг ячменю?
3.  На тренуванні перший стаєр пробіг 9 км за 36 хв, другий — 11 км за 48 хв, а третій — 17 км за       72 хв. Хто зі стаєрів пробігав за хвилину найбільшу відстань, а хто — найменшу?
4.  За 10 кроків Оля проходить 6 м, а Таня за 17 кроків — 12 м. Чий крок коротший — Олі чи Тані?
5. Трьохметрову колоду розпиляли на 7 рівних частин, а п'ятиметрову — на 9 рівних частин. Частини якої колоди довші?
6. Відстань між двома містами легковий автомобіль долає за 4 год, а вантажний — за 7 год. Який автомобіль проїде більшу відстань: легковий за      3 год чи вантажний за 5 год?
7.  Теплохід проходить відстань між двома пристанями за 9 год, а катер — за 6 год. Порівняйте відстань, яку пройде теплохід за 7 год, з відстанню, яку пройде катер за 5 год.

 

ДОДАВАННЯ І ВІДНІМАННЯ ДРОБІВ З РІЗНИМИ ЗНАМЕННИКАМИ

Щоб додати або відняти дроби з різними знаменниками, потрібно:

1. звести дроби до найменше спільного знаменника;
2.               додати або відняти дроби з однаковими знаменниками.

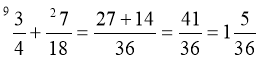
Закони додавання:

• переставний:

 

 

 

 

• сполучний:

 

 

 

 

 

 

ЗАДАЧІ

1. Власна швидкість теплохода становить                  20 км/год, а швидкість течії річки дорівнює         2 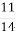км/год. Знайдіть швидкість теплохода за течією річки та його швидкість проти течії.
2. У трьох ящиках було 36 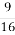кг груш. У першому та другому ящиках було 28 кг груш, а в першому та третьому — 24 кг. Скільки кілограмів груш було в кожному ящику?
3. На комп’ютері опрацьовували три задачі впродовж 30 хв. На першу та другу задачі було витрачено        24 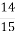хв, а на другу та третю —       18 хв. Скільки часу було витрачено на опрацювання кожної задачі?
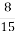4. Для приготування 6 кг крему кухар узяв 3 кг молока, 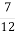кг какао та цукор. Скільки кілограмів цукру взяв кухар для приготування крему?
5. Для виготовлення 12 кг морозива взяли 7 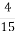кг води, 2 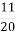кг молочного жиру,  1 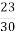кг цукру та фруктовий сироп. Скільки кілограмів сиропу взяли для виготовлення морозива?
6. Перший робітник може пофарбувати паркан за         15 год, другий — за 12 год, а третій — за 10 год. Яку частину паркану вони пофарбують разом за     1 год? за 2 год? за 4 год?
7. Михайлик може з’їсти кавун за 12 хв, а Миколка — за 16 хв. Яка частина кавуна залишиться через   1 хв, якщо хлопчики почнуть їсти його одночасно?
8. Басейн можна наповнити водою за 6 год через одну трубу й спорожнити за 10 год через другу. Басейн був порожнім, коли Остап Забудько відкрив крани одночасно на обох трубах. Яка частина басейну залишиться незаповненою водою через 1 год після того, як Остап відкрив крани?
9. Олена та Марія можуть разом набрати на комп’ютері деякий текст за 6 год. Яку частину тексту набере Олена за 1 год, якщо Марія може набрати весь текст за 9 год?

 

Чи знаєте ви, чому рівна сума всіх цілих чисел від 1 до 100? Розповідають, що коли 9-річному Гаусу (видатний німецький математик) учитель запропонував знайти суму всіх цілих чисел від 1 до 100, то маленький Гаус сам зрозумів, яким способом можна дуже швидко виконати цю операцію. Треба складати перше число з останнім, друге з передостаннім і т. д. Сума кожної такої пари чисел дорівнює 101 і повторюється вона 50 разів. Отже, сума всіх цілих чисел від 1 до 100 буде дорівнює                  101 * 50 = 5050.

МНОЖЕННЯ ЗВИЧАЙНИХ ДРОБІВ

 

Добутком двох звичайних дробів є дріб, чисельник якого дорівнює добутку чисельників цих дробів, а знаменник - добутку їх знаменників.

 

  - і, якщо можна скоротіть.

 

До спільного знаменника зводити не треба!

 

 

Щоб помножити дріб на ціле число, достатньо його чисельник помножити на це число, а знаменник залишити без зміни.

 

 

Щоб помножити мішані дроби, потрібно перетворити ці дроби в неправильні і застосувати правило множення дробів.

 

Властивості множення:

• переставна        
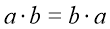
• сполучна            
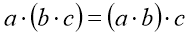
• розподільна       
• 

 

 

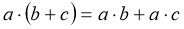
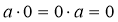
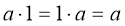
ЗАДАЧІ

1. Довжина кімнати дорівнює 6 м, її ширина становить 75% довжини, а висота — ширини. Знайдіть масу повітря в цій кімнаті, якщо 1 повітря має масу 1,29 кг.
2. До магазину завезли 1,2 т картоплі. За перший день продали 0,2 усієї картоплі, а за другий —   решти. Скільки кілограмів картоплі продали за другий день?
3. Задача Піфагора. Якось Полікрат (тиран з острова Самос) під час відвідин Піфагора запитав, скільки в нього учнів. «З радістю скажу тобі, о Полікрате, — відповів Піфагор. — Половина моїх учнів вивчає прекрасну математику, четвертина досліджує таємниці вічної природи, сьома частина вправляється силою... . Додай до них ще трьох юнаків, з яких Теон має найкращі здібності. Стільки учнів веду я до розуміння вічної істини». Скільки учнів було в Піфагора?
4. Велосипедист за першу годину подолав 40% дистанції, а за другу — 70%  решти дистанції. Скільки відсотків дистанції проїхав велосипедист за ці дві години?
5. Автотуристи проїхали 520 км за 4 дні. За перший день вони проїхали ,  за другий —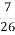  усього шляху, а за третій — на 40 км менше, ніж за четвертий. Скільки кілометрів проїхали автотуристи за четвертий день?
6. Перший трактор може зорати поле за 3 дні, а другий — за 4 дні. Чи зможуть трактори, працюючи разом 2 дні, зорати все поле?
7.  Один кран наповнює ванну за 15 хв, а інший — за 12 хв. Чи наповниться ванна, якщо обидва крани відкрити на 6 хв?

 

ДІЛЕННЯ ДРОБІВ.

ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ

 

Правило 1. Щоб поділити один дріб на інший, досить ділене помножити на число, обернене до дільника.

Наприклад:

Зверніть увагу! Якщо 1 поділити на дріб, то тримаємо дріб, обернений до даного.

Наприклад: 1 :

Правило 2. Щоб знайти число за його дробом, потрібно дане число, що виражає частину шуканого, поділити на цей дріб.

Правило 3. Щоб поділити мішані дроби, потрібно перетворити ці дроби в неправильний дріб і виконати ділення двох дробів.

Наприклад:

ЗАДАЧІ

1. Постамент із граніту має форму прямокутного паралелепіпеда. Його ширина дорівнює м, що становить   довжини і 37,5% висоти. Знайдіть масу постаменту, якщо 1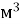  граніту має масу      2,7 т.
2.  Дорога до міста складається з підйомів, спусків та горизонтальних ділянок. Підйоми становлять 30% усього шляху, спуски — 70% підйомів, а решта 24,5 км — горизонтальні ділянки. Знайдіть довжину дороги. 
3. До магазину завезли яблука, груші й сливи. Маса яблук становить 60%  завезених фруктів, маса груш — 25%, а решта 45 кг — сливи. Скільки кілограмів яблук і груш окремо завезли до магазину?
4.  Дві снігоприбиральні машини, працюючи разом, можуть прибрати сніг з вулиці за 6 год. Після 3-х годин спільної роботи першу машину направили в інший район міста, а друга закінчила роботу за       5 год. За скільки годин кожна машина, працюючи окремо, може виконати всю роботу?
5. Для вирівнювання дороги використали дві грейдерні машини різної потужності. Одна з них може виконати деяку роботу за 20 год, а інша — за 30 год. За який час дві грейдерні машини можуть виконати роботу, працюючи разом?
6. Мама залишила для трьох синів тарілку слив, а сама пішла на роботу. Першим зі школи прийшов молодший син, він побачив на тарілці сливи, з'їв третю частину і пішов гуляти. Другим прийшов середній син. Подумавши, що його брати ще не ласували сливами, він з'їв третю частину тих, що були на тарілці, й теж пішов гуляти. Останнім прийшов старший син і з'їв 4 сливи — третю частину тих, що були на тарілці. Скільки слив було на тарілці спочатку?

 

Наполеон Бонапарт писав математичні роботи і один геометричний факт називається «Задача Наполеона».

 

 

ВІДНОШЕННЯ ТА ЙОГО ВЛАСТИВОСТІ.

ПРОПОРЦІЯ ТА ЇЇ ВЛАСТИВОСТІ

Відношенням двох чисел називають частку цих чисел.

Записують: a:bабо

де аі b – члени відношення

 

Відношення вказує, у скільки разів одне число більше від іншого, або яку частину становить одне число від іншого.

4 : 6 = 2 : 3

 

Основна властивість  відношень:

відношення не зміниться, якщо кожне з чисел відношення помножити або поділити на одне й те ж, відмінне від нуля, число.

1,5 : 2,5 = 15 : 25 = 3 : 5.

 

Пропорція – рівність двох відношень.

a : b = c : dабо

a, d – крайні члени пропорції

b, c – середні члени пропорції

 

Основна властивість пропорції:

У правильній пропорції добуток крайніх членів дорівнює добутку середніх членів і навпаки.

ad  = bc

 

Щоб знайти крайній член пропорції, потрібно добуток її середніх членів поділити на інший крайній член.

 

Щоб знайти середній член пропорції, потрібно добуток її крайніх членів поділити на інший середній член.

Правило: якщо в правильній пропорції поміняти місцями середні члени або крайні члени, то отримаємо нові правильні пропорції.

a : c = b: d;d: b = c : a;

d: c = b: a

 

Г.Ф. Вороний належить до когорти найвідоміших українських математиків минулого. Визнаний фахівцями як один із найяскравіших талантів у галузі теорії чисел на межі ХІХ-ХХ століть, Г.Ф. Вороний за своє життя встиг надрукувати всього дванадцять статей. Але яких! Вони дали поштовх для розвитку кількох нових напрямів в математиці, які нині активно розвиваються у багатьох країнах.

ЗАДАЧІ

1. Скільки кілограмів води варто додати до 7,5 кг 12%-го розчину солі, щоб одержати 10% розчин?
2. У зоопарку були мавпи різних порід: горили, шимпанзе й орангутанги. Найбільше було вертких шимпанзе, аж 18, поважно походжали горили, кількість яких становила  від кількості шимпанзе, спокійно розглядали відвідувачів орангутанги, яких було вдвічі менше, ніж горил. Яку частину всіх мавп становили горили?
3. 0,3 кг сиру коштує 21 грн. 60 к., а 250 г бринзи – 16 грн. У скільки разів кілограм сиру дорожчий від кілограма бринзи?
4. 0,4 кг цукерок коштує 38 грн. 40 к., а 200 г печива – 9 грн. 60 к. У скільки разів кілограм цукерок дорожчий від кілограма печива?
5. Андрій пройшов 2 км за 0,5 год, а черепаха проповзла 20 м за 15 хв. У скільки разів швидкість учня більша від швидкості черепахи?
6. Цукровий буряк, який є найсолодшою коренеплідною рослиною в Україні, накопичує до 25% цукру, тоді як цукрова тростина — лише 18%. Скільки тонн цукрової тростини треба переробити, щоб отримати стільки ж цукру, як із 3600 т цукрових буряків?

 

7. Щоб зварити 4 порції манної каші, узяли 220 г манних крупів, 960 г молока та 50 г цукру. Скільки грамів кожного із цих продуктів потрібно взяти, щоб зварити 18 порцій каші?
8. Щоб отримати 120 кг мельхіору, треба сплавити 18 кг нікелю, 24 кг цинку, а решту — міді. Скільки кілограмів кожного металу треба взяти, щоб отримати 164 кг мельхіору?

 

 

ПРЯМА ТА ОБЕРНЕНА ПРОПОРЦІЙНІ ЗАЛЕЖНОСТІ. ПОДІЛ ЧИСЛА В ДАНОМУ ВІДНОШЕННІ. МАСШТАБ

Пряма пропорційність– цепропорційність, при якій при збільшенні (зменшенні) однієї величини у кілька разів, інша величиназбільшується (зменшується)у стільки ж разів.

Зверніть увагу!

Якщо дві величини прямо пропорційні, то пропорцію утворюють відношення відповідних значень цих величин.

Обернена пропорційність–цепропорційність, при якій при збільшенні (зменшенні) однієї величини у кілька разів,інша величиназменшується (збільшується) у стільки ж разів.

Зверніть увагу!

Якщо дві величини обернено пропорційні, то пропорцію утворюють взаємно обернені відношення відповідних значень цих величин.

Коефіцієнт пропорційності – число, яке дорівнює значенню відношення пропорції.

Позначають: k – коефіцієнт пропорційності

Масштаб карти – це відношення довжини відрізка карти до довжини відповідного відрізка на місцевості.

М  1 : 1000

Це означає: 1 см на карті відповідає 1000 см на місцевості

Масштаб показує, в  скільки разів відстань на малюнку, кресленні, плані чи карті менша за відстань на місцевості.

 

 

ЗАДАЧІ

1. За 36 робочих днів бригада лісорубів із 30 осіб заготовила 1944 м³ дров. Продуктивність праці всіх лісорубів однакова. Скільки дров заготовить бригада із 24 чоловік за 50 днів за такої ж продуктивності праці?
2. Для того щоб побудувати стіну завдовжки 18 м, завтовшки 0,5 м і заввишки 3 м, потрібно 10 800 цеглин.Якої висоти стіну завдовжки 15 м, завтовшки 0,25 м можна побудувати, маючи 5 400 цеглин?
3. Сплав складається з міді, олова і сурми, взятих у відношенні 1:2:2. Знайдіть масу сплаву, якщо він містить 2,8 кг олова.
4. У будинку є двокімнатні, трикімнатні та чотирикімнатні квартири, всього 180 квартир. Число двокімнатних квартир відноситься до числа трикімнатних як 5 : 6, а число трикімнатних до числа чотирикімнатних — як 3 : 2. Скільки двокімнатних, трикімнатних і чотирикімнатних квартир є у будинку?
5. За m кг цукерок заплатили р грн. Користуючись таблицею, визначте ціну 1 кг цукерок. Заповніть таблицю. Задайте формулою залежність р від m .

m, кг	3	8		1,2
р, грн	225		300		60

6. Поїзд рухається зі швидкістю 60 км/год. Заповніть таблицю, у першому рядку якої вказано час руху t, а в другому — пройдений шлях s.

t, год	2	0,5		3,2
s, км	90		240		156

7. Бригада з 15 робітників може відремонтувати школу за 46 днів. Скільки потрібно робітників, щоб відремонтувати цю школу за 30 днів, якщо продуктивність праці всіх робітників однакова?
8. Геракл заготував для 240 коней царя Авгія кормів на 19 днів. На скільки днів вистачить цих кормів, якщо коней у царя Авгія стане 304, а всі коні споживають однакову кількість корму?
9. Троє мулярів працювали з однаковою продуктивністю й отримали за свою роботу      4000 грн. Скільки гривень має отримати кожний муляр, якщо перший із них працював 16 год, другий — 24 год, а третій — 40 год?
10. Як треба поділити 540 т сіна між трьома фермами, якщо на першій фермі 28 корів, на другій —         42 корови, а на третій — 65 корів?
11. Фруктовий сад на плані 1:25 000 має форму прямокутника зі сторонами 8мм і 6мм. Яка площа саду на місцевості?
12. На місцевості відстань від школи до будинку 4км. На плані ця відстань дорівнює 4см. Який масштаб плану?

ЙМОВІРНІСТЬ ВИПАДКОВОЇ ПОДІЇ

 

Випадкова подія – це явище, про яке можна сказати, що воно відбудеться чи не відбудеться за певних умов.

Позначають: А, В, С.

Випробування – це експеримент, під час якого відбувається подія.

Зверніть увагу!Усі можливі результати випробування утворюють сукупність подій, проте випробування завершується настанням лише однієї із цих подій.

Достовірна подія – це подія, яка в результаті випробування неодмінно має статися.

Неможлива подія – подія, яка внаслідок випробування не може відбутися.

Несумісні події – якщо поява однієї з них виключає появу другої.

Рівноможливі події – якщо в результаті випробування поява кожної з них є однаково можливою порівняно з іншими.

Ймовірність події – це кількісна характеристика можливості настання цієї події в ході випробування.

Ймовірністю подіїА називається відношення кількості т сприятливих для А подій до кількості п усіх рівноможливих у даному випробуванні подій:

.

Зверніть увагу!

1. Ймовірність події може набувати значень лише від 0 до 1.
2. Ймовірність достовірної події = 1.
3. Ймовірність неможливої події = 0.
4. Сума ймовірностей усіх можливих подій випробування = 1.

А чи знаєте ви, що першим запропонував метод нумерації стільців у театрі за рядами і стільцями Рене Декарт? Аристократи-театрали не переставали докучати королю з проханнями нагородити вченого. Але той опирався, відповідаючи: «Так, те що придумав Декарт - чудово, так, воно достойне ордена! Але дати його філософу?! Ні, це : занадто!»

ЗАДАЧІ

1.  Набираючи номер телефону, Іра забула останню цифру, тому набрала її навмання. Знайдіть імовірність того, що номер набрано правильно.
2. У школі є два шостих класи — 6-А та 6-Б. У 6-А класі навчається 16 дівчат і 12 хлопців, а в 6-Б —     14 дівчат і 16 хлопців. Знайдіть імовірність того, що шестикласник, якого ви зустрінете, є:               а) дівчиною;   б) хлопцем із 6-Б класу.
3. Цукерки «Карамель» розклали у три пакети: у перший пакет поклали 15 цукерок, у другий — 25, а у третій —30, до того ж, у кожен пакет поклали по     3 шоколадні цукерки. З якого пакета ймовірність вийняти шоколадну цукерку є найбільшою, а з якого — найменшою? Знайдіть ці ймовірності.
4. У ящику було 45 куль, з яких 17 — білі. Загубили дві небілі кулі. Яка ймовірність того, що взята навмання куля буде білою?
5. Картки з номерами 1, 2, 3 поклали в ряд. Яка ймовірність того, що картки з непарними номерами опиняться поруч?
6. У коробці лежать 2 синіх кулі та кілька червоних. Скільки червоних куль у коробці, якщо ймовірність того, що вибрана навмання куля:

 1) виявиться синьою, дорівнює ;

2) виявиться червоною, дорівнює ?

7.  У коробці лежать 3 зелених і 6 синіх куль. Яку найменшу кількість куль треба вийняти навмання, щоб ймовірність того, що серед вийнятих куль хоча б одна буде зеленого кольору, дорівнювала 1?

8. Кожну з граней кубика пофарбовано в один із двох кольорів — синій або жовтий. Ймовірність того, що при киданні кубика випаде синя грань, дорівнює. Скільки синіх і скільки жовтих граней  у кубика?

 

ВІДСОТКОВІ РОЗРАХУНКИ

 

1. Знаходження відсотка від числа

 

 Правило:  Щоб знайти число х, яке становитьd числа а, складають пропорцію:

а – 100%      

х – d

2. Знаходження числа за його відсотком

 

 Правило:  Щоб знайти число х за його частиною b, яке становитьd, складають пропорцію:

х – 100%      

b – d

3. Знаходження відсоткового відношення двох чисел

 

Правило:  Щоб знайти відсоткове відношення двох чисел а і b, складають пропорцію:

а – 100%      

b – х

 

 

4. Знаходження зміни відсотка за зміною числа

 

Правило:  Щоб знайти зміну відсотка х за зміною числа а до числа b, складають пропорцію:

а –             100%         100 +

b – (100 + х)

 

5. Знаходження числа за його відсотковою зміною

 

Правило:  Щоб знайти число х, яке змінилося до числа b, за його відсотковою зміною п, складають пропорцію:

х –             100%         

b – (100 + п)

 

6. Знаходження відсоткового відношення двох чисел за зміною числа

 

Правило:  Щоб знайти відсоткове відношення двох чисел а і а + п за зміною а на п, складають пропорцію:

             а –  100%         

а + п – х

 

ЗАДАЧІ

1.  З 1,6 га землі, що становить 8% площі всього поля, зібрали 48 ц пшениці. Скільки центнерів пшениці зібрали з поля, якщо врожайність на усьому полі однакова?
2. Фермер засіяв соняшником 1,8 га поля, що на 20% більше, ніж торік. Яку площу фермер засівав соняшником торік?
3.    Гроші в сумі 14 000 грн., зібрані на благодійному концерті, були розподілені так: 45% грошей виділили для будинку дітей-сиріт, 42,5% — для будинку престарілих, а на решту коштів купили піаніно для музикальної школи. Скільки коштує піаніно?
4. Три робітники виготовили замовлену партію деталей. Перший і другий робітники виготовили відповідно 30% і 40% усіх деталей, а третій — на   8 деталей менше, ніж другий. Скільки всього деталей виготовили робітники?
5. Щоб урахувати інфляцію 4%, виробник холодильників підняв ціну на кожний холодильник з 1250 грн. до 1290 грн. Чи правильно він виконав розрахунки?
6. Вкладник вніс до банку 500 грн. під 14% річних, через рік річна ставка зросла до 17%. Яку суму грошей він матиме на рахунку через 2 роки?
7.  Банк дав підприємцеві кредит 20 000 грн. на          9 місяців зі ставкою 8% річних. Яку суму підприємець повинен повернути через 9 місяців?
8. Ціну на товар, що коштував 150 грн., спочатку збільшили на 20%, а потім нову ціну зменшили на 20%. Знайдіть ціну товару після двох переоцінок.
9. Ціну на товар, що коштував 100 грн., зменшили на 20%. На скільки відсотків потрібно підняти нову ціну, щоб отримати початкову?
10. Сплав міді з оловом масою 12 кг містить 45% міді. Скільки кілограмів чистого олова потрібно додати до сплаву, щоб одержати новий сплав, який містив би 40% міді?

 

А чи знаєте ви, що знаменитий Фалес був уболівальником і помер на трибуні Олімпійського стадіону, спостерігаючи за кулачним боєм Піфагора?

 

 

 

 

КОЛО. ДОВЖИНА КОЛА.

КРУГ. ПЛОЩА КРУГА

 

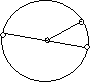                     А            точка  О         – центр кола;

В        О            С         відрізок ОА   – радіус кола, R;

                                     відрізок ВС   – діаметр кола, D.

Коло – це фігура, усі точки якої знаходяться на однаковій відстані від однієї точки, яка називається центром кола.

Діаметр кола – це відрізок, який сполучає дві точки на колі і проходить через центр.

D = 2R.

Діаметр кола удвічі більший від радіуса цього кола.

Дуга кола – це частина кола, яка знаходиться між двома точками, що лежать на колі.

– дуги кола.

  – півколо

;          3,1415…;   

Довжина кола дорівнює добутку числа й діаметра.

або  

 

 

 

 

Круг – внутрішня частина кола.

Центр, радіус, діаметр кола – центр, радіус, діаметр круга.

Сектор – частина круга, обмежена двома радіусами і дугою круга.

Увага!

• у рівних секторів – рівні кути;
•  сума кутів усіх секторів, на які поділено круг, дорівнює 360.

Діаметр розбиває круг на дві рівні частини, які називають півкругами.

Формула площі круга:      

 

ЗАДАЧІ

1. Хвилинна стрілка годинника описала півколо. За який час вона це зробила? За який час вона повернеться на чверть кола?
2. Діаметр колеса тепловоза дорівнює 80 см. За 2хв колесо робить 800 обертів. Яка швидкість тепловоза в кілометрах за годину? Результат округліть до десятих км/год.
3. Супутник рухається коловою орбітою на висоті   36 000 км над Землею і робить повний оберт навколо Землі за 24 год. З якою швидкістю рухається супутник, якщо радіус Землі дорівнює 6370 км?
4. Довжина кола арени цирку дорівнює 47,1 м. Знайдіть площу арени (результат округліть до одиниць м²).
5. Найбільший оптичний телескоп (рефлектор) в Україні знаходиться в Кримській астрономічній обсерваторії. Діаметр обода його дзеркала дорівнює 2,6 м. Найбільший у світі оптичний телескоп знаходиться в обсерваторії Каліфорнійського університету на Гавайях (США). Діаметр обода його дзеркала дорівнює     10 м. Знайдіть відношення довжин ободів дзеркал американського й українського телескопів. Відповідь округліть до десятих.
6. Піца, діаметр якої дорівнює 30 см, коштує стільки ж, скільки дві піци, діаметр яких 20 см. У якому випадку Дмитрик з’їсть більше піци: коли придбає одну велику чи дві менші, якщо всі піци мають однакову товщину?
7. Діаметр колеса автомобіля дорівнює 65 см. Автомобіль їде з такою швидкістю, що колеса роблять 6 обертів щосекунди. Знайдіть швидкість автомобіля в кілометрах за годину. Відповідь округліть до десятих.

 

Багато чого встиг зробити він за своє життя. Головна праця «Початки». У ній підвелено підсумки попереднього стану грецької математики, створено фундамент для її розвитку. «Початки» складаються з 13 книг. Перша містить найважливіші положення про фігури, їхні сторони , кути і площі, про перпендикулярні прямі, паралелограми та їх площі. В інших можна знайти теорію раціональних величин і цілих чисел, дано основи елементарної стереометрії. Одного разу цар Птолемей запитав у Евкліда, чи немає в геометрії коротшого шляху для її вивчення, ніж той, що пропонує він. На що вчений відповів: «Для царів немає окремого шляху в геометрії»

ДІАГРАМИ.

ЦИЛІНДР. КОНУС. КУЛЯ

 

Для наочного зображення частин цілого або співвідношення величин використовують діаграми.

Види діаграм: кругова і стовпчаста.

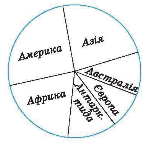
Для побудови кругової діаграми ціле зображують кругом, а окремі частини цілого – секторами.

 

Для побудови стовпчастої діаграми величини, що порівнюють, зображують у вигляді стовпчиків, величина яких або дорівнює даним величинам, або пропорційна до них.

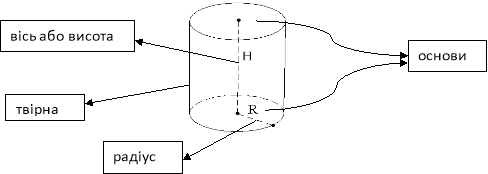
Циліндр можна утворити, якщо обертати прямокутник навколо однієї сторони.

Бічна поверхня циліндра – це поверхня, яку описує твірна під час обертання.

Повна поверхня циліндра = бічна поверхня + дві площі основи.

 

 

 

 

 

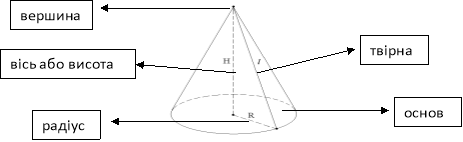
Конус можна утворити, якщо обертати прямокутний трикутник навколо однієї сторони, що утворює кут 90.

Бічна поверхня конуса – це поверхня, яку описує твірна під час обертання.

Повна поверхня конуса = бічна поверхня + площа

основи.

Куля – це обертання круга навколо діаметра.

Сфера – це поверхня кулі.

 

 

 

 

 

 

 

 

 

Тіла обертання – циліндр, конус, куля.

"Основоположник математичної культури нашого народу", - так сказав про Володимира Левицького академік Михайло Кравчук. Великою заслугою    В. Левицького було те, що він зібрав і впорядкував матеріали з української математичної термінології, що була надрукована в 1903 р. Основною ділянкою наукової роботи професора В. Левицького була теорія аналітичних функцій. Він займався також геометрією, алгеброю, диференціальними рівняннями та історією математики. Багато уваги приділяв теоретичній фізиці та астрономії.

ЗАДАЧІ

1. Після збору врожаю зернових культур з'ясувалося, що 50% усього врожаю становить пшениця, 15% — жито, 10% — овес і 25% — ячмінь. Побудувати стовпчасту та кругову діаграми розподілу врожаю зернових за видами культур.
2. Побудуйте стовпчасту діаграму, користуючись даними про тривалість життя деяких тварин: шимпанзе — 60 років, кінь — 20 років, верблюд — 25 років, крокодил — 40 років.
3. Лікарі рекомендують добову потребу в їжі розподілити на чотири частини: перший сніданок — 25%, другий сніданок — 15%, обід — 45%, вечеря — 15%. Побудуйте стовпчасту та кругову діаграми розподілу добової норми їжі.
4.  Побудуйте стовпчасту та кругову діаграми розподілу площ приміщень трикімнатної квартири, якщо площа кухні становить 15% площі квартири, спальні — 20%, дитячої кімнати — 15%, вітальні — 30%, передпокою — 10%, інших приміщень — 10%.
5. Діаметр отвору труби дорівнює 40 см, а товщина її стінок — 2 см. Чи вистачить 2,5 кг фарби, щоб пофарбувати зовні 10 м цієї труби, якщо на 1 м² її поверхні витрачається 200 г фарби?
6. Діаметр земної кулі приблизно дорівнює            12,7 тис. км. Знайдіть радіус Землі та довжину екватора.
7. Земну кулю стягнули обручем уздовж екватора. Потім збільшили довжину обруча на 1 м. Чи зможе кіт пролізти в утворену щілину?

 

М. Кравчук - автор понад 180 робіт, в тому числі 10 книг із різних розділів математики (алгебра і теорія чисел, теорія функцій дійсної і комплексної змінних, теорія диференціальних та інтегральних рівнянь, теорія ймовірностей і математична статистика, історія математики тощо.) Ці наукові праці увійшли до скарбниці світової науки. Тепер існують на сторінках наукових досліджень многочлени Кравчука, моменти Кравчука, осцилятори Кравчука. А ось від 2001 р., завдяки пошукам Івана Качановського, українського науковця зі США, виявилося, що наукові твори М. Кравчука прислужилися і до винаходу першого в світі електронного комп'ютера!

ДОДАТНІ ТА ВІД’ЄМНІ ЧИСЛА. ЧИСЛО 0.

КООРДИНАТНА ПРЯМА

 

 

Числа зі знаком «+» називають додатними.

Числа зі знаком «-» називають від’ємними.

Число 0 відділяє додатні числа від від’ємних.

0 – ні від’ємне, ні додатне.

Увага! Будь-яке натуральне число є додатним.

Застосування:

•       географія
•       мореплавство;
•       картографія;
•       геологія;
•       фізика;
•       астрономія;
•       інженерія;
•      медицина.

від’ємні числа                                         додатні числа

                С               О   А        В

                -3              0     1        3                     х

точка  О – початок відліку;

ОА – одиничний відрізок.

Координатна пряма – це пряма з вибраним на ній початком відліку, одиничним відрізком і вказаним додатним напрямом.

Координата точки – число, яке показує положення точки на координатній прямій.

О (0);   А (1);  В (3);   С (-3).

Увага!Кожній точці на координатній прямій відповідає єдина координата.

 

 

 

 

 

ЗАДАЧІ

1. Села А, В, С і В розташовані на прямолінійному шляху, що йде з півночі на південь. Відомо, що село А розташоване південніше від села В на        12 км, село С — північніше від села В на 6 км, село В — південніше від села С на 10 км. Із села   В у південному напрямі виїхав велосипедист і, проїхавши 6 км, зупинився. Чи проїхав велосипедист якесь із названих сіл? Вкажіть положення велосипедиста відносно сіл А та В.
2. Однією трасою, але у протилежних напрямах, їдуть автомобіль зі швидкістю 72 км/год і мотоцикліст зі швидкістю 48 км/год. У даний момент відстань між ними дорівнює 24 км. Якою може бути відстань між автомобілем і мотоциклістом через 10 хв?
3. Протягом дня равлик відповз від гілки вгору по дереву на 32 см, а протягом ночі опустився на:      а) 23 см; б) 41 см. На скільки сантиметрів від гілки і в якому напрямі від неї перемістився равлик протягомдоби?
4. Підводний човен спочатку плив на глибині 250 м, далі опустився ще на 300 м, а потім піднявся на 350 м. На якій глибині опинився підводний човен?

 

МОДУЛЬ ЧИСЛА

ЦІЛІ ЧИСЛА. РАЦІОНАЛЬНІ ЧИСЛА

 

                           А            О             В

                                  -3              0  1         3                     Х

Модуль числа – це відстань від початку відліку до точки, яка зображує це число.

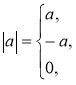
Протилежні числа – числа, які відрізняються один  від одного лише знаком, але мають рівні модулі.

5 і -5;   4 і -4;   а і –а;   0 – протилежне самому собі

Властивості модуля числа:

1. Модулем додатного числа і числа нуль є саме число.
2. Модулем від’ємного числа є протилежне йому додатне число.
3. Модулем будь-якого числа завжди додатне або нуль.
4. Протилежні числа мають рівні модулі.

 

Натуральні числа – числа, які використовуються для лічби предметів.

N = 1; 2; 3; 4;…

Цілі числа – натуральні числа, протилежні їм числа і число 0.

Z = {… -3; -2; -1; 0; 1; 2; 3; …}

Раціональні числа – цілі числа, дробові і число 0.

Позначають Q.

34;   2,5;    -54;  -5,3;    0 – раціональні числа.

 

ПОРІВНЯННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ.

ДОДАВАННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ

 

Правила:

1. З двох чисел більше лежить на координатній прямій правіше, а менше – лівіше.

                               А       О           В

                       -3    -2       0            3                     Х

-2 <3;    3 >-2.

2. Додатне число більше нуля.3 > 0
3. Від’ємне число менше нуля.-2 < 0
4. Додатне число більше за від’ємне.3 > -2
5. З двох від’ємних чисел більше те, у якого модуль менший.

-4 < -2, бо        

Увага!

Якщо число додатне, то записують:

Якщо число від’ємне, то записують:

Якщо число недодатне, то записують:

Якщо число невід’ємне, то записують:

Правила:

1. Сумою двох додатних чисел є додатне число.
2. а) Сумою двох від’ємних чисел є число від’ємне, модуль якого дорівнює сумі модулів доданків.

б) Щоб додати два від’ємні числа, треба додати їх модулі і в результаті поставити знак «–».

-3 + (-2) = -5

3. Щоб додати два числа з різними знаками, треба від більшого модуля відняти менший і в результаті поставити знак того доданка, модуль якого більший.

-5 + 3 = -2;           4 + (-2) = 2.

4. Сума двох протилежних чисел дорівнює нулю.

5 + (-5) = 0

Закони додавання

   Переставний                              Сполучний

 

 

 

 

 

 

 

 

 

ЗАДАЧІ

1. У касі було 5000 грн. Упродовж дня касир кілька разів видавав і приймав гроші, роблячи записи:

-10 грн, -300 грн, 460 грн, 530 грн, -1270 грн,           -650 грн. Скільки грошей залишилося в касі наприкінці дня?

2. Перед початком роботи водолаз опустився до позначки -34 м. Виконуючи роботу, він змінював глибину занурення на 6 м, 12 м, -17 м, -3 м, 20 м,   -5 м. На якій глибині опинився водолаз після закінчення роботи?
3. За перший день рівень води в річці змінився на      -9 см, за другий — на -8 см, а за третій — на           -6,5 см. На скільки сантиметрів змінився рівень води за три дні?
4. Протягом першої половини дня температура повітря змінилась на -1,5°С, а протягом другої — на -3,5°С. На скільки градусів змінилась температура повітря протягом дня?
5. Опівдні температура повітря була 2°С, до вечора вона змінилась на -4°С. Якою стала температура повітря ввечері?

 

 

ВІДНІМАННЯ  РАЦІОНАЛЬНИХ ЧИСЕЛ

 

Правило 1

Щоб від одного числа відняти інше, досить до зменшуваного додати число, протилежне від’ємнику.

 

 

- 10 – 2 = - 10 + (- 2) = - 12;

10 – 12 = 10 + (- 12) = -2;

Довжина відрізка

А (-2);  В (4)

                                     А       О               В

 

               -2       0                4                 Х

АВ = 4 – (-2) = 6

Правило 2

Щоб знайти довжину відрізка на координатній прямій, потрібно від координати його правого кінця відняти координату лівого кінця.

 

Архімед за допомогою математичних розрахунків сконстроював силу-силенну всіляких механізмів, що допомогли у війні проти римлян при облозі Сіракуз до такої міри ,що Марцелло вимушений був сказати: «треба припинити війну проти Геометра». Пізніше тільки зрада допомогла римлянам ввійти до Сіракуз. Через давність років історія життя Архімеда тісно переплелася з легендами про нього. Вони почали виникати ще за життя науковця, приводом для них служили його вражаючі винаходи, які здійснювали приголомшливу дію на сучасників.

 

ЗАДАЧІ

1. Мертве море знаходиться на висоті -425 м відносно рівня Світового океану. Каспійське море, що є найбільшим у світі озером, знаходиться на висоті -28 м відносно рівня Світового океану. На скільки метрів рівень Каспійського моря вищий за рівень Мертвого моря?
2. Абсолютний максимум температури повітря        42 °С в Україні був зафіксований у серпні 2010 р. у Луганській області. Абсолютний мінімум температури -43 °С був зафіксований у січні 1923 р. ВКарпатах. Знайдіть різницю абсолютних максимуму і мінімуму температур.
3. Найнижча температура повітря, яку було зафіксовано в пустелі Сахара, дорівнює -5°С, а найвища — 55,4°С. Визначте різницю між найвищою і найнижчою температурами повітря, зафіксованими в Сахарі.
4. Ртуть плавиться при температурі -38,9 °С, а мідь — при температурі 1083,4°С. На скільки градусів температура плавлення міді вища за температуру плавлення ртуті?
5. Найнижча зафіксована на поверхні Землі температура дорівнювала -89,2 °С, що на 70,8 °С вище за найнижчу температуру, виміряну на поверхні Місяця. Чому дорівнює найнижча температура, зафіксована на Місяці

МНОЖЕННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ

Правило 1.  Добуток двох чисел з різними знаками є від’ємним числом, модуль добутку дорівнює добутку модулів множників.

 Щоб знайти добуток двох чисел з різними знаками, досить перемножити їх модулі і поставити в результаті знак «–».

 -5  3 = - 15;       3   (-5) = - 15. 

Правило 2. Добуток двох від’ємних чисел є додатним числом, модуль добутку дорівнює добутку модулів множників.

 Щоб знайти добуток двох від’ємних чисел, досить перемножити їх модулі.

-5  (- 3) = 15.

Правило 3

 Якщо число а – додатне, від’ємне або 0, то

а  0 = 0.

 

 

Друг мого друга – мій друг	(+1)  (+1)= +1
Ворог мого друга – мій ворог	(-1)  (+1)= -1
Ворог мого ворога – мій друг	(-1)  (-1)= +1
Друг мого ворога – мій ворог	(+1)  (-1)= -1

Розподільна властивість: для будь-яких раціональних чисел a,bі с справджується рівність:

(a+ b) с = ас +bс

Заміна виразу (a+ b) с на вираз ас +bс називають розкриттям дужок.

-5  (2а + 3b) = -10а – 15b.

Заміна виразу ас +bс на вираз (a + b) с називають винесенням спільного множника за дужки.

  3а – 9а + 2а = -4а.

-4 – коефіцієнт

Подібні доданки – мають однакову буквену частину і відрізняються один від одного лише коефіцієнтами.

 

Правило. Щоб звести подібні доданки, потрібно додати їх коефіцієнти і результат помножити на спільну буквену частину.

4а – 5b + 3 – 2а – 3b= 2а – 8b + 3.

 

Правила розкриття дужок:

1. Якщо перед дужками стоїть знак «+», то потрібно опустити дужки і знак «+», що стоїть перед ними, та записати всі доданки, які були в дужках, зі своїми знаками.
2. Якщо перед дужки стоїть знак «-», то потрібно опустити дужки і знак «-», що стоїть перед ними, і записати всі доданки, які були в дужках, із протилежними  знаками.

ДІЛЕННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ

 

Правило 1

Частка  двох чисел з різними знаками є число від’ємне.

 Щоб знайти модуль частки двох чисел з різними знаками, потрібно модуль діленого поділити на модуль дільника.

-15 : 3 = - 5;   бо    -5  3= - 15.

Правило 2

Частка двох від’ємних чисел є додатним числом.

 Щоб знайти модуль частки, потрібно модуль діленого поділити на модуль дільника.

-15 : (- 3) = 5,    бо    5  (-3) = - 15.

Правило 3

 Якщо число а – раціональне число, то

 

 

 

 

 

 

РІВНЯННЯ. ОСНОВНІ ВЛАСТИВОСТІ РІВНЯНЬ. ЗАСТОСУВАННЯ РІВНЯНЬ ДО РОЗВ’ЯЗУВАННЯ ЗАДАЧ

 

Рівняння – рівність, яка містить невідоме, значення якого треба знайти.

Корінь рівняння – значення невідомого, при якому рівняння перетворюється на правильну числову рівність.

Розв’язати рівняння означає знайти всі його корені або показати, що їх немає.

Властивості рівнянь:

1. Якщо до обох частин рівняння додати або відняти одне й те саме число, то рівняння не зміниться.
2. Доданки можна переносити з однієї частини рівняння в іншу, змінюючи при цьому їх знаки на протилежні.
3. Якщо обидві частини рівняння помножити або поділити на одне й те саме число, відмінне від нуля, то рівняння не зміниться.

 

Приклад 1.  4х + 3 = 6х – 5;   

    4х - 6х = - 5 – 3;  

- 2х = - 8;     

х = - 8 : (- 2);   

х = 4.     

Перевірка: Ліва частина: 4  4 + 3 = 16 + 3 = 19.

            Права частина: 6  4 – 5 = 24 – 5 = 19.

Відповідь: 4.

Приклад 2.           5(2х - 1) = 4х – 23;

10х – 5 = 4х – 23;

10х - 4х = - 23 + 5;

6х = - 18;

х = - 18 :  6;

х = - 3.

Перевірка:

            Ліва частина: 5 (2  (- 3) – 1) = 5 (-6 – 1) = 5  (- 7) = - 35.

Права частина: 4  (- 3) – 23 = - 12 – 23 = -35.

Відповідь: - 3.

Задача 1. У двох бідонах є 36 л молока, до того ж, у першому бідоні молока в 1,4 разу більше, ніж у другому. Скільки молока в кожному бідоні?

Нехай х л – молока в другому бідоні, а 1,4х л – молока в першому бідоні. Тоді за умовою задачі будемо мати рівняння:

х + 1,4х = 36;

2,4х = 36;

х = 36 : 2,4;

х = 15.

1,4  15 = 21 (л).

Відповідь: 21 л, 15 л.

Задача 2. На трьох полицях стоїть 129 книжок, до того ж, на другій полиці на 15 книжок більше, ніж на першій, а на третій – на 12 книжок менше, ніж на першій. Скільки книжок стоїть на кожній полиці?

Нехай х –  книжок на першій полиці, (х + 15) – книжок на другій полиці, а (х - 12) – на третій полиці. Тоді за умовою задачі будемо мати рівняння:

х + (х + 15) + (х - 12) = 129;

х + х + 15 + х – 12 = 129;

3х + 3 = 129;

3х = 129 - 3;

3х = 126;

х = 126 : 3;

х = 42.

42 + 15 = 57 (книжок);  42 – 12 = 30 (книжок).

Перевірка: 42 + 57 + 30 = 129 (книжок).

Відповідь: 42, 57 і 30 книжок.

Давньогрецький математик Піфагор брав участь у кулачному бою на 58 Олімпіаді, яка проходила в 548 р. до н. е. Він був чемпіоном з цього виду спорту і утримував цей титул ще на кількох олімпіадах. Чи знаєте ви, що теорему Піфагора називали «ослячим мостом»? Учнів, що запам’ятовували теорему без розуміння, називали віслюками, оскільки вони не могли перейти через міст — теорему Піфагора.

ЗАДАЧІ

1. Аладдін купив вершкове морозиво по 12 драхм за порцію і шоколадне — по 18 драхм. Скільки порцій кожного виду морозива придбав Аладдін, якщо всього він купив 24 порції, заплативши за всю покупку 372 драхми?
2. Карлсон купив 16 тістечок по 10 крон і по            16 крон, заплативши всього 202 крони. Скільки тістечок кожного виду купив Карлсон?
3. Двом школам виділили на ремонт однакову суму грошей. Коли для першої школи придбали будівельні матеріали вартістю 60000 грн, а для другої — вартістю 30000 грн, то в розпорядженні другої школи залишилося грошей в 1,5 раза більше, ніж у першої. Скільки гривень було виділено кожній школі?
4. У дві цистерни для поливання городу налили однакову кількість води. Коли з першої цистерни використали 47 л води, а з другої — 23 л, то в першій залишилося в 3 рази менше води, ніж у другій. Скільки літрів води було в кожній цистерні спочатку?
5. У Сашка було в 5 разів більше грошей, ніж у Оленки. Коли Сашко купив книжку за 27 грн, а Оленка — ляльку за 8 грн, то в Оленки залишилося на 33 грн менше, ніж у Сашка. Скільки грошей було в кожного з них спочатку?
6. У першому контейнері було в 4 рази більше вугілля, ніж у другому. Коли з першого контейнера взяли 210 кг вугілля, а з другого —    10 кг, то в другому залишилося на 20 кг більше, ніж у першому. Скільки кілограмів вугілля було в кожному контейнері спочатку?
7. З одного міста до другого виїхав автомобіль зі швидкістю 65 км/год, а через 2 год після цього з другого міста назустріч йому виїхав інший автомобіль зі швидкістю 75 км/год. Знайдіть час, протягом якого був у дорозі кожний автомобіль до моменту зустрічі, якщо відстань між містами дорівнює 690 км.
8. Човен плив 1,4 год за течією річки і 1,7 год проти течії. Шлях, який проплив човен за течією, виявився на 2,2 км коротшим за шлях, який він проплив проти течії. Знайдіть швидкість течії річки, якщо швидкість човна в стоячій воді становить 28 км/год.
9. Готуючись до іспиту, учень планував щодня розв’язувати 12 задач. Проте він розв’язував щодня на 4 задачі більше і вже за 3 дні до іспиту йому залишилося розв’язати 8 задач. Скільки днів планував учень готуватися до іспиту?
10. У великому бідоні утричі більше молока, ніж у малому. Коли у великий бідон долили 6 л молока, а в малий — 7 л, то у великому бідоні молока стало удвічі більше, ніж у малому. Скільки молока було в кожному бідоні спочатку?
11. У двох корзинах було порівну яблук. Після того, як із першої корзини взяли 50 яблук, а з другої — 90, у першій корзині яблук стало втричі більше, ніж у другій. Скільки яблук було в кожній корзині спочатку?
12. На виставку привезли котів сибірської, ангорської, перської та сіамської порід. Ангорських котів було вдвічі більше, ніж перських, сибірських — утричі більше, ніж ангорських, а сіамських на 4 менше, ніж ангорських. Скільки котів кожної породи було на виставці, якщо усього їх було 51?
13. У першій цистерні було 900 л води, а в другій — 700 л. Коли з другої цистерни взяли води вдвічі більше, ніж з першої, то в першій залишилося води втричі більше, ніж у другій. Скільки літрів води взяли з кожної цистерни?
14. У першому контейнері було 60 кг яблук, а в другому — 100 кг. Коли з другого контейнера продали в 4 рази більше яблук, ніж з першого, то в першому залишилося у 2 рази більше яблук, ніж у другому. Скільки кілограмів яблук продали з кожного контейнера?
15. Щохвилини в першу діжку з крана наливалося 3 л води, а в другу з іншого крана — 2 л. О 12 год у першій діжці було 21 л води, а в другій — 54 л.

 З ’ясуйте, о котрій годині в першій діжці було в 4 рази менше води, ніж у другій.

ПАРАЛЕЛЬНІ ТА ПЕРПЕНДИКУЛЯРНІ ПРЯМІ

 

             а

 

             b

 

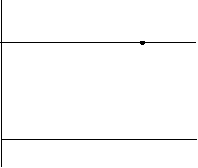
Дві прямі називають паралельними, якщо вони не перетинаються і лежать в одній площині.

а  b

Властивість:через кожну точку, яка не належить даній прямій, можна провести тільки одну пряму, паралельну даній.

     с     А

              b

 

      а

 

              В

 

 

               C          D

    

                              A

 

 

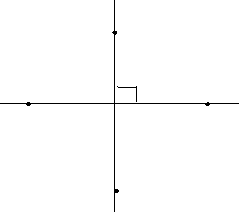
Дві прямі називають перпендикулярними, якщо вони  перетинаються під прямим кутом.

ABCD

 

Властивість:через кожну точку прямої можна провести перпендикулярну до неї пряму і до того ж тільки одну.                       b

 

 

 

                                      А

 

Михайлу Остроградському належить одне з найпочесніших місць в історії світової математичної науки. Непересічний талант, сміливий і гострий розум, висока математична ерудиція, знання сучасного природознавства дозволили Михайлу Васильовичу зробити першорядні відкриття в багатьох галузях математики і механіки. Діапазон наукової творчості Остроградського надзвичайно широкий: диференціальне та інтегральне числення, алгебра, теорія чисел, диференціальна геометрія, теорія ймовірностей, математична фізика, варіаційне числення, аналітична механіка, теорія удару, балістика тощо.
 

 

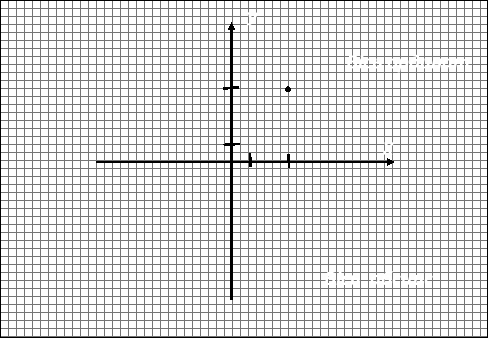
КООРДИНАТНА ПЛОЩИНА

 

 

 

 

 

 

 

 

 

 

Прямокутна система координат – дві взаємно перпендикулярні прямі з вибраними одиничними відрізками і напрямами.

ОХОУ;

точка О – початок відліку

ОХ – вісь абсцис

ОУ – вісь ординат

Координатна площина – площина, на якій задано прямокутну систему координат.

Координати точки показує положення точки на координатній площині.

А (3; 4) – координати точки.

Абсциса точки – перша координата

Ордината точки – друга координата

Увага!

Якщо точка лежить на абсцисі, то її ордината дорівнює нулю.

Якщо точка лежить на ординаті, то її абсциса дорівнює нулю.

Осі координат розбивають площину на 4 частини, які називають координатними чвертями.

 

 

                      ІІ             у       І

    чверть                 чверть

     (-; +)                    (+; +)

 

                                     О                      х

    ІІІ        ІV

    чверть                  чверть       

                        (-; -)                  (+; -)

Юрій Львович Далецький – всесвітньо відомий математик, гордість вітчизняної науки. Основні праці вченого присвячені дослідженню сучасних проблем математичного аналізу, теорії ймовірностей, теорії диференціальних рівнянь і математичної фізики.  Ним написано біля  200 наукових праць, серед них значну частину складають ґрунтовні статті та монографії, які перекладено англійською мовою. До скарбниці світової літератури з математики і теоретичної фізики увійшла важлива формула Далецького-Троттера про мультиплікативне представлення еволюційного інтеграла.  За вагомий внесок у розвиток національної освіти академіку НАН України  Ю.Л.Далецькому присвоєно почесне звання - Заслужений діяч науки і техніки України.

 

 

 

 

 

 

Зміст

Дільники і кратні натурального числа.

Прості числа

Ознаки подільності на 2, 10, 5

Ознаки подільності на 9, 3

Розкладання чисел на прості множники. Найбільший спільний дільник

Кратні натурального числа.

Найменше спільне кратне

Основна властивість дробу.

Скорочення дробу

Зведення дробів до спільного знаменника.   Порівняння дробів

Додавання і віднімання дробів з різними знаменниками

Множення звичайних дробів

Ділення дробів.

Знаходження числа за його дробом

Відношення та його властивості.

Пряма та обернена пропорційні залежності.  Поділ числа в даному відношенні. Масштаб

Ймовірність випадкової події

Відсоткові розрахунки

Коло. Довжина кола.

Круг. Площа круга

Діаграми.

Циліндр. Конус. Куля

Додатні та від’ємні числа. Число 0.

Координатна пряма

Модуль числа

Цілі числа. Раціональні числа

Порівняння раціональних чисел.

Додавання раціональних чисел

Віднімання  раціональних чисел

Множення раціональних чисел

Ділення раціональних чисел

Рівняння. Основні властивості рівнянь.

Застосування рівнянь до розв’язування задач

Пралельні та перпендикулярні прямі

Координатна площина

 

Розв'язування задач є найхарактернішим і найспецифічнішим різновидом вільного мислення. (В. Джеймс)

За допомогою логіки доводять, за допомогою інтуїції винаходять. (А. Пуанкаре)

 

 

 

 

Жодна інша наука не навчає так ясно розуміти

гармонію природи, як математика…

                                              (П. Карус)

 

Математика і поезія – це… вираз тієї самої сили уяви, тільки в першому разі уява повернена до голови, а в другому – до серця.

(Т. Хілл)