Методична розробка електронного навчально-методичного посібника "Конус"

Міністерство освіти і науки України

Вільногірський фаховий коледж Національної металургійної академії України

 

 

 

 

 

ЕЛЕКТРОННИЙ НАВЧАЛЬНО-МЕТОДИЧНИЙ ПОСІБНИК ТЕМИ

«КОНУС»

для здобувачів освіти спеціальностей 151 Автоматизація та комп’ютерно-                                                                                    інтегровані технології; 133 Галузеве машинобудування; 136 Металургія

 

 

 

 

Гадик Вікторія Анатоліївна

 

 

 

 

 

 

Вільногірськ

2020 р.

Укладач: Гадик В.А., викладач вищої категорії.

Рецензент: Гибало Т.Г., викладач вищої категорії, викладач-методист, голова циклової комісії загальноосвітніх та загально-технічних дисциплін Вільногірського коледжу НМетАУ.

 

 

Розглянуто і схвалено цикловою комісією загальноосвітніх та загально-технічних дисциплін Вільногірського фахового коледжу НМетАУ Протокол № 4 від 09.12.2020 р.

Розглянуто і схвалено методичною радою Вільногірського фахового коледжу НМетАУ Протокол № 5 від 06.01.2021 р.

 

 

Анотація: даний посібник призначений для дидактичного забезпечення самостійного вивчення теми «Конус» розділу  курсу геометрії . До складу посібника входять електронний робочий зошит, навчальний посібник, тестові завдання, довідник розв‘язування задач з теми, збірка задач для самостійного виконання. Рекомендується: для викладачів математики – як методичний посібник, для здобувачів освіти – як навчальний посібник.

(https://cutt.ly/gjfbxJK)

 

 

 

 

 

 

ЗМІСТ

Вступ……………………………………………………………………………….4 

1 Навчальний посібник

   1.1 Теоретичний матеріал……………………....................................................7

   1.2  Приклади розв‘язування задач з теми…………………………………….9

   1.3 Тренувальні вправи……………………………………………………..…10

2 Тестові завдання…………………………………………………………...…..11

3 Збірник задач………………………………………………………………...…27

4 Електронний робочий зошит.............................................................................29

5 Висновки…………………………………………………………………….…32

6 Бібліографічний опис……………………………………………………….…33

 

             

ВСТУП

Електронний навчально-методичний посібник, що пропонується, містить необхідні засоби навчання  для самостійного вивчення теми «Конус» розділу  курсу геометрії. Посібник може використовуватися при вивченні курсу геометрії за програмою академічного, профільного рівнів.

 Використовуючи посібник, викладач зможе методично забезпечити самостійну роботу здобувачів освіти в аудиторії і вдома. Оскільки посібник звільняє викладача від пошуку потрібного навчального матеріалу, у викладача з’являється час для творчого пошуку та консультацій для здобувачів освіти, які працюють над проектами, тощо.

Пріоритетними підходами до розробки предметного змісту посібника є такі:

- орієнтація змісту освіти на розвиток інтелектуальної сфери,

  формування позитивної мотивації, самостійності здобувачів освіти;

- відповідність предметного змісту структурі державного

            загальноосвітнього стандарту;

- розвиток рефлексивної здатності, опанування способів саморегуляції,

  самовдосконалення та самоактуалізації;

- посилення соціальної та практичної спрямованості змісту освіти;

- оволодіння методами наукового пізнання.

Даний посібник є складовою частиною інформаційно-праксіологічного середовища для вивчення розділу курсу геометрії.

Інформаційно-праксіологічне середовище навчального призначення                         в посібнику з методичним і технологічним супроводом розглядається як цільове, процесуальне й інструментальне забезпечення навчання, виховання й розвитку особистості, яке створюється, перш за все, з метою вирішення головного завдання випереджаючої освіти - формування самоосвітньої

компетентності.

Створення навчальних посібників з використанням інформаційно-праксеологічних середовищ  дозволяє створити освітні ресурси дистанційного навчання, вирішити завдання інтеграції освітнього процесу коледжа в інформаційно-освітній простір; створити колекції освітніх ресурсів та тематичні освітні веб-сайти по предметах, підвищити дидактичний потенціал освітнього процесу.

Обов'язкові умови:

• тестування системи на предмет коректної інтерпретації предметної

          області, методики подання навчального матеріалу;

• естетичне сприйняття інтерфейсу;
• апробація системи на реальних здобувачів освіти з метою збору

          статистичних даних, результат обробки яких дійсно підтвердить

          підвищення ефективності навчання.

Середовище повинне містити розгорнуту базу знань, системно організовані блоки навчальної інформації й контролю, модель здобувача освіти й можливість організовувати для нього індивідуальний маршрут. Вихідною позицією процесу навчання є формування базового тезауруса предметної області. Тому базу знань в освітнім середовищі формують у формі модулів навчальної дисципліни, організованих у вигляді відеокліпів, слайдів, текстових фрагментів й інших мультимедійних форм подання інформації.

Даний електронний навчально-методичний посібник передбачає вивчення нового матеріалу колективно, під керівництвом викладача, або індивідуально на уроці (вдома). Посібник містить теоретичний матеріал, передбачений програмою; приклади розв’язування задач; тренувальні вправи; контролюючі завдання. Посібник розрахований на різнорівневе навчання: академічний рівень, профільний рівень. В залежності від можливостей та бажання здобувача освіти, пропонуються завдання поглибленого рівня та  завдання математичних конкурсів та олімпіад.

При вивченні теми, здобувач освіти повинен навчитись:

•      користуватися властивостями конуса;
•      будувати перерізи та обчислювати їх елементи;
•      знаходити окремі елементи конуса;
•      використовувати формули для обчислення об’єму;
•      застосовувати властивості об’ємів тіл для розв’язування задач.

 

 

 

 

 

 

 

 

 

 

 

1 НАВЧАЛЬНИЙ ПОСІБНИК

        1.1 Теоретичний матеріал

1)  Приклади конусних поверхонь:    

             

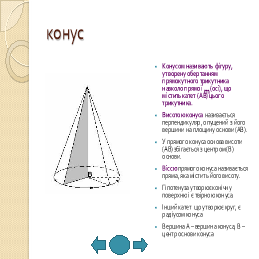
2)  Означення та елементи конуса:

          

          

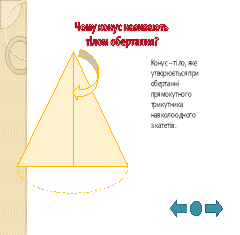
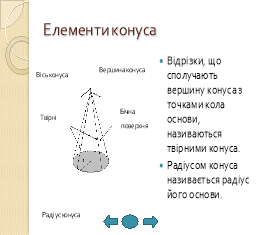
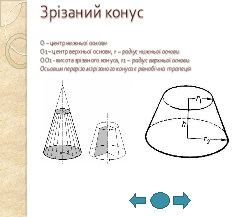
3) Перерізи конуса:   

   

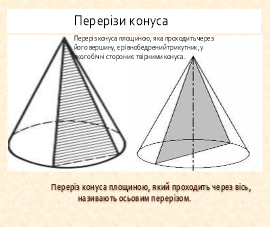
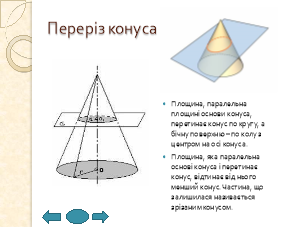
4) Площа бічної та повної поверхонь:

     

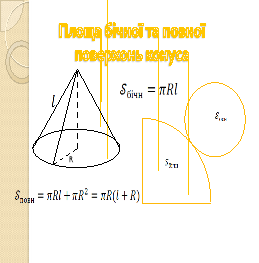
5) Об’єм конуса

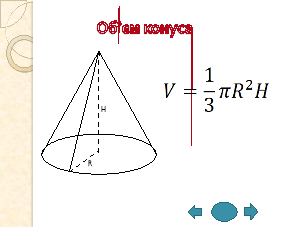
6) Комбінації конуса

      

 

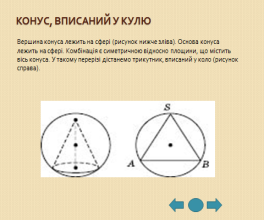
          1.2 Приклади розв’язування задач

     

    

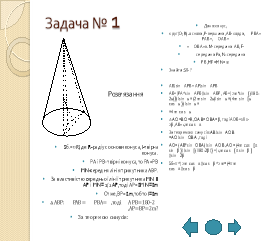
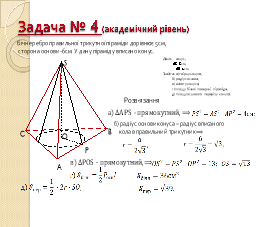
        1.3 Тренувальні вправи

    

     

          

          

 

2 ТЕСТОВІ ЗАВДАННЯ

Мета цього тесту — перевірити, чи вміє здобувач освіти:

користуватися властивостями конуса, зрізаного конуса;

будувати перерізи та обчислювати їх елементи;

знаходити окремі елементи конуса, зрізаного конуса.

 

Тестові завдання містять варіанти з відповідями – для викладача

 і без відповідей – для здобувача освіти.

Варіант 1.

1. Дано зрізаний конус з віссю OO_1.  AA₁B₁B — переріз конуса площиною, що проходить через дві твірні і не проходить через вісь. Виберіть правильне тверд­ження.

+1). A₁B₁ — хорда однієї з основ.

–2). A₁B₁ —  діаметр однієї з основ.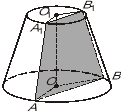

+3). Відрізок AA₁– більше висоти конуса.

–4). AA₁– висота конуса.

+5). AA₁ —  твірна зрізаного конуса.

–6). AA₁ < BB₁.

+7). A₁AB  <  90.

     –8). A₁AB = 90.

2. Дано прямий круговий конус, у якого радіус основи R і висота H. Позначте, які з наведених чотирьох тверджень правильні, а які — неправильні.

+1). Твірна більше висоти конуса.

–2). Твірна може дорівнювати висоті конуса.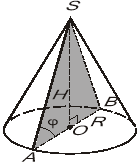

+3). Твірна більше радіуса основи конуса.

–4). Твірна може дорівнювати радіусу основи конуса.

+5). Твірна складає з площиною основи кут  такий, що .

–6). Твірна складає з площиною основи кут  такий, що .

+7). Площа осьового перерізу конуса дорівнює RH.

    –8). Площа осьового перерізу конуса дорівнює .

+1). Висота конуса дорівнює його радіусу.

–2). Висота конуса більше його радіуса.

+3). Твірна утворює з площиною основи кут 45.

–4). Твірна утворює з площиною основи кут більше 45.

+5). Твірна конуса дорівнює .

–6). Твірна конуса дорівнює .

+7). Відстань від центра основи конуса до твірної дорівнює половині твірної.

–8). Відстань від центра основи конуса до твірної менше половини твірної.

+1). Найбільшу площу не може мати осьовий переріз.

–2). Найбільшу площу має осьовий переріз.

+3). Найбільшу площу має переріз, який є прямокутним трикутником.

–4). Найбільшу площу має переріз, який не є прямокутним трикутником.

+5). Найбільша площа перерізу дорівнює .

–6).Найбільша площа перерізу дорівнює .

+7).Площа осьового перерізу конуса дорівнює .

–8).Найбільша площа перерізу конуса дорівнює .

Варіант 2

1. Дано прямий круговий конус з віссю OS. ASB — переріз конуса площиною, що проходить через вершину S і не проходить через вісь конуса. Виберіть правильне твердження.

+1). AS = SB.

–2). AS > SB.

+3). ASB — рівнобедрений трикутник.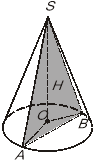

–4). ASB — не є рівнобедреним трикутником.

+5). SAB = SBA.

–6). SAB  SBA.

+7). AO + OB  >  AB.

–8). AO + OB = AB.

2. Конус з  радіусом основи R  і висотою H перетнули площиною, паралельною його основі на відстані h від вершини. Позначте, які з наведених чотирьох тверд­жень правильні, а які — неправильні.

+1). Площина відтинає конус, подібний даному.

–2). Площина відтинає конус рівний даному.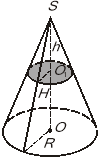

+3). Одна з отриманих частин є зрізаним конусом.

–4). Обидві отримані частини є зрізаними конусами.

+5). Радіус перерізу конуса менше радіуса основи.

–6). Радіус перерізу конуса дорівнює радіусу основи.

+7). Радіус перерізу конуса дорівнює .

–8). Радіус перерізу конуса дорівнює .

+1). Площини бічної грані піраміди і осьового перерізу конуса, які мають спільну твірну, взаємно перпендикулярні.

–2). Площини бічної грані піраміди і осьового перерізу конуса, які мають спільну твірну, не можуть бути взаємно перпендикулярними.

+3). Твірна конуса нахилена до площини основи під кутом 60.

–4). Твірна конуса нахилена до площини основи під кутом 30.

+5). Твірна конуса дорівнює 10 дм.

–6). Твірна конуса дорівнює 5 дм.

+7). Площа осьового перерізу конуса дорівнює 55дм² .

–8). Площа осьового перерізу конуса дорівнює 75дм² .

+1). Сума діаметрів двох основ конуса дорівнює a.

–2). Сума діаметрів двох основ конуса більше a.

+3). Висота зрізаного конуса дорівнює сумі радіусів основ конуса.

–4). Висота зрізаного конуса менше суми радіусів основ конуса.

+5). Твірна конуса дорівнює .

–6). Твірна конуса дорівнює .

+7). Діаметр меншої основи не може дорівнювати твірній конуса при будь-якому .

–8). Діаметр меншої основи може дорівнювати твірній конуса.

Варіант 3

1. Дано зрізаний конус з віссю OO₁, у якого AA₁B₁B — осьовий переріз. Виберіть правильне твердження.

+1). AA₁B₁B — рівнобічна трапеція.

–2). AA₁B₁B —прямокутник.

+3). A₁O₁O = 90.

–4). A₁O₁O < 90.

+5). AA₁ O₁O — прямокутна трапеція.

–6). AA₁ O₁O —  рівнобічна трапеція.

+7). Відрізок OO₁ дорівнює висоті конуса.

–8). Відрізок OO₁ менше висоти конуса.

2. При обертанні прямокутного трикутника навколо одного з катетів отримали прямий круговий конус. Позначте, які з наведених чотирьох тверджень правильні, а які — неправильні.

+1). Один з катетів дорівнює радіусу основи конуса.

–2).  Катети більше радіуса основи конуса.

+3). Кожний з катетів менше твірної.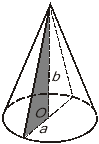

–4). Один з катетів дорівнює твірній.

+5). Гіпотенуза прямокутного трикутника дорівнює твірній.

–6). Гіпотенуза прямокутного трикутника більша твірної.

+7). Якщо a і b катети трикутника, то площа осьового перерізу конуса дорівнює ab.

    –8). Якщо a і b катети трикутника, то площа осьового перерізу конуса

           дорівнює 2ab

+1). Осьовим перерізом частини, яка є зрізаним конусом, є трапеція.

–2). Осьовим перерізом частини, яка є зрізаним конусом, є прямокутник.

+3). Радіуси перерізу і основи відносяться як h : H.

–4). Радіуси перерізу і основи відносяться як h : (H–h).

+5). Якщо , то твірні обох частин рівні.

–6). Якщо , то твірні обох частин відносяться як 1:4.

+7). Площа перерізу дорівнює .

–8). Площа перерізу менше .

+1). Основа піраміди —тупокутний трикутник.

–2). Основа піраміди — гострокутний трикутник.

+3). Бічні ребра піраміди рівні.

–4). Бічні ребра піраміди своєю проекцією на площину основи мають радіус кола, вписаного в основу.

+5). Основа висоти конуса не належить основі піраміди.

–6). Основа висоти конуса належить основі піраміди.

+7). Радіус основи конуса менше 10 см.

–8). Радіус основи конуса дорівнює 10 см.

Варіант 4

1. Дано прямий круговий конус з віссю OS. ASB — осьовий переріз конуса. Виберіть правильне твердження.

+1). AB — діаметр основи конуса.

–2). AB — радіус основи конуса.

+3). SB > SO.

–4). SB  SO.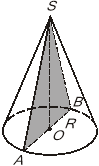

+5). SOA = 90.

–6). SOA > 90.

+7). AS = SB.

–8). AS > SB.

2. Прямий круговий зрізаний конус утворили обертанням прямокутної трапеції з гострим кутом  і прилеглою бічною стороною l навколо меншої бічної сторони. Позначте, які з наведених чотирьох тверджень правильні, а які — неправильні.

+1). Радіуси основ конуса дорівнюють основам трапеції.

–2). Радіуси основ конуса дорівнюють бічним сторонам трапеції.

+3). Твірна дорівнює більшій бічній стороні даної трапеції.

–4). Твірна дорівнює меншій бічній стороні даної трапеції.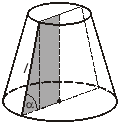

+5). Відстань від центра нижньої основи до твірної менше радіуса нижньої основи.

–6). Відстань від центра нижньої основи до твірної дорівнює радіусу нижньої основи.

+7). Висота конуса дорівнює lsin.

–8). Висота конуса дорівнює lcos.

+1). Радіуси перерізу і основи даного конуса відносяться як :.

–2). Радіуси перерізу і основи даного конуса відносяться як 1 : 2.

+3). Висота даного конуса відноситься до висоти отриманого повного конуса  як :  1.

–4). Висота даного конуса відноситься до висоти отриманого повного конуса  як 2 :  1.

+5). Площина перерізу відстоїть від вершини на .

–6). Площина перерізу відстоїть від вершини на .

+7). В отриманий зрізаний конус можна вписати правильну n-кутну зрізану піраміду, висота якої дорівнює .

+8). В отриманий зрізаний конус можна вписати правильну n-кутну зрізану піраміду, висота якої дорівнює .

+1). Осьовий переріз конуса є тупокутним трикутником.

–2). Осьовий переріз конуса є гострокутним трикутником.

+3). Площа осьового перерізу менша площі даного перерізу.

–4). Площа осьового перерізу більша площі даного перерізу.

+5). Площа даного перерізу дорівнює

–6). Площа даного перерізу дорівнює .

+7). Висота конуса дорівнює sin.

–8). Висота конуса дорівнює cos.

Варіант 1.

1. Дано зрізаний конус з віссю OO_1.  AA₁B₁B — переріз конуса площиною, що проходить через дві твірні і не проходить через вісь. Виберіть правильне тверд­ження.

1). A₁B₁ — хорда однієї з основ.

2). A₁B₁ —  діаметр однієї з основ.

3). Відрізок AA₁– більше висоти конуса.

4). AA₁– висота конуса.

5). AA₁ —  твірна зрізаного конуса.

6). AA₁ < BB₁.

7). A₁AB  <  90.

8). A₁AB = 90.

2. Дано прямий круговий конус, у якого радіус основи R і висота H. Позначте, які з наведених чотирьох тверджень правильні, а які — неправильні.

1). Твірна більше висоти конуса.

2). Твірна може дорівнювати висоті конуса.

3). Твірна більше радіуса основи конуса.

4). Твірна може дорівнювати радіусу основи конуса.

5). Твірна складає з площиною основи кут  такий, що .

6). Твірна складає з площиною основи кут  такий, що .

7). Площа осьового перерізу конуса дорівнює RH.

     8). Площа осьового перерізу конуса дорівнює .

1). Висота конуса дорівнює його радіусу.

2). Висота конуса більше його радіуса.

3). Твірна утворює з площиною основи кут 45.

4). Твірна утворює з площиною основи кут більше 45.

5). Твірна конуса дорівнює .

6). Твірна конуса дорівнює .

7). Відстань від центра основи конуса до твірної дорівнює половині твірної.

8). Відстань від центра основи конуса до твірної менше половини твірної.

1). Найбільшу площу не може мати осьовий переріз.

2). Найбільшу площу має осьовий переріз.

3). Найбільшу площу має переріз, який є прямокутним трикутником.

4). Найбільшу площу має переріз, який не є прямокутним трикутником.

5). Найбільша площа перерізу дорівнює .

6).Найбільша площа перерізу дорівнює .

7).Площа осьового перерізу конуса дорівнює .

8).Найбільша площа перерізу конуса дорівнює .

Варіант 2

1. Дано прямий круговий конус з віссю OS. ASB — переріз конуса площиною, що проходить через вершину S і не проходить через вісь конуса. Виберіть правильне твердження.

1). AS = SB.

2). AS > SB.

3). ASB — рівнобедрений трикутник.

4). ASB — не є рівнобедреним трикутником.

5). SAB = SBA.

6). SAB  SBA.

7). AO + OB  >  AB.

8). AO + OB = AB.

2. Конус з  радіусом основи R  і висотою H перетнули площиною, паралельною його основі на відстані h від вершини. Позначте, які з наведених чотирьох тверд­жень правильні, а які — неправильні.

1). Площина відтинає конус, подібний даному.

2). Площина відтинає конус рівний даному.

3). Одна з отриманих частин є зрізаним конусом.

4). Обидві отримані частини є зрізаними конусами.

5). Радіус перерізу конуса менше радіуса основи.

    6). Радіус перерізу конуса дорівнює радіусу основи.

7). Радіус перерізу конуса дорівнює .

8). Радіус перерізу конуса дорівнює .

1). Площини бічної грані піраміди і осьового перерізу конуса, які мають спільну твірну, взаємно перпендикулярні.

2). Площини бічної грані піраміди і осьового перерізу конуса, які мають спільну твірну, не можуть бути взаємно перпендикулярними.

3). Твірна конуса нахилена до площини основи під кутом 60.

4). Твірна конуса нахилена до площини основи під кутом 30.

5). Твірна конуса дорівнює 10 дм.

6). Твірна конуса дорівнює 5 дм.

7). Площа осьового перерізу конуса дорівнює 55дм² .

 8). Площа осьового перерізу конуса дорівнює 75дм² .

1). Сума діаметрів двох основ конуса дорівнює a.

2). Сума діаметрів двох основ конуса більше a.

3). Висота зрізаного конуса дорівнює сумі радіусів основ конуса.

4). Висота зрізаного конуса менше суми радіусів основ конуса.

5). Твірна конуса дорівнює .

6). Твірна конуса дорівнює .

7). Діаметр меншої основи не може дорівнювати твірній конуса при будь-якому .

8). Діаметр меншої основи може дорівнювати твірній конуса.

Варіант 3

1. Дано зрізаний конус з віссю OO₁, у якого AA₁B₁B — осьовий переріз. Виберіть правильне твердження.

1). AA₁B₁B — рівнобічна трапеція.

2). AA₁B₁B —прямокутник.

3). A₁O₁O = 90.

4). A₁O₁O < 90.

5). AA₁ O₁O — прямокутна трапеція.

6). AA₁ O₁O —  рівнобічна трапеція.

7). Відрізок OO₁ дорівнює висоті конуса.

8). Відрізок OO₁ менше висоти конуса.

2. При обертанні прямокутного трикутника навколо одного з катетів отримали прямий круговий конус. Позначте, які з наведених чотирьох тверджень правильні, а які — неправильні.

1). Один з катетів дорівнює радіусу основи конуса.

2).  Катети більше радіуса основи конуса.

3). Кожний з катетів менше твірної.

4). Один з катетів дорівнює твірній.

5). Гіпотенуза прямокутного трикутника дорівнює твірній.

6). Гіпотенуза прямокутного трикутника більша твірної.

7). Якщо a і b катети трикутника, то площа осьового перерізу конуса дорівнює ab.

    8). Якщо a і b катети трикутника, то площа осьового перерізу конуса

          дорівнює 2ab

1). Осьовим перерізом частини, яка є зрізаним конусом, є трапеція.

2). Осьовим перерізом частини, яка є зрізаним конусом, є прямокутник.

3). Радіуси перерізу і основи відносяться як h : H.

4). Радіуси перерізу і основи відносяться як h : (H–h).

5). Якщо , то твірні обох частин рівні.

6). Якщо , то твірні обох частин відносяться як 1:4.

7). Площа перерізу дорівнює .

8). Площа перерізу менше .

1). Основа піраміди —тупокутний трикутник.

2). Основа піраміди — гострокутний трикутник.

3). Бічні ребра піраміди рівні.

4). Бічні ребра піраміди своєю проекцією на площину основи мають радіус кола, вписаного в основу.

5). Основа висоти конуса не належить основі піраміди.

6). Основа висоти конуса належить основі піраміди.

7). Радіус основи конуса менше 10 см.

8). Радіус основи конуса дорівнює 10 см.

Варіант 4

1. Дано прямий круговий конус з віссю OS. ASB — осьовий переріз конуса. Виберіть правильне твердження.

1). AB — діаметр основи конуса.

2). AB — радіус основи конуса.

3). SB > SO.

4). SB  SO.

5). SOA = 90.

6). SOA > 90.

7). AS = SB.

8). AS > SB.

 

2. Прямий круговий зрізаний конус утворили обертанням прямокутної трапеції з гострим кутом  і прилеглою бічною стороною l навколо меншої бічної сторони. Позначте, які з наведених чотирьох тверджень правильні, а які — неправильні.

1). Радіуси основ конуса дорівнюють основам трапеції.

2). Радіуси основ конуса дорівнюють бічним сторонам трапеції.

3). Твірна дорівнює більшій бічній стороні даної трапеції.

4). Твірна дорівнює меншій бічній стороні даної трапеції.

5). Відстань від центра нижньої основи до твірної менше радіуса нижньої основи.

6). Відстань від центра нижньої основи до твірної дорівнює радіусу нижньої основи.

7). Висота конуса дорівнює lsin.

8). Висота конуса дорівнює lcos.

1). Радіуси перерізу і основи даного конуса відносяться як :.

2). Радіуси перерізу і основи даного конуса відносяться як 1 : 2.

3). Висота даного конуса відноситься до висоти отриманого повного конуса  як :  1.

4). Висота даного конуса відноситься до висоти отриманого повного конуса  як 2 :  1.

5). Площина перерізу відстоїть від вершини на .

6). Площина перерізу відстоїть від вершини на .

7). В отриманий зрізаний конус можна вписати правильну n-кутну зрізану піраміду, висота якої дорівнює .

8). В отриманий зрізаний конус можна вписати правильну n-кутну зрізану піраміду, висота якої дорівнює .

1). Осьовий переріз конуса є тупокутним трикутником.

2). Осьовий переріз конуса є гострокутним трикутником.

3). Площа осьового перерізу менша площі даного перерізу.

4). Площа осьового перерізу більша площі даного перерізу.

5). Площа даного перерізу дорівнює

6). Площа даного перерізу дорівнює .

7). Висота конуса дорівнює sin.

8). Висота конуса дорівнює cos.

 

3 ЗБІРНИК ЗАДАЧ

          Академічний рівень

 

1.  а) Знайти бічну поверхню конуса, діаметр основи якого дорівнює 20см,

          а його висота - 24см.
      б) Знайти об’єм конуса,діаметр основи якого 12см, а його твірна -10см.

2.  а) Знайти бічну поверхню конуса,довжина кола основи якого дорівнює

     12см, а його висота - 8см.
б) Знайти об’єм конуса довжина кола основи якого дорівнює 18см, а

      його твірна – 15см.

3.  а) Твірна конуса дорівнює  m  і утворює з площиною основи кут .

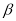      Визначити об’єм.
б) Висота конуса дорівнює  h. Кут між висотою і твірною .

      Визначити об’єм конуса.

4.  а) Твірна конуса дорівнює  m і утворює з висотою кут 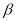. Визначити

      об’єм конуса.
б) Твірна конуса утворює з площиною основи кут . Висота конуса

      дорівнює  h. Визначити бічну поверхню конуса.

 

          Профільний рівень

 

1. а) Через вершину конуса проведено площину під кутом α до площини основи. Ця площина перетинає основу конуса по хорді, яку видно з центра основи під кутом β. Визначити об’єм конуса, якщо центр його основи знаходиться на відстані d від хорди.

б) Через вершину конуса проведено площину, що перетинає його основу по хорді, яку видно з центра основи під кутом β, а з вершини – під кутом α. Відстань від вершини конуса до хорди дорівнює l. Визначити бічну поверхню конуса.

2. а) Через вершину конуса , висота якого дорівнює H, проведено площину під кутом β до площини основи. Ця площина перетинає основу конуса при хорді, що стягує дугу α. Визначити площу перерізу.

б) Через дві твірні конуса, радіус основи якого дорівнює R, проведено площину, що перетинає основу конуса по хорді, яку видно з центра основи під кутом β, а з вершини – під кутом α. Визначити площу перерізу.

3. а) Через вершину конуса проведено площину, що перетинає його основу по хорді, яку видно з центра основи під кутом β, а з вершини – під кутом α. Визначити бічну поверхню конуса, якщо площа перерізу дорівнює S.

б) Через вершину конуса проведено площину, що перетинає його основу по хорді, яка стягує дугу β. Кут при вершині перерізу дорівнює α. Визначити площу перерізу, якщо бічна поверхня конуса дорівнює Q.

4. а) Через вершину конуса проведено площину, що перетинає його основу по хорді, яку видно з вершини під кутом α, а з центра основи – під кутом β. Визначити бічну поверхню конуса, якщо відстань від центра його основи до середини твірної дорівнює d.

б) Через вершину конуса проведено площину під кутом β до площини основи. Ця площина перетинає основу конуса по хорді, яку видно з центра його основи під кутом α. Визначити об’єм конуса, якщо відстань від його вершини до хорди дорівнює l.

5. а) Через вершину конуса проведено площину під кутом α  до площини основи. Ця площина перетинає основу конуса по хорді, яку видно з центра його основи під кутом β. Визначити об’єм конуса, якщо відстань від центра основи до перерізу дорівнює d.

б) Через вершину конуса проведено площину, що перетинає основу по хорді, яка стягує дугу β. Висота конуса утворює з площиною перерізу кут α. Визначити об’єм конуса, якщо відстань від середини його висоти до площини перерізу дорівнює d.

 

4 ЕЛЕКТРОННИЙ РОБОЧИЙ ЗОШИТ

Електронний робочий зошит виконує для здобувача освіти роль маршрутного листа при оволодінні знаннями, уміннями та навичками  з даної теми.

1.  Вхідна діагностика

 Діагностичні завдання призначені для виявлення зони найближчого розвитку здобувача освіти, тобто рівня володіння здобувачем базовими знаннями для вивчення нового матеріалу. Діагностичні листи містять опорні елементи знань і посилання на теоретичний матеріал, до якого здобувач освіти може звернутися у випадку недостатнього володіння складовими навчальної дії, якою належить  оволодіти.

Мета діяльності здобувача освіти: Орієнтація на самостійне розв’язання завдання. Розуміння своєї відповідальності за якість результату навчання.

 

2) Базові знання для вивчення нового матеріалу:

   

 

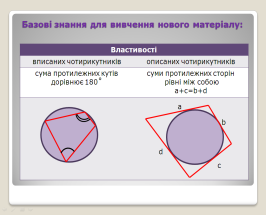
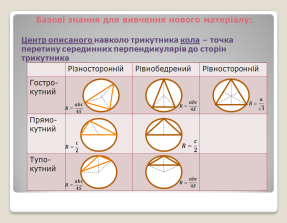
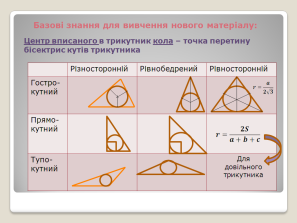
3. Вхідне діагностичне тестування:

  

   

 

 

  

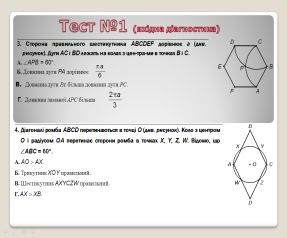
5 ВИСНОВКИ

          Тема посібника на сьогодні є досить актуальною, адже однією з основних цілей вивчення математики є поєднання її з майбутньою професією. Знання, що не пов'язані з практикою, часом забуваються. Якщо ж знання пов'язані з практикою, - вони є більш міцніші, корисніші.

          Електронні засоби навчання, які обрано для вивчення даної теми, використовуються як інформаційно-пізнавальний та інформаційно-контролюючий засіб навчання.

          Презентації мають наочну виразність, є прекрасним дидактичним та мотиваційним засобом, що сприяє кращому запам'ятовуванню навчального матеріалу.

          Проведення актуалізації опорних знань за допомогою тестових завдань сприяє підвищенню інтересу до вивчення геометрії. Різнорівневі задачі сприяють інтелектуальній активності здобувачів освіти, дозволяють ефективно організувати самостійну роботу, сприяють розвитку творчої діяльності здобувачів освіти, вихованню інтересу до вивчення геометрії.

 

 

 

 

 

 

 

 

 

 

6 БІБЛІОГРАФІЧНИЙ ОПИС

1. Математика для техникумов. Геометрия / Под ред. Г.Н.Яковлева.-М.: Наука, 1989. – 174 с.
2. Математика: Підручник / О.М.Афанасьева, Я.С.Бродський, О.Л.Павлов, А.К.Сліпенко. – К.: Вища шк.., 2001. – 447 с.
3. Богомолов Н.В. Практические занятия по математике: Учеб. пособие для техникумов. – 3-е узд., перераб. и доп. – М.: Высш.шк., 1990. – 495 с.
4. Бабенко С.П. Усі уроки геометрії. 10 клас. Академічний рівень.-Х.: Вид. група «Основа», 2010. – 318, [2] с.
5. Математика: Комплексна підготовка до зовнішнього незалежного оцінювання / Уклад.: А.М.Капіносов, Г.І.Білоусова, Г.В.Гап’юк, Л.І.Кондратьєва, О.М.Мартинюк, С.В.Мартинюк, Л.І.Олійник, П.І.Ульшин, О.Й.Чиж. – Тернопіль: Підручники і посібники, 2013. 528с.
6. http://iitzo.gov.ua/biblioteka/elektronni-versiji-zbirnykiv-zavdan-dlya-provedennya-derzhavnoji-pidsumkovoji-atestatsiji-uchniv-4-h-9-h-11-h-klasiv-znz-u-20122013-n-r/ - «Збірник завдань для державної підсумкової атестації з математики. 11 клас»(авт. Глобін О. І., Єргіна О. В., Сидоренко П. Б., Панкратова І. Є.). Повна версія.