Презентація " Кут між площинами. Ортогональна проекція многокутника на площину"
Про матеріал
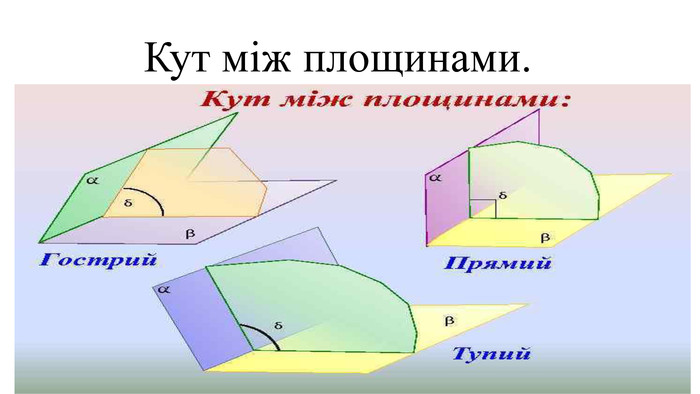
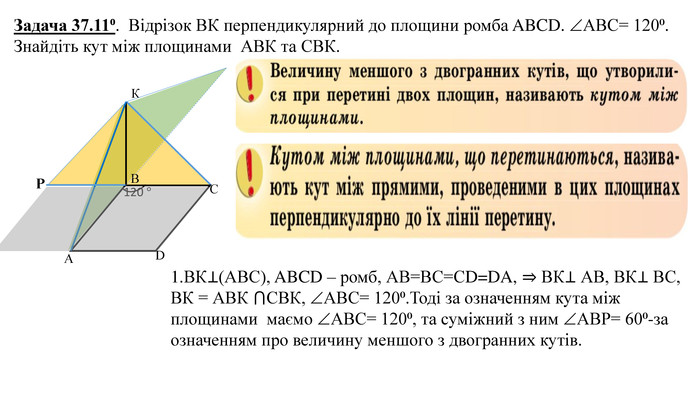
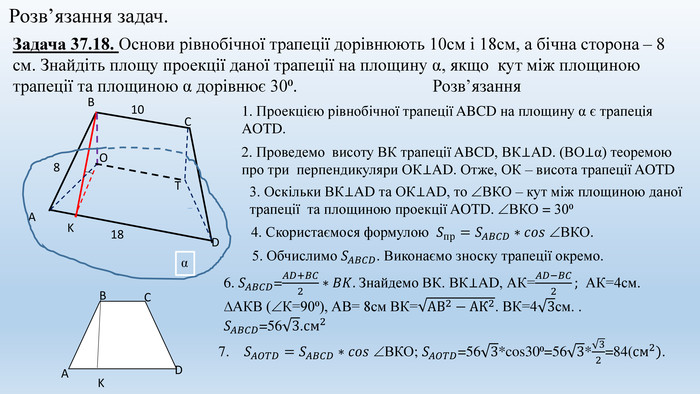
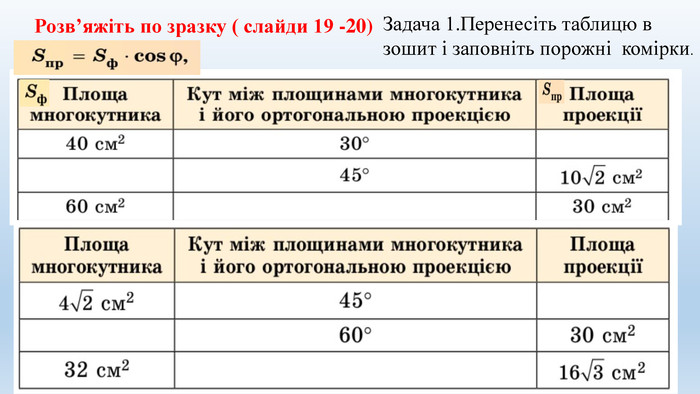
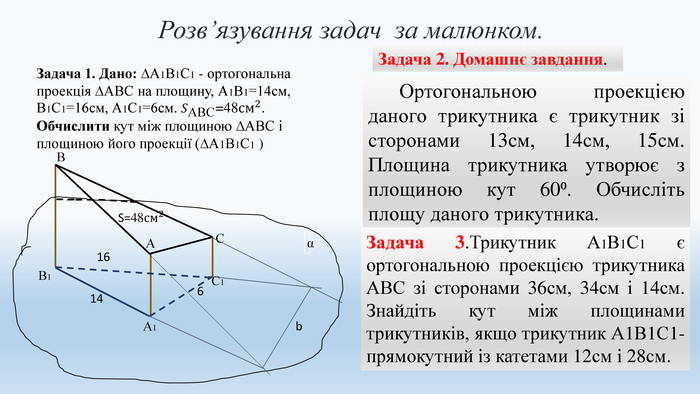
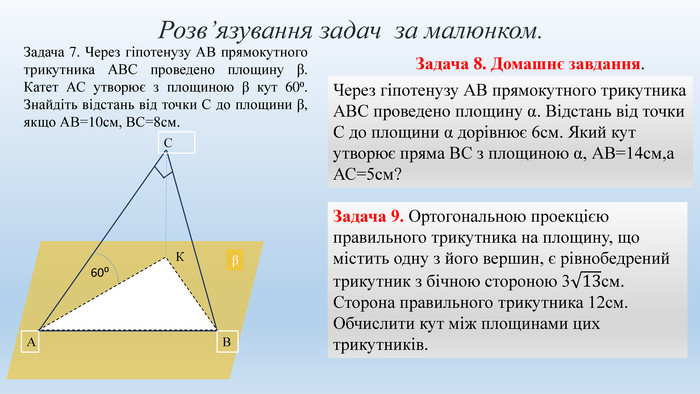
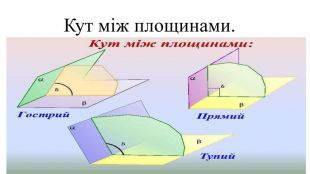
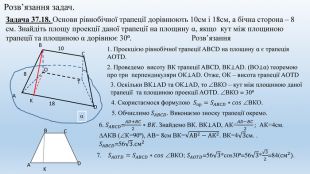
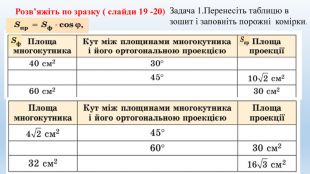
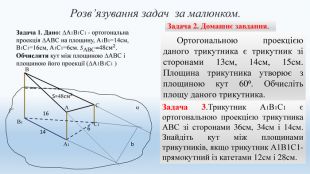
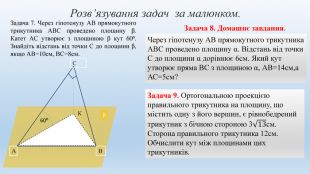
Цю презентацію можна використовувати на уроках геометрії в 10-у класі при вивченні тем "Двогранні кути" та "Ортогональна проекція многокутника на площину". В ній міститься набір задач з розв'язком та запропоновані задачі за готовими малюнками. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку