Урок –змагання з геометрії для 8 класу за темаю: «Розв’язування прямокутних трикутників»

Урок –змагання: «Розв’язування  прямокутних трикутників»

Мета уроку:

• Формувати вміння розв’язувати прямокутні трикутники; навички будувати математичні моделі до задач прикладного змісту;
• розвивати логічне мислення, увагу; вміння застосовувати теоретичний матеріал до розв’язування вправ;
• виховувати наполегливість, активність, самостійність

Девіз уроку: Світ, що нас оточує, - це світ геометрії.

Тож давайте його пізнавати!

Піфагор

Хід уроку:

Учитель. На попередніх уроках ми розглянули прямокутний трикутник, теорему Піфагора та наслідки з неї, розглянули основні типи задач на обчислення елементів прямокутного трикутника.

Прямокутний трикутник – одна з перших геометричних фігур, про властивості якої людство дізналось ще вдавнину.

Задачі про трикутники знаходяться у давньоєгипетських папірусах, давніх індійських книгах.

• Чому ж трикутник цікавив людей з давніх часів?
• А жорсткість трикутника використовували під час будівництва й конструювання.

Сьогодні наша мета – узагальнити й систематизувати набуті знання з теми «Розв’язування прямокутних трикутників» та показати їх практичне застосування.

Урок проведемо у формі змагання( клас ділиться на три команди).

Завдання 1. Історичний екскурс.

1.команда-  Біографія (додаток 1)

2. команда- Наукові досягнення (додаток 2)

3. команда - Чаша Піфагора (додаток 3)

 

Завдання 2. «Мікрофон»

1. Трикутник, у якого є прямий кут  називається…;
2. Сторона прямокутного трикутника, що лежить проти прямого кута, називається...
3. Відношення прилеглого катета до гіпотенузи в прямокутному трикутнику називається …
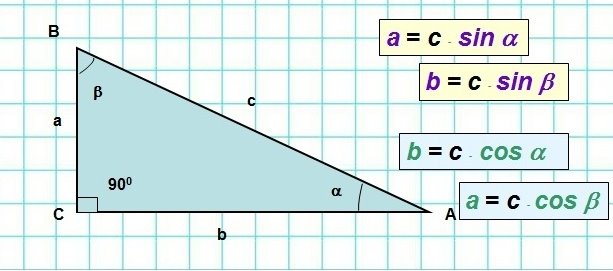
4. Як знайти протилежний катет, через гіпотенузу та синус гострого кута, треба перемножити значення …
5. Тангенсом гострого кута прямокутного трикутника називається …
6. Чому дорівнює катет, який лежить проти кута 30°…
7. Квадрат гіпотенузи дорівнює …
8. Відрізок, що сполучає основу перпендикуляра з основою похилої ...
9. Котангенсом гострого кута прямокутного трикутника називається …

 

Завдання 2. Заповни таблицю

(команди отримують бланк таблиці, перевірка проходить після обміну бланків )

А	00	300	450	600	900	1800
sinA	0				1	0
cosA	1				0	-1
tgA	0	()	1		-	0

 

 

Завдання 3. Розв’яжіть усно

(команди виконують завдання на швидкість)

1.

Знайдіть   sin <А, Знайдіть cos<А, Знайдіть   tg <А, Знайдіть   sin <B,

Знайдіть   tg <B

 

 

 

 

 

 

2.

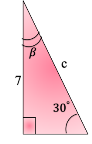
• <β =
• c =
• b =

 

 

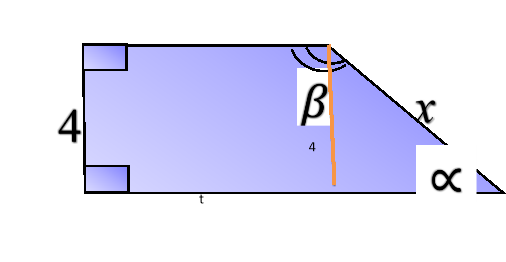
3.

 

• <α =
• <β =
•   x =

 

 

 

Завдання 4. Калейдоскоп

(команди отримують завдання на картках)

1.Обчислити:

2sin30⁰=      ;     2cos30⁰=    ;             6cos60⁰ - tg30⁰=       .

2. Обчислити, скориставшись калькулятором

Sin56⁰=

Cos34⁰=

tg46⁰=

3. Обчислити,  скориставшись таблицями (додатоки1, 2)

Sin26⁰=

Cos64⁰=

tg36⁰=

 

 

 

Завдання 5. Роз’язування прикладних задач

1 .Вузлик

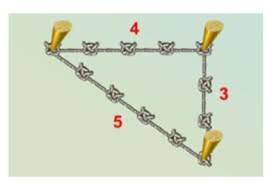(команди з допомогою трьох олівців та вірьовки будують єгипетський трикутник)
 

 

 

 

 

 

 

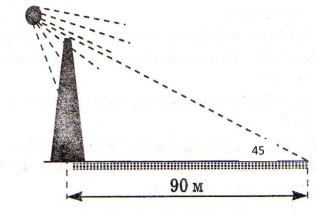2. Визначити висоту вежі (малюнок)

 

 

 

 

 

3 . Задача на знаходження кута

Тінь від антени мобільного зв’язку, висота якої 5 м, дорівнює 2,5 м. Знайдіть висоту сонця над горизонтом (кут а).

 

 

 

4. Задача на знаходження відстані між двома пунктами, які розділені перешкодою.

 

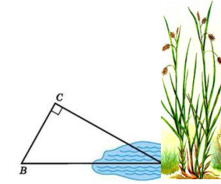
За малюнком знайдіть відстань від об’єкта B до недоступного об’єкта A, якщо ∠C = 90°, BC = 80 м, ∠B = 60°.

 

 

 

Цікава хвилинка

(команди на завершення переглядають відеофільм «Математика та природа»)

 

Підсумок уроку

1. Як ви вважаєте, чому девізом сьогоднішнього уроку ми взяли слова Піфагора?

 

- Чи переконав сьогоднішній урок вас у тому, що прямокутні трикутники займають важливе місце не тільки в геометрії, а й в житті людей різних професій?

 

 

 

Чаша Піфагора

 

Чаша Піфагора (або чаша жадоби) — спеціальна форма чаші для пиття з отвором у дні, яка змушує пити з неї в помірному обсязі. Якщо наповнити чашу тільки до певного рівня, то з неї можна пити, але якщо налити рідини вище цього рівня, то вміст чаші виливається через отвір у дні. Вважається, що Піфагор придумав цю чашу для того, щоби всі раби на острові Самос пили однакову кількість вина і не перевищували своєї норми.

Чаша влаштована таким чином, що в її центрі міститься колона, внизу якої є невеликий прихований отвір, який веде до каналу всередині колони. Канал піднімається до верху колони і потім розвертається й виходить на дно чаші. Чаша Піфагора працює за законом сполучених посудин. Коли рівень рідини в чаші піднімається над найвищою точкою рівня рідини в каналі всередині колони, то гідростатичний тиск створює сифон через отвір і вміст вивільняється через дно. Сучасні унітази функціонують за тим самим принципом, що і чаша Піфагора.

Герон Александрійський використовував чашу Піфагора у своїх гідростатичних приладах.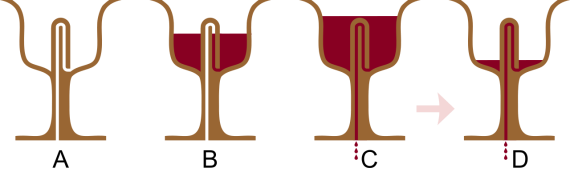

 

 

 

 

 

Наукові досягнення

Піфагор займає почесне місце в історії математики. Він відкрив нову епоху в еволюції наукової думки. Піфагорійці перетворили давно відомі практичні правила в наукові положення, обґрунтовані точними доведеннями. Піфагор увів загальновизнаний тепер дедуктивний метод, суть якого полягає в тому, що, крім невеликої кількості прийнятих без доведень первісних положень, які називаються аксіомами, всі інші твердження математики виводяться логічними міркуваннями.

1.Почувши ім’я Піфагора, ми відразу пригадуємо знамениту теорему: «Сума квадратів катетів дорівнює квадрату гіпотенузи», але вона спочатку була сформульована так: У прямокутному трикутнику площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів, побудованих на катетах.

Нині є понад 150 різних доведень цієї теореми.(Відео)

2. Таблиця Піфагора.

3. Числа Піфагора (піфагорова трійка) складаються з трьох натуральних чисел a, b і c, таких що a² + b² = c². Ці числа зазвичай записують в такому вигляді (a, b, c), і найвідоміший приклад (3, 4, 5).

Примітивними Піфагоровими числами називають взаємно прості a, b й c

 

 

 

 

 

Біографія

Піфаго́р (580 до н. е. — 500 до н. е.) — давньогрецький філософ, релігійний та політичний діяч, засновник піфагореїзм став легендою і джерелом дискусій уже в стародавні часи. У 306 р. до н.е. йому, як найрозумнішому з греків, поставили пам’ятник в римському форумі.

Історію життя Піфагора важко відокремити від легенд, що представляють його як досконалого і величного мудреця посвяченого в усі таїнства греків і варварів. Ще Геродот називав його «найбільшим еллінським мудрецем».

Народився Піфагор острові Самосі, біля узбережжя Малої Азії. Його батько Мнесарх із знатного, але збіднілого роду, був каменерізом.

Батько дав Піфагору добру освіту, навчаючи його в найзнаменитіших учителів того часу. Багато хто вважав, що він — син бога Аполлона. За словами Ямвліха, «набираючи сили й від такої репутації, і від виховання з дитинства, і від богоподібної зовнішності, він ще більше прагнув бути гідним цих чеснот». Після смерті батька Піфагор вирушає до Мілета, де його вчителями були Ферекід, Анаксимандр і Фалес. Саме за порадою Фалеса Піфагор, у віці 20 років, їде до Єгипту, де жив близько 22 років і витримав немало випробувань, перш ніж жерці Мемфіса і Діосполіса відкрили йому «дивовижне чергування чисел, хитромудрі правила геометрії, науку про зорі, медицину». До вавилонських магів і халдеїв він потрапив проти своєї волі —— як полонений перського царя Камбіза, який завоював на той час Єгипет. Там мандрівник прожив 12 років і вивчив у халдеїв релігійні таїнства та математику.

 Доля Піфагора, як і його школи в Кротоні, трагічна. Один із впливових людей Кротона, Кілон, претендував на дружбу Піфагора. Коли його не прийняли до братства через важкий і владний характер, він став його ворогом і організував змову проти піфагорійців. Прихильники Кілона підпалили дім, де збирались піфагорійці. Чи був там Піфагор, точно не відомо, але, за переказами, врятуватися вдалось лише двом: Архіппу та Лісиду. За іншою версією, Піфагор, втікши від заколотників, загинув у Метапонті, у святилищі муз, де залишався без їжі 40 днів

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Підготувала

 вчитель математики

Барбаш О.Ф.