Методична розробка на тему: «Використання інтерактивних технологій при вивченні показникових рівняння»

Про матеріал

Методична розробка на тему: «Використання інтерактивних технологій при вивченні показникових рівняння» допоможе викладачу у підготовці до уроку. Пояснення і демонстрація самі по собі ніколи не дають справжніх стійких знань. Цього можна досягти лише за допомогою інтерактивного навчання. Сутність інтерактивного навчання полягає в тому, що викладач організує пізнавально-навчальну діяльність учня таким чином, що він самостійно розв'язує певні ситуації, проблеми, спираючись на свої потенційні можливості і вже набуті знання у процесі взаємодії «учень — інформація», «учень - ситуація», «учень - знання», «учень - проблема», «учень — учень», «учень — група» тощо. Слід підкреслити, що основні функції інтерактивного навчання — пізнавально-навчальна і корекційна - рівно значущі.

Перегляд файлу

Державний навчальний заклад

«Полтавське вище міжрегіональне професійне училище»

Методична розробка

на тему:

«Використання інтерактивних технологій при вивченні показникових рівняння»

30a36f3bdeac

Розробила викладач:

Заєць В.М.

Полтава 2022

Процес навчання — це не автоматичне «вкладання» навчального матеріалу в голову учня. Цей процес потребує напруженої розумової праці, власної активності дитини в ньому.

Пояснення і демонстрація самі по собі ніколи не дають справжніх стійких знань. Цього можна досягти лише за допомогою інтерактивного навчання.

Сутність інтерактивного навчання полягає в тому, що вчитель організує пізнавально-навчальну діяльність учня таким чином, що він самостійно розв'язує певні ситуації, проблеми, спираючись на свої потенційні можливості і вже набуті знання у процесі взаємодії «учень — інформація», «учень - ситуація», «учень - знання», «учень - проблема», «учень — учень», «учень — група» тощо.

Слід підкреслити, що основні функції інтерактивного навчання — пізнавально-навчальна і корекційна - рівнозначущі. Орієнтація на одну з них або зменшення питомої ваги тієї чи іншої приводить до знецінювання цього методу і викликає розчарування в учителів, так як не дає очікуваних результатів. Важливим є і те, що захопленість формою без дотримання дидактичних умов реалізації методу теж не дає результати?.

Сутність пізнавально-навчальної функції полягає у вихованні схильностей до роздумів. Це риса характеру, яка проявляється перш за все, коли завдання потребує не миттєвої (вивченої) відповіді на задане питання,— інтерактивне завдання потребує зібратися з думками, перш ніж відповідати. По-друге, завдання повинно спонукати учня звертатися до різних джерел інформації під час пошуку відповіді на питання. І по-третє, формування відповіді потребує висловлення не тільки своєї думки (я так думаю) а й аргументації її (чому я так думаю).

Беручи за основу саму сутність «ін» — «звернення до себе», в інтерактивному навчанні важливішим виступає метод педагогічного впливу (супроводу) на пізнавально-навчальну діяльність дитини, за рахунок завдань, що потребують власних зусиль, самостійної діяльності, а не форма. У методі основним постає характер завдань, а формою лише визначаються зовнішні прояви спілкування, висловлення досягнутого, можливості групового, колективного обговорення створеного продукту, сформованої думки, доведення точки зору тощо.

Залежно від охопленості учнів, усі інтерактивні технології навчання

поділяють на такі групи:

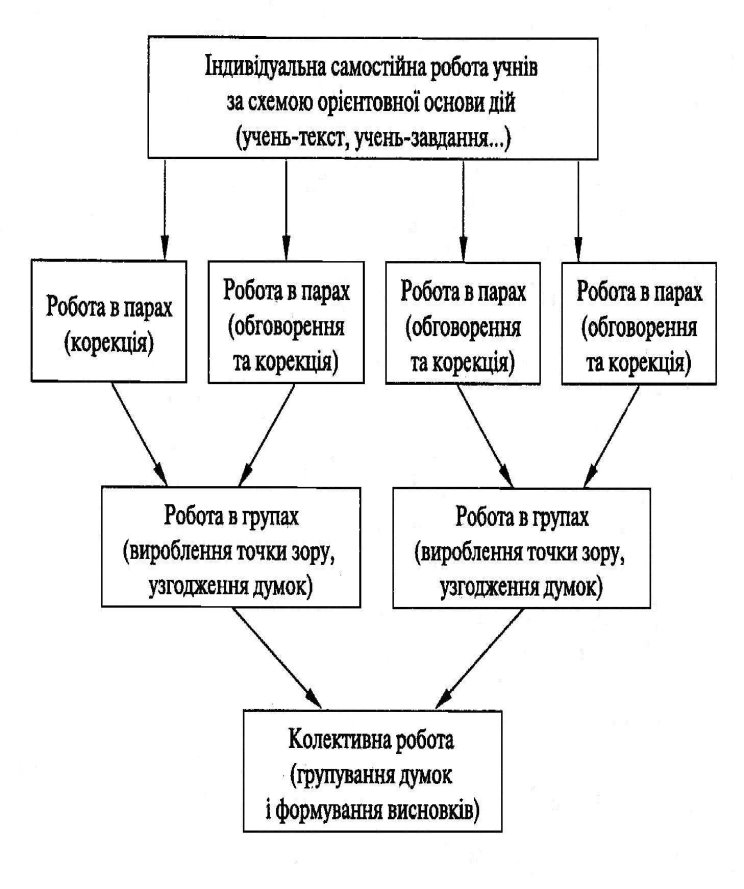
- парну (робота учня в парі з учнем, учителем тощо);

- фронтальну (учитель навчає одночасно групу учнів або увесь клас);

- групову або кооперативну (усі учні активно навчають один одного);

- індивідуальну (самостійну) роботу учня.

Але ми повинні пам'ятати, що не форма є визначальною в інтерактивному навчанні, а методи педагогічного впливу на пізнавально-навчальну діяльність учнів, на розвиток їх мислення, пізнання власних нахилів і здібностей.

За використання кожної з цих груп навчання дидактичні умови мають свої особливості, залежно від поставленої мети.

Наприклад, груповій формі організації інтерактивного навчання повинні передувати індивідуальні інтерактивні підготовчі завдання, а робота в групі — обов'язково наявність спільної мети. Продукт індивідуальної праці використовується за роботи в групі для внесення коректив, змістовного поповнення, уточнення, вироблення спільної думки, формування висновків тощо.

Схематично це може бути відображено таким чином:

$C:\Documents and Settings\Иришка\Мои документы\img003.jpg$

Тема: Розв'язування показникових рівнянь.

Мета:

Освітня :формувати навички та вміння розпізнавати показникові рівняння різних видів та виконувати дії відповідно до вивчених схем для розв’язування цих рівнянь; відпрацьовувати навички розв’язування найпростіших показникових рівнянь та рівнянь , що зводяться до найпростіших; виконувати перетворення виразів, що містять степінь з раціональним показником;

Розвиваюча: розвивати уважність, обчислювальні навички;

Виховна: виховувати пізнавальний інтерес, культуру записів та мовлення.

Тип уроку: засвоєння нових знань.

Обладнання:

- таблиця-ключ,

- правила проведення інтерактивних вправ «Мікрофон» та «Незакінчені речення» (пам'ятка).

Епіграф: слова угорського математика «Якщо Ви бажаєте навчитися плавати , сміло ступайте у воду; якщо ж бажаєте навчитись розв’язувати задачі – розв’язуйте їх» Д. Пойа.

План уроку :

№ з/п	Назва етапу уроку	Час, хв	Методи та прийоми
1	Організаційний момент	2	Звернення до класу
2	Перевірка домашнього завдання	8	1. З усним коментарем. 2. Робота біля дошки.
3	Актуалізація опорних знань	3	«Мікрофон»
4	Розв’язування вправ	30	1.Колективне розв’язу-вання з коментарем. 2.«Повторне відкриття». 3.Навчальна самостійна робота.
5	Підведення підсумків уроку	3	Бліц – опитування
6	Домашнє завдання	1

Хід уроку:

1.Організаційний момент ( 2 хв.)

Привітання;
Відмітити відсутніх;
Перевірка готовності до уроку;
Повідомлення мети та завдань уроку.

2. Перевірка домашнього завдання ( 8 хв.)

№17.2(10,12) та №17.4(3,4) з усним коментарем;

№17.8(3) і №17.10 (1) два учні розв’язують біля дошки.

№ 17.2( 10, 12)

10) =; 12) =

5() =2(); 4(5-3х) = -3(5х-6)

3х -10=12 -3х; 20-12х=-15х+18

6х=22 3х=-2

Х= =3 х= -

№ 17.4( 3,4)

3) =347 4) 3=52

(+4) =347 ( - 3) =52

=1 =52:13

Х-1=0 =4

Х=1 х-2=1

Х=3

№ 17.8 (3)

=·

Х-1=5х+1

-4х=2

Х=-

№ 17.10 (1)

+ +=31

=31

Х-1=0

Х=1

3. Актуалізація опорних знань ( 3 хв.)

Технологія «Мікрофон»

Учитель ставить запитання до учнів. Учням запропоновано певний предмет (ручка, олівець), що виконуватиме роль мікрофона. Діти передають його один одному, про черзі беручи слово. Відповідає тільки той, у кого уявний мікрофон

*) пропонуються до розгляду презентації:

Подайте у вигляді степеня з основою 2:

4^х ; 32 ; 0,5 ; 0,25^2х ; 16^2х ; 8^2х+3 .

У даних виразах винести спільний множник за дужки :

2^х+1 +2^х ; 2^х-1 + 2^х ; 2^х+2 – 2^х-2 .

Розв’яжіть рівняння:

а) 8^2х+1=4; б) 27^3х -81=0; в) .

4.Розвязування вправ ( 30 хв.)

Учням пропонується колективно розв’язати рівняння та прокоментувати етапи розв’язання:

2^х-1+2^х+2=36;
=9;
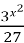=9^х ;

Рівняння 4)-6) учням не знайомі, таким чином виникла проблема !

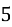^2х+4·5^х -5=0;

Враховуючи, що ^2х=² , вводимо заміну , >0

+4-5=0, тоді або

Повертаємось до заміни , , тобто х=0

Відповідь.х=0

^х + 3·6^х - 4·9^х =0;

Зведемо всі степені до основ 2 і 3:

+ 3 - 4=0 ( маємо однорідне рівняння , у всіх членів однаковий сумарний степінь 2х). Для його розв’язання поділимо обидві частини на .

+ 3 - 4=0, заміна =t , t

t =1, або t=-4- зайвий корінь,

х=0

Відповідь. х=0 .

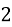^х=1-х; побудувати графіки функцій у=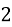^х та у=1-х в одній системі координат.

Відповідь. Х=0.

*) до кожного з рівнянь 4)-6) пропонується презентація з етапами розв’язання.

Давньогрецька мудрість стверджує «Не можна навчитись математиці спостерігаючи, як це робить сусід» . І ми не будемо цього робити, а будемо працювати самостійно .

*) клас ділиться на два варіанти , кожному варіанту пропонуються розв’язати подібні вправи з подальшою взаємоперевіркою:

Варіант 1 Варіант 2

№ 17.5 (1) № 17.5 (3)

-6· +8=0 --20=0

-6t+8=0 -t-20=0

=4, t=2 =-4 – зайвий , t=5

Відповідь. Х=1

Відповідь. або , x=1

№ 17.17(1) № 17.17(3)

3·-5·+2·=0 7·+3·=4·

+3t-4=0

-5t+2=0 =121

=25-4·3·2=25-24=1 = , t= -1- зайвий

= , t= 1 Відповідь. Х= -1.

, або х=0.

*) в цей час 4 учні розв’язують подібні рівняння з карток біля дошки.

- =2

Часто вивчаючи ту чи іншу математичну тему, ми не завжди свідомо розуміємо для чого це потрібно. Для чого ж вивчається показникові функція та способи розв’язування відповідних показникових рівнянь?

( довідка підготовлена учнем )

5. Підведення підсумків уроку ( 3 хв.)

*) Бліц – опитування ( учням пропонується відповісти або «так» , або «ні» ) :

^{1.Чи є спадною функція}