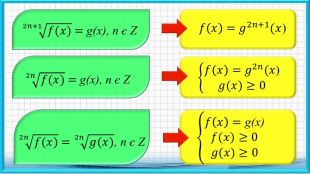
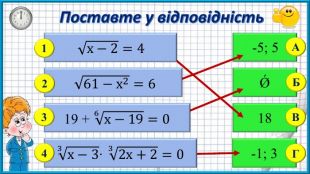
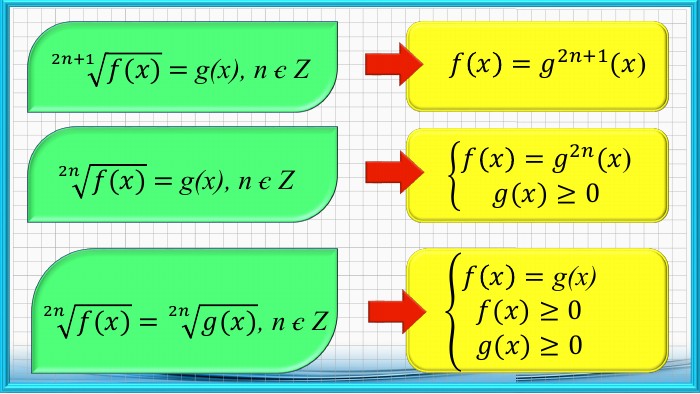
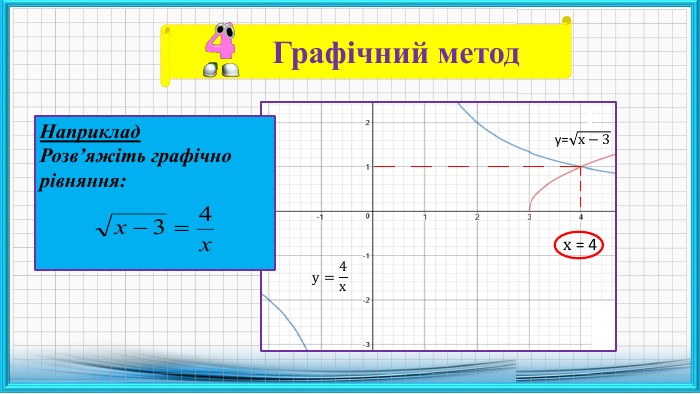
Презентаційний матеріал до заняття на тему: "Розв'язування ірраціональних рівнянь."
Про матеріал
Презентаційний матеріал до заняття на тему: "Розв'язування ірраціональних рівнянь." Презентаційний матеріал до заняття на тему: "Розв'язування ірраціональних рівнянь." Мета: ознайомити з методами розв’язування ірраціональних рівнянь; сформувати уміння розв’язувати ірраціональні рівняння різними методами; провести корекцію знань раніше вивченого матеріалу засвоєння нового. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку






















![Готуємось до ЗНОЗнайдіть область допустимих значень 5−х+х+1=2. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГДR(- ∞; - 1][5; + ∞)(- 1; 5)[- 1; 5] 2. Якому з проміжків належить корінь рівняння 32х=−3. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД−30;−20−20;−10−10;00;1010;20{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД Готуємось до ЗНОЗнайдіть область допустимих значень 5−х+х+1=2. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГДR(- ∞; - 1][5; + ∞)(- 1; 5)[- 1; 5] 2. Якому з проміжків належить корінь рівняння 32х=−3. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД−30;−20−20;−10−10;00;1010;20{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД](/uploads/files/833627/331796/373079_images/24.jpg)



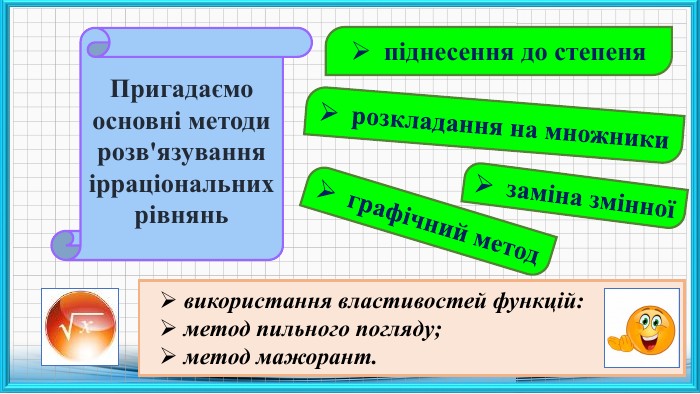
![Завдання додому:.1. [3] - §2, пит. 1-4.2. Розв’язати завдання № 4,6. 3. Творче завдання (проєкт): використання властивостей функцій: метод пильного погляду; метод мажорант. Завдання додому:.1. [3] - §2, пит. 1-4.2. Розв’язати завдання № 4,6. 3. Творче завдання (проєкт): використання властивостей функцій: метод пильного погляду; метод мажорант.](/uploads/files/833627/331796/373079_images/30.jpg)