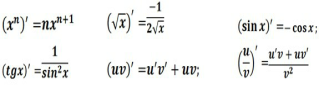Похідна та її застосування

Про матеріал

Тема. Похідна та її застосування Цілі уроку: Освітня компетентність: узагальнити та систематизувати знання та вміння учнів з теми, удосконалити вміння та навички учнів розв’язувати задачі на застосування похідної, продовжити підготовку до зовнішнього незалежного тестування. Розвиваюча компетентність: розвивати пізнавальний інтерес, навички роботи з тестами, логічне мислення. Виховна компетентність: виховувати працьовитість, зібраність, організованість, старанність, відповідальність та вимогливість до себе. Тип уроку: удосконалення знань, умінь та навичок Форма роботи: колективно-групова Наочність: підручник, таблиці, картки з тестами, рисунки з графіками функцій Обладнання: ПК комп’ютерний клас, презентація, таблиця похідних.

Перегляд файлу

УРОК З АЛГЕБРИ, 10 КЛАС

Тема. Похідна та її застосування

Цілі уроку:

Освітня компетентність: узагальнити та систематизувати знання та вміння учнів з теми, удосконалити вміння та навички учнів розв’язувати задачі на застосування похідної, продовжити підготовку до зовнішнього незалежного тестування.

Розвиваюча компетентність: розвивати пізнавальний інтерес, навички роботи з тестами, логічне мислення.

Виховна компетентність: виховувати працьовитість, зібраність, організованість, старанність, відповідальність та вимогливість до себе.

Тип уроку: удосконалення знань, умінь та навичок

Форма роботи: колективно-групова

Наочність: підручник, таблиці, картки з тестами, рисунки з графіками функцій

Обладнання: ПК комп’ютерний клас, презентація, таблиця похідних.

СТРУКТУРА УРОКУ

І. Організаційна частина.

Привітання, перевірка готовності до уроку.

Налаштування на робочу обстановку

Рефлексія (Анаграма настрою)

«Недостатньо лише мати гарний розум,

головне – це добре застосовувати його»

Р. Декарт

ІІ. Мотивація навчальної діяльності. Оголошення теми та завдань уроку.

На попередніх уроках ви засвоїли одне із фундаментальних понять алгебри та початків аналізу – похідну. ЇЇ появі ми завдячуємо таким вченим, як П.Ферма, І.Ньютон, Г.Лейбніц, Ж.Лагранж.

Поняття похідної широко застосовується у механіці, військовій справі, медицині, космонавтиці, фізиці, астрономії. Тому і приділяється така увага цьому поняттю.

ІІІ. Актуалізація опорних знань учнів "ПОВТОРИ"," ЗОРІЄНТУЙСЯ "

інтерактивні вправи: колективна робота «Теоретичний бліц-турнір»,

прийом «Знайди помилку», прийом «Чи правильно, що…», «Знайди пару».

ІV. Повідомлення теми, мети і завдань уроку "ВИВЧИ"

Компетентності учнів (мета)

Я ЗНАТИМУ (Пригадайте)___

Я ВМІТИМУ (Створіть)_____

Я МОГТИМУ (Пам‘ятайте)_____

V. Застосування вмінь та навичок "ВІДТВОРИ" "ЗАПАМ‘ЯТАЙ"

Робота по групах

Інтерактивні вправи

VI. Домашнє завдання "ДОСЛІДЖУЙ ВДОМА"

VII. Підсумок уроку

Карта уроку

ІІІ. ✍ ПОВТОРИ

Колективна робота

Теоретичний бліц-турнір

Група вибирає поняття на дошці і відразу відповідають. Неправильні відповіді виправляють самі учні (і лише за необхідності – вчитель). За правильну відповідь учні виставляють у лист оцінювання кількість набраних балів.

Для учнів зі слабкими знаннями використовується прийом «Незакінчене речення» .

1. Дати означення похідної?	Число, яке дорівнює границі відношення приросту функції до відповідного приросту аргументу за умови, що приріст аргументу прямує до нуля
2. Що таке похідна з механічної точки зору?	S`(t) = V(t); V`(t)=а(t)
3. В чому полягає геометричний зміст похідної. Рівняння дотичної	Якщо функція в деякій точці х_о має похідну, то в цій точці визначено дотичну до графіка функції, при чому її кутовий коефіцієнт дорівнює f`(x₀). Рівняння дотичної y= f^/(x₀)(x-x₀) + f(x₀)
4. Сформулюйте правила диференціювання
5. Ознака зростання функції	Якщо для всіх x з деякого проміжку f`(x) > 0 то функція зростає на цьому проміжку
6. Ознака спадання функції	Якщо для всіх x з деякого проміжку f`(x) < 0 то функція спадає на цьому проміжки
7. Назвіть ознаку точки максимуму функції	Якщо при переході через точку x₀ похідна змінює знак з плюса на мінус, то x₀ – точка максимуму
8. Ознака точки мінімуму функції	Якщо при переході через точку x₀ похідна змінює знак з мінуса на плюс, то x₀ – точка мінімуму
9. Які точки можуть бути екстремальними?	Якщо точка x₀ є точкою екстремуму функцій то f`(x) = 0 або f не є диференційованою в цій точці її називають критичною.
10. Назвіть етапи алгоритму дослідження функції для побудови її графіка

ЗОРІЄНТУЙСЯ

Прийом «Знайди помилку»

(1 учень біля дошки):

Прийом «Чи правильно, що…»

Функція зростає на [-7;2) і (2;8] значить вона зростає на [-7;8] (Ні)
Критична точка є точкою екстремуму. (Ні)
Точка екстремуму є критичною (Так)
Точки на графіку x₁=1, x₂=-1, x₃ = 2 є точками максимуму. (Ні)

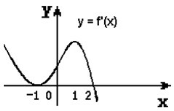
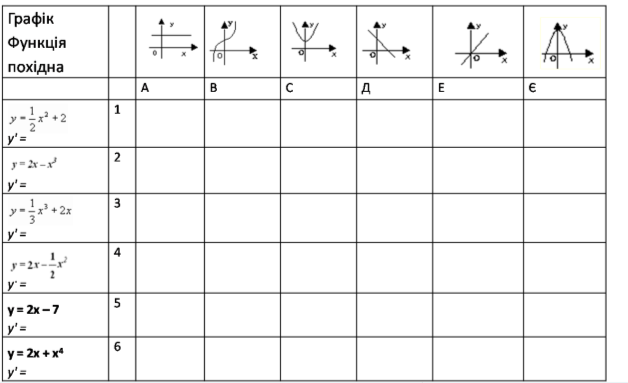
Знайди пару

Знайти похідну функції та відповідний до неї графік.

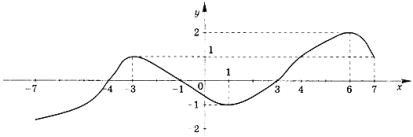
Створити логічну пару: функція+похідна+графік.

ОБРОБИ ІНФОРМАЦІЮ

На рисунку зображено графік функції f(х), визначеної на відрізку [-7;7]. Скільки нулів матиме функція f^/(х) на проміжку (-7;7)?

ІV. ВИВЧИ

Тема уроку.

Похідна та її застосування

Компетентності учнів на уроці (цілі)

Я знатиму (освітня)

розв’язувати задачі на застосування похідної

Я вмітиму (розвиваюча)

використовувати теоретичні знання з теми

при розв’язанні практичних задач

Я зможу (виховна)

впевнено себе почувати під час ДПА та ЗНО,

де досить прості в розв’язанні задачі мають

достатньо нестандартний зміст

V. ВІДТВОРИ

Робота в групах

І група. Знайти точки екстремуму функції.

Розв’язання: у'=4х³-4х

4х³-4х=0, х(х²-1)=0, х(х-1)(х+1)=0

Відповідь: х _max=0; х _min=-1;1.

ІІ група. Знайти найбільше та найменше значення функції на проміжку [-3;2] .

Розв’язання:

f(-3)=81-18-3=60

f(-1)=1-2-3=-4

f(0)=-3

f(2)=16-8-3=5

Відповідь: f _max=60; f _min=-4.

ІІІ група. Знайти проміжки зростання та спадання функції

x	(-∞;-1)	-1	(-1; 0)	0	(0; 1)	1	(1;+∞)
*f′ (x)*
*f (x)*

Розв’язання:

x	(-∞;-1)	-1	(-1; 0)	0	(0; 1)	1	(1;+∞)
*f′ (x)*	-		+		-		+
*f (x)*

Відповідь: зростає (-1;0)U(1;+∞)

спадає (-∞;-1)U(0;1)

ІV група. Знайти критичні точки функції

Розв’язання: у'=4х³-4х

4х³-4х=0, х(х²-1)=0, х(х-1)(х+1)=0

х=0, х=1, х=-1

! ЗАПАМ‘ЯТАЙ

Задача. Знайдіть число коренів рівняння -х³+3х-2=а, якщо а (-4; 0).

Ґрунтовні знання з теми “Похідна” допоможуть Вам без проблем розв’язувати будь-які задачі, пов’язані з похідною.

Існують різні способи розв’язування рівнянь з параметрами, один з них – графічний.

Графічний метод розв’язання рівнянь є доцільним, коли рівняння містить функції з різних класів: наприклад, степенева і тригонометрична, степенева і показникові, тощо.

Додатковою ознакою необхідності застосування цього методу є завдання на знаходження кількості коренів рівняння, а не самих коренів.

(Коментоване поетапне повне розв’язування задачі на дошці)

Виконання завдань у форматі ЗНО.

Виконання тестів – надійний шлях до здачі ЗНО

Тести на картках

№ п/п	Запитання	а)	б)	в)	г)
1	Розв’язати рівняння у’=0, якщо у=х²-4х	-2	-4	2	4
2	Знайти критичну точку функції у=2х²-4х	-1	1	0	2
3	Знайти проміжок зростання функції у=х²-2х-3	(-∞; 1)	(1; ∞)	(-1; 1)	(0; ∞)
4	Розв’язати нерівність у’²	(-∞; ∞)	(-∞; 5)	(5; ∞)	(-5; ∞)

VI. ДОСЛІДЖУЙ ВДОМА

Обговорення заробітної плати

Знайти максимум функції.

(Заробітна плата становить 12 тисяч гривень)

VII. ПІДСУМОК УРОКУ

Сьогодні на уроці ми…
Найважливішим на уроці для мене було…
Найбільше зацікавило…
Найскладнішим для мене було…
Щоб усунути прогалини в знаннях, я маю…

doc

Завантажити

Зберегти на потім

Додав(-ла)

Кухаревич Варвара

Пов’язані теми

Алгебра, 10 клас, Розробки уроків

Додано

20 лютого 2023

Переглядів

641

Оцінка розробки

Відгуки відсутні