Похідна функції, її геометричний і фізичний зміст

 

Тема : Похідна функції, її геометричний і фізичний зміст.

Мета:

навчальна: формувати предметні (математичні) компетентності:

обчислювальна :

- уміння обчислювати  вирази;

- уміння користуватися математичною термінологією;

- уміння знаходити кут, під яким дотична до графіка функції перетинає вісь абсцис;

- уміння розв’язувати задачі на застосування геометричного і фізичного змісту похідної;

- уміння здійснювати дослідження, аналіз, планування послідовності дій для розв’язання задач.

логічна:

- уміння виконувати логічні вправи.

розвивальна: розвивати ключові компетентності:

  - математична компетентність:  уміння застосовувати математичні методи для вирішення прикладних завдань, усвідомлення ролі математичних знань і навичок в особистому та суспільному житті людини;

-  спілкування державною  мовою: висловлювати й тлумачити поняття й думки мовою навчання;

- інноваційність: відкритість до нових ідей, ініціювання змін у близькому середовищі;

- інформаційно-цифрова компетентність: використання засобів ІКТ в навчанні;

- уміння вчитися впродовж життя: здатність до пошуку та засвоєння нових знань , аргументувати,доводити правильність тверджень.

- соціальна та громадянська компетентності: уміння працювати з іншими на результат,уміння висловлювати свою думку, слухати і чути інших

виховна:

  виховувати зацікавленість до вивчення точних наук; виховувати звичку ; старанність, акуратність оформлювати конспект,  товариськість, самостійність, культуру математичної мови;

  - виховувати дбайливе ставлення до навколишнього середовища. показувати учням, наскільки ця тема  важлива при розв’язанні задач

Наскрізні змістовні лінії:

- Громадянська відповідальність: колективна робота в групі;

- Екологічна безпека : збереження природного середовища, готовність брати участь у розв’язанні питань довкілля та розвитку суспільства;

- Здоров’я та безпека : дбайливе ставлення до власного здоров’я.

Тип уроку : комбінований урок ( урок перевірки раніше засвоєного матеріалу й засвоєння нових знань).

Міжпредметні зв’язки: математика, інформатика, фізика, історія

Обладнання: підручник, картки для  роботи в групі, вебсервіс Google Classroom ,Google Meet (засіб для відеоконференцій) ,  цифрова інтерактивна дошка Google Jamboard , сервіс  SMART Notebook.

Форми роботи : колективна, індивідуальна, групова.

Технології: інтерактивна, технологія «Створення ситуації успіху», ігрова, технологія розвитку критичного мислення.

Методи: акмеологічні: «Повір у себе»,   «Констатація успіху», метод порівнювання, метод дослідів.

Техніки позитивного звернення до учнів: комбінація технік надихання-схвалення, комбінація технік спонукання-схвалення

Хід уроку:

 

I. ОРІЄНТАЦІЯ, МОТИВАЦІЯ ДІЯЛЬНОСТІ.

 

Техніка надихання 

 

Учитель

Шановні здобувачі освіти, добрий день!

 

• Я хочу вас навчити  зрозуміти   геометричний і фізичний зміст  похідної функції  .  Це не просте завдання, але я вірю, що кожен з вас опанує ці знання.
   
• Я відчуваю, що у Вас  все вийде.
• Я вірю у  Вас.
• Все буде Україна.

 

Знання, вміння, навички, старання.

Інтерактивна вправа «Ланцюжок добрих побажань».

- Побажайте одне одному (ланцюжком) успіхів і цікавих відкриттів  на сьогоднішньому уроці.

- Покажіть за допомогою реакції , який у вас  зараз настрій.

 

II.ЦІЛЕПОКЛАДАННЯ

1. Повідомлення теми, мети, завдань уроку.

Сьогодні на уроці ми будемо продовжувати вивчити похідну функції. Будемо досліджувати її геометричний і фізичний зміст .Вчитися знаходити кутовий коефіцієнт і кут нахилу, під яким дотична до графіка функції перетинає вісь абсцис. розв’язувати задачі на застосування геометричного і фізичного змісту похідної.

 

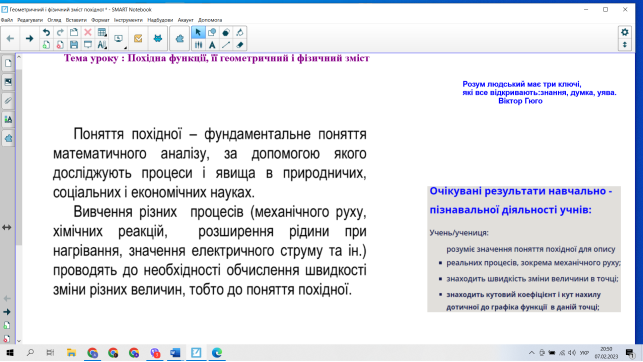
2. Визначення очікуваних результатів.

Отже, діти, чого ви очікуєте від сьогоднішнього уроку?

(Отримати нові знання, щодо розв’язування задач на застосування геометричного і фізичного змісту похідної)

Так, сьогодні ми маємо зробити важливі висновки щодо розуміння значення поняття похідної для опису  реальних процесів ,зокрема механічного руху

Тому, щоб нічого не випустити з поля зору, ви маєте бути дуже уважними, працювати сумлінно, аби зробити для себе нові цікаві відкриття!

3.  Мотивація навчальної діяльності.

Комбінація технік надихання-схвалення (до класу)

• А зараз будь ласка заспокойтся і постарайтеся зрозуміти основну думку.
• Сконцентруйте свою увагу на геометричному та фізичниому змісту похідної функції
• Мені здається, що  ви добре попрацюєте, дасте чудові відповіді.
• Я, відчуваю, що ми будемо спілкуватись дружно і злагоджено, застосовучи математичні методи ,для розуміння геометричного і фізичного змісту похідної функції 

.III. ЦІЛЕРЕАЛІЗАЦІЯ.

1. Усебічна перевірка ступеня раніше засвоєних знань.

1.1. Пригадаємо разом

1. Математичний  аналіз -це?

(Відомий розділ математики, який демонструє  диференціальне й інтегральне обчислення.)

2.  Який вклад внесли Ньютон та  Лейбніц до математичного анвлізу  ?

(  Незалежно Ньютон у Англії Лейбніц у Німеччині, одночасно створили  у XVII столітті математичний  аналіз .)

3. Як вплинуло поява математичного  аналізу на капіталізм  

(Технічна революція в Європі  розпочалася з появи парових машин ,які сприяли удосконаленню технологій  в гідротехніці, мореплавстві, військовій техніці ,а саме застосування геометричного і фізичного змісту похідної  для обчислення швидкості та прискорення   руху транспорту, кулі тощо .Ключовим є визначення швидкості зміни різних фізичних величин.

4. Що є основним у змісті похідної?

(Швидкість зміни функції).

5. Кому належить визначення  термін «похідна»?

 (французькому математик: Луї Лагранж.)

 1.2. Актуалізація вміння застосовувати правила  диференціювання та похідні деяких елементарних функцій

Знайдіть похідну

1) ;  

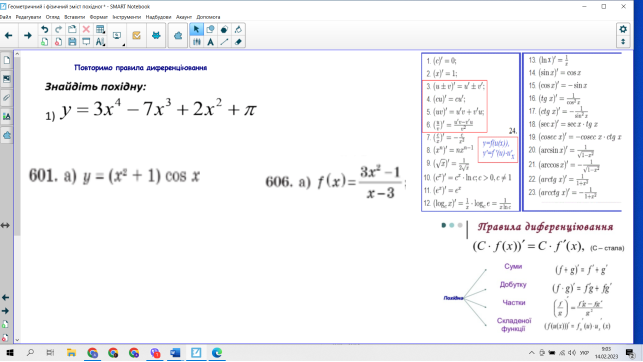 2)у=+    ;

3)у= sinx  cosx;

4)у=5tgx .

                                              Фізкультхвилинка для очей.

 

 

https://www.google.com/search?q=%D1%84%D1%96%D0%B7%D1%85%D0%B2%D0%B8%D0%BB%D0%B8%D0%BD%D0%BA%D0%B0+%D0%B4%D0%BB%D1%8F+%D0%BE%D1%87%D0%B5%D0%B9&rlz=1C1GCEA_enUA1038UA1038&oq=%D0%A4%D1%96%D0%B7%D1%85%D0%B2%D0%B8%D0%BB%D0%B8%D0%BD%D0%BA%D0%B0+%D0%B4%D0%BB%D1%8F+%D0%BE%D1%87%D0%B5%D0%B9.&aqs=chrome.1.69i57j0i22i30l7.16782j0j7&sourceid=chrome&ie=UTF-8#fpstate=ive&vld=cid:944e1fa8,vid:9znAKmoG9tg

 

Здоров’язберігаючі вправи, що сприяють зміцненню ослаблених очних м’язів   ( за відсутності світла ,інтернету)

   Спочатку, як почати вправи, хвилину поморгайте без заплющення та  напруження.

1. Спочатку подивись вгору вздовж осі Оу, потім опусти очі вниз (3 повтори).

2. Змінюй погляд очима ліворуч вздовж осі Ох, потім праворуч (3 повтори).

3. (3 повтори).праворуч-вгору, а потім ліворуч-вниз (3 повтори).

 4.В зворотному напрямку: змінюй погляд очима вгору -праворуч ,а потім вниз-ліворуч(3 повтори).  

 

 

2. Сприйняття  й усвідомлення учнями нового матеріалу.

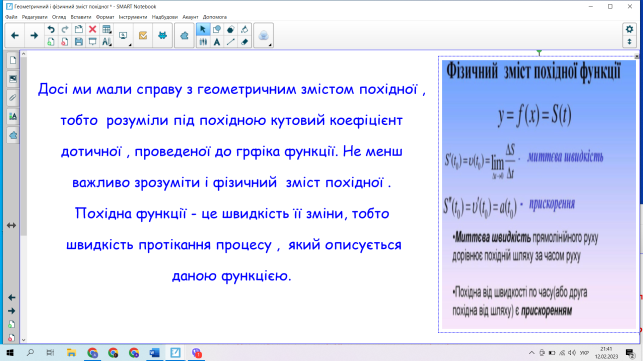
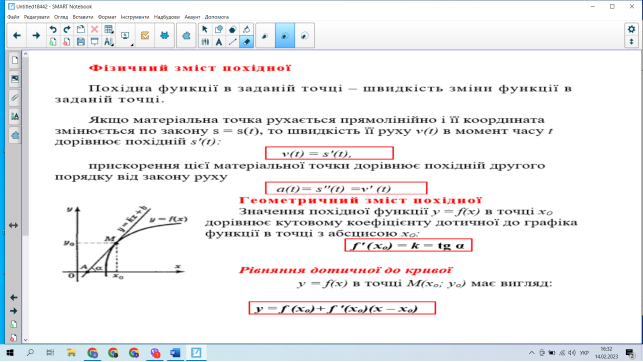
2.1 Формування поняття про  геометричний і фізичний зміст похідної.

-Історична довідка про похідну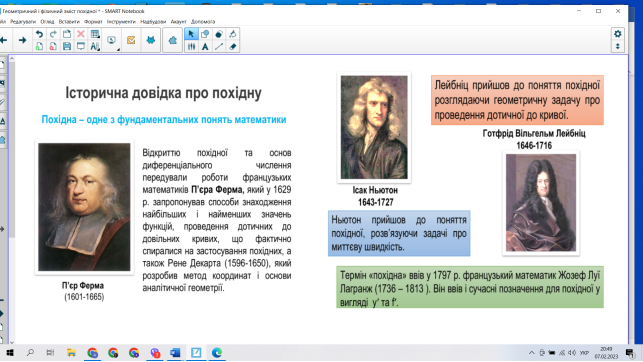

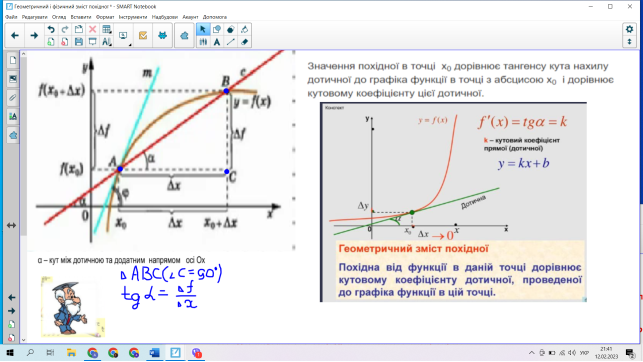
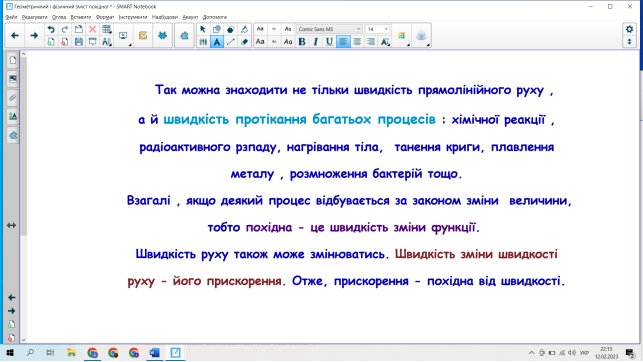
-Поняття похідної з’явилось  як необхідність знаходити кутовий коефіцієнт і кут нахилу, під яким дотична до графіка функції перетинає вісь абсцис ,та визначення миттєвої  швидкості та прискорення тіла в будь – який момент часу при  прямолінійному нерівномірному руху.

 

 

 

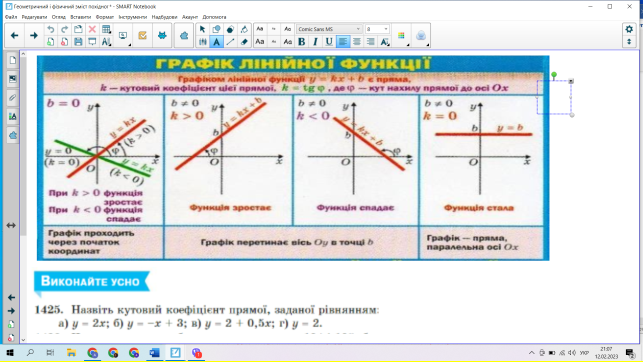
Для розуміння  знаходити кутовий коефіцієнт і кут нахилу, під яким дотична до графіка функції перетинає вісь абсцис пригадаємо лінійну функцію.

 

 

 

 

 

 

 

 

 

 

Фізкультхвилинка.

https://www.youtube.com/watch?v=A80CAAp6l7M&ab_channel=%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%BD%D0%B8%D0%B9%D0%9A%D0%BB%D0%B0%D1%81

 

 

 

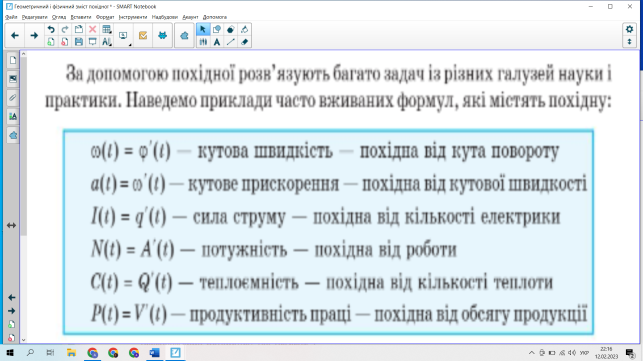
2.2 Формування вміння розв’язувати задачі на застосування геометричного і фізичного змісту похідної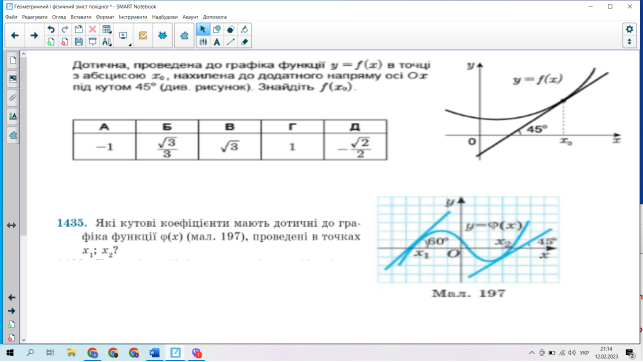

 

 

.

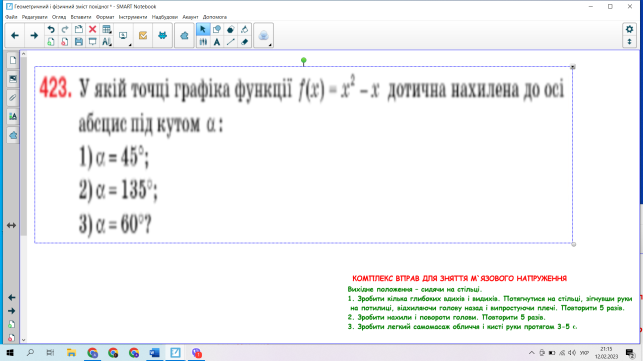
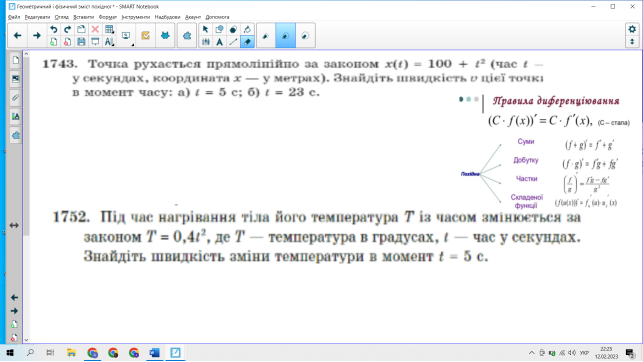
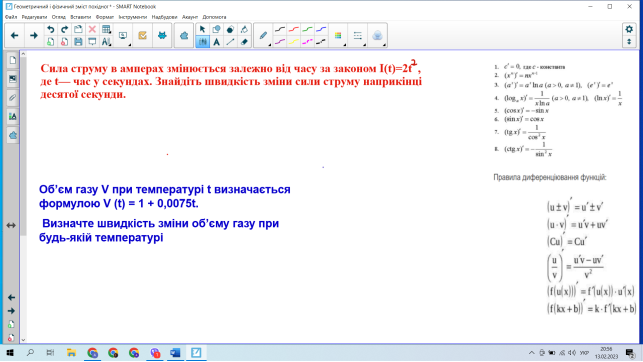
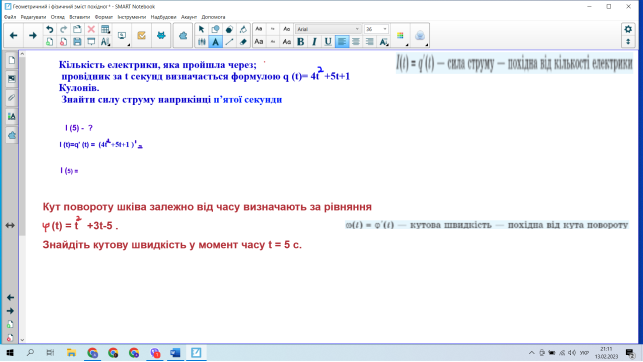
3. Осмислення, первинна перевірка розуміння й корекція засвоєння нових знань.

Робота в групах.. Працювати ,вчитись самостійно  є необхідною умовою в життєдіяльності людини. Щоб досягти успіху в житті необхідно спілкуватись з щирими однодумцями. Тому під час виконання наступної роботи дозволяється здійснювати взаємодопомогу. Протягом виконання завдання застосовуйте  знання з фізики ( формули кінетичної енергії та  другого закону Ньютона), розвивайте думку, уявляйте покрокове  розв’язування

 

Самостійна робота над задачею. До вашої уваги:   завдання а) виконує  група 1 інформатики, завдання б) виконує  група 2 інформатики. Учні розв’язуюють з подальшою самоперевіркою.

 

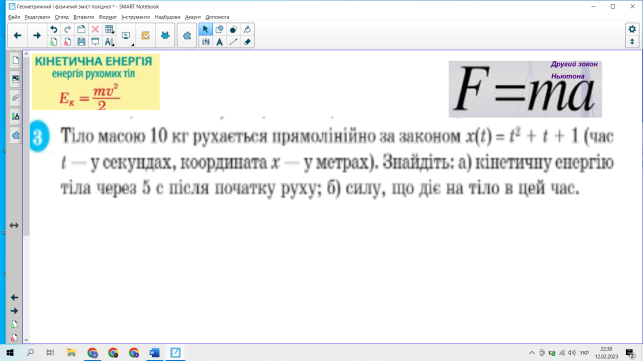
Молодці! Всі правильно виконали завдання.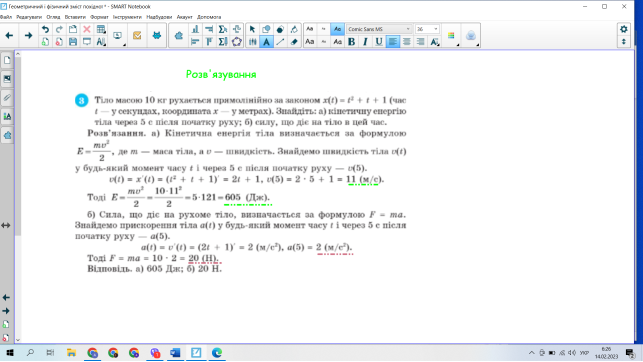

 

 

 

 

4.Підсумок уроку

Отже, ми сьогдні досліджували  геометричний і фізичний зміст похідної. Вчилися знаходити кутовий коефіцієнт і кут нахилу, під яким дотична до графіка функції перетинає вісь абсцис, розв’язувалии задачі на застосування геометричного та фізичного змісту похідної.

 

IV. РЕФЛЕКСИВНО-ОЦІНЮЮЧИЙ

Вправа «Мікрофон»

А тепер закінчи речення:

Сьогодні я навчився…

Найбільше мене зацікавило…

На уроці я дізнався…

Найскладнішим  я відчув…

На наступному уроці я хочу…

Техніка схвалення (до класу)

• Я така задоволена, що ми всі сьогодні так позитивно і злагоджено попрацювали
• Мені приємно про це сказати, що тему урокуви так уважно слухали і тому так добре засвоїли. (до учня)
• Як добре, що ти повірив у свої сили і виконав це завдання.
• Як чудово, що ти не зупинився перед труднощами, а подолав їх.